Rep:Mod:sm17123
The Free Energy and Thermal Expansion of MgO: Introduction
A property of a material can be seen as an average over the different states of the molecules withing the material. For sufficiently small systems an analytical approach can be taken by hand to add all the vibrations of the molecule. This however is impossible for a material with many atoms as the maths becomes more and more complicated. Fortunately, we can use computer modelling to calculate energies and vibrations utilising different computational theories and methods.
In this experiment, the harmonic, quasi-harmonic, and Molecular Dynamic approaches will be used to compute the energies and vibrations of MgO. These results will be used to calculate the free energy of the crystal and the thermal expansion across a range of temperatures to find the thermal expansion coefficient for MgO. This experiment will compare how results vary with the lattice sizes used and also the theory being applied, discussing the origins and limitations of each.
We will be using DLVisualize on Linux to model and view our MgO lattices. The molecular modelling code GULP (General Utility Lattice Program) will be used, which is a program based on force field methods. For these calculations a simple force field for MgO will be used giving the Mg ion a charge of +2e, the O ion -2e with a Buckingham potential operating between the ions to describe the Pauli repulsion and van der Waals energy. This potential is shown below[1]:
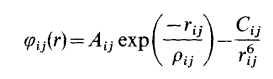
Methodology
Using the Harmonic Approximation
The Harmonic Approximation relies on the basis of the harmonic potential to model interactions between molecules. Vibrations between two molecules are treated as if a spring resides between them, following Hooke's law with a force constant K. The Energy distribution with respect to inter-nuclear distance is therefore seen as parabolic - counter intuitive as when molecules reach a certain separation they dissociate. The Harmonic potential is therefore only valid around a small inter-nuclear distance range, at the bottom of the parabolic curve. Here calculations can be made that can tell us many properties of a system.
For a crystal such as MgO, the vibrations can be counted by understanding that the lattice is formed of many repeating unit cells. MgO forms a face centered cubic cell with eight atoms in each unit. Below shows a lattice made of two unit cells in the x,y and z axis.

If we can work out the properties of one unit we can apply it to our larger lattice to get our desired results.
The Quasi-Harmonic Approximation
When we start to look at thermal expansion, using a simple harmonic potential to classically model this system fails. The equilibrium distance between the magnesium and oxygen atoms become invariant with temperature, meaning the MgO lattice will have no thermal expansion at any temperature. We know this cannot be true, and we can start with the fact that in reality vibrations are not purely harmonic and are in fact anharmonic. When a diatomic increases in nuclear separation, past a certain length the model dissociates. This is not modeled for in the Harmonic Approximation.
As a periodic lattice the anharmonicity that does arise is weak and so we can approximate the thermal expansion with the Quasi-Harmonic Approximation (QHA), a theory based in quantum mechanics.[2] In the QHA the phonon frequencies become volume dependent, and so that for each volume the Harmonic Approximation can be used. The free energy therefore becomes a sum over all the vibrational modes in the crystal, with the accuracy of this calculation increasing with the number of points in the lattice. The Helmoltz Free Energy can be described in the QHA as[3]:

Molecular Dynamics
Molecular dynamics is a different technique used to model systems. Also called 'Ab initio MD' - Latin for 'from the beginning' - it unifies molecular dynamics with electronic structure theory using classical physics.[4]. It takes time averages of the trajectories that the atoms would follow in reality, simulated by Newton's second: law F=ma. MD includes anharmonicity into its calculations which makes this method more accurate at higher temperatures.
Results and Discussion
The Internal Energy of MgO
Every vibration in the unit cell has a corresponding wave-vector k - a value in reciprocal space. Real space and reciprocal space are related by Fourier transforms. We can use k-space to perform analysis on our lattice as it simplifies the equations and is easier to work with than with 3D real space planes and vibrations. The frequency of vibration can be converted to a k value with the following equation:
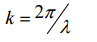
Summing over k can give us the internal energy of a crystal in the following equation[5]:
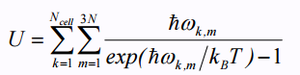
For the 2x2x2 lattice the internal energy was computed using the Harmonic Approximation giving a result of -41.08eV. The output file for this calculation can be found here.
Lattice Vibrations - Computing the Phonons
Phonon Dispersion Curves
In this part of the experiment the vibrational modes for MgO were computed. The vibrational - or phonon - modes are displayed in the following table as dispersion curves. Each value of k was plotted as a continuous graph as a simplified way to display the different frequencies of the phonons.[6] It can be given in the following equation:
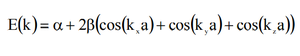
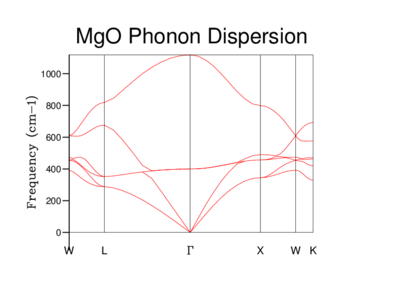
In this computation, phonons were computed at 50 points along this path. More points could be used but the computational costs of the calculation may not necessarily be compensated for in improved accuracy. In the first picture of the 2x2x2 lattice, we can see clearly the lines which converge to the point 'Γ' which is the origin. These curves are called 'acoustic branches' and the upper curves called 'optical branches'.[7] The phonon dispersion's below show the vibrational frequency of each different lattice as a function of k.
 |
|---|
 |
 |
As the grid size increases it is easy to see how the Phonon dispersion becomes more complicated.This is due to the increase of our length 'a' - ie how large our lattice is we are using for the calculations. The Brillouin zone is a defined primitive cell in reciprocal space, and what is used in the calculation. As it is inversely related to real space, when the unit cell length 'a' increases, the Brillouin zone gets smaller. The energy bands have to 'fold' back once or many times to fit into the smaller Brillouin zone.
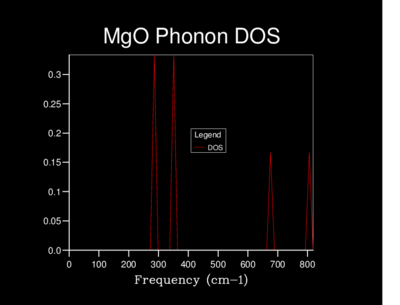
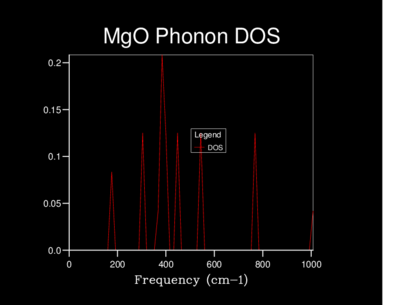
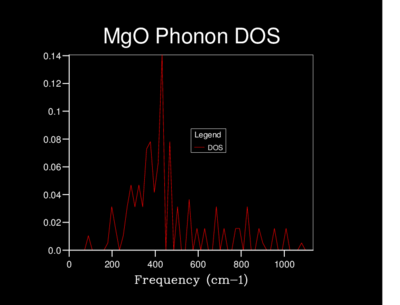
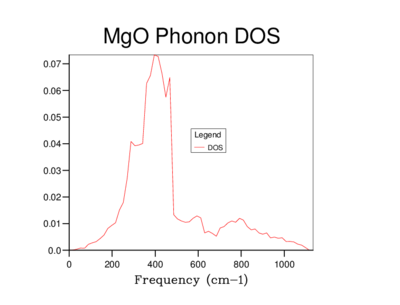
Phonon Density of States
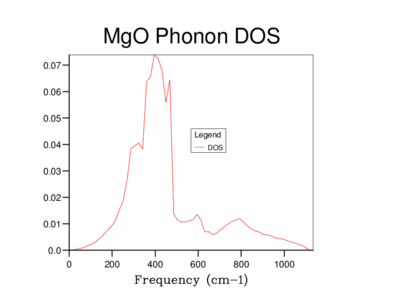
The Density of states (DOS) was also calculated for each grid size. The DOS is the number of allowed vibronic modes at a particular frequency.[8] We can therefore use the DOS to show an 'energy level' diagram for the phonons and see which frequency gives the most vibronic modes in the crystal structure.
In the 1x1x1 DOS we can see from the log file that the k-point used for this data was 0.5. This can also be seen by the graph. The graph first reaches L the first symmetry point which represents the vector (π/a,π/a,π/a). K points are related to lattice points with the following equation:
Where Nxyz are the number of lattice sites in each direction and nxyz are integers up to N, relating to a specific vibronic state. We can therefore see that this relates to the point (0.5,0.5,0.5).
The table below shows the differences in the highest density frequencies produced by the different sized grids as taken from the log files:
| Grid Size | Highest Density Frequency (cm-1 |
|---|---|
| 1x1x1 | 256 and 381 |
| 2x2x2 | 384 |
| 3x3x3 | 408 |
| 4x4x4 | 432 |
| 10x10x10 | 396 |
| 20x20x20 | 396 |
| 30x30x30 | 396 |
From the log files we can see that the most probable vibrational frequency was at 396cm-1. From 10x10x10 the highest density frequency remains the same while the lower grid sizes vary dramatically. The larger size of 20x20x20 is more accurate than 10x10x10 with more information as seen on the graph and at a lower computational cost than the 30x30x30 grid.
The dispersion relation shows the energy of each k value and the DOS shows how many k values have the same Energy. In this way the DOS is proportional to the inverse of the dispersion curves. The flatter the band, the greater the density of states at that energy. Below shows a diagram demonstrating this[9].

We can use the graphs collected from this experiment in a similar comparison to show the relation between the DOS and dispersion curves. Below shows the dispersion and DOS for the 30x30x30 lattice with slight manipulations to achieve the same comparison as above:

Other Calculations
Lithium has a lattice parameter of 3.5Å and so being similar to MgO, 20x20x20 would be a suitable grid size for calculation. CaO has a lattice parameter of 4.8Å and so also being similar we can assume this grid size would be appropriate for calculations.
The grid size would be too big to model a zeolite. A zeolite unit cell has the size of approximately 24.7Å[10], in comparison to the MgO size of 4.2Å is far bigger. The computational cost to do 20x20x20 cells of 24.7Å each would be too high and therefore not feasible. A smaller grid size could be more appropriate.
Calculating the Free Energy in the Quasi-Harmonic Approximation
Computing Free Energies
Below, using the QHA the free energy of different sized lattices was computed. The larger the number of points in the lattice used the more 'expensive' the calculation, meaning that the computation takes more and more time. Therefore there is the need to find a lattice size big enough for suitable accuracy, yet small enough that the cost of the calculation is not too high. The shrinking factors can be changed as before to change the number of points being averaged.
| Grid Size | Total Free Energy (eV) |
|---|---|
| 2x2x2 | -40.926414 |
| 3x3x3 | -40.926432 |
| 4x4x4 | -40.926450 |
| 5x5x5 | -40.926463 |
| 10x10x10 | -40.926480 |
| 20x20x20 | -40.926483 |
| 30x30x30 | -40.926484 |
With the grid size the free energy decreases by minute amounts; the range being 0.07meV, but we can see that smaller grids overestimate the free energy. Ultimately we want a grid that predicts the minimum free energy, but with increasing grid size comes increasing computational cost. The small range between the grids however makes all the grids appropriate for calculations accurate to 1meV, 0.5meV and 0.1meV. It was decided that the 20x20x20 lattice was suitable to model the system further. The energy difference between results from the 20x20x20 and 30x30x30 grids wass 0.001meV, making the 20x20x20 lattice almost the same in terms of result but with substantially less computational cost. Looking at the DOS plots in the previous exercise it can also be seen that between these two grids the change in the shape of the graphs are minimal. Comparing to literature, the results calculated were converted into electron volts per mole per unit cell. This gave -2.46x1025eV/(mole unit cells), comparing to literature approximations of -3.12x1025eV/(mole unit cells)[11] we can see that while the result varies, it is quite similar when we consider the approximations made in the theory. These approximations will be discussed in a later section.
Other Calculations
This 20x20x20 grid would be suitable for a calculation on a similar oxide for example CaO. The radius of a calcium ion is 49pm larger than magnesium (194pm vs 145pm)[12] . The harmonic potential used in these calculations relies on the reduced mass of the two atoms. This can be expressed as: (m1+m2)/(m1xm2). For MgO it is:
For CaO it is:
The difference here is minimal and as Mg and Ca have the same charge as they are in the same group, we would expect the calculation to be an accurate approximation.
A metal lattice such as one made from Li is probably not accurately approximated by this model. Lithium has a body centered cubic lattice unlike MgO's face centered cubic, however both the cells have eight atoms in them. Lithium is however a very light element, and we would expect that a Li-Li bond would have a lower stretching frequency making it stretch further than MgO at higher temperatures.
This lattice could not model zeolite, as zeolite undergoes negative thermal expansion,as when upon heating the structure expands into the pores of its own unit cell and not positively outwards. It therefore shrinks upon heating. [13] This interesting property can be used to make materials with controlled thermal expansion properties such as glass-ceramics which experience no expansion at all.[14]
The Thermal Expansion of MgO
Calculating Free Energies
From the previous investigation the 20x20x20 shrinking parameters for the MgO lattice were deemed suitable enough to undergo further calculations. Using the QHA the structure of MgO was optimised at different temperatures to minimise the free energy. The Free Energy was calculated from 0K-1000K with the lattice constant also being noted at each temperature. Below shows a summary of the results:
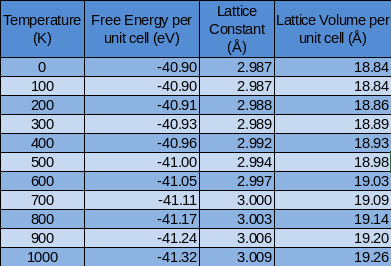
The free energy was plotted against temperature:
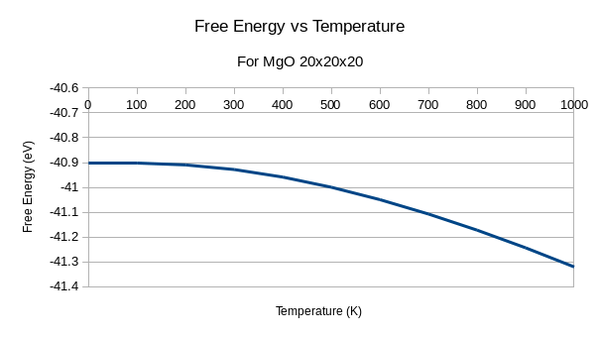
For this graph we can see that the free Energy decreases with increasing temperature. This relates to the equation of free energy:
Therefore as temperature increases there are more ways of arranging the molecule and more ways it vibrates. This is a negative term in the equation so the total free energy decreases.
Thermal Expansion
To find the thermal expansion coefficient the lattice constant was plotted against temperature:
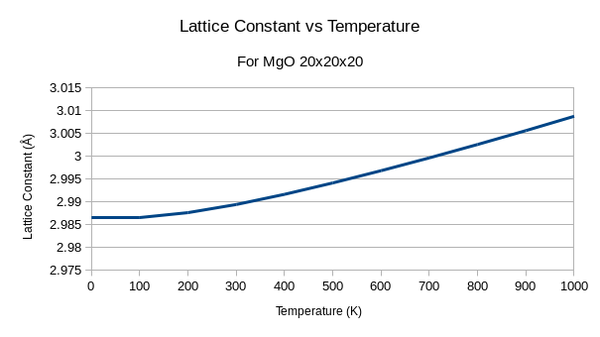
In this graph there is almost no expansion until about 200K where the expansion increases at a linear rate. This shape can be explained by the physical origin of Thermal expansion which relies on phonon-phonon interactions. Phonons contribute the the specific heat of a system: Cv = αT - βT3. Here, β refers to the phonon-phonon interaction contribution which only occur at high temperatures through thermal excitation. The specific heat capacity relates to the thermal expansion coefficient α for a system in the following equation[15]:
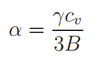
We can see therefore that as phonon-phonon interactions increase, the heat capacity increases causing the thermal expansion to increase.[16] This can also explain why at low temperatures the expansion is almost zero - there is insufficient thermal excitation for phonon scattering.
However, a diatomic with an exact harmonic potential would not have thermal expansion. This is due to the fact that in a harmonic system the harmonic phonons are temperature-independent, making the structure unchanging with increasing temperature[17], unlike the phonons in the QHA which are temperature dependent.
The thermal expansion coefficient can be calculated using the following formula:
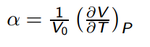
Using this formula and the results from the data above give a value of 2.68x10-5K-1. The literature results for the coefficient of thermal expansion vary depending on the temperature range used to calculate it. At a temperature range of 1273-2273K the coefficient was measured as 12.6±0.5x10-6K-1[18] This is far above the range used and so is not an appropriate value to compare the results with. Another literature source gave a range of 9-12x10-6K-1 for the minimum and maximum expansions over a wide temperature range.[19] The computed result is out by one order of magnitude, and clearly is higher than experimental results. We can attribute this however to the approximations used to get the results. Our approximations exclude the interactions of electrons and deals with interactions of atoms as single point charges which are approximated with a simple coulombic potential. With such a high degree of approximation going into our models, we can expect to have numerous inaccuracies with results.
When the temperature approaches the melting point of MgO - 3,125 K[20] - we expect that the ions move more freely as they break from the periodic lattice and have more motion as a liquid. It has been found however that the acoustic phonon modes stiffen[21]. This is therefore contradictory to the real motions of the ions and is not a good representation.
Molecular Dynamics
MD results
Similarly to the QHA the cell size is an important factor to accuracy and time cost of calculation. For this model a cell of 32 MgO units will be used. The results are shown below:
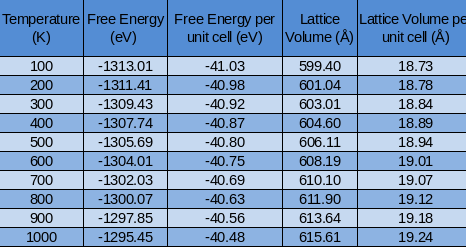
The value at 300K is -2.47x1025eV/mole per unit cell and is also close to literature values previously listed. The graph below compares the Free energy at different temperatures computed by both the MD and QHA theories.
The previous section discussed that the QHA loses free energy as temperature increases. It does not however decrease linearly and this is due to the -TdS term. Entropy is also dependent on the number of states available Ω:
Ω is related to the patition function Q,which equals:
The entropy is now has an intrinsic relation to temperature so this gives the Free Energy the slight logarithmic curved quality. However in the MD approximation free energy increases with temperature. This is due to the MD basis in classical physics, where the relationship with energy and temperature is linear:
The first term in this equation relates to kinetic energy of the system. It is easy to see then that as temperature increases, kinetic energy increases as expected and so the total energy also increases. Below the results for the MD computation of lattice volume are shown with the results from the quasi-harmonic approximation.
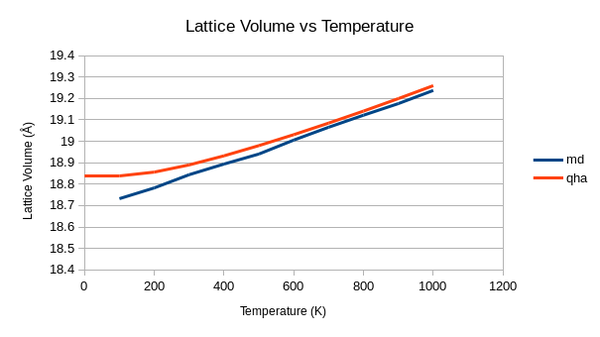
The MD graph is far more linear than the QHA. A value at 0K could not be calculated with this software but we can see that MD approximation gives lower values for the volume but the calculated thermal expansion coefficient - 3.22x10-5K-1 - is higher than the one predicted for the QHA. This value is still far away from experimental data due to the limitations of the MD model. MD's basis and real time atom movements makes it far more advanced than the calculations form the QHA. However using Newtons law to move atoms rather than Shrödinger's equation can become problematic especially at low temperatures when quantum effects become important. Another key problem is the 'force-field' potentials that are selected to run the simulations on. They need to realistically simulate the behaviour of a real system which is a difficult task.[22] In our simulations a Buckingham potential was used, this is a simplified version of the Lennard-Jones potential[23], which if used may lead to more accurate results.
Comparing MD and quasi-harmonic methods
The differences between the quasi-harmonic and MD calculations only continue. MD calculations take into account phonons across the Brilloin zone and not just the acoustic modes k to 0. MD theory importantly also includes anharmonicity to its calculations, which are neglected by quasi-harmonic calculations.[24]. Anharmonicity is responsible for the finite lifetime of phonons and their temperature dependence[25]. Due to this temperature dependence at high temperatures where intrinsic anharmonicity become important to the phonons, quasi-harmonic approximations break down, while MD become almost exact[26]. This can be seen in the divergence of both lines toward higher temperatures.
Other Considerations
The size of a cell needed to perform reliable MD for MgO can be related to previously experiments calculating the Free Energy. In this previous section it was seen that smaller grid sizes overestimated the values of the free energy, but grids that are too large have too high a computational cost. In MD, the computational cost is far larger than using the QHA so we are more limited to the size cell we can use. While using the cell size of 32 atoms gave us the correct relationship we expected with temperature it still yielded results that were not supported by literature values. A larger cell size such as 40 would improve this value, but the computational cost would be high.
We have previously discussed that at high temperatures the QHA breaks down as it ignores intrinsic anharmonicity. The following figure is adapted from experiments showing the thermal expansion of perovskite. LD refers to the QHA and MD the Molecular Dynamic calculations.

We can see that as temperature increases the QHA becomes exponential and we can assume that the MgO cell volume at high temperatures would also grow exponentially. If the cell was modeled with the MD approach, we can also assume looking at this graph that the cell volume would continue to expand at a steady rate. This is where MD also breaks down failing to model for the liquid melting point of MgO.
Conclusion
In this experiment we have computed the Free Energy and Thermal Expansion coefficient for MgO using MD and QHA calculations. First a suitable cell size was found to undergo calculations. This cell needed to be big enough for accurate results but not too big to be computationally expensive. Grids that are too small overestimate energies in the system, while larger grids get closer to the minimum energy. It was decided to use a 20x20x20 grid and the overall results of the experiments with literature comparisons are shown below:
| Total Free Energy (eV/mole per unit cell) | Thermal Expansion Coefficient (K-1) | |
|---|---|---|
| QHA | -2.46x1025 | 2.68x10-5 |
| MD | -2.47x1025 | 3.22x10-5 |
| Literature | -3.12x1025 | 9-12x10-6 |
All these results differ from literature values with the MD having closer values than the Quasi-Harmonic approach. At 300K, the free energy computed by the QHA is similar to the one modeled by MD, however at higher temperatures the entropic terms become large and the free energy decreases. This does not occur in MD calculations due the linear association with temperature, and Free energy increases with temperature. We can rationalise the differences in the thermal expansion coefficients by looking at the theory behind the calculations. The QHA is based in quantum mechanics, but does not include anharmonicity into its calculations. The phonon interactions become more important as temperature increases and without the associated anharmonicity terms in the calculation, the QHA breaks down. The MD theory however does include this anharmonicity and so at high temperatures it accurately models the system. The MD while mirroring correct trends also gives inaccuracies arising from the theories classical roots. Ignoring quantum effects makes this theory limited and with simplistic force potentials modelling interactions between atoms we can expect the results to be different to literature. At high temperatures MD can be seen as more reliable with added anharmonicity constants, while at lower temperatures the QHA is more accurate with added quantum effects.
While the limitations of the MD and QHA models can not reproduce experimental results on this scale (higher computer processing power could allow for larger grids to be calculated on), it is still a powerful method that allows us to see how temperature affects the MgO lattice.
References
- ↑ T.S.Bush, J.D.Gale, C.R.A.Catlow and P.D. Battle J. Mater Chem., 4, 831-837 (1994)
- ↑ Cho Yen Ho, Richard Erwin Taylor ASM International, 1998
- ↑ Zhu, Q. Crystal Structure Prediction and its Application in Earth and Materials Sciences, 2013
- ↑ Marx, D., Ab Initio Molecular Dynamics (2009)
- ↑ Scalies, R., Southern Methodist University (2012)
- ↑ Samiullah. M, Oxford University Press, 2015
- ↑ Nicola Manini Springer, Jan 14, 2015
- ↑ Jens-Boie Suck, M. Schreiber, P. Häussler, Springer Science & Business Media, Jul 23, 2002
- ↑ Hoffmann, R. (1987), How Chemistry and Physics Meet in the Solid State. Angew. Chem. Int. Ed. Engl., 26: 846–878. doi:10.1002/anie.198708461
- ↑ Herreros, B., The X-Ray Diffraction Zeolite Database
- ↑ Cooke, D., Parker, S., Osguthorpe, D., Physical Review, (2003)
- ↑ John Kotz, Paul Treichel, John Townsend, David Treichel Cengage Learning, Jan 27, 2014
- ↑ H. Chon, S.-K. Ihm, Y.S. Uh Elsevier, Dec 4, 1996
- ↑ Smoke, E. J. (1951). "Ceramic compositions having negative linear thermal expansion". Journal of the American Ceramic Society 34 (3): 87–90
- ↑ Pat, School of Physics, Peking University (2016)
- ↑ C M Kachhava New Age International, Jan 1, 2003.
- ↑ Frank Y. Fradin Elsevier, Oct 22, 2013
- ↑ Engberg, J. C. (1959). "Thermal Expansion of Al2O3, BeO, MgO, B4C, SiC and TiC above 1000°C". Journal of the American Ceramic Society 42 (6)
- ↑ Magnesia Properties and Applications, AZoMaterials (2000-2016)
- ↑ M.H.G. Jacobs, H.A.J. Oonk Springer Science & Business Media, Mar 2, 2012
- ↑ D. Y. Chung, D. J. Gunton, and G. A. Saunders Phys. Rev. B 13, 3239 – Published 15 April 1976
- ↑ N. W. Ashcroft, N. D. Mermin, Solid state physics, Brooks Cole, 1976
- ↑ R. A. Buckingham, The Classical Equation of State of Gaseous Helium, Neon and Argon, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 168 pp. 264-283 (1938)]
- ↑ A.R. Oganov et al. / Physics of the Earth and Planetary Interiors 122 (2000)
- ↑ Baddorf, A. P., Plummer, E. W., Surface anharmonicity, Elsevier, 1990
- ↑ Hideo Aoki, Yasuhiko Syono Cambridge University Press, Sep 25, 2000
- ↑ Artem R Oganov John P Brodholt G David Price Physics of the Earth and Planetary Interiors , 2000, Vol.122(3-4), p.277-288