Rep:Mod:sm17121

Transition States and Reactivity

The Transition state corresponds to the highest energy along a reaction coordinate and is the least stable point. Gaussian Software can be used to identify transition states in reactions and their preferred conformations and pathways. In this experiment the Cope rearrangement of 1,5-hexadiene will be examined, studying the conformations of the reactant and the chair and boat transition state structures and their relative activation energies. The Diels Alder reaction of Ethylene and cis-Butadiene and of Cyclohexa-1,3-diene and Maleic Anhydride will both be examined, looking at orbital mixing and the endo and exo preferences. Two modelling methods will be used, The Hartree Fock Method and the B3LYP method. The Hartree Fock (HF) theory is based on one-electron spin-orbitals to solve the Schrodinger equation by using an iterative numerical procedure, continuing until there is no change in the significant figures. The B3LYP Method is a 'hybrid functional' which is applied in Density Functional Theory (DFT). It is a more advanced theory than HF, as it optimizes electron density rather than a wave function. HF assumes that each electron sees eachother but does not consider their interactions while the B3LYP method does, making it a more powerful method.

Both methods will be used and compared throughout this experiment.

Nf710 (talk) 11:26, 5 November 2015 (UTC) Very good understanding! HF used a mean potential field for the electronic repulsion term where as DFT used a function of the electron density to appropriate the potential felt on each electron.

The Cope Rearrangement

The Cope Rearrangement of 1,5-hexadiene is an example of a [3,3]-sigmatropic shift. We can use computer modelling study the low-energy minima and transition structures and find the preferred mechanism and structures.

The Cope Reaction

Optimizing conformers of 1,5-hexadiene

There are twelve conformers of 1,5-hexadiene, of varying Gauche and Antiperiplanar conformations. In GaussView six of these conformers were modeled and analysed. The table below show the structure, point group and energies of each structure found.

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy kcal/mol
Anti 1	Anti 1	C2	-231.692602	0.04
Anti 2	Anti 2	Ci	-231.692535	0.08
Anti 4	Anti 4	C1	-231.69097	1.06
Gauche 1	Gauche 1	C2	-231.687716	3.1
Gauche 2	Gauche 2	C2	-231.691667	0.62
Gauche 3	Gauche3	C1	-231.692661	0.00

It can be seen from the table that Gauche 3 is the lowest energy conformer and therefore would be expected to be the most common conformer. This stability can be explained by interaction between the C=C π orbital and the vinyl proton. Gauche 1 has the highest energy and is therefore the most unstable conformation. This is due to the close proximity of the electron rich vinyl groups creating a large repulsion between them. The Gauche conformers as a trend decrease in energy with increasing distance between the vinyl groups, lowering repulsion and increasing stability. The energies of the anti conformers are related to the distance between the protons on the β carbon and the vinyl protons, with the same principle of proximity leading to repulsion; the anti conformers with a larger proton-proton distance are lower in energy and therefore more stable.

Nf710 (talk) 11:28, 5 November 2015 (UTC) good explanation, You could have improved on this by actually showing the orbital overlap graphicallly from the .chk file.

Comparing HF/3-21G and B3LYP/6-31G*

The Antiperiplanar 2 conformer was re-optimized using the B3LYP/6-31G* theory. Below shows the contrasting optimization results in comparison to the original HF/3-21G optimization. Angle 1 denotes the angle between the C1-C2-C3 while angle 2 denotes the angle between C2-C3-C4. Below shows a diagram of the molecule with each atom labelled for clarity.

Numbered Molecule

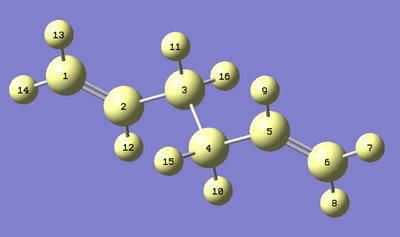
Optimization	Length C1-C2 (Å)	Length C2-C3 (Å)	Length C3-C4 (Å)	Dihedral Angle 1 (°)	Dihedral Angle 2 (°)
HF/3-21G	1.316	1.509	1.553	114.65	179.99
B3LYP/6-31G*	1.338	1.507	1.555	118.78	180.00

The B3LYP theory gives a longer bond length for the C1-C2 double bond in comparison to the HF/3-21G. This longer bond length is consistent to the literature values for a carbon-carbon double bond of 1.33Å. While it also gives larger C4-C5 and a smaller C3-C4 bond lenths, the overall difference between these bonds are negligible.

The dihedral values also vary.The B3LYP theory returns a larger angle between C1-C2-C3 then the Hartree-Fock method, while the C2-C3-C4 angles remain almost identical.

Nf710 (talk) 11:30, 5 November 2015 (UTC)Good analysis on geoms

Frequency Analysis

Using the B3LYP optimized antiperiplanar 2, a frequency calculation can be run to confirm all vibrational frequencies are real and positive and that it is indeed the minimum conformer and the critical point for 1,5-hexadiene. The frequency derived is related to the second derivative of the potential energy surface (PES) of this conformer - this can give us further information about this stationary point of the PES.

The log file from this analysis can be found here. It confirms that this structure has been optimized to a minimum energy, with all real and positive vibrational frequencies. The table below shows the summation of some energies extracted from the log file.

Energies/Enthalpies Added	Total Energy/Enthalpy
Electronic and Zero-point Energies	-234.416255
Electronic and Thermal Energies	-234.408963
Electronic and Thermal Enthalpies	-234.408019
Electronic and Thermal Free Energies	-234.447872

Nf710 (talk) 11:35, 5 November 2015 (UTC)Your energies are correct and you have stated that the frequencies should be positive. your undertsanding of this is nearly there. the second derivative is the force constant which is used in the equation of a quantum harmonic oscillator, it is square rooted. so therefore if you have a negaive k it will be an imaginary frequency.

Optimizing the "Chair" and "Boat" Transition Structures

Chair Optimization: Hartree Fock Method

The chair transition state was optimized first using the HF theory. An allyl fragment was modeled and optimized and doubled, set at 2.2Å and placed to form a C2h point group. This transition state structure was further optimized with the TS (Berny) method and finally the HF method was used to perform a frequency analysis. For a correct transition state, an imaginary vibration of -818cm^-¹ can be found in the log file and then visualized. Both the optimized transition structure and -818cm^-¹ vibration are displayed below:

Optimized Structutre	-818cm-¹ Vibration
	Lowest positive vibration

Chair Optimization:Frozen Coordinate Method

Now we can optimize this structure further to a minimum. This was done first by freezing the terminal bonding ends at 2.2Å , and then by leaving them free to move.

Terminal Ends Frozen	Terminal Ends Free

When comparing both structures, we can see that leaving the terminal bonding ends free increases the distance marginally to 2.208Å. The internal carbon bonds also increase slightly, from 1.381Å to 1.389Å. The frequency value however increases from -817.87 to -817.93. These differences appear negligible, but we can see that overall the Hartree Fock optimization described previously is more reliable and closer to the desired distances and frequencies than the frozen coordinate method.

Nf710 (talk) 11:38, 5 November 2015 (UTC) The frozen co ord method still uses HF it just freezes the coord, you are still using HF to do the optimisation.

Boat Optimization: QST2 Method

To find an optimized boat conformer transition state we can now use the QST2. In this method we can specify the reactants and products for a reaction and run a calculation which will find the transition state between them. Below shows the first input for this method which was unnsuccessful due the limitations of the program; not rotating the cental carbon carbon bond and instead breaking it. The input then had to be modified to allow the program to converge to the right structure, this is also shown below.

First Input
Modified Input

The transition state was confirmed with a single negative vibration of -840.09. The structure and corresponding vibration are shown below:

Transition state structure

Lowest positive vibration

Intrinsic Reaction Coordinate

By mapping the Intrinsic Reaction Coordinate, we can determine the conformer produced from the transition state.This computational method tracks the minimum energy path from a transition structure to its minimum on a PES, by following where the gradient of the energy surface is steepest.The IRC plots this reaction path, and is displayed below.

The IRC found for this transition state did not reach a minimum although it shows that the energy has reached a plateau. To find the final minimum geometry an optimization was performed on the lowest energy structure produced by the IRC. After comparing this optimized structure with previously found conformers, it was found to be very similar to the Gauche 2 conformer. The minimum energy coordinate was then confirmed to be Gauche 2. Both these conformers are shown below for comparison.

Optimized Minimum Energy Conformer

Gauche 2 Conformer

Nf710 (talk) 11:41, 5 November 2015 (UTC) That doesnt look like it has converged to me and therefore you couldnt use the energy in the log file to directly determine which conf it is.

Activation Energy

Both transition states can be analysed to see which has the lowest activation energy and therefore is the preferred transition state. First both conformations were optimized again via a frequency optimization using the B3LYP method. The resulting transition states were compared with Hartree Fock optimizations and are summarized below.

Transition state and Method	Structure	C1-C2-C3 Angle (°)	C1-2 length (Å)	C1-4 length (Å)
Chair: Hartree Fock		120.53	1.389	2.021
Chair: B3YLP		121.92	1.381	2.20
Boat: Hartree Fock		121.68	1.381	2.14
Boat: B3YLP		121.67	1.381	2.14

In each case the transition state was found. From the table above you can see that for the chair conformation the results between the two methods vary substantially while for the boat conformation they are almost identical. Next the energies of each transition state were collated into the table below. Using the reactant energies of Anti 2, the activation energies for each transition state at each level of theory were found.

Nf710 (talk) 11:43, 5 November 2015 (UTC) you havent explicitly states the frequencies to say they are defiantly TSs.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619320	-231.466705	-231.461345	-234.585000	-234.414217	-234.413557
Boat TS	-231.602802	-231.450927	-231.445298	-234.556110	-234.404607	-234.398685
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.559705	-234.468100	-234.461787

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	33.81	30.26	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	39.84	39.59	44.7 ± 2.0

When comparing to experiment, the higher level of theory gives more accurate results, while they are still not close to experimental values. The activation energy is highest at 0K, which is expected with less thermal energy to help get over the energy barrier then that at 298.15K. Overall the chair transition state has lower activation energy and can therefore be reliably assumed to be the preferred state.

Nf710 (talk) 11:49, 5 November 2015 (UTC) you haven't deduced that geometries need a smaller basis set as they dont change that much but energies do change alot with basis set. Alot your energies for BY3LP seem a bit out. In all a good report with a decent level of undertanding, it was just unfortunate how you must have been at the wrong local minimum in your calculation.

The Diels Alder Cyloaddition

Ethylene and cis-Butadiene

The Diels-Alder reaction is a cycloaddition reaction between a diene and a dienophile. It is used in many different reactiosn but here we will be studying the reaction between ethylene and cis-butadiene to form cyclohexene.

The Diels Alder Reaction

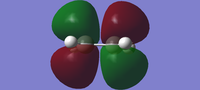
The structures of ethylene and cis-butadiene were optimized using the Hartree-Fock theory. The LUMO and HOMO orbitals could then be viewed, and both are displayed in the table below.

	Cis-Butadiene	Ethylene
Structure
HOMO	Anti-symmetric to the plane	Symmetric to the plane
LUMO	Symmetric to the plane	Anti symmetric to the plane

The transition state for the reaction was optimized using the Hartee Fock theory. A single negative vibration shows that this is indeed the transition state. Below shows the structure, and bond lengths for this transition state:

Structure
Labelled diagram
C1-C2 bond length Å	1.37
C2-C4 bond length Å	1.39
C4-C5 bond length Å	2.21
C5-C6 bond length Å	1.38

The single C-C bond lengths in sp² and sp³ hybridisation ar 1.46Å and 1.54Å respectively. All the C-C bonds in this transition state are less than both suggesting delocalisation across both reactants. The distance between the terminal bonding carbons are 2.21Å. When comparing to the Van der Waal radius of a carbon atom of 1.70Å, it is clear that there is bond between them, expected of the final sigma bond outcome.

The vibration corresponding to the reaction path shows a synchronus bond formation, typical of the pericyclic mechanism expected in the Diels Alder Mechanism. The lowest positive frequency vibration (166.50) is asynchronus in its bond formation. Both vibrations are shown below for comparison.

(There will be no bond formation through this normal mode. The positive frequency indicates that it is stable with respect to the normal mode. Don't forget to put units in (cm^-1) Tam10 (talk) 11:48, 28 October 2015 (UTC)

Transition State Vibration

Lowest positive vibration

(It seems you've used the wrong frames for your vibrations in the script. Not an issue as we don't expect you to use script. However you should report your vibrational frequencies - I almost thought you had the wrong structure. Tam10 (talk) 11:48, 28 October 2015 (UTC))

The HOMO and LUMO of the transition state is shown below, with the MO's of butadiene and ethylene used to form them. This reaction is allowed as HOMO and LUMO orbitals are of similar energy and mix well. Following The Woodward Hoffman rules, there are zero antarafacial components and one suprafacial component. It therefore follows the rule that (4q+2)_s + (4r)_a must be odd.

Transition state orbital	Contribution from ethylene	Contribution from cis-butadiene
Homo: Anti-symmetric to the plane	LUMO	HOMO
LUMO: Symmetric to the plane	HOMO	LUMO

Woodward Hoffman Analysis

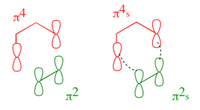
Cyclohexa-1,3-diene and Maleic Anhydride

In Diels Alder reactions, the product is typically an Endo structure. This part of the experiment will analyse the orbitals of two reactants to determine why this is, and if it is indeed true. The transition state of the diels alder reaction between Cyclohexa-1,3-diene and Maleic Anhydride was modeled using Hartree Fock theory. First both Cyclohexa-1,3-diene and Maleic Anhydride were optimised and their HOMO and LUMOs can be found below:

	Cyclohexa-1,3-diene	Maleic Anhydride
Structure
HOMO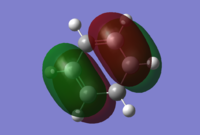
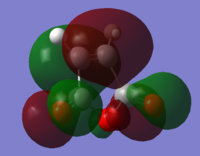
LUMO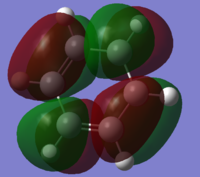

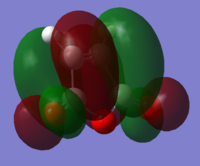
The Exo and Endo transition states were modeled with the optimized reactants and confirmed by a single negative vibration. The structures, energies and HOMO and LUMOs are shown below. The bond lengths were also measured and are displayed in a separate table.

	Exo Transition state	Endo Transition state
Structure
Relative Energy	0.66	0.00
HOMO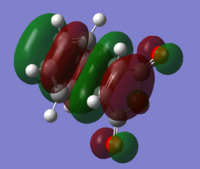
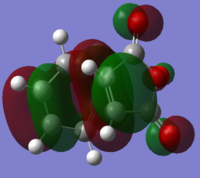
LUMO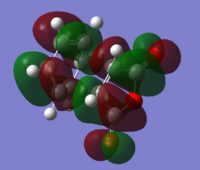

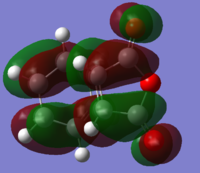
Below is a labeled structure of a transition state for clarity.

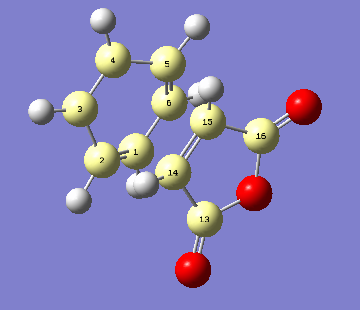
Bond	Endo Bond Length Å	Exo Bond Length Å
C1-2	1.434	1.431
C2-3	1.431	1.434
C3-4	1.345	1.343
C1-6	1.343	1.345
C14-15	1.395	1.395
C14-13	1.486	1.486
C2-14	2.108	2.129

The relative energies of both structures indicate that the endo structure is more stable. When comparing the bond length data, the only substantial difference between both structures is where the new bonds form - the exo transition having a longer bond distance than the endo. This suggests strain in the exo form which could be caused by the proximity of the carbonyl groups on the maleic anhydride to axial hydrogens on the diene. The expected transition state follows the 'endo rule'. This can be attributed to the presence of electron density found in the HOMO of the endo transition state which is absent in the exo state. This overlap of charge stabilizes the endo state and makes it more prefered. This is often reffered to as the secondary orbital overlap effect.

(Calculate and include activation and reaction energies in relatable units (KJ/mol or Kcal/mol) Tam10 (talk) 11:48, 28 October 2015 (UTC))

Conclusion

The transition states and conformations were studied using Gaussian at two levels of theory, Hartree Fock and B3LYP. For the Cope Rearrangement, six conformers of the reactant 1,5-hexadiene were modeled and analysed with Gauche 3 being the resultant lowest energy conformer. When comparing both theories to the Anti 2 conformation, B3LYP was found to be more consistent with literature than HF as expected as a higher level theory.

The chair and boat transition structures were found and optimized for the transition states. They were compared and optimized using different theories and the activation energies were found. The chair transition state was found to have the lowest energy and therefore the prefered mechanism. Comparing again HF and B3LYP theory, the higher level theory was found to give more accurate results when compared to experimental values.

Two Diels Alder reactions were studied computing the energies of the endo and exo transitions states and modelling the HOMO and LUMO for each. By comparing HOMO's the endo transition state was found to be the prefered mechanism in the reaction of cyclohexa-1,3-diene and maleic anhydride, with their orbital projections helping explain secondary orbitals effects.

The Gaussian program is a powerful computational method to study molecules and their reactions. This experiment showed a variety of tools available through computational chemistry to model complex systems and reactions. Two theoretical methods were used and compared to show the advancement of modern computational methods and their uses.