Rep:Mod:slippynipps3

Module 3

Nicholas Browning

The Cope Rearrangement

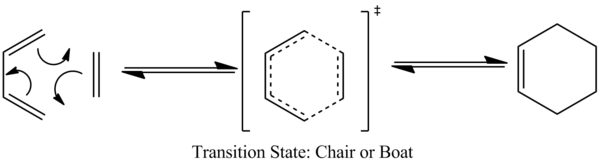
The underlying chemistry of the cope rearrangement has been extensively studied both experimentally and computationally. It is understood to be a [3,3] sigmatropic shift reaction which proceeds with one σ bond broken and one made in a concerted fashion. Although this reaction is both pericyclic and concerted, it's reaction coordinate can be considered to travel through a transition state which adopts "chair" or "boat" geometry.

Optimizing The Reactants and Products

In order to understand the transition state via which the Cope rearrangement proceeds, we must first understand the geometric properties of the reactant molecule. Several conformers of 1,5-hexadiene were optimized in GaussView at the HF/3-21G level of theory. This was achieved using the following calculation on each conformer.

#opt hf/3-21g geom=connectivity

The approximate symmetries of each isomer was then calculated using the "Symmetrise" method, and the results are shown in Table 1.

'Table 1: Conformations of 1,5-hexadiene'

	Anti 1	Anti 2	Gauche 1	Gauche 3
	Cope Anti 1	Cope Anti 2	Cope Gauch 1	Cope Gauch 2
Energy (a.u)	-231.69260225	-231.69253524	-231.68771613	-231.69266118
Point Group	C2	Ci	C1	C1

Gauche 3 is most energetically stable. This mode limits steric repulsion comparatively to gauche 1, and presents a C-H σ* - C=C π orbital overlap that is less clearly defined in the anti 1 conformer . The Anti 2 conformer was then optimised using the more accurate DFT B3LYP/6-31G* level of theory. This was achieved with the following calculation:

#opt rb3lyp/6-31g(d) geom=connectivity

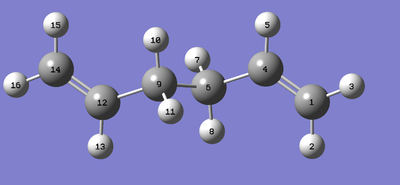
The following image is used as a as a reference for the labelling referred to in Table 2.

A comparison between two levels of theory is shown below in Table 2.

'Table 2: B3LYP Optimised Anti 2 Conformer'

Calculation	Energy / a.u	Point Group	C=C Bond Length / Å	C1-C4-C6 Angle	C4-C6-C9 Angle
HF / 3-21G	-231.69253524	Ci	1.316	124.82	111.35
B3LYP / 6-31G*	-234.61171035	Ci	1.334	125.29 o	112.68

The energies of the two conformers are markedly different, which asserts the higher level of accuracy when using the more complex basis set of the B3LYP method. The molecule still retains the same geometry with both basis sets, and hence point group. Similarly all bond lengths remain approximately the same, apart from the C=C bond length which indicates that the 3-21G basis set is somewhat inaccurate in representing the substituted double bonds.

A Frequency calculation was then run to confirm the structure of the Anti 2 conformer was at a minimum Energy. This is the case when no imaginary vibrations are calculated. The frequency calculation was achieved using the following command:

#freq b3lyp/6-31g(d) geom=connectivity

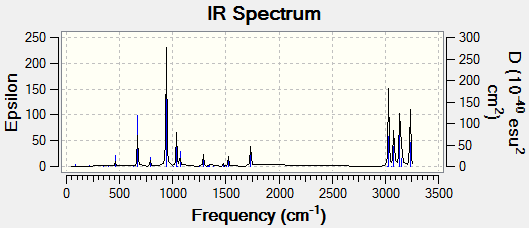
Selected vibrations have been taken from the IR spectrum, shown below, and displayed in Table 3.

'Table 3: Vibrations of Anti 2 Conformer'

Mode Number	32	34	36	38	39
Frequency	1734.31	3031.47	3080.23	3136.92	3155.47	3233.90
Intensity	18.13	53.59	35.79	56.15	14.71	45.47
Description	Asymmetric C=C Stretching	Asymmetric C-H2 stretching	Asymmetric C-H stretching	Asymmetric Alkene C-H stretching	Asymetric Alkene CH2 stretching	Asymetric Alkene CH2 stretching

There are no negative vibrations present, so the calculation was successful in finding a minimum in energy.

From the log file the energy of the molecule can be separated into potential and kinetic energy parts and from there the enthalphy and free energy of dissociation can be calculated. These parameters are temperature-dependent and so a calculation was run at 0 K as well as 298K to study the effect of temperature on the various energies, the results are tabulated below:

'Table 4: Thermodynamic Properties of Anti 2 Conformer'

Energies (a.u.)	298K
Zero-point correction	0.142507
Thermal correction to energy	0.149853
Thermal correction to enthalpy	0.150797
Thermal correction to gibbs free energy	0.110933
Sum of electronic and zero-point energies	-234.469204
Sum of electronic and thermal energies	-234.461857
Sum of electronic and thermal enthalpies	-234.460913
Sum of electronic and thermal free energies	-234.500777

The Sum of electronic and zero-point Energies is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE).

The Sum of electronic and thermal Energies is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans).

The Sum of electronic and thermal Enthalpies contains an extra correction for RT (H = E + RT), which is particularly important when looking at dissociation reactions.

The Sum of electronic and thermal Free Energies includes the entropic contribution to the free energy (G = H - TS).

Optimizing the "Chair" and "Boat" Transition States

The computational models of the 1,5-hexadiene reactant molecule were generated in the previous section, which allowed the discussion of the chair and boat transition states for the cope rearrangement.

Chair Transition State

The chair transition state was optimized using two methods. The first involved optimizing the hypothetical structure to a "TS (Benny)" rather than to a minimum, in which the force constant was computed once. The second method involved using a frozen coordinate system via the redundant coordinate editor.

Firstly two HF/3-21G optimized 1,5-hexadiene fragments were arranged in an approximate chair transition state heometry, in which the two fragments terminal carbons had an internuclear distance of 2.2Å. This gave what was needed to calculate the transition state with the two methods.

TS (Benny) Method

For this method the initial guess structure needed to be accurate as this calculation is sensitive to the structure of the input. If the input is not close enough to the transition state, the calculation will not produce the transition state geometry. However in this case, the transition state is known and therefore this method is very applicable. In the first optimization step the force constant matrix is calculated, and then recalculated at every step thereafter. Hence if the input is not close enough to the transition state geometry the potential energy surface of the reactant, combined with the force constant matrix, will not lead to the potential energy surface of the wanted transition state.

The calculation was achieved with the following command:

#opt=(calcfc,ts,noeigen) freq hf/3-21g geom=connectivity

The results are presented in table 5.

'Table 5: Chair TS (Benny) Geometric Properties'

Energy / a.u	Terminal C-C bond Length / Å	Cope Anti 2
-231.61932231	2.020

The energy of the optimized structure is 231.61932231 a.u, which is as expected lower than the energy of the boat transition state calculated below.

A frequency calculation was intrinsically calculated using the values above due to the "freq" keyword, and hence no additional method was required to calculate the vibrational frequencies of the transition state.

The addition of "Opt=NoEigen" saves the calculation from crashing if more than one imaginary frequency is found during optimization. This is a safety feature to ensure that even if geometry of the input molecule is quite different to the TS, it may still reward the desired geometry.

The results shown below in Table 6.

'Table 6: Chair TS (Benny) Vibrational Properties'

Frequency / cm-1	Intensity	Animation
-817.96	5.88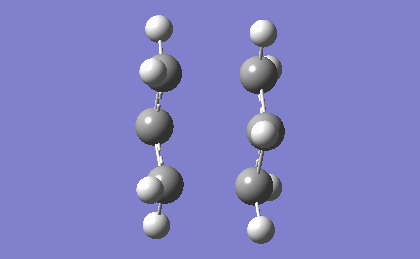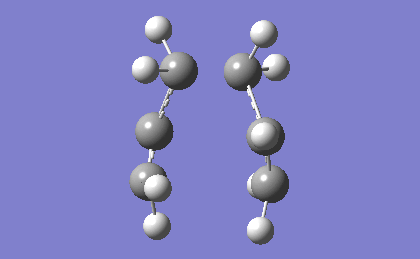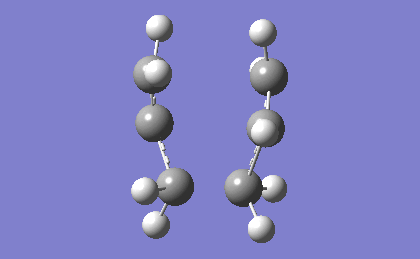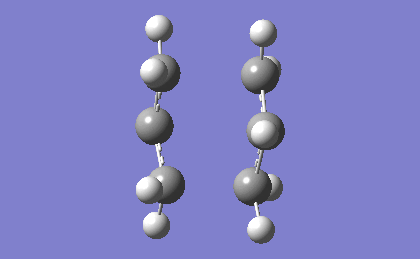

The frequency analysis confirms the successful optimization to the chair TS through the presence of an imaginary vibration at -817.96 cm^-1. This vibration in fact corresponds to the Cope rearrangement as there is a vibration along the bond to be formed and an antisymmetric vibration along the bond to be broken during the rearrangement, indicating a concerted pericyclic mechanism.

Frozen Coordinate Method

The distance between the two fragments of 1,5-hexadiene was frozen at 2.2Å through the redundant coordinate editor, which allowed all but the bonds being made and broken to be optimized. Once this optimization was complete, this distance was allowed to change, again through the redundant coordinate editor and the whole molecule was re-optimized. This calculation does not require the whole Hessian matrix to be be computed - purely differentiating along the reaction coordinate provides a good enough approximation for the initial force constant matrix. Although this seems a somewhat lengthy process, for complicated systems this method can save a significant amount of time.

The method gave a value for the energy of -231.61932199 a.u and a 1,5-hexadiene terminal bond length of 2.019 Å. Both these values are very close to that returned by the TS (Benny) method indicating that both are appropriate in determining the transition state properties of this rearrangement.

Both of the methods above have their advantages and disadvantages. The frozen coordinate method can shorten the time of calculation for larger systems, however it requires a good estimation of the terminal distances between the two fragments. Comparatively this distance need not be known for the TS (Benny) method. This method requires that the initial structure of the proposed transition state must be reasonably comparable to the actual geometry, and hence one must know roughly what the transition state looks like, which is not always possible.

Boat Transition State

For this optimization the QST2 method was used. This method involves specifying the reactants and products of the reaction and allowing the calculation to interpolate between the two structures, with the aim to find a transition state somewhere between the two states. This calculation has a geometric constraint, in that the TS must be of similar structure to both the reactant and product. This constraint was demonstrated during an initial optimization in which the reactant and product geometries were both incorrect, which resulted in a failed calculation.

Both reactant and product were remodelled such that the central C-C-C-C dihedral angle was set to 0^o and the central C-C-C angles to 100^o.

The method was then run using the following command:

#opt=qst2 freq hf/3-21g geom=connectivity

The results are shown in table 7.

'Table 7: Boat QST2 Geometric Properties'

Energy / a.u	Terminal C-C Bond Length / Å	Cope Anti 2
-231.60280244	2.140

The energy of the Boat TS was calculated to be -231.60280244 a.u. This is significantly higher than the chair transition state energy of 231.61932231 a.u. The C-C bond length is also found to be 0.06Å lower than that found in the chair structure, indicating an increasing amount of steric destabilization contributing to the energy.

To confirm whether this transition state was successfully reached a frequency analysis is necessary. Similarly to the chair optimization a frequency calculation was not needed to be run separately due to the "freq" keyword in the command above. The results of the frequency analysis shown in table 8.

'Table 8: Boat QST2 Vibrational Properties'

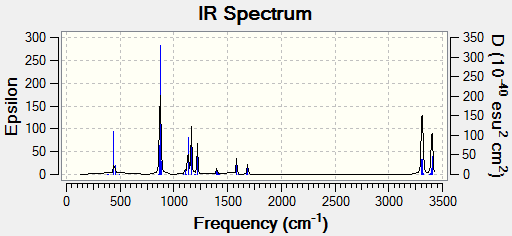
Frequency / cm-1 !! Intensity  !! Animation
-839.98	1.62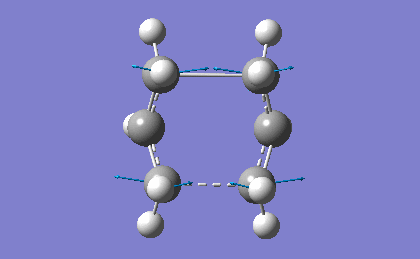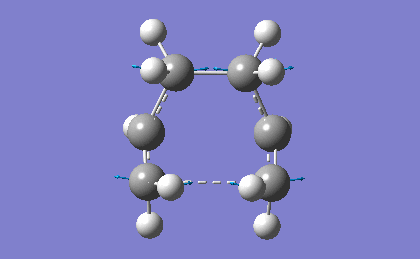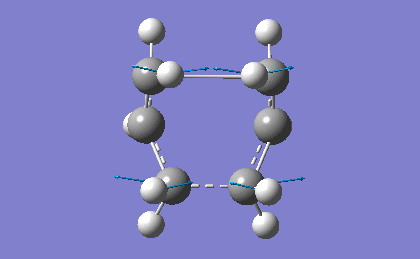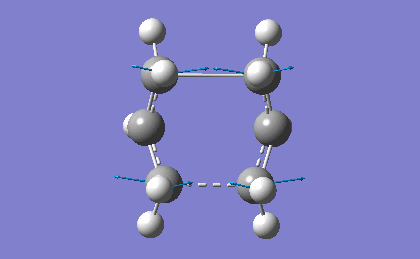

The frequency analysis confirms the successful optimization to the Boat TS through the presence of an imaginary vibration at -839.98 cm^-1. This vibration again corresponds to the bond formation during the Cope Rearrangement, as expected.

Intrinsic Reaction Coordinate (IRC) Method

This method is used to follow the minimum energy path from a transition state to it's local minimum on a potential energy surface. This method creates a series of points by taking small geometrical incrementation in the direction where the gradient of the energy surface is largest. This method tells us which conformers of the 1,5-hexadiene reactant are connected to the transition structures.

This calculation was first run on the HF/3-21G level of theory, with 50 points set as the length of the IRC pathway, and the force constants were calculated once. This was achieved using the following command on the optimized chair structure:

#irc=(forward,maxpoints=50,calcfc) hf/3-21g geom=connectivity

The results are shown below in table 9.

'Table 9: IRC Trjajectory of Boat Transition State'

Final Step Geometry	Total Energy	RMS Gradient
Cope Anti 2

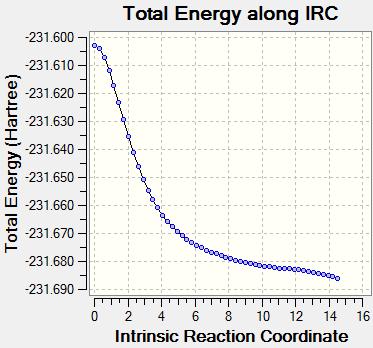
The energy of the last step was found to be -231.67723884 a.u. This is a much lower energy than that found from the QST2 method (-231.60280244 a.u). When compared to the geometries for the 1,5-hexadiene fragments, it can be seen from the geometry of the molecule in the final step of the calculation that the local minimum has not been yet reached. It was decided that in order to reach the desired reactant geometry, the force constant should be calculated every step, thus allowing the method to determine whether or not it's moving along the minimum energy pathway, and be able to correct it's trajectory if it is not. The command used to calculate this is shown below.

#irc=(forward,maxpoints=50,calcall) hf/3-21g geom=connectivity

The results are shown in table 10.

'Table 10: IRC Trjajectory of Boat Transition State'

Final Step Geometry	Total Energy	RMS Gradient
Cope Anti 2

The energy resulting from the final step in this calculation is -231.68599666 a.u. This energy did not closely match any of the conformations listed in the wiki table. It was decided to increase the number of points on the IRC pathway to 75. The results are shown in table 11.

'Table 11: IRC Trjajectory of Boat Transition State'

Final Step Geometry	Total Energy	RMS Gradient
Cope Anti 2

The resulting energy is now -231.69266035 a.u from 76 step calculation. This energy closely matches the gauche 2 conformer from the wiki table. To confirm this, the number of points along the IRC pathway was increased to 100, which again produced the energy of -231.69266035 a.u, having only reached 76 steps. Therefore, the boat transition structure is reached in the cope rearrangement if and only if the reactant is in the gauche 2 geometry.

Activation Energy for Chair and Boat Transition States

The HF/3-21G Structures of both Chair and Boat transition states were optimized to a more accurate structure using the TS (Benny) method with DFT/B3LYP/6-31G(D) level of theory. A comparison between the thermodynamic properties produced from each method is shown in Table 11.

'Table 11: Thermodynamic Properties of Chair and Boat Transition States'

	HF/3-21G			B3LYP/6-31G*
	Electronic Energy	Sum of Electronic and Zero-Point Energy	Sum of Electronic and Thermal Energy	Electronic Energy	Sum of Electronic and Zero-Point Energy	Sum of Electronic and Thermal Energy
		at 0 K	at 298 K		at 0 K	at 298 K
Chair TS	-231.61932201	-231.466705	-231.461337	-234.55698281	-234.414919	-234.409010
Boat TS	-231.60280248	-231.450929	-231.445309	-234.54309304	-234.402340	-234.396005
Reactant	-231.69253530	-231.539539	-231.532567	-234.61171035	-234.469203	-234.461857

From the thermochemical data the activation energies for both transition states and hence there pathways can be calculated. The calculated activation energies are shown below:

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298 K	at 0 K	at 298 K	at 0 K
ΔE (Chair)	45.70	45.942042911	34.06	34.342057174	33.5 ± 0.5
ΔE (Boat)	55.60	56.308206706	41.96	43.058021302	44.7 ± 2.0

For both levels of theory the values computed agree with those quoted in the wiki. It can be seen that that the chair TS is more stable than the boat TS and as a result, the chair TS has a lower activation energy than the boat TS and so, the chair TS is the expected TS for the Cope Rearrangement of 1,5-hexadiene. With the anti 2 conformr as the reactant and the gauche 3 conformer as the product.

The Diels-Alder Cycloaddition

The Diels-Alder Reaction is an example of a [4π+2π] pericyclic cycloaddition which occurs between a dienophile and a diene. By nature of the concerted pericyclic process, there are no intermediate species and there is only one transition state. The reason why the Diels-Alder reaction is so notable is that the reaction proceeds via a cyclic transition state, which contains 6 delocalised electrons which contribute aromatic character to the transition state, stabilizing it and speeding up the reaction overall.

The reaction occurs through the π-orbitals of the dienophile and the diene, forming two new σ-bonds in the process. The number of π-electrons involved in the concerted formation of the transition state determines whether the reaction proceeds in a concerted stereospecific fashion (allowed) or not (forbidden).

The aim of this mini-project is to analyse the geometric and molecular orbital properties of both the reactants and transition state, and use this information to understand the mechanistic details of the Diels-Alder reaction.

The Reactants: Cis-butadiene and Ethylene

The reaction of cis-butadiene and ethylene is a Diels-Alder pericyclic process in which 2 sigma bonds are formed, this is illustrated in the reaction scheme below.

Optimization of Reactants

Ethylene and cis-butadiene were optimized using the semi-empirical AM1 method. This was achieved using the following command:

# opt am1 geom=connectivity

The results are shown in table 14 below.

'Table 14: Geometric Optimization of Cis-butadiene and Ethylene'

	Cis-butadiene	Ethylene
Geometry	Cope Anti 2	Cope Anti 2
Energy / a.u	0.04879723	0.02619028
C=C Bond Length /Å	1.34	1.33

Molecular Orbitals of Reactants

Next, the frontier orbitals of the two reactants was calculated by using the "edit->MOs" functionality from the optimized .chk geometry files. The results are presented in table 15 below.

'Table 15: Molecular Orbitals of Cis-butadiene and Ethylene'

	Cis-butadiene	Ethylene
HOMO
LUMO
Symmetry	HOMO - Antisymmetric; LUMO - Symmetric	HOMO - Symmetric; LUMO - Antisymmetric
Energy / a.u	HOMO: -0.344; LUMO: 0.017	HOMO: -0.388; LUMO: 0.053

It can be seen from the above diagram that the symmetries of the HOMO and LUMO orbitals for ethylene and cis-butadiene are opposite. Due to conservation of orbital symmetry there are only two interactions that may result from these 4 orbitals. Firstly, the HOMO of the cis-butadiene and the LUMO of ethylene, and secondly the HOMO of ethylene and the lumo of cis-butadiene. Clearly orbital symmetry is important in pericyclic processes, as it determines which MO's are able to mix, and hence governs the stereochemical outcome of these reactions.

The Transition State

The TS (Benny) method described earlier was used to optimize the geometry of the cyclic transition state. The B3LYP/6-31G(d) level of theory was chosen due to it's high accuracy and efficient calculation time. It was decided that the force constant should be calculated at every iteration, and the keyword "Opt=NoEigen" was used to prevent the calculation crashing if more than one imaginary vibration was found.

Optimization of Transition State

The calculation was achieved using the following method:

# opt=(calcall,ts,noeigen) b3lyp/6-31g(d) geom=connectivity

The resulting geometric properties are described in table 16 below.

'Table 16: Structure of Cyclic Transition State'

Geometry	Energy / a.u	C-C Bond Forming Length / Å	C=C bond Length
Cope Anti 2	-234.54389655	2.27	1.39

A typical C=C bond length is 1.34 Å, which is very closely matched in both reactants. When comparing against table 15, we can see that the bond length of Ethylene fragment has increased from 1.33 Å to 1.39 Å in the TS, suggesting that the stabilising π bonds are breaking to form new C-C bonds. The new C-C bond formed in the TS has a bond length of 2.27 Å, which is closing to the typical C-C bond length of 1.54Å.

In cis-butadiene, the C_sp³-C_sp³ bond length is 1.45Å. This same bond in the TS state receives electron density via the ring forming process and hence is shortened closer to the value of a typical C=C bond length, 1.34 Å.

Frequency Analysis of Transition State

In order to confirm the success of the calculation, a frequency analysis was run. . This was achieved by going to "Results->Vibrations" and running a FreqChk, saving normal modes in the process. The resulting imaginary vibation is shown in table 17.

'Table 17: Vibrations of Cyclic Transition State'

Frequency	Intensity
-525.00	5.7949

The presence of the negative frequency shows that the TS was reached successfully. The vibration corresponds to the synchronous formation of two C-C bonds between the termini of the two reactants. This vibration compounds the fact that the Diels-Alder is a pericyclic reaction, as both of the new σ-bonds are formed in a concerted fashion.

Molecular Orbitals of Transition State

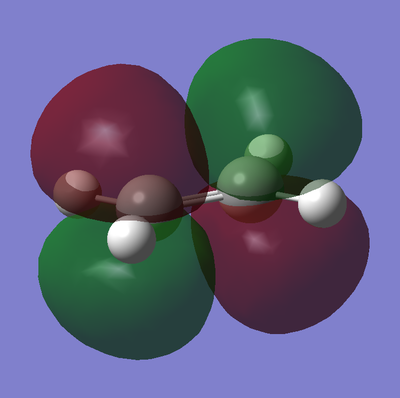
The frontier orbitals of the transition state are shown below in table 18.

'Table 18: Molecular Orbitals of Cyclic Transition State'

Molecular Orbital	HOMO	LUMO
Graphic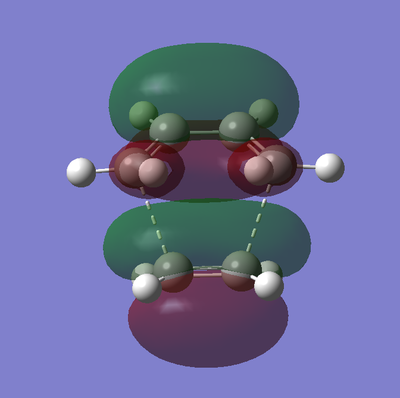
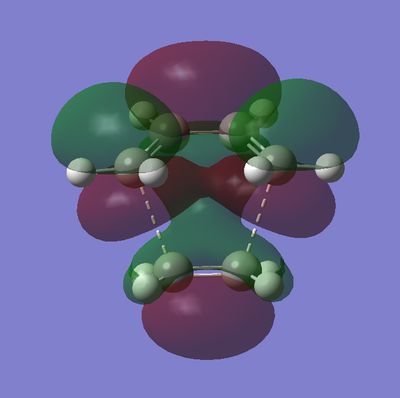
Energy / a.u	-0.21896	-0.00861
Symmetry	Anti-Symmetric	Symmetric

As described earlier in the analysis of the molecular orbitals of the reactants, it can be seen that the HOMO state in the TS derives from the overlap of the HOMO of cis-butadiene and the LUMO of ethylene. This particular interaction describes the σ-orbital interactions of the two single C-C bonds that are formed in this pericyclic process.

Similarly the LUMO of the transition state derives from the overlap of the LUMO of cis-butadiene and the HOMO of ethylene, resulting in the σ*-antibonding orbital interaction between the two aforementioned single C-C bonds.

Both of these observations results, very elegantly, from the conversation of orbital symmetry. This law states that the symmetry of an orbital formed by the overlap of two orbitals must be the same as the symmetry as the initial orbitals. Furthermore the symmetry of the two orbitals overlapping to produce the resulting orbital must also be the same.

The above observation is also in concordance with what would be expected from MO theory, which states that occupied orbitals may only interact with unoccupied orbitals, which is the case here.

Activation Energy of the Reaction

The reactants were optimized to the DFT - B3LYP/6-31G(d) level of theory using the following command:

#opt b3lyp/6-31g(d) geom=connectivity 

The resulting energies were -155.99594964 a.u. for cis-butadiene and -78.52266719 a.u. for ethylene. The sum of these two energies is -234.52861683 a.u. The energy of the TS is -234.54389655 a.u and hence the activation energy for this reaction is 0.01527972 a.u (40.1169 kJ/mol). This result is in satisfactory agreement with the literature value of 115 ± 8 kJ mol^-1 at 0K. This result may be further improved through the use of a more thorough basis set for all components.