Rep:Mod:slippynipps

Introduction and Aims

Nicholas Browning

This small project is an investigation into modelling of organic structure and reactivity. Such modelling allows great insight into the mechanistic detail of a reaction and allows the outcome of such reaction to be rationalised. This project makes use of two methods of calculation; molecular mechanics(MM2 and MMFP2 calculations), and semi-empirical molecular orbital modelling(PM6 calculations).

Modeling using Molecular Mechanics

Hydrogenation of Cyclopentadiene Dimer

Dimerisation

The dimerisation of cyclopentadiene proceeds via a [4π+2π] Diels-Alder cycloaddition. There are two possible stereoisomers formed fom this reaction and they are given the term exo or endo. The reaction proceeds via an aromatic transition state, and hence the reaction is very effective.

The relative stabilities of each isomer were modelled using the MM2 method. The following table presents these results.

Total energy for cyclopentadiene dimers (1 and 2)

	Molecule 1 (Exo)	Molecule 2 (Endo)
	exo	endo
Energy kcal/mol	31.8765	33.9975

The exo product is lower in energy, and hence is more stable; It is the thermodynamic product. However the endo product is formed predominantly even though it is higher in energy; it is the Kinetic product. The endo product forms faster than the exo product because it's reaction coordinate proceeds via a lower energy transition state due to a Secondary Oribtal Interaction between the p_z orbitals. This stereoselectivity was the fundamental basis ofAlder's endo rule.

Hydrogenation

The hydrogenation of the endo product (Molecule 2) produces two regioisomers (Molecules 3, 4) obtained through a reaction at one of the two available C=C double bonds. Both compounds were modelled and their energies calculated to determine the most stable product, and hence whether the hydrogenation is kinetically or thermodynamically controlled.

Taken from the Mod:Organic Page

Calculated energies for Molecules(3 and 4)

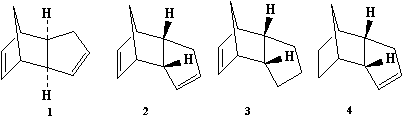
Energies (kcal/mol)	Molecule 3	Molecule 4
Stretch	1.2784	1.0968
Bend	19.8572	14.5236
Stretch-Bend	-0.8342	-0.5495
Torsion	10.8125	12.4970
Non-1,4 VDW	-1.2232	-1.0695
1,4 VDW	5.6322	4.5130
Dipole/Dipole	0.1621	0.1406
Total Energy	35.6850	31.1520

Molecule 4 is the more stable regioisomer, with an energy of 31 kcal/mol compared to 36 kcal/mol for molecule 3. Molecule 4 is the thermodynamic product. The large difference in energy between these regioisomers is due to the differences in bending energy; 19.9 kcal/mol for Molecule 3 and 14.5 kcal/mol for Molecule 4. This is difference is caused by the norborene C=C bond in Molecule 3, creating the greater ring strain imposed by the bridging methylene group. The cyclopentene ring does not have this ring strain and so upon hydrogenation there would be no release of steric repulsion. Hence the norborene C=C double bond is more easily hydrogenated than the cyclopentene double bond.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

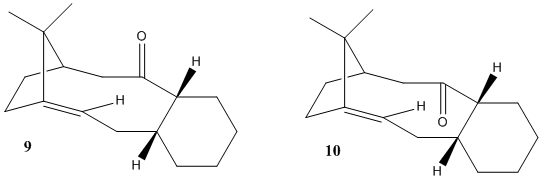
Molecules 9 and 10 are important intermediates in the synthesis of Taxol. Molecule 9 and 10 are atropisomers - isomers that arise from a restricted rotation about a single bond, which is usually caused by steric demand. The atropisomerism here is caused by a restricted rotation of the -C(O)- bond such that the carbonyl group points up or down. Molecule 9 has the carbonyl pointing down relative to the plane of the molecule, whereas molecule 10 has the carbonyl pointing up. It has been found by Elmore and Paquette that on standing molecule 9 isomerises to molecule 10 .

Taken from Mod:Organic Page

The energies of the atropisomers were calculated with the MM2 method, followed by the MMFF94 method for comparison.

MM2 calculated energies for imtermediate isomers (9 and 10)

Energies (kcal/mol)	Molecule 9	Molecule 10
	Taxol(up carbonyl)	Taxol (down carbonyl)
Stretch	2.7850	2.6209
Bend	16.5433	11.3386
Stretch-Bend	0.4304	0.3433
Torsion	18.2538	19.6685
Non-1,4 VDW	-1.5572	-2.1578
1,4 VDW	13.1092	12.8716
Dipole/Dipole	-1.7249	-2.0022
Total Energy	47.8396	42.6830
Total Energy (MMFF94)	70.5402	60.5643

Atropisomer 10 is the most stable isomer, having an energy of 42.7kcal/mol, comparitively to molecule 9 which has an energy of 47.8 kcal/mol. The difference in this energy is mostly due to the bending and torsional modes. The bending mode of Molecule 9 is 16.54 kcal/mol, ~ 5kcal higher than that of molecule 10. This results from there being two endo rings in molecule 9, increasing the amount of conformational strain. In Molecule 10 one is endo and the other is exo, resulting in less significant steric crowding. The torsional strain is likely due to the repulsive interaction between the carbonyl and the bridging iso-propyl group. These groups are further away in molecule 10 than they are in molecule 9, and hence the torsional strain is less. As a result of these two effects, molecule 9 will spontaneously isomerize to molecule 10.

The MMFF92 method shows that like in the MM2 method, molecule 10 is lower in energy than molecule 9. These energies however are higher than those produced by the MM2 method, but this is simply due to the different force field being applied.

Molecules 9 and 10 both react slower to hydrogenation than expected for strained alkenes (e.g see Cyclopentadiene Hydrogenation) due to a stability gained by the alkene possessing a caged structure.This is an example of a hyperstable alkene, which are less strained than their saturated forms and so have a lower reactivity than expected. This is due to the bridgehead location of the double bonds . A twisted olefin has a reduced π-overlap, resulting in an increase of the HOMO energy and a decrease of the LUMO energy. The HOMO-LUMO degeneracy is reached when the twist angle becomes 90^o and D_2d symmetry. They are characterized as having a negative "olefin-strain" energy, which is defined as the difference between the strain energy of an olefin and that of it's saturated parent ..

Modeling Using Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene to 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene

Electrophilic addition of dicholorcarbene to 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene(Compound 12) shows π-regioselectivity, specifically toward the syn alkene, with the anti alkene not being observed. .

Reaction of Compound 12 with dichlorocarbene

This regioselectivity is defined by molecular orbital interactions, specifically those in the region of the HOMO and LUMO. These molecular orbitals have been calculated using the PM6 method and are presented below.

Significant Molecular Orbitals of Molecule 12

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2
xy plane	xy plane	xy plane	xz plane	xy plane

It is clear that the syn-alkene is the HOMO orbital, whereas the anti-alkene is the HOMO-1 orbital. The HOMO orbital is a better electron donor due to being higher in energy and as a result it is much more nucleophilic than the anti-alkene. Therefore the electropihilic dichlorocarbene molecule is more likely to attack at the syn-alkene than it is at the anti-alkene. Further analysis of the energy diagrams shows the LUMO+1 represents the low energy C-Cl σ* orbital, and will interact with the high-energy anti alkene π orbital creating a stabilising antiperiplanar interaction, which subsequently lowers the energy of the anti-alkene π orbital, further retarding the ability of an electrophile to attack at the anti position. Resultantly any elecrophile strong enough to react at the anti-alkene would also attack the syn position, which explains why no anti-alkene is isolated in this reaction.

Vibrational Spectra

The influence of the Cl-C bond upon vibrational frequencies may be calculated using a B3LYP/6-31G(d,p) Gaussian optimised geometry and frequency calculation. In this calculation molecule 12 was compared to that of it's hydrogenated anti-alkene derivative. The results obtained are shown below.

tetrahydronapthelene derivative C=C and C-Cl stretching frequencies (cm^-1)

Derivative	C-Cl stretch	Anti-alkene stretch	Syn-alkene stretch
Molecule 12	771	1737	1757
Hydrogenated Molecule 12 (syn-alkene)	775		1758
Hydroxy group added	765	1753	1758
Silyl group added	764	1690	1756
Cyano group added	766	1706	1757

Firs tit should be noted that both the di-alkene and the hydrogenated mono-alkene belong to the Cs symmetry point group and so they both possess a plane of symmetry perpendicular to the principle axis of rotation (σv).

The C-Cl stretching frequency (770cm^-1) corresponds well to the literature value of 760cm^-1. However this is not true for the C=C bonds, which are significantly higher than those found in the literacture (1680cm^-1), suggesting that the C=C bonds in this calculation are slightly inaccurate. This is understandable, since this calculation does not take into account non-idealities such as solvent influence which perturb the harmonic nature of the vibrations and create anharmonic systems. The calculation also uses a simplified basis set which is much less accurate than a full basis set, however for the purpose of this exercise a full basis set was not possible in the time-frame and resources allocated.

The frequencies of the syn-alkene stretches are higher than those found for the anti-alkene which suggests the anti alkene has a lower bond energy and is therefore less stable. Although this somewhat contradicts the arguments made above, one must concider that both sigma and pi bonds contribute to the vibrational stretch. The argument made previously only discussed the influence of the π bond upon selectivity, and the anti-alkene can still retain a lower energy pi bond (hence less capable electrophilic attack by the dichlorocarbene) while also retaining a lower energy vibrational stretch through the effect of the σ-bond.

The stretching frequency of the syn-alkene in all derivatives of Molecule 12 does not change. This suggests that the anti-alkene does not affect the strength of the syn C=C bond. Upon adding substituents to the anti-alkene, it was found that the C=C and C-Cl stretching frequencies were changed substantially. The addition of the silyl group lowered the frequency the most, most probably through a back-bonding like donation of the π electrons into available Si d-orbitals, thus weakening the C=C bond. The addition of the cyano group also lowers the frequency by a reasonable amount, which is likely due to an inductive withdrawal effect removing electron density in the C=C bond. When the hydroxy group is added to the alkene, a higher C=C stretching frequency is observed due to the hyoxyl being more effective in resonance donation than inductive withdrawl,hence overall pushing electron density into the C=C π* orbital, thus strengthening the C=C bond and raising the frequency.

Glycosidation

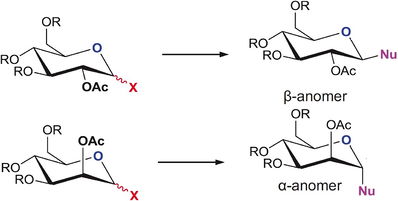
Fischer Glycosidation is the process by which an -OH group present on the anomeric carbon can be substituted for an -OR ester through the use of excess alcohol ROH in the presence of acid. This reaction is fundamental to carbohydrate chemistry as it is very useful for functional group interconversions and also for polymerisation of simple sugars. The unusual stereoselectivity of substitution observed is caused by the anomeric effect - a steroelectronic effect whereby the ring oxygen can donate a lone pair to the lowlying C-O sigma* orbital, effectively lowering the energy of that bond. This effect is most pronounced for the axial OR groups, as this allows for greatest antiperiplanar overlap and hence the major product of most glycosidation reactions is the alpha anomer.

However, If an -OAc group is located directly adjacent to the alpha anomer another effect is seen; one of regioselectivity, called the neighbouring group effect. In this section the effect of NPG upon the stabilities of different anomers is analysed, and hence a description of their stero and regioselectivity can be obtained.

Reaction Mechanism for α/ β Glycosidation anomers (Taken from the Mod:Organic Page)	Neighboring group effect (Taken from the Mod:Organic Page)

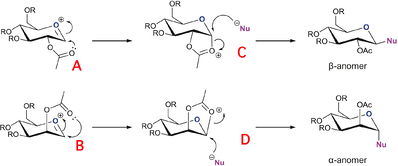
Molecules A and B exist in two forms, each having the -OAc carbonyl pointing above or below the ring, A , B and A', B' respectively. The intermediate products C and D showing neighbouring group effects have also been found to show this stereo-isomerism, and these are labelled C' and D'. In this calculation all molecules have been modelled using H as the R group, which provides minimal calculation time through low molecular bulk, hence minimising the number of conformations accessible.

First each compound was minimized in energy using the MM2 method, followed by a MOPAC/PM6 calculation to determine the heat of formation. This data is tabulated below.

MM2 calculated energies for imtermediate isomers (9 and 10)

Energies (kcal/mol)	Molecule A	Molecule A'	Molecule B	Molecule B'	Molecule C	Molecule C'	Molecule D	Molecule D'
	Taxol(up carbonyl)	Taxol (down carbonyl)	Taxol (down carbonyl)	Taxol (down carbonyl)	Taxol(up carbonyl)	Taxol (down carbonyl)	Taxol (down carbonyl)	Taxol (down carbonyl)
Stretch	1.4838	1.7168	1.7532	1.4553	1.5142	0.9042	0.9207	1.5401
Bend	6.5726	7.5929	6.9192	6.1247	14.8429	10.4009	15.6270	17.0251
Stretch-Bend	0.5248	0.6348	0.5506	0.4850	0.4209	0.2747	0.3131	0.4078
Torsion	1.4373	0.6508	1.0029	-0.0925	6.9599	6.7978	6.6988	6.1064
Non-1,4 VDW	-4.2604	1.5015	0.5677	-1.4042	-2.4432	-2.0862	-2.7026	-3.3041
1,4 VDW	11.2337	10.8786	11.2849	11.2644	11.1226	9.8603	9.9329	10.9250
Charge/Dipole	0.4252	-21.7256	-19.2916	-7.0876	0.2441	-9.6555	-8.8778	-6.5277
Dipole/Dipole	2.1893	4.2434	2.3366	2.7919	-2.8532	-3.4196	-5.2676	-3.5580
Total Energy (MM2)	19.6063	5.4931	5.1236	13.5371	29.8082	13.0766	16.6445	22.6147
Heat Of Formation (PM6)	-87.8797	-95.9676	-94.1989	-80.6763	-70.5416	-95.9665	-94.2014	-73.6995

From this table the following conclusions can be made.

A' is lower than A primarily due to contributions from Charge/Dipole. This is due to the favourable interaction between the δ- on the acyl carbonyl and the positively charged oxonium ion. In A this is energy is not favourable, due to the large differences between the charge and dipole. The same argument applies for why B is lower in energy than B'. This trend is also seen in the PM6 calculation. B is lower in energy than A'. Although the difference between A' and B total energies is small. This energy difference is not simply due to one factor, as both have similar steric strains/diaxial compressions, similar dipole/dipole and charge-dipole interactions. What seems to win out is the lower energy bending mode in B'.

Mini Project

Assigning regioisomers in "Click Chemistry"

Click Chemistry was formulated by Sharpless, K. B . It's general philosophy was based on those often present in biological reactions; adjoining small molecules together to create larger products. It is a philosophy for organic synthesis tailored in creating biological like reactions for joining small units together quickly and efficiently to form one larger product. The general concept of click chemistry is that it mimics nature. In order for a reaction to be defined as a "Click reaction" it must have traits similar to those listed below.

The reactions in Click Chemistry must:

• be modular in design

• be widely applicable
• produce very high yields
• show a large thermodynamic driving force
• generate non-toxic and easily removable byproducts
• be sterospecific
• be physiologically stable

The process in the aforementioned reaction must:

• have uncomplicated reaction conditions
• use simple, readily availible starting materials
• use a solvent that is easily removed, or not use one at all
• provide simple product isolation (e.g distillation)

The example that we will use in this project is the Azide Alkyne Huisgen Cycloaddition which was developed by Rolf Huisgen. This reaction was recently found to be accelerated in the presence of a Cu (I) catalyst, which gives specitic selectivity to the 1,4 isomer. The reaction stereospecifically prefers the 1,5 isomer when in the present of an Ru(II) catalyst. In this investigation the R groups will be defined as R¹ = -CH₂Ph and R² = -Ph

Click Chemistry Overall Mechanism	Products A & B

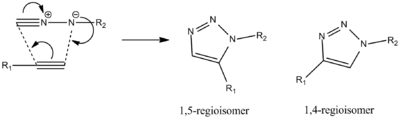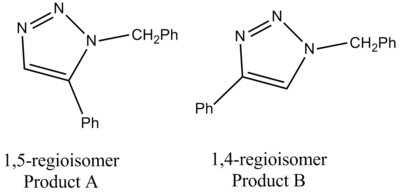MM2 Calculations

An MM2 calculation was used to minimised the energy for both isomers. This data is tabulated below.

MM2 calculated energies for Products (A and B)

Energies (kcal/mol)	Product A	Product B
Optimized Geometries:	Taxol(up carbonyl)	Taxol (down carbonyl)
Stretch	1.1514	0.7742
Bend	17.0751	13.1047
Stretch-Bend	0.0737	-0.0298
Torsion	-15.7474	-14.8274
Non-1,4 VDW	1.4209	-1.6827
1,4 VDW	14.8387	14.7239
Dipole/Dipole	-1.4831	-1.4079
Total Energy	17.3294	10.6550
Total Energy (PM6)	107.24755	107.75990

NMR

First the energy was minimized using SCAN for both isomers to produce lowest energy conformations. The resulting file was then resubmitted for NMR calculations.

Product A

NMR Spectra of Product A DOI:10042/to-11810

13C NMR Spectrum

1H NMR Spectrum

15N NMR Spectrum

Product A C¹³ Assignment

¹³C NMR for Product A

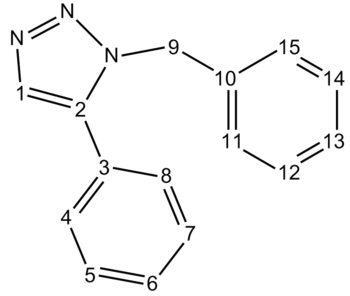
Carbon	Gaussian Calculated Shift (ppm)	Literature Shift (ppm)	Integeration
1	128.63	133.34	1
2	136.67	138.28	1
3, 13	124.69,124.47	128.22	2
4	126.23	133.26	1
5, 8, 14	125.61, 125.49	129.08	3
6	125.87	129.64	1
7, 12	125.20 , 125.06	128.92	2
9	52.24	51.85	1
10	134.10	135.66	1
11	123.39	126.93	1
15	123.66	127.22	1

Product B

NMR Spectra of Product B DOI:10042/to-11811

13C NMR Spectrum

1H NMR Spectrum

15N NMR Spectrum

Product B C¹³ Assignment

¹³C NMR for Product B

Carbon	Gaussian Calculated Shift (ppm)	Literature Shift (ppm)	Integeration
1	117.75	120.00	1
2	146.30	148.60	1
3	126.82	130.90	1
4	123.18	128.40	1
5, 7	126.10,126.20	129.20	2
6, 15	125.48,	128.50	2
8	122.58	126.10	1
9	56.11	54.60	1
10	134.37	135.10	1
11, 12, 13	126.10, 125.80	129.10	3
14	126.50	129.50	1

NMR Analysis

The NMR data produced from the calculation fit the literature data well. The values obtained are lower than those listed in the literature, which could be due to solvent influencd deshielding. Despite this, the calculations are very accurate in NMR prediction.

The key to determinig between the two isomers seems to be the phenyl-substituted alkene within the tri-azole ring, environment 1 & 2 in Product A and B. Isomer A shows the phenyl-substituted carbon peak (environment 2) at 136 ppm whereas isomer B shows it at 146 ppm.This is likely due to the coplanar phenyl group in B increasing the ring current in the tri-azole ring and hence increasing the amount of deshielding present at that carbon. In Isomer A this phenyl group is not coplanar, and hence overlap between the π-orbitals of the two ring systems is less profound. Similarly the hydrogen bearing carbon peak( environment 1) has a ppm value of 128ppm in Product A and 117.75 ppm in product B. Apart from these two peaks, other peaks tend to be very similar and hence are not particularly useful to discern between the two isomers.

Hypothesis Testing

Next we compare an unassigned spectrum of Product B from a different source . The literure values are: ¹³C NMR(101 MHz, CDCl₃) δ = 148.4, 134.9, 130.8, 129.4, 129.0, 129.0, 128.4, 128.3, 125.9, 119.8, 54.4. Here we can see both values highlighted earlier present in this spectrum, that of 148.4 and 119.8 which very neatly correspond to those obtained by the calculation for product B. Clearly it is both possible and facile to use calculated NMR spectra to discern between real regioisomeric products.

Vibrational Spectra

Vibrational Spectra of Product A and B

Product A DOI:10042/to-11893	Product B DOI:10042/to-11892

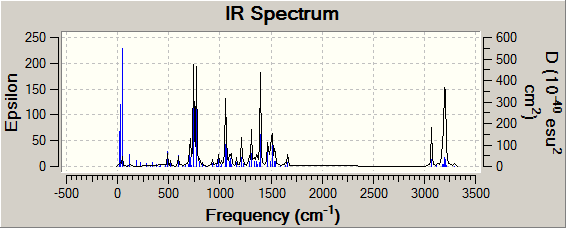The two spectra are very similar. This is not a good tool for regioisomeric distinction because if any theorem were to be created to analyse which regioisomer had been formed, they are likely to be invalidated by the influence of solvent type/concentration.

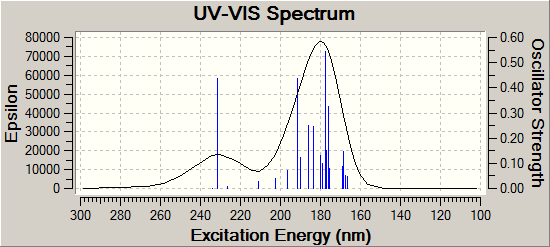
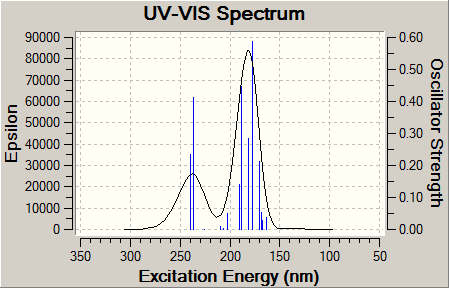
UV-Vis spectrum

UV-Vis Spectra of Product A and B

Product A DOI:10042/to-11896	Product B DOI:10042/to-11897

Both UV-Vis spectra are similar, with both products producing two large peaks in similar regions. For product A these peaks occur at 231.0nm and 178.6nm whereas the corresponding peaks occur at 237.8nm and 180.2nm for Product B. It would be difficult to tell the isomers apart purely on the basis of UV-Vis alone, which is understandable simple both have similar π-systems, and hence similarly accessible electronic energy levels.

Optical Rotation

Product A: [Alpha] (5890.0A) = -45.10 deg DOI:10042/to-11894 Product B: [Alpha] 5890.0A) = 92.78 deg DOI:10042/to-11895

The calculation for Optical Rotation is likely to be in increasing error for any rotation below 100 Degrees. Here we see that Product A is well below 100 degrees and hence is very much likely to be incorrect. Product B however may still be close to it's real value.

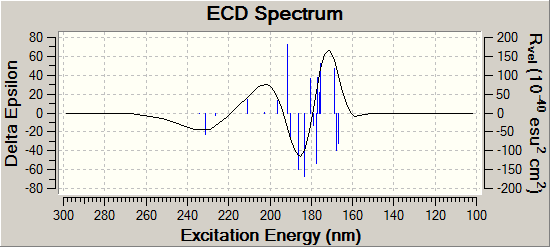
CD-Spectrum

CD Spectra of Product A and B

Product A DOI:10042/to-11896	Product B DOI:10042/to-11897

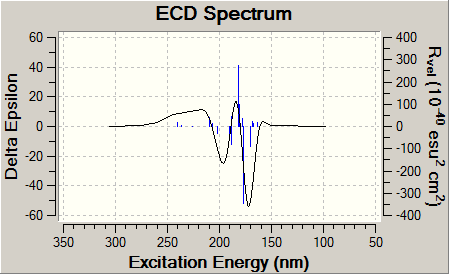
Here we can see a clear distinction between both CD spectra. For product A the three peaks occur at 173.2nm, 184.8nm, 197.2nm and have values 63.8R_vel,-45.2R_vel, 20.5R_vel respectively. For product B these peaks occur at 173.6nm, 183.2nm, 194.0nm and have values -50.8_vel, 16.2_vel, -22.1_vel respectively. Clearly Product B is the vertically flipped version of Product A in terms of spectra, and this would serve as a very simple but powerful technique to discern between the two regioisomers.

Conclusion

This mini project has proven it is simple to determine between the regioisomers using calculated spectroscopic data. Two powerful techniques have emerged from the project in this aspect, that of ¹³C NMR providing the key to identification through the tri-azole alkene shifts, and also the sign of the peaks present in the CD spectrum. The calculated UV-Vis did not provide any insight into identification, simply due to the similarity of the π-systems present in both molecules. Similarly Vibrational Spectroscopy provided little insight due to both molecules sharing the same functional groups, and as a result only small differences in peak values were noticed.

Naturally it is wise to conciser the chemical reaction in question, and it's products, in order to determine which spectroscopic techniques will best allow distinction between products.