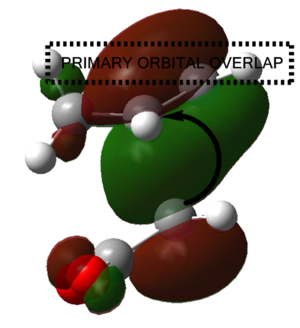
Rep:Mod:slau1991
Computational Labs
Samantha Lau
Introduction
Computational chemistry allows us to be severely frustrated in ways not known to man before, with calculation errors popping up immediately or worst after a 15minute run. In reality the convenience and accuracy of computational software such as Gaussian leaves us crawling back for more torture as it allows us to simulate molecular reactions in mere seconds and analyse the molecular oribtals of HOMO-LUMO interactions to predict the success or failure of certain reaction pathways. The importance of computational chemistry is growing, it allows us to perform dangerous chemical reactions in the comfort of our laptops without ever having to touch poisonous chemicals (not that this is a positive for some chemists out there).
In this experiment we will be using molecular mechanics and semi-empirical methods in order to probe our systems. Molecular mechanics are used for simple energy functions which are quick to solve so are cheap to compute. The calculations are based on force field information so the anharmonic oscillator parameters are enforced where bonds are treated like springs and the actual atoms are treated like balls on these springs. The cons of using molecular mechanics is when used for electronic interactions of bond forming-breaking transition states as there is no unique function for each energy term with number of parameters rising rapidly for non CHNO elements. Semi empirical methods uses both classical and quantum mechanics for approximations to simplify the Schrödinger equation therefore can be used for calculations concerning electronic interactions and bond forming-breaking transition structure [1].
Pericyclic reaction involving sigmatropic shift and cycloaddition will be explored to see how Gaussian is able to replicate experimental with theoretical calculations using the above methods. The HOMO-LUMO orbitals will be analysed to understand allowed and forbidden transition states of such reactions.
Module 3
Cope rearrangement
1,5-Hexadiene: Optimising reactants and products
In this part of the experiment Gaussview software will be used in order to optimise molecules, run frequency analysis to compare potential energies of the starting material and view vibrational modes of the molecules in question. The [3,3] sigmatropic shift of 1,5-Hexadiene will be studied in detail to appreciate the pericyclic reaction and the transition states which the molecules goes through during the concerted rearrangement of the sigma bond depending on the starting configuration.
Hatree-Fock (HF) method will be used consistently in this experiment to determine the ground state wave function and therefore the ground state energy of a quantum system asumming that energy eigenfunction can be described by a single Slater determinant of orbitals. Variational principle is also employed in this methods which involves using a trial wavefunction under certain parameters and then finding the values of these parameters whereby the expectation value of the energy is the lowest.
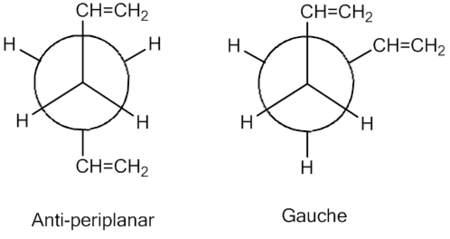
1,5 Hexadiene was drawn with the first arrangement being anti-periplanar for the central four C atoms. The following method at Hatree-Fock (HF) and basis set 3-21G level of theory was used to optimise the molecule. The memory was changed to 500MB under method tab and the newly crated input file was submitted for calculation. The chk. file was opened once optimisation was complete in order to see the preferred configuration of the anti-periplanar arrangement with the lowest energy value from the drawn configuration.
The same procedure with the same level of theory was performed on the other anti-periplanar and gauche configuration of 1,5 hexadiene yielding the following results:
| Conformer | Point Group | Energies /Hartrees |
Relative Energies /kcalmol-1 |
| Antiperiplanar 1 | C2 | -231.69260237 | 0.04 |
| Antiperiplanar 2 | Ci | -231.69253530 | 0.08 |
| Antiperiplanar 3 | C2h | -231.68907062 | 2.25 |
| Antiperiplanar 4 | C1 | -231.69097054 | 1.06 |
| Gauche 1 | C2 | -231.68771615 | 3.10 |
| Gauche 2 | C2 | -231.69166702 | 0.62 |
| Gauche 3 | C1 | -231.69266122 | 0.00 |
| Gauche 4 | C2 | -231.69153036 | 0.71 |
| Gauche 5 | C1 | -231.68961575 | 1.91 |
| Gauche 6 | C1 | -231.68916018 | 2.20 |
1 hartree=627.509kcalmol-1
The lowest energy configurations calculated under the HF/3-21G level of theory are gauche 3, anti-periplanar 1 and 2 in the following order. Without having used Gaussview to calculate these energies so from observation alone one would have hypothesised the lowest configuration to be anti-periplanar 1 or 2 with the CH=CH2 groups pointing away from each other as far as possible as well as away from carbon 3 and 4 with their hydrogens so sterically most favoured to avoid clashing of the CH=CH2 with any other part of the molecule. However Gaussian has predicted the lowest energy configuration to be gauche 3 with initially what seems to be unfavoured clashing of both CH=CH2 groups. The low energy may be attributed to the π orbital of the alkene group having an attractive interaction with the hydrogen on the other alkene group[2] however molecular orbital analysis will have to be performed to see these interaction but one can stipulate this for the reason gauche is favoured over the anti-periplanar configurations. For gauche 1, 5 and 6 there is unfavourable clashing of the hydrogens on the alkene groups resulting in a higher relative energy than the other conformers. The short central bond of antiperiplanar 3 (1.53Å) and antiperiplanr 4 (1.54Å) can explain the high relative energy from the clashing of the hydrogens in the central C-C bond leading to unfavourable energies.
Now using a higher level theory of DFT B3LYP/6-31G* the 3 lowest energy configurations shown above was re-optimised yielding the following results.
| Conformer | Point Group | Energies /Hartrees |
Relative Energies /kcalmol-1 |
| Antiperiplanar 1 | C2 | -234.61179055 | 0.00 |
| Antiperiplanar 2 | Ci | -234.61171035 | 0.05 |
| Gauche 3 | C1 | -234.61132934 | 0.29 |
Using a higher basis set the lowest energy configuration is now anti periplanar 1 however the energy difference between antiperiplanar 2 and gauche 3 is incredibly small as shown by the relative energies. Using density function theory (DFT) allows calculations to be made using more wavefunctions which in this case is spatially dependent on electron density however one should not directly compare absolute energies calculated using different basis set as the calculations to determine the energies are based on different factors. What we can take a look at are the difference in geometry between the structures from the two different basis set.
| Antiperiplanar 1 | Antiperiplanar 2 | Gauche 3 | ||||
| HF/3-21G | DFT/B3LYP 6-31G | HF/3-21G | DFT/B3LYP 6-31G | HF/3-21G | DFT/B3LYP 6-31G | |
| C=C/Å | 1.32 | 1.33 | 1.32 | 1.33 | 1.32 | 1.33 |
| C-C/Å | 1.51; 1.55 | 1.50; 1.55 | 1.51; 1.55 | 1.50; 1.55 | 1.51; 1.55 | 1.50; 1.55 |
| Bond Angle/° | 124.8; 111.4 | 125.3; 112.7 | 124.8; 111.3 | 125.3; 112.7 | 124.5; 125.0; 111.9 | 124.9; 125.5; 113.5 |
| Dihedral Angle/° | 176.9 | 176.7 | 180.0 | 180.0 | 67.7 | 66.3 |

Comparing the conformers using the same basis set HF/3-21G we can see the bond lengths of the C-C and C=C bonds are pretty similar with the major difference being the dihedral angle of the central C-C-C-C framework. The dihedral angle of the reference gauche conformer would be 60° but as calculated for the lowest conformer under this basis set is slightly larger at 67.7° which lowers torsional strain with the CH=CH2 groups further away from each other. Using HF/3-21G the calculations doesn't take into account any of the electronic considerations and therefore any favourable CH-π interactions which would explain the change in ordering under the higher basis set of DFT/6-31G. What can be said definitively without having performed molecular orbital analysis on the molecules is that slight changes to the dihedral angle and depending on which basis set is used, the antiperiplanar and gauche conformation of 1,5-hexadiene are very similar in energies and the margin of error in the calculation can account towards the change in energy order. Therefore speculation is not advisable [3] when understanding the ordering of the conformation except that they are incredibly close in energies.
| Antiperiplanar 1 | Antiperiplanar 2 | Gauche 3 | ||||
| HF/3-21G | DFT/B3LYP 6-31G | HF/3-21G | DFT/B3LYP 6-31G | HF/3-21G | DFT/B3LYP 6-31G | |
| E = Eelec + ZPE (0K) | -231.539601 | -234.469298 | -231.539540 | -234.469204 | -231.539486 | -234.468693 |
| E = Eelec + Evib + Erot + Etrans (298.15K) | -231.532645 | -234.461966 | -231.532566 | -234.461857 | -231.532647 | -234.461464 |
| H = E + RT | -231.531701 | -234.461022 | -231.531622 | -234.460913 | -231.531703 | -234.460520 |
| G = H - TS | -231.570954 | -234.500862 | -231.570914 | -234.500777 | -231.570640 | -234.500105 |
The following thermochemistry data is obtained for the three lowest energy configurations of 1,5-hexadiene at the two different basis set levels. The sum of the electronic and zero point energy is the potential energy at 0K, the second energy is calculated at 298.15K and 1 atm and is the the energy from vibrational, rotational and translational modes (thermal energies) and electronic energy. The third energy is important when looking at dissociation reactions as it's the additional correction for RT for thermal enthalpies. The fourth energy includes the entropic contribution to the thermal free energy (G).
There is a large difference of ~3 Hatree between the energies obtained for the two different level basis set, again this doesn't mean one result is better than the other as they cannot be compared directly. Instead we will just look in depth at the DFT/B3LYP 6-31G level of theory as it takes into account electronic interactions. The trend of the energies between each conformer is in agreement with the results obtained from the lowest conformation energy with antiperiplanar 1 conformer having the lowest energy for all 4 values from thermochemistry data then antiperiplanr 2 then gauche 3.
The zero point energy is the lowest energy that a system can have of its ground state, Gibbs free energy is a measure of useful work that can be obtained from the system and the enthalpy is a measure of the total energy of a thermodynamic system. With this in mind the optimisation and frequency calculation were ran again under the same conditions for the 3 different conformers however in additional keywords was inserted "0.00001K" (Gaussian unable to compute 0K) with the values for all the thermochemistry the same number as the sum of the electronic and zero point energy of each respective conformer. This makes sense as no vibrational rotational or translational energy is available at absolute zero with contribution only from the electronic properties of the system.
Optimising "Chair" and "Boat" transition states

The transition state (TS) of the cope rearrangement are the "boat" and "chair" transition states consisting of two C3H5 allyl fragments approximately 2.2Å apart. In order to optimise the TS structures one of the allyl fragements has to be optimised first using HF/3-21G level of theory yielding a molecule with C-C bond length 1.39Å and C-C-C bond angle of 124.3Å with symmetry point group C2V.
The optimised allyl fragment was reproduced twice into a new molecule window which was orientated to form the chair TS with the two fragments being roughly 2.2Å apart. The reference chair transition state will be optimised manually using two different methods.
For the boat transition state the starting material used was the optimised 1,5-hexadiene molecule in it's antiperiplanar 2 form in part one of the experiment using QST2 method.
Chair TS optimising to TS(Berny)

The initial method was to optimise to transition state which is only feasible if the geometry of the transition state structure is known and therefore the force constant matrix (Hessian) can be computed whereby the change in the structure of every bond in the molecule can be calculated individually which will be updated as the optimisation proceeds. The pre-built reference chair transition state structure calculation was set up to "Opt+Freq" with optimisation changed to a TS(Berny) and force constants chosen to be calculated once and in additional keywords "opt=NoEigen" was inserted to ensure the calculation continues without crashing if more than one imaginary frequency is detected during the optimisation and frequency analysis. The HF/3-21G level of theory was used again as well. The imaginary frequency is of magnitude 818cm-1 with the animated vibration corresponding to the Cope rearrangement with C-C bond length between the terminal allyl fragments being 2.02Å and C-C-C bond angle of 101.9°
Chair TS optimising to a minimum

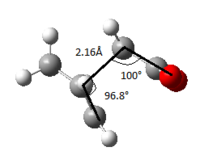
Optimising to a transition state is harder than optimising to a minimum as the calculations needs to know where the negative direction of curvature is however as stated in the previous section, if the TS is known then a reasonable guess can be made. This second method generates a transition structure by freezing the reaction co-ordinates (terminal carbons where the bond breaks and forms) and minimising the rest of the molecule. Once the molecule is relaxed the reaction co-ordinates are unfrozen and the optimisation of TS is started again. This calculation is different to using force constants as it only calculates the force constant at the reaction co-ordinates rather than the whole molecule which saves a considerable amount of time for calculation but of course is less accurate. For a molecule this size this method gives a good enough initial force constant matrix. Once again the HF/3-21G level of theory was used with the calculation set to "Opt+Freq" with the optimisation set to a minimum and in additional keywords inserted "Opt=ModRedundant" which calculates just the force constants of the frozen reaction co-ordinates. The exact reaction co-ordinates were chosen initially before calculation set up by opening up the reference chair transition structure and from the "edit" menu choosing "redundant coord editor" which opens to a matrix table where we can select the bonds which we want to freeze from the molecule window. Once again the imaginary frequency generated is of the magnitude 777cm-1 with the animated vibration corresponding to the Cope rearrangement with C-C bond length between the terminal allyl fragments being 2.15Å and C-C-C bond angle of 100.2°
This molecule is once again optimised using the same method of selecting the specific bonds of the reaction co-ordinate however this time instead of selecting to freeze the reaction coordinate the "derivative" is chosen instead and the transition state optimised once again however with the force constant chosen to be calculated never. The imaginary frequency generated is of the magnitude 818cm-1 with the vibration once again corresponding to the Cope rearrangement with C-C bond length between the terminal allyl fragments being 2.02Å and C-C-C bond angle of 101.9°
Boat TS using QST2 optimisation
Again using the HF/3-21G level of theory the boat transition state was optimised using QST2 method. This method allows us to specify the reactants and the products for a reaction and Gaussian will interpolate between the two structures so that it can find the transition state between the two. The optimised 1,5-Hexadiene molecule corresponding to antiperiplanar 2 molecule calculated in part one of this experiment was used as the reactant and product of this rearrangement reaction. It was labelled in the same way as shown below in order for the calculation to be performed correctly. The two labelled hexadiene molecule were orientated as shown to mirror the arrow pushing mechanism of the reaction.
| Reactant | Product |
The calculation was set as "Opt+Freq" with optimisation selected to be TS(QST2) and submitted. However this lead to a failed job as the boat transition structure looked more like chair transition structure but more dissociated. This is because the calculation linearly interpolated the structure submitted rather than rotating around the central carbon bonds. Instead the rotation of the bonds were set manually to form the following structures depicted.
| Reactant | Product |
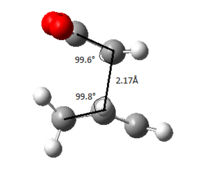
The same input calculation was run on the newly orientated molecules with the calculations converging towards a boat transition structure. The imaginary frequency magnitude calculated was at 840cm-1 with the C-C bond length between the terminal allyl fragments being 2.14Å and C-C-C bond angle of 103.4°.
Optimisation of Chair and Boat TS using DFT/B3LYP 6-31G*
Using the optimised files for both the chair and the boat TS from the HF/3-21G level of theory we re-optimised the molecules using a higher basis set with the density functional theory (DFT)/B3LYP 6-31G* running an "Opt+Freq" analysis keeping everything else the same as the before for the calculations for optimising the chair and boat TS.
We can compare the difference in geometries and energies of the TS between the two levels of theory yielding the following table:
| HF/3-21G | DFT/B3LYP 6-31G* | |||
| Chair TS | Boat TS | Chair TS | Boat TS | |
| Electronic energy | -231.619322 | -231.602802 | -234.556983 | -234.543093 |
| E = Eelec + ZPE | -231.466699 | -231.450928 | -234.414933 | -234.402339 |
| E = E + Evib + Erot + Etrans | -231.461339 | -231.445299 | -234.409011 | -234.396005 |
| H = E + RT | -231.460394 | -231.444354 | -234.408067 | -234.395061 |
| G = H - TS | -231.495206 | -231.479774 | -234.443818 | -234.431748 |
| terminal C-C/Å | 2.02 | 2.14 | 1.97 | 2.21 |
| C-C/Å | 1.39 | 1.38 | 1.41 | 1.39 |
| C-C-C-C/° | 54.8 | 0 | 54.0 | 0 |
| Imaginary Freq./cm-1 | 818 | 840 | 566 | 531 |
Comparing the electronic energies between the boat and the chair transition state within the same basis set we can see Gaussian has calculated chair to be the more stable transition state with a difference of 10.4kcalmol-1 for the HF method and 8.7kcalmol-1 for DFT method. The transition state of this pericyclic sigmatropic shift can be compared to cyclohexane as it adopts the boat and chair conformer as well as half chair and twist boat structures. What we can obtain from this comparison is that the chair conformer is also the most stable configuration of cyclohexane with the difference in energy between the chair and boat TS being 6.5kcalmol-1[4]. Looking at the geometry of the chair and boat TS the terminal C-C "bond" (where the bond forms and breaks) of the boat TS is longer than for chair; the distance of these terminal C-C bond lengths are longer than "normal" alkane single bonds of 1.52Å [5] but the greater distance of the distance between the terminal carbons makes it harder to form new new bonds. The C-C bonds within the alkyl fragments have bond lengths which are reasonably similar in magnitude between the two TS with the bonds being between a single (1.52Å [5]) and double carbon bond (1.30Å [6]) showing the delocalisation of the system with electron density being shifted around the structure to form the product of the pericyclic reaction.
What is interesting to notice is the huge difference in the magnitude of the imaginary frequency calculated between the level of theory between HF and DFT methods. The imaginary frequency corresponds to the formation and breaking of the single double bonds in the pericyclic reaction. The difference in energy using the different basis set on the same TS mimics the results seen for 1,5-hexadiene conformational analysis and once again we can't compare these energies as the basis set uses different parameters and factors to calculate energies.
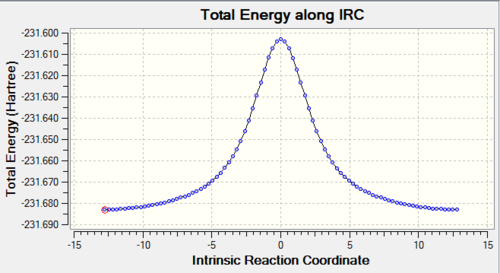
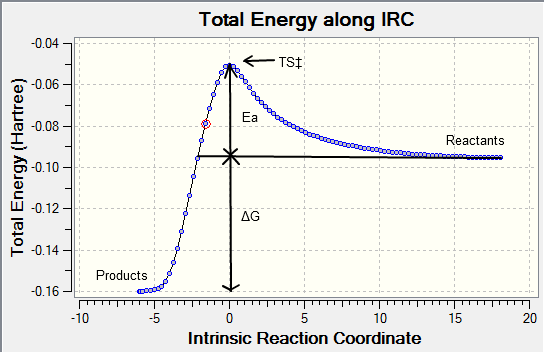
Intrinsic Reaction Coordinate (IRC)
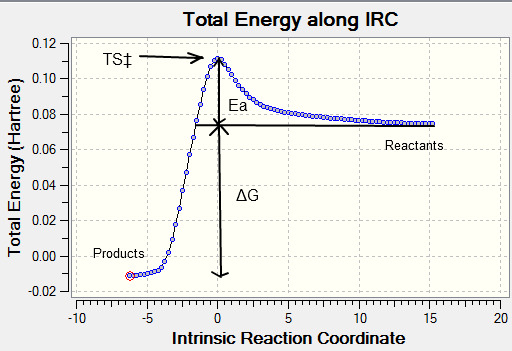
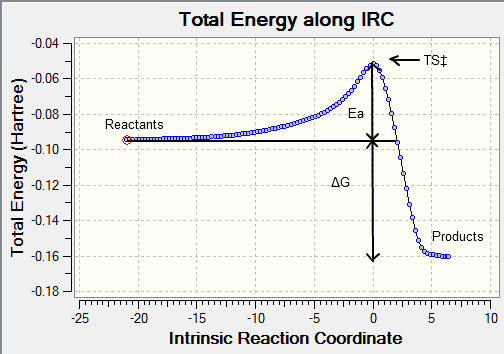
The IRC allows us to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface by creating a series of points by taking small geometry steps in the direction or slope of the energy surface where its at its steepest.
The optimised chair and boat structures were put through an IRC calculation where the reaction coordinate was calculated for both directions of the reaction (even though in this case the reaction coordinate is symmetrical) with the force constants chosen to be calculated always with the number of points considered along the IRC as 100 and then submitted yielding the following graphs:
| Boat IRC - 298.15K | Chair IRC - 298.15K |
| Boat - 298.15K | Chair - 298.15K |
The activation can be read straight from the graph yielding the following results summarised below:
| HF/3-21G | DFT/B3LYP 6-31G* | Expt.[7] | |||
| at 0K | at 298.15K | at 0K | at 298.15K | at 0K | |
| ΔE (Chair) | 50.3 | 45.3 | 33.7 | 33.7 | 33.5 ± 0.5 |
| ΔE (Boat) | 50.3 | 50.3 | 37.6 | 37.6 | 44.7 ± 2.0 |
The activation energy Ea is the difference between the transition state and reactant potential energy. It is the potential energy barrier which governs the amount of energy required for a system to complete its reaction and is best expressed by the Arrhenius equation : where where is the pre-exponential factor, is the universal gas constant (8.314JK-1) , is the temperature (K), and is the reaction rate constant. Therefore the activation energy is a kinetic property with the lower the potential barrier the faster the reaction can proceed. What we can conclude from this experiment is that the activation energy for the pericyclic reaction to occur via the chair transition state will occur at a faster rate than via the boat transition state, this is in agreement with the experimental trend. The chair activation energy calculated at the higher basis level lies very close to experimental value whereas at the HF lower basis set the value is marginally off. From this comparison we can suggest that DFT is a more accurate calculation than HF for this particular molecule and conformation. However the values calculated for the boat transition state at both level of theory is off from the experimental value so we cannot conclude which basis set is more accurate for the boat TS.
What is interesting though from these calculations is that at the higher DFT basis set method the activation energy values calculated at 0K and 298.15K is the same for the chair and boat conformer respectively which is mirrored for the boat conformer at the lower basis set as well. We can surmise that at two different temperatures the activation energy doesn't change drastically it seems with only the chair conformer calculated at the lower basis set showing greater deviation of activation energy at different temperature. But as stated the accuracy of this lower basis set isn't the greatest for this conformer.
The Diels Alder Cycloaddition
The Diels Alder cycloaddition is a well known pericyclic reaction whereby a new ring structure is formed from a concerted reaction between a diene and a dieneophile. The reaction like the Cope rearrangement occurs in a concerted manner with the diene having to be in a s-cis formation in order for the reaction to be allowed; this arrangement maximises HOMO-LUMO overlap however symmetric factors also needs to be considered to ensure the reaction is not forbidden.
The prototypical reaction between ethylene and cis form of butadiene will be studied to analyse the frontier orbital interactions and understand what happens during the transition state of the reaction. The butadiene contributes 4π electrons and the ethylene contributes 2π electrons so overall the system is classified as a [4π2 + 2πs].
The symmetry properties of the orbitals can be defined with respect to a plane of symmetry or an axis of symmetry. With this in mind we can obtain the HOMO-LUMO orbitals of the reactants from Gaussian and decide which symmetry they belong to and therefore view the allowed reaction paths.
cis 1,3-Butadiene and ethylene

Using semi-empirical/AM1 level of theory the inidvidual reactant molecules of butadiene and ethylene were optimised and then combined in a new molecule window, orientated ~2.2Å apart in the suggested envelope transition state structure to maximise orbital overlap of the HOMO-LUMO interactions. A "Freq+Opt" calculation was ran on the transition structure optimised to a TS Berny with the force constant calculated once. The imaginary frequency magnitude calculated was at 956cm-1 which corresponds to the cycloaddition reaction, the animation of this imaginary frequency can be found here. An interesting vibrational mode to take notice when comparing the imaginary frequency to the one of the lowest positive frequency of vibration found at 246cm-1 is that this mode of vibration corresponds to the asynchronous formation of the product with the vibrational mode showing one sigma bond forming after the other rather than at the same time, this vibrational mode can be viewed here.
We can analyse the HOMOs and LUMOs of the reactants to find the symmetry of them and then probe the allowed reaction paths.
| Cis butadiene | Ethylene | |||
| MO |  |
 |
 |
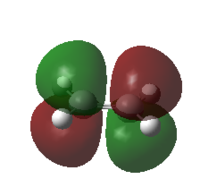
|
| HOMO | LUMO | HOMO | LUMO | |
| Symmetry | antisymmetric | symmetric | symmetric | antisymmetric |
| Energy/Hartree | -0.34384 | 0.01710 | -0.38776 | 0.05284 |
The symmetry calculated for the MOs are with respect to the reflection plane of symmetry and therefore we can suggest the HOMO-LUMO of both reactants interact i.e. symmetric with symmetric and antisymmetric with antisymmetric, leading to the product formation. With the reactants MOs on hand we can probe the MOs of the transition state of the reaction in order to see the satisfaction for the pericyclic selection rules[8]: under thermal conditions with the electron count 4n+2 (n=1) in this case the stereochemistry of the reaction should go via suprafacial (same face of one π system) route (or two antarafacial) to form a Hücklel transition state.
| TS MOs | ||
| MO |  |

|
| HOMO | LUMO | |
| Symmetry | antisymmetric | symmetric |
| Energy/Hartree | -0.32393 | 0.02315 |


Looking at the frontier molecular orbitals of the reactants and the product we can deduce the reacion path proceeded through the HOMO of the cis 1,3 butadiene and the LUMO of the ethylene as the HOMO of the transition state structure corresponds to the same antisymmetric symmetry with the overall stabilisation of the energy of the system. The reaction via the HOMO of the ethylene and the LUMO of the cis 1,3 butadiene was also accessible but as shown by the energy of the transition state MOs the other route is favoured as the MO is lower in energy.
However in order to confirm a transition state has been obtained from the optimisation calculation an IRC can be run to plot the reaction path and the energy of the system as it undergoes the change. Under the same molecular level of theory of "semi-empirical/AM1" an IRC was chosen to run both the forwards and backwards path with force constant chosen to be calculated "always" and the number of points taken to be 100. The IRC graph shows the maxima found during the reaction path which corresponds to the transition state of the reaction with the total number of points calculated on the graph to be 87. Looking at the geometry of the transition state the calculated bond lengths between the terminal C-C are also the same value (2.12Å) showing that the reaction is indeed concerted in fashion of the sigma bonds making at both ends simultaneously with one π bond overall in the final product which is the specification of a cycloaddition reaction. The general bond length of a single C-C bond is 1.54Å[5] and for a double C=C bond is 1.30Å[6]; the bond length between the two terminal fragments at 2.12Å is much longer than for single bond. The van der Waals radius of the C atom is calculated to be 1.70Å[9] therefore between the two carbon atoms the total distance of interaction is 2 x van der Waal interaction = 3.4Å which is within the length of the calculated transition state structure of the bond formation between the two carbon terminal fragments making the interaction between the two fragments attractive. The angle of approach of the ethylene molecule towards the cis 1,3 butadiene was calculated to be 99.3° which maximises the oribtal overlap of the HOMO-LUMO of the reactants as shown in the MO diagrams of the transition state structure. We can deduce that the transition state is closer to the reactants that it is to the product from this geometry analysis.
The calculated activation energy of the reaction is 23.2kcalmol-1 which is very close to literature value obtained (23.8kcalmol-1[10]). The magnitude of the Gibb's free energy of the reaction is 53.7kcalmol-1 with literature value obtained being 40.0kcalmol-1 [11], this reaction is exothermic with the reaction driven by the formation of a 6-membered ring structure and formation of two new sigma bonds (even at the expense of losing 2 pi bonds).
| IRC of prototypical Diels Alder reaction | Animation of reaction |
Maleic anhydride and cyclohexa-1,3 diene
The symmetry of the final product from the prototypical reaction of ethylene and cis-butadiene doesn't allow us to explore the regioselectivity of the cycloaddition reaction. Using maleic anyhydride and cyclohexa-1,3 diene opens up the exploration of whether the exo- or endo- conformer is preferred thermodynamically and kinetically.
The respective starting materials were drawn and optimised at semi-empirical/AM1 level of theory. The optimised molecules were then copied into a new molecule window and arranged in a guess transition state structure. An initial optimisation freezing the reaction co-ordinates was run to find a better guess transition state structure with the file found here for endo conformer and here for exo conformer. This was then put through an "Opt+Freq" calculation with the two different conformers optimised to a TS Berny state and force constant calculated once with "opt=noeigen" inserted into additional keywords.
The following table summarises the relative energies of the endo and exo conformer as well as some analysis on the geometry of the TS.


The relative energy of the transition state shows that the endo conformer has a more negative value than the exo conformer. The energies can be compared in this case as the same calculation method was used on the same number and type of atoms; this means that the endo conformer shows a greater stability than the exo conformer.
The geometry of the molecules are very similar with the terminal carbons between the fragments being within the van der Waal radius of two carbon atoms (3.40Å[9]) showing the interactions are attractive however for endo the bond length is slightly shorter than exo bond length. It would be inadvisable to compare such a small value due to margins of error associated with calculations even if the results does agree with theory. The actual C-C bonds involved in the Diels-Alder reaction show similar bond lengths and also between a single and double carbon carbon bond showing the aromaticity involved in the transition state with the delocalisation of the electrons during this concerted cycloaddition reaction.
The calculated magnitude of the imaginary frequencies correspond to the pericyclic reaction and once again the animation of these frequencies show the concerted fashion of the reaction and strengthens the argument that the two sigma bonds are formed synchronously. The endo vibrational mode can be viewed here and the exo vibration mode can be viewed here. At the transition state the length of the two terminal bonds at each end of the fragments are also the same length at 2.16Å and 2.17Å respectively for the endo and exo form as well to strengthen the synchronous argument stated previously.
| Cyclohexa1,3 diene | Maleic Anhydride | |||
| MO | 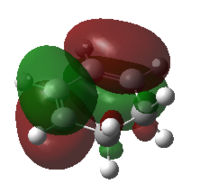 |
 |
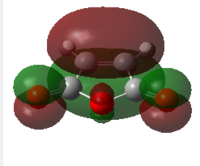 |
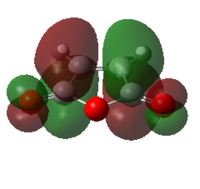
|
| HOMO | LUMO | HOMO | LUMO | |
| Symmetry | antisymmetric | symmetric | symmetric | antisymmetric |
| Energy/Hartree | -0.32074 | 0.01692 | -0.44186 | -0.05949 |
| ENDO | EXO | |||
| MO | 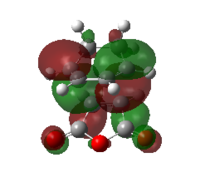 |
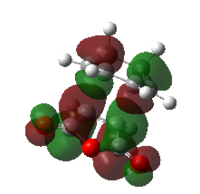 |
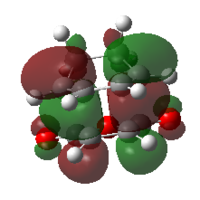 |
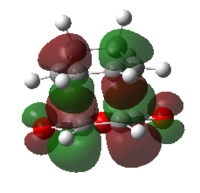
|
| HOMO | LUMO | HOMO | LUMO | |
| Symmetry | antisymmetric | antisymmetric | antisymmetric | antisymmetric |
| Energy/Hartree | -0.34505 | -0.03570 | -0.34275 | -0.04045 |

Using frontier moleculr orbital theory on the reactants and the transition state structure we can deduce the reaction path of the Diels-Alder reaction i.e. which HOMO and LUMO of the reactants took part in the reaction to form the transition state. For the Endo and Exo transition state the HOMO and LUMO are antisymmetric which suggests the HOMO of cyclohexa1,3-diene and the LUMO of the maleic anhydride takes part in this reaction path as they are antisymmetric in symmetry through the reflection plane of symmetry. However as shown by the previous prototypical cycloaddition reaction the LUMO of the transition structure was therefore the opposite symmetry label to the HOMO i.e. symmetric, but this is not that case for this particular Diels-Alder reaction. This can be attributed to the high electronegativity of the oxygen in maleic anyhydride thus oxygen's ability to pull electron away from the double bond in maleic anhydride and the lowering of the energy of the HOMO for maleic anyhydride. Looking at the energy of the bond shown in the table above we can suggest the energy for the HOMO of maleic anhydride is too low in energy (-0.44186) relative to the LUMO of the cyclohex1,3-diene(0.01692) (which is of the same symmetric symmetry) to interact and mix i.e. the HOMO of maleic anhydride is inaccessible, therefore cannot take part directly in the reaction path of the Diels-Alder reaction.
So theoretically the LUMO of cyclohexa1,3-diene and the HOMO of maleic anhydride is an allowed reaction path, it does not occur resulting in the HOMO and LUMO for both Exo and Endo product to be antisymmetric resulting from the mixing of the HOMO of cyclohexa1,3diene and LUMO of maleic anhydride.
Once again an IRC was ran on the same level of theory with both the forwards and back reaction selected to run, force constant set to calculate always and number of points chosen to be assessed as 120. This allows us to probe whether a transition state was found as well as calculating the activation energy and Gibb's free energy to assess the thermodynamic and kinetic properties of the reaction. The actual number of points calculated on the IRC graph for the Endo conformer was 108 and for the Exo conformer was 93.
| IRC of Diels Alder reaction ENDO | Animation of reaction |
| IRC of Diels Alder reaction EXO | Animation of reaction |
The calculated activation energy for the Endo conformer was 26.9kclamol-1 with Exo activation energy being 28.2kcalmol-1. This shows the activation barrier is lower for the Endo confomrer and therefore the rate of this reaction pathway through the Endo transition state is faster than the reaction path way via the Exo conformer i.e. kinetically Endo is faster than Exo. The Gibb's Free energy for the Endo conformer was calculated to be 41.3kcalmol-1 with Exo conformer being 40.5kcalmol-1, as both these reactions are exothermic the Endo conformer's larger more negative Gibbs free energy show a greater stabilisation of the reaction. The lower potential energy of the product formed from the Endo conformer at -100.5kcalmol-1 compared to Exo conformer at -100.3kcalmol-1 also aligns the thermodynamic stability towards Endo conformer.
These values are indicative of the stereospecificity of the Diels-Alder reaction with the Endo product being the major isomer over the Exo product. In a non-ring system for the diene the Exo product is generally the more thermodynamically stable product due to steric hindrance of the substituents on the diene with the dienophile in the Endo transition state which isn't present in the transition state for the Exo transition state. However in our example with cyclohexa-1,3-diene this steric hindrance is not present here resulting in the endo product being the thermodynamically and kinetically favoured product and transition state.
It is also pertinent to mention secondary orbital overlap[12] that occurs during the transition structure for just the Endo conformer where there is stabilisation of the transition structure due to overlap by the π orbitals of the double bond in the dienophile with the HOMO of the diene due to the approach and orientation of the molecules. This secondary orbital overlap is not present in the Exo transition structure as shown by the figure below.
| ENDO-primary and secondary overlap, side profile | EXO-primary over lap, side profile |
The number of nodes within the HOMO of the EXO and ENDO transition structure is 10, this is rather high showing the relative antibonding nature of the molecule however there are large areas of strong bonding orbital interaction especially between the п bonds. of the reactants. What is interesting to notice are the electron densities around the carbonyl and ether fragments in the transition structure, they are very small relative to the large areas of electron density around the rest of the molecule showing their lack of participation in the Diels-Alder reaction but the large electronegativity of the oxygen does play a significant role in the maleic anhydride in lowering the overall energy of the HOMO of the maleic anhydride.
Ab initio calculations would be a better method to use overall for analysis as the calculations uses entirely quantum mechanic techniques to solve the Schrödinger equation without making simplification. The size of the molecule makes no difference to the accuracy of the calculation and therefore makes ab initio method superior to the methods used in this experiment. Sadly these calculations would require super computers and more time in the world, in other cases some calculations could also be stuck in a loop!
Conclusion
The power of computational chemistry is exemplified in the pericyclic reactions discussed here. Having used two very different types of methods from the archaic molecular mechanics towards the higher semi-empirical methods of calculations to delve into the deep dark corners of molecular analysis ranging from simple optimisation and frequency calculations to intrinsic reaction co-ordinate pathways I find myself in awe at a software capable of churning a myriad of data in order to form tangible results in a qualitative and quantitative manner.
From looking at just the HOMO-LUMO of the starting materials and product we can see the allowed pathways of the reaction by using the frontier molecular orbital theory This is an incredible useful, powerful and above all accurate assessment of pericyclic reactions.
The sensitivity of a molecule towards finding it's most stable conformer has been an interesting journey with steric and electronic effects to be taken account of and the most stable conformer is not always the obvious choice. Using different calculation methods also showed how certain calculations are not suitable for certain analysis and computational chemistry really is a compromise between cost and accuracy.
References
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:dont_panic. Last Accessed 07/12/12
- ↑ B. W. Gung, Z. Zhu and R. A. Fouch, J. Am. Chem. Soc, 1995, 117, 17831788
- ↑ B. G. Rocque, J. M. Gonzales and H. F. Schaefer III, Molecular Physics, 2002, 100,4, 441-446DOI:10.1080/00268970110081412
- ↑ http://research.cm.utexas.edu/nbauld/teach/cyclohex.html. Last Accessed 04/12/12
- ↑ 5.0 5.1 5.2 M. D. Harmony; Journal of Chemical Physics, 1990, 93, 7522 DOI:10.1063/1.459380
- ↑ 6.0 6.1 F.H. Allen, O. Kennard, D. G. Watson; J. Chem. Soc. Perkin Trans II, 1987, 2, s1-s19
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3. Last Accessed 04/12/12
- ↑ http://www.ch.ic.ac.uk/local/organic/pericyclic/. Last Accessed 05/12-12
- ↑ 9.0 9.1 A. Bondi, J. Phys. Chem, 1965, 68, 441-451 DOI:10.1021/j100785a001
- ↑ M. J. S. Dewar, S. Olivella and J. J. P. Stewart, J. Am. Chem. Soc, 1986, 108, 5771-5779 DOI:10.1021/ja00279a018
- ↑ E. Goldstein, B. Beno, K. N. Houk, J. Am. Chem. Soc, 1996, 118, 6036-6043 DOI:10.1021/ja9601494
- ↑ M. A. Fox, R. Cardona and N. J. Kiwiet, J. Ord. Chem., 1987, 8, 1469-1474 DOI:10.1021/jo00384a016
Appendix
Cope Reaarangement
LOG FILES OF CONFORMERS OF 1,5-Hexadiene
LOG FILES OF BOAT AND CHAIR TS
Boat, HF, IRC, Boat, HF, IRC, 0K
Chair, HF, part b, Chair, HF, part d, Chair, DFT
Chair, HF, IRC, Chair, DFT, IRC
Diels-Alder
LOG FILES FOR 1,3-BUTADIENE AND ETHYLENE
LOG FILES FOR CYCLHEXA-1,3-DIENE AND MALEIC ANHYDRIDE