The cope rearrangement tutorial

The Cope rearrangement of 1,5-hexadiene is an example of a [3,3]-sigmatropic shift. The reaction goes via transition state and can take either chair or boat form.

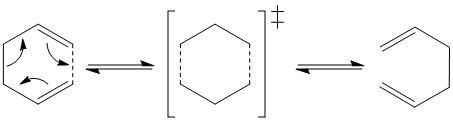
Optimising the reactants and products

In this section the reactants and products which essentially is the same compound - 1,5-hexadiene - is optimised. There are many conformations the molecule could take but there are 10 that are most stable. So the task is to find one with "gauche" and "anti" linkage and their vibrational frequencies and energies are calculated.

(a)

Firstly a structure of 1,5-hexadiene was drawn using the templates in GaussView and the central carbon bond was made antiperiplanar by changing the dihedral angle to 180.

The energy of the molecule=-231.69253527 a.u. and the point group=C_i.

Log file of the calculation:Part (a)

(b)

This time all the C-C and C=C dihedral angles were changed to a gauche conformation meaning that they were ale made 60 degrees.

The energy of the molecule=-231.69153027 a.u. and the point group=C₂.

Log file of the calculation:Part (b)

(c)

This time the C-C and C=C dihedral angles were changed to a +60, -60 and -60 degrees to give the conformation shown on the right. Unfortunately the energy of the molecule is slightly higher than previously not lower as expected.

The energy of the molecule=-231.69166702 a.u. and the point group=C₂.

Log file of the calculation:Part (c)

(d)

Structure	Energy/a.u.	Energy from Appendix 1	Conformer
(a)	-231.69254	-231.69254	anti2
(b)	-231.69153	-231.69153	gauche4
(c)	-231.69167	-231.69167	gauche2

As it can be seen from the table above the energies correspond perfectly to the ones given.

(e)

As it can be seen from part (d) above that my conformer from (a) is anti2 conformer of 1,5-hexadiene. When the energies are rounded down (see table above) it can be seen that they are exactly the same.

(f)

Now the anti2 structure is re-optimised using DFT method with B3LYP/6-31G* basis-set insted of the the HF/3-21G method used before.

The log file of the calculation (f)

The energy of the molecule=-234.61169853a.u. which is approximately 3a.u. higher that the energy of the molecule with the DFT method. However this can be misleading as the energy of the molecule cannot be compared from the use of two different methods and basis sets. It is better to look at the overall geometry of the molecule.

Visually the molecule form the different method calculations look exactly the same. But form the table below we can see that the bonds lengths and bond angles differ slightly. The bond lengths and angles not shown in the table are the same for both the method calculations.

'	C2=C1/Å	C12=C13/Å	C1-C6-C7/°	C6-C7-C12/°	C2-C1-C6-C7/°	C6-C7-C12-C13/°
HF/3-21G	1.32	1.32	111.3	111.3	114.6	114.6
B3LYP/6-31G*	1.33	1.33	112.7	112.7	118.6	118.6

It can be seen that the C=C bonds in the lower accuracy calculation are slightly shorter, this can be considered to be insignificant. The bond angles also only differ by 1.5 - 4 degrees which again is not a significant difference.

All in all it can be considered that both the methods are accurate enough and one does not have strengths over the other one.

(g)

In this part a frequency calculation is carried out on the anti2 conformer with the DFT method and B3LYP/6-31-G* basis-set to confirm that all the vibrations are positive and hence the molecule has it's minimum energy conformation.

The log file for the calculation: (g)

Thermochemistry data fromt the IR calculation:

No.	Energy type	Energy/a.u.
(i)	The sum of electronic and zero-point energies	-234.4692
(ii)	The sum of electronic and thermal energies	-234.4619
(iii)	The sum of electronic and thermal enthalpies	-234.4609
(iv)	The sum of electronic and thermal free energies	-234.5009

Optimizing the "chair" and "boat" transition structures

In this section transition state optimization calculations are performed.

(a)

Firstly an allyl fragment was drawn (CH2CHCH2) and then copied and translated to produce an approximate chair conformation. The two allyl fragments were set 2.2Å apart.

The structure was then optimized using HF/3-21G level of theory.

(b)

Now a transition stae calculation together with a frequency calculation was set up using the same method as before but optimisation was not set to a minimum but to TS(Berny) instead, the force constant was claculated once and the additional keywords were Opt=NoEigen.

The calculation came back with a negative vibration at -818.05cm^-1, which when visualised corresponds to bond making/bond breaking required by the Cope rearrangement. This is shown below:

Chair transition state vibration at -818.05cm^-1

The log file of the calculation: (b)

(c)

Now the transition state is going to be optimised using the frozen coordinate method. The output file from above calculation was taken and the coordinates of the two opposite terminal carbon atoms of the allyl fragments "frozen" (set to 2.2Å). Again the same method and basis-set as above was used.

The log file of the calculation: (c)

(d)

The optimised structure with the frozen method looks much like the optimised structure from part (b) but the bond distances are now 2.2Å - exactly what they were set to be instead of being 2.02Å which is the case in part (b).

The log file of the calculation: (d)

Comparison of parameters of the chair transition state with Method 1 and Method 2:

Parameter	Method 1	'	Method 2	'
	Before	After	Before	After
C-C (terminal)	2.15Å	2.02Å	2.20Å	2.20Å
C-C (allyl)	2.39Å	2.39Å	2.39Å	2.39Å
C3-C1-C6	124.3°	120.5°	122.0°	120.5°
C11-C9-C14	124.3°	120.5°	122.0°	120.5°
Energy/a.u.		-231.6193		-231.6193

From the table above it can be seen that there are some differences between the results of the 2 different methods used for calculations.

Firstly, with method one the C-C (terminal) bond lenght changed when Method 1 was used but not with Method 2 since that was set initially before the calculation. Also it can be seen that the bond angles were higher to start with for Method 1 but in the end for both methods ended to give the same result. However the total energy of the calculation for both the methods is the same, so it can be concluded that both methods are equally good and can be appplied and no significant differences are observed.

(e)

In this part the boat transition state is optimised using the QST2 method and also a frequency calculation is carried out. The atoms were re-labbeled to match each other, but the calculation came back with an error. So then the initial input was taken and the centarl dihedral angle was changed to 0° and the inside C-C-C angles were reduced to 100°.

The log file of the calculation: (e)

(f)

Since it is impossible to predict which to which conformer the transition states will lead to another method can be used. Intrinisic Reaction Coordinate or IRC method which creates a series of small geometry steps. In this calculation the step limit was set to 50.

The log file of the calculation: (f)

From the energy in the log file it can be seen that the structure has not reached it's minimum so there are 3 ways to further minimise the structure.

(i) An optimisation was run on the last point of the IRC. The structure produced was gauche2 with the right energy.

The log file of the calculation: f(i)

(ii) The IRC was computed again with a larger number of steps, so instead of 50 steps 75 were used. This conformation does not seem to correspond to any of the structures that can be compared to.

The log file of the calculation: f(ii)

(iii) The IRC was computed again specifying that the force constant has to be calculated at each step. Again, as in part (i) above, the structure produced was gauche2 with the right energy.

The log file of the calculation: f(iii)

(g)

The activation energies in this step will be calculate using B3LYP/6-31G* level of theory starting with the HF/3-21G optimized structures and frequency calculations are carried out.

The symmetries produced were exactly the same, but the energies differed by about 3 a.u. for both conformations.

Method	Chair structure energy/a.u.	Boat structure energy/a.u.
HF/3-21G	-231.6193	-231.6028
B3LYP/6-31G*	-234.5570	-234.5431

The Diels Alder cycloaddition

The Diels Alder reaction is classified as a pericyclic reaction, where the π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene.

(i)

Cis-butadiene was drawn and optimised using the AM1 semi-empirical molecular orbital method.

The log file for the calculation:(i) The point group for cis-butadiene is C_2v.

Below the HUMO and LUMO molecular orbitals of cis-butadiene are shown:

From the molecular orbital images above it can be seen that HUMO is asymmetric and LUMO is symmetric.

(ii)

Now the transition state geometry will be calculated and the reaction path examined.

The transition state was drawn in GaussView starting with a bicyclo system and then the -CH2-CH2- fragment was removed. The distances between the C-C bonds of the dienophile and diene were set to be 2.2Å and the method used was HF/3-21G with TS(Berny) with additional key words Opt=NoEigen.

The log file for the calculatio:(ii)

An IR calculation was also run to confirm that this is the true transition state. An imaginary vibration at -609.84cm^-1 was produced which corresponds directly to a Diels Alder reaction of a dienophile and diene frorming/breaking bonds.

The log file for the calculatio:(ii) IR

Below is the HOMO of the transition state:

From the image above it can be seen that the HOMO of the transition state is symmetric just like the LUMO of the cic-buradiene from before.

References

V. N. Staroverov and E. R. Davidson., J. Am. Chem. Soc., 2000, 122 (30), 7377–7385. DOI:10.1021/ja001259k
S. Sakai., International J. of Quantum Chem., 2000, 80 (4-5), 1099 - 1106. DOI:<1099::AID-QUA59>3.0.CO;2-C 10.1002/1097-461X(2000)80:4/5<1099::AID-QUA59>3.0.CO;2-C
A. Brown., M. J. S. Dewar and W. Schoeller., J. Am. Chem. Soc., 1970, 92, 5516. DOI:10.1021/ja00721a038