Rep:Mod:skn13
Transition States
Introduction
In this lab, three different reactions were explored by looking at the nature of the reactions computed via Transition state geometry and the potential energy surface (PES) using the software GaussView 5.0. Focused mainly are the Diels-Alder cycloadditions between: Ethene with Butadiene, Cyclohexadiene with 1,3-Dioxole and Xylyene with Sulfur Dioxide. Focused also was the Cheletropic reaction between Xylyene and Sulfur Dioxide, which was then compared with the Diels-Alder cycloaddition reaction with the same reactants. Interestingly, every Diels-Alder cycloaddition (except the first reaction between Ethene with Butadiene since the dienophile, Ethene, is symmetrical with respect to all of its substituents) had two different possible Transition states: Exo and Endo; which was also explored. Firstly in order to progress with the understanding of this study, we must define what the Transition State is and its implications.
It is defined as the state corresponding to the highest potential energy along this reaction coordinate [1]. In fact, it is a theoretical state which can't be isolated so computational analysis is done in order to confirm and/or make clearer its structure. So by just looking at the applications of computational chemistry i.e. determining unknown structures of synthesis reactions, one can see the value it has in chemistry. Computational chemistry utilises the intrinsic properties of atoms, molecules, structures and bonds to compute calculations which otherwise would have been less facile and a waste of time. It is efficient and therefore used in this study for calculating results through available methods present in the software such as Semi-Empirical (PM6) and DFT (B3LYP/6-31G(d) to obtain characterisations such as vibrational frequencies, optimisations to minimum and transition states and intrinsic reaction coordinates (IRC).
Confirmation of reaching the Transitions state structure is relatively facile due to the intrinsic property that is the state itself. The Transition state is a saddle point on a PES, like energy minimas, where the total forces acting is 0. As this is first order with respect to the PES, it is expected that such "energy maxima" would correspond to a negative value when differentiated again because moving in either directions with respect to the maxima would result in a decrease in energy. Likewise, energy minimas would correspond to a positive value as moving away from the minima would result in an increase in energy. Differentiating the force gives the force constant, k, and since the vibrational frequency is proportional to the square root of force constant, square rooting a negative force constant will give an imaginary solution for the vibration frequency. Therefore, the presence of an imaginary frequency confirms the Transition state.
Nf710 (talk) 23:39, 19 January 2017 (UTC) Your description of a TS is wrong.first order TS means all coordinates apart from one have a positive force constant with only on co ordinate having a maximum this is the reaction coordinate.
Reaction between Ethene and Butadiene
Background information


The reaction between ethene and butadiene proceeds as an intermolecular Diels-Alder reaction, a [4+2] cycloaddition reaction where the reaction is between a dienophile (ethene) and a diene (butadiene) and where the numbers correspond to the number of atoms in each component participating in the cycloaddition, 4 carbon atoms from the butadiene and 2 from ethene. The reaction is only possible when the diene is in the unfavoured, due to sterics and electron repulsion, cis conformation as opposed to the trans conformation because of the latter's resultant adduct is too strained. As mentioned in the introduction, since ethene's substituents are all the same (4 Hydrogens), stereospecificity is not considered when concerning the approach of the diene to the dienophile because only one possible product can form, cyclohexene.
To assess first whether a reaction is possible between components, the orbital symmetry must be looked into detail. A reaction is thermally allowed when the components obey the Woodward-Hoffman rules where the sum of the components, (4q + 2)s and (4r)a (both q and a have to be integers and s = suprafacial and a = antarafacial), must be odd. In this particular cycloaddition, because there are 4pi electrons from the diene and 2pi electrons from the dienophile q is therefore equal to 1 and r is 0, thus giving a total of 1, an odd number, so the reaction is thermally allowed.
The interaction between the HOMO of the diene and the LUMO of the dienophile is favoured over the reverse because these molecular orbitals are closer in energy and therefore the orbital overlap is better resulting in a greater overall stabilisation of the molecule. This is clearly displayed in Fig 2, where this interaction results in a larger splitting therefore the 1Pig (1πg) MO is lower in energy than that of the 2Piu (2πu) MO.
Molecular Orbitals in play
 |
 |
 |
 |
 |
 |
 |
 |


For a symmetric-symmetric interaction about the plane of symmetry (see Fig 11), the HOMO of the ethene (Fig 6) and LUMO of butadiene (Fig 3), it is clear by looking at the orbitals that the overlap integral will be non-zero. For a symmetric-asymmetric interaction, the HOMO of ethene (Fig 6) with HOMO of butadiene (Fig 4), the reaction over lap integral will be zero because there are equal bonding and anti-bonding overlap, thus resulting in an overall zero overlap. However for an asymmetric-asymmetric interaction, the HOMO of butadiene (Fig 4) and LUMO of ethene (Fig 5), despite the orbitals being asymmetric about the plane of symmetry, the orbitals can overlap because they are of the correct symmetry with respect to overlap. Hence, the overlap integral is non-zero.
As shown above, these MO's in the reactants are all participating in forming new molecular orbitals in the transition with the combination that matches it's symmetry, of course the correct orientation too is imperative. Therefore with enough overlap, as long as the HOMO of one reactant is equipped with the correct symmetry to interact with the LUMO of the other reactant, then this reaction can proceed. In standard natural polarity Diels-Alder reaction, the HOMO from the diene interacts with the LUMO of the dienophile but the reverse may happen too where the HOMO from the dienophile and the LUMO from the HOMO interact in an inverse demand Diels-Alder reaction. Either way, the reaction can proceed with the requirement that the HOMO-LUMO combination is of the correct symmetry. The reaction is forbidden in the case of incorrect symmetry resulting in no interaction from the HOMO from one reactant and the LUMO of the other.
Nf710 (talk) 23:55, 19 January 2017 (UTC) Goos understanding of inverse reactions etc. YOu have suggest what this reaction could be.
Bond Lengths
During the course of the reaction, it is quite clear that the length of the ethene carbon=carbon double bond lengthens and this is what is expected. During the Transition state, there is bond lengthening for all double bonds because the electron density is being donated in the to pi* anti-bonding orbital and weakening the bond. What is also expected is the single carbon-carbon bond to shorten, as this is where the double bond forms in the product. Since the transition state is intermediate between the starting material and products (neither a bond order of 1 or 2 but in between) its bond length too is also intermediate in value and this is further reflected and confirmed by the extreme values of bond lengths in the product, cyclohexadiene. The carbon=carbon double bonds, in the original butadiene and ethene, have overall lengthened (C1-C2, C13-12, C8-C7) and the single bond from the butadiene (C12-8) has shortened, reflecting the formation of a pi bond. Furthermore, we can see the formation of the bond between the ends of butadiene and ethene (C2-13 and C7-C1) because the distance at the transition state is too far apart meaning the bond hadn't quite formed as of yet but in the product, the sigma bond has formed. An sp3 carbon length is typically 1.54 Angstroms and an Sp2 carbon length is 1.34 Angstroms[2] so the transitional state matches with being intermediate between the literature values. According to the literature, the van der waals radium for a carbon atom is 1.70 angstroms[3]. This radius is a lot lower than that of the partly formed carbon-carbon bond (cf. 2.11 angstroms) in the transition state (C2-13 and C7-C1) showing that these bonds in the transition state have not come close enough to full form a bond with the order of 1.
| Type | Bonds | Length (Angstroms) | Literature[2] |
|---|---|---|---|
| Reactants | Butadiene C-C | 1.47 | 1.474 |
| Butadiene C=C | 1.34 | 1.350 | |
| Ethene C=C | 1.33 | ||
| Transition state[4] | C1-C2 | 1.38 | 1.39 |
| C2-C13 | 2.11 | 2.27 | |
| C13-C12 | 1.38 | 1.38 | |
| C12-C8 | 1.41 | 1.41 | |
| C8-C7 | 1.38 | 1.38 | |
| C7-C1 | 2.11 | 2.27 | |
| Cyclohexadiene | C1-C2 | 1.53 | |
| C2-C13 | 1.54 | ||
| C13-C12 | 1.50 | ||
| C12-C8 | 1.34 | ||
| C8-C7 | 1.50 | ||
| C7-C1 | 1.54 |
Reaction path at Transition state
Now the question is, how does the reaction proceed? Well, Diels-Alder reactions are particularly useful in organic synthesis because it is an effective pericylic reaction that is stereospecific. Meaning stereochemistry in the reactants is retained in the adduct. How? One needs only to look at the vibrations.
As you can see, the vibrations above shows that the reaction is synchrous.
Reaction between 1,3-Dioxole and Cyclohexadiene

Like the previous reaction, the one between 1,3-dioxole and cyclohexadiene is a [4+2] cycloaddition Diels-Alder reaction. Unlike the previous reaction however, because the dienophile, 1,3-dioxole, has different substituents attached to the double bond, the resultant adduct can be of two forms: exo or endo. Therefore stereospecificity is concerned here and the more favourite product, if there is one, will be further explored. It is well known that though the exo adduct's structure is less hindered than that of the endo but it also misses out on the favourable orbital interaction that is only possible in the endo conformation. How do we know this? One needs only to look at the transition states to see why. One thing to note for Diels-Alder reaction is the natural polarity for it's reactants. Usually, under natural polarity, for the interaction of orbitals to form the product, the LUMO of the dienophile interacts with the HOMO of the diene. For an unnatural polarity or inverse demand Diels-Alder reaction, the LUMO of the diene interacts with the HOMO of the dienophile instead. So LUMO lowering and HOMO raising substituents are preferred to heighten the facileness of a reaction and thus facilitate the formation of two new sigma bonds. So a good indication before inspecting orbitals whether a reaction is of the normal or inverse demand, are the substituents on the dienophile and diene respectively.
Molecular Orbitals in play
With the help of the visualised MO's, it is quite facile to spot which orbitals are in play in which transition state. It doesn't matter which MO, HOMO or LUMO, of the transition state under inspection but to stay consistent only the HOMO's of both Exo and Endo transitions states will be observed in detail to identify which polarity of Diels-Alder reaction it undertakes. The HOMO of the Endo transition state (Fig 18), focusing just on the dienophile fragment, above and below the oxygens (red atoms), we can spot a MO of pi bonding symmetry and this is the same for the Exo transition state too. Because the HOMO is lower in energy than the LUMO, it can be deduced therefore which MO from the dienophile contributes to the bonding molecular orbital, either HOMO or LUMO. When comparing Fig 15 with Fig 17 it is clear that the contributing MO from the dienophile is the HOMO of the 1,3-dioxole. Hence, this follows unnatural polarity and hence both the Exo and Endo Diels-Alder reactions are of the inverse demand.
| Exo energies (kJ/mol) | Endo (kJ/mol) | |
|---|---|---|
| Reactants | -313996.61817 | -313996.61817 |
| Transition state | -313956.55041 | -313958.42350 |
| Products | -314011.86014 | -314012.73049 |
| Ea | 40.06776 | 38.19467 |
| Gibbs Free Energy | -55.30973 | -54.30699 |
The output of energies were really similar for both the endo and exo pathways. Both were similar in terms of the product formed being more negative in energy suggesting that these reactions are exothermic. Though the difference in activation energies is small, the calculated output suggests that the endo pathway proceeds more facile than the exo because the activation energy is smaller. We can justify this by comparing the structures of the transition states. It is possible the clear secondary orbital interaction present in the endo transition state (Fig 18) that is absent in the exo transition state (Fig 20). This favourable secondary orbital interaction, though small, stabilises the transition state and therefore lowers the energy of the transition state, making the reaction easier to proceed. Furthermore, we can conclude that the endo product is smaller than than of the exo so not only is the endo pathway kinetically more stable, it is also more thermally stable.
Nf710 (talk) 00:14, 20 January 2017 (UTC) Good understanding of the mechanism of an inverse demand reaction.your energies are slightly out but you have still come to the correct concluson you may have used the incrorrect basis perhaps
Reaction between Xylyene and Sulfur Dioxide: Diels Alder vs Cheletropic


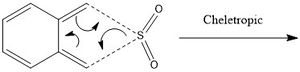
In comparison with the previous two reactions, the study of xylyene reacting with sulfur dioxide gets slightly more complicated because there are not only just 2 possible Diels-Alder reactions but another one via a different mechanism, cheletropic. As with the previous reaction, there are 2 different transition states which lead on to the exo and endo products which energies will be further explored. However due to the possibility of another mechanism via the cheletropic pathway, all these energies will be compared in order to deduce which mechanism the reaction is most likely to undertake. All of these reactions are concerted but they all have different transition states and so it is expected that the endo pathway is more preferred than the exo because of the secondary orbital interactions, identical to the interactions mentioned in the previous reaction.

(For reaction profiles, draw straight lines between stationary points (especially if the lines are fictitious). Tam10 (talk) 15:35, 3 January 2017 (UTC))
| Exo energies (kJ/mol) | Endo (kJ/mol) | Cheletropic (kJ/mol) | |
|---|---|---|---|
| Reactants | 42.4685725 | 42.648665 | 44.56003 |
| Transition state | 57.778945 | 56.825145 | 62.16266 |
| Products | 13.4630125 | 13.6173775 | -0.001255 |
| Ea | 15.3103725 | 14.17648 | 17.60263 |
| Gibbs Free Energy | -44.3159325 | -43.2077675 | -62.163915 |
(It looks like these energies are in kcal/mol Tam10 (talk) 15:35, 3 January 2017 (UTC))
By looking at Fig 35 and the table of the calculated output above, it is clear that the cheletropic pathway results in the most thermodynamic product because it is lowest in energy (and has the most negative gibbs free energy) despite requiring slightly more energy to overcome the activation energy.
During the course of each reaction, the 6-membered ring in xylylene needs on 2 more pi electrons in order to achieve aromatically, a much more stable energy ground state than having a pair of reactive pi bonds. It can be seen that in each of the IRC's of the different pathways and in the transition states above that the ring simultaneously delocalises it's 6 pi electrons to achieve that energy favored state.
With more time in this study, it would be more interesting to compute the rates of reactions for all reactions to confirm which pathways gave the kinetically favored products. Furthermore, it was interesting to see contradicting experimental evidence to the theory where the exo transition state pathway led to a more stable product that the endo. With additional time, this would be further explored. As for the most part, the experimental procedure agreed with the literature for bond lengths so the transition states explored in this study is quite precise.
(Rates would be very crudely approximated using stationary QM calculations. There are other very important factors that are covered in reaction dynamics. If your bond lengths agree with literature, it would be good to see a table where you compare them Tam10 (talk) 15:35, 3 January 2017 (UTC))
== References ==
4. [4] K. Black, P. Liu, L. Xu, C. Doubleday, K. N. Houk, Dynamics, transition states, and timing of bond formation in Diels–Alder reactions, 1, 109, No. 32
- ↑ [1] ^ Transition State, https://en.wikipedia.org/wiki/Transition_state, (15th December 2016)
- ↑ [2] Butadiene: A molecular study, http://chemistry.umeche.maine.edu/Modeling/donmolmech.html, (23rd December 2016)
- ↑ [3] S. S. Batsanov, Van der Waals Radii of Elements, 2001, 879, 37, No.9