Rep:Mod:sk-inorg

Day 1 tasks

BH₃

Optimisation & frequency analysis

BH3 was optimised using the B3LYP method and the 6-31G(d,p) basis set. Below is:

• The summary window, which shows the correct molecular symmetry (D_3h);
• The item table in the log file obtained after the optimisation, which shows that the optimisation is fully completed;
• The low frequencies obtained from the BH3 frequency log file.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000064     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES
 Predicted change in Energy=-1.128858D-09
 Optimization completed.
    -- Stationary point found.

Low frequencies ---  -12.3492  -12.3425   -7.6649   -0.0008    0.0239    0.4061

Low frequencies --- 1162.9695 1213.1356 1213.1358

Optimised BH3 molecule

Vibrational modes

Wavenumber (cm-1)	Intensity (arbitrary units)	Symmetry	IR active?	Vibrational mode
1163	93	A2''	Yes	Out-of-plane bend
1213	14	E'	Very slightly	Symmetric bend
1213	14	E'	Very slightly	Symmetric bend
2583	0	A1'	No	Symmetric stretch
2716	126	E'	Yes	Asymmetric stretch
2716	126	E'	Yes	Asymmetric stretch

Only three peaks are visible in the IR spectrum (instead of the 6 present in the table given above). The vibration at 2583 cm-1 is not present because this frequency is for the symmetric stretch vibrational mode, which doesn't change the dipole moment of the molecule whereas the other vibrations do. A change in dipole moment is needed for a vibration to be IR active as one of the selection rules for this spectroscopy is Δμ ≠ 0, where Δμ is the change in dipole moment. There is also 2-fold degeneracy present for the vibration at the wavenumbers of 1213 and 2716 cm-1, removing two possible peaks and this means only one peak will be present at these frequencies.

Molecular orbital diagram

Molecular orbital diagram of BH3, with the computed MOs (calculated using the Gaussian software) shown alongside the LCAO MOs

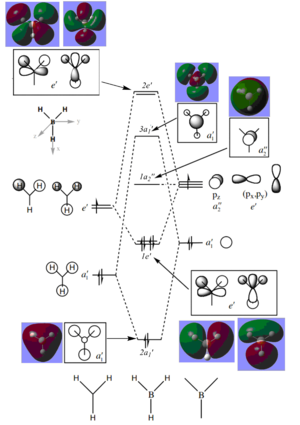
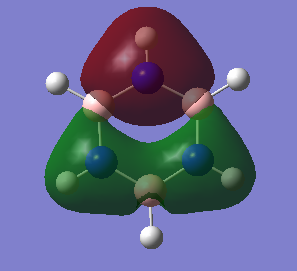
The molecular orbital diagram of BH3 is given with the computed molecular orbitals alongside the predicted LCAOs molecular orbitals.

The 1s orbital of boron (of 1a₁' symmetry) was ignored in the diagram as it is too deep in energy to combine with any other hydrogen orbitals. Due to hydrogen being more electronegative than boron:

• The highest energy orbitals of boron, the 2p orbitals, are placed higher up in the diagram than the halfway point of the H₃ fragment orbitals
• The bonding orbitals have a larger contribution from the H3 FOs and a smaller contribution from the boron AOs (and vice versa for the antibonding orbitals)

In general, the computed MOs agreed with the predicted ones as the shapes where very similar, showing that qualitative MO theory is useful as it uses relatively simple principles to predict the shapes of the actual MOs, with quite good accuracy; however, there is one significant slight discrepancy: there was a greater contribution from the 1s hydrogen orbitals in the antibonding MOs, especially in the 3a₁' MO, where it was predicted that the boron 2s orbital would have a greater contribution due to boron being more electronegative than hydrogen. This shows that qualitative MO theory is not completely accurate as this difference suggests that merely using the electronegativities of boron and hydrogen to create the MOs won't always lead to the correct shapes.

Ng611 (talk) 13:15, 5 June 2018 (BST) Excellent!

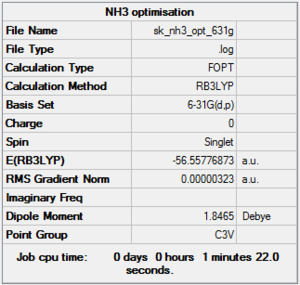
NH₃

NH3 was optimised using the B3LYP method and the 6-31G(d,p) basis set. Below is:

• The summary window, which shows the correct molecular symmetry (C_3v);
• The item table in the log file obtained after the optimisation, which shows that the optimisation is fully completed;
• The low frequencies obtained from the NH3 frequency log file.

Optimisation & Frequency analysis

         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000012     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES
 Predicted change in Energy=-9.843984D-11
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---   -0.0138   -0.0032   -0.0015    7.0783    8.0932    8.0937
 Low frequencies --- 1089.3840 1693.9368 1693.9368

Optimised NH3 molecule

NH₃BH₃

NH₃BH₃ was optimised using the B3LYP method and the 6-31G(d,p) basis set. Below is:

• The summary window, which shows the correct molecular symmetry (C_3v);
• The item table in the log file obtained after the optimisation, which shows that the optimisation is fully completed;
• The low frequencies obtained from the NH₃BH₃ frequency log file.

Optimisation & Frequency analysis

         Item               Value     Threshold  Converged?
 Maximum Force            0.000122     0.000450     YES
 RMS     Force            0.000058     0.000300     YES
 Maximum Displacement     0.000531     0.001800     YES
 RMS     Displacement     0.000296     0.001200     YES
 Predicted change in Energy=-1.655851D-07
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---   -0.0251   -0.0033   -0.0008   17.1236   17.1258   37.1326
 Low frequencies ---  265.7816  632.2034  639.3483

Optimised NH3BH3 molecule

Association energy of NH₃BH₃

E(NH₃) = -56.55777 a.u.

E(BH₃) = -26.61532 a.u.

E(NH₃BH₃) = -83.22468 a.u.

ΔE = E(NH₃BH₃)-[E(NH₃)+E(BH₃)] = -0.05159 a.u. = -135 kJ/mol

Compared to an isolectronic molecule of ethane, with a bond energy of around 376.2 kJ/mol, this value seems quite weak, despite it having a negative change, meaning that this adduct formation is still an exothermic reaction.

BBr₃

NH3 was optimised using the RB3LYP method and the GEN basis set. Below is:

• The summary window, which shows the correct molecular symmetry (D_3h);
• The item table in the log file obtained after the optimisation (DOI:10042/202460 ), which shows that the optimisation is fully completed;
• The low frequencies obtained from the BBr3 frequency file: DOI:10042/202461

Ng611 (talk) 13:16, 5 June 2018 (BST) You mean LANL2DZ/6-31G -- Gen is not a valid basis set descriptor.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000024     0.001200     YES
 Predicted change in Energy=-4.085774D-10
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---   -2.3055   -0.0029   -0.0018    0.0774    0.7534    0.7534
 Low frequencies ---  155.9402  155.9405  267.6894

Optimised BBr3 molecule

Aromaticity project

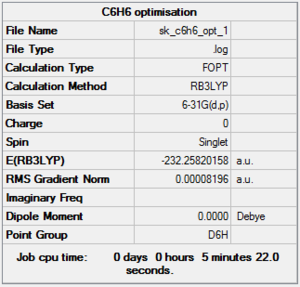
Benzene

Benzene was optimised using the B3LYP method and the 6-31G(d,p) basis set. Below is:

• The summary window, which shows the correct molecular symmetry (D_6h);
• The item table in the log file obtained after the optimisation, which shows that the optimisation is fully completed;
• The low frequencies obtained from the C₆H₆ frequency log file.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000193     0.000450     YES
 RMS     Force            0.000079     0.000300     YES
 Maximum Displacement     0.000830     0.001800     YES
 RMS     Displacement     0.000294     0.001200     YES
 Predicted change in Energy=-4.437902D-07
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---  -17.2053  -14.9372  -14.9372   -0.0055   -0.0055   -0.0007
 Low frequencies ---  414.1053  414.1053  620.9426

Optimised benzene molecule

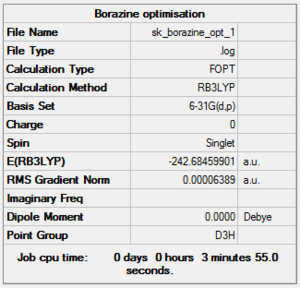
Borazine

Borazine was optimised using the B3LYP method and the 6-31G(d,p) basis set. Below is:

• The summary window, which shows the correct molecular symmetry (D_3h);
• The item table in the log file obtained after the optimisation, which shows that the optimisation is fully completed;
• The low frequencies obtained from the Borazine frequency log file.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000085     0.000450     YES
 RMS     Force            0.000033     0.000300     YES
 Maximum Displacement     0.000250     0.001800     YES
 RMS     Displacement     0.000075     0.001200     YES
 Predicted change in Energy=-9.233282D-08
 Optimization completed.
    -- Stationary point found.

 Low frequencies ---   -0.0105   -0.0090   -0.0035    2.8223    2.8805    4.1465
 Low frequencies ---  289.7095  289.7101  404.4118

Optimised borazine molecule

NBO charge analysis

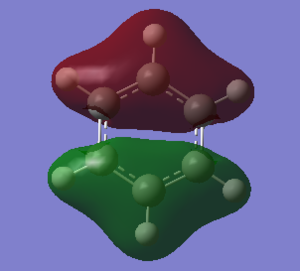
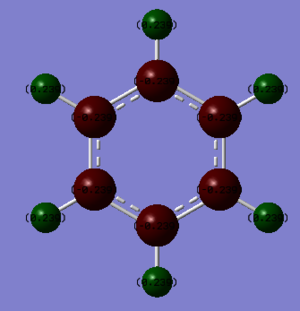
The table below shows the results from the NBO charge analysis of benzene and borazine. In the images below, a colour scale of -1.10 (red) to +1.10 (green) was used and black corresponded to a charge of 0. The charges of each atom in the molecule given below the corresponding image.

Benzene	Borazine
C = -0.24	N = -1.10
H = 0.24	H in NH unit = 0.43
	B = 0.75
	H in BH unit = -0.08

Being symmetric, both molecules have no dipole moment (all of the charges in each molecule add up to 0), although the charge distribution has symmetry corresponding to the point group of the molecule: all of the symmetry operations in benzene's point group (D_6h) can be performed on the charge distribution and it will map onto itself and the same is true for borazine's charge distribution using the symmetry operations in the D_3h point group. The C-H bonds in benzene are only very slightly polarised, with the carbon atoms being red as it's slightly more electronegative than hydrogen. Borazine's charge distribution is more varied because of the alternating nitrogen/boron pattern in the ring. The nitrogen atoms are bright red because they are the most electronegative atoms present and the boron atoms are bright green as, even though they have a similar electronegativity to the hydrogen atoms, each boron is between two nitrogen atoms, so it will have a more positive charge compared to the hydrogen atoms. The Hydrogen atoms in the NH units have a greater positive charge than the H atoms in the BH units due to being bonded to a more electronegative atom (nitrogen), so more electron density is removed from H than when bonded to B.

Ng611 (talk) 13:21, 5 June 2018 (BST) A thorough but efficient discussion -- well done. Another interesting point to note is that the total partial charge value of each B-H/N-H pair is identical.

Comparison of benzene and borazine MOs

In the following discussion, the z-axis is taken to be the principal axis of each molecule.

Benzene	Borazine	Comparison
		This is MO 17 of both molecules, which corresponds to the 2pz orbitals of carbon combining in-phase in benzene and the 2pz orbitals of boron and nitrogen combining in-phase in borazine. This MO for both molecules are very similar because they're symmetric, although the MO for borazine has a C3 axis (and not the C6 present in benzene) due to the greater contribution from nitrogen due to its greater electronegativity. There is a nodal plane between the lobes - along the σh plane.
		This is MO 9 for both molecules. In benzene, this has bonding character between the 3 carbon 2s and the 3 hydrogen 1s orbitals in each half of the molecule and antibonding character between the two halves of the molecule. In borazine, only the NH units contribute to this MO, with one NH unit (N's 2s and H's 1s AOs) in a different phase to the 2 other NH units. Benzene's MO is has a C2 rotational axis borazine's doesn't
		This is the MO 20 (the HOMO) for both molecules, which is the in-phase combination of 2 pairs of 2 adjacent 2pz orbitals. In both molecules, there is no contribution from the two atoms on opposite sides of the ring. It is evident that the MO in borazine is distorted towards the nitrogen atoms, which is caused by the nitrogen atoms having a bigger contribution due to its higher electronegativity than the boron atoms.

Ng611 (talk) 13:26, 5 June 2018 (BST) Good comparisons made here. Some other points to consider would be the character (sigma, pi, etc.) of the orbital and also their symmetry labels.

Aromaticity

Aromaticity can be explained simply using Hückel's rules, where an aromatic molecule fulfils these rules:

• It must be planar,
• Cyclic,
• Have a contiguous array of p orbitals orthogonal to the plane of the ring
• Have 4n+2 electrons in these p orbitals, where n is an integer

Benzene and borazine both comply with these rules as they're both cyclic and planar, each with 6 electrons in the p_z orbitals (each carbon contributes 1 electron in benzene; in borazine, each B contributes no electrons and each N has 2 electrons in the p_z orbitals) and MO 17 for both shows the contiguous array of p_z orbitals.

It is known that there is a "resonance energy" associated with aromatic compounds, which makes them very stable compounds. In an applied magnetic field, the ring current in aromatic systems creates its own induced magnetic field. The effect of this is that outside the ring, the induced field is in the same direction and the applied field, so hydrogens outside the ring would be deshielded in an NMR spectrometer. The opposite is true inside the ring.

It has been suggested that the sigma framework in aromatic molecules (the p orbitals combining in-phase in the plane of the ring) is an important bonding mode as well, not solely the p_z orbitals.

Ng611 (talk) 13:27, 5 June 2018 (BST) I would suggest adding more detail/exposition in this section, although the points that you've made are all correct and accurate.

Ng611 (talk) 13:28, 5 June 2018 (BST) An excellent report overall, well done. Besides some missing detail in one or two discussions, there is very little to criticize here. Very well done.