Rep:Mod:shine11

Inorganic Computational Chemistry

Optimisation

BH₃

3-21G

The log file for the optimisation is Media:JS_BH3_OPT3.LOG

All bond distances are reported to two decimal places, bond angles are reported to one and the dipole moment is reported to two. This is a result of the fact that the program is only accurate to this level of precision.

The optimised B-H bond distance is 1.20A^o and the optimum bond angle is 120.0^o.

	BH₃
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	3-21G
Final energy/au	-26.4622
Gradient/au	0.00004507
Dipole moment/D	0.00
Point group	D_3h
Time taken/s	7.0

          Item               Value     Threshold  Converged?
 Maximum Force            0.000090     0.000450     YES
 RMS     Force            0.000059     0.000300     YES
 Maximum Displacement     0.000352     0.001800     YES
 RMS     Displacement     0.000230     0.001200     YES
 Predicted change in Energy=-4.580958D-08
 Optimization completed.
    -- Stationary point found.

6-31G(d,p)

The log file for this, more accurate optimisation, is Media:JS_BH3_OPTACCURATE.LOG.

The optimised average bond length is 1.20A^o and the optimised bond angle is 120.0^o.

	BH₃
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31g(d,p)
Final energy/au	-26.6153
Gradient/au	0.00000673
Dipole moment/D	0.00
Point group	Cs
Time taken/s	13.0

         Item               Value     Threshold  Converged?
 Maximum Force            0.000011     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000056     0.001800     YES
 RMS     Displacement     0.000036     0.001200     YES
 Predicted change in Energy=-9.815639D-10
 Optimization completed.
    -- Stationary point found.

GaBr₃

GaBr₃ Optimisation D-space

The optimised bond length is 2.35A^o and the optimised bond angle is 120.0^o. This compares reasonably well to a literature vale of 2.38A^o^[1].

	GaBr₃
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	LANL2DZ
Final energy/au	-41.7008
Gradient/au	0.00000016
Dipole moment/D	0.00
Point group	D_3h
Time taken/s	52.1

     Item               Value     Threshold  Converged?
Maximum Force         0.000000    0.000450    YES
RMS Force             0.000000    0.000300    YES
Maximum Displacement  0.000003    0.001800    YES
RMS Displacement      0.000002    0.001200    YES
Predicted change in Energy=-1.282692D-12
 Optimization completed.
    -- Stationary point found.

BBr₃

BBr₃ D-space

The optimised bond length is 1.93A^o and the optimised bond angle is 120.0^o.

	BBr₃
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-64.43644
Gradient/au	0.00001054
Dipole moment/D	0.00
Point group	Cs
Time taken/s	20.7

          Item               Value     Threshold  Converged?
Maximum  Force             0.000024   0.000450    YES
RMS      Force             0.000011   0.000300    YES
Maximum  Displacement      0.000167   0.001800    YES
RMS      Displacement      0.000082   0.001200    YES
Predicted change in Energy=-2.420020D-09
 Optimization completed.
    -- Stationary point found.

Bond Length Comparison

	Bond Length/A^o
BH₃	1.19
BBr₃	1.93
GaBr₃	2.35

Changing the ligand from H to Br significantly increases the bond length. The reasons for this are numerous. Firstly, Br has 3 more full s and p orbitals and 1 more full d orbital than H. It is also has three lone pairs, one of which can donate into the empty B p orbital, since the B is sp² hybridised. This actually shortens the bond length. The other lone pair in the p orbital can cause repulsion which lengthens the bond. Changing the central atom from B to Ga also increases the bond length. First, Ga has two extra s and p orbitals, and a full d orbital, which will repel the orbitals on Br. Second, the fact that Ga is less electronegative than B will lengthen the bond, since the Ga will attract the electrons in the bond less strongly.

Defining a chemical bond is not as trivial as the conventional use of a straight line to indicate covalent bond would make it appear. Typically, it is a potential energy minimum of a system, existing as a result of an attractive electrostatic interaction over a distance that is generally between 1.4-3A^o. The strength of these interaction can vary greatly, from the covalent bonding in N₂, to the hydrogen bonds in water. However, many of these interactions exist in molecules, and simply using distance to determine the existence or non-existence of a bond, as Gaussian does, can lead to important interactions not being detected. In molecular orbital theory, any stabilised orbital is considered to be a bonding orbital. Clearly, this is a more accurate method for the determination of bond formation than just using distance, although every single interaction cannot, of course be considered to be a bond. A combination of both methods must be used.

Frequency Analysis

BH₃

This log file for this process is Media:JS_BH3_FREQ3.LOG‎.

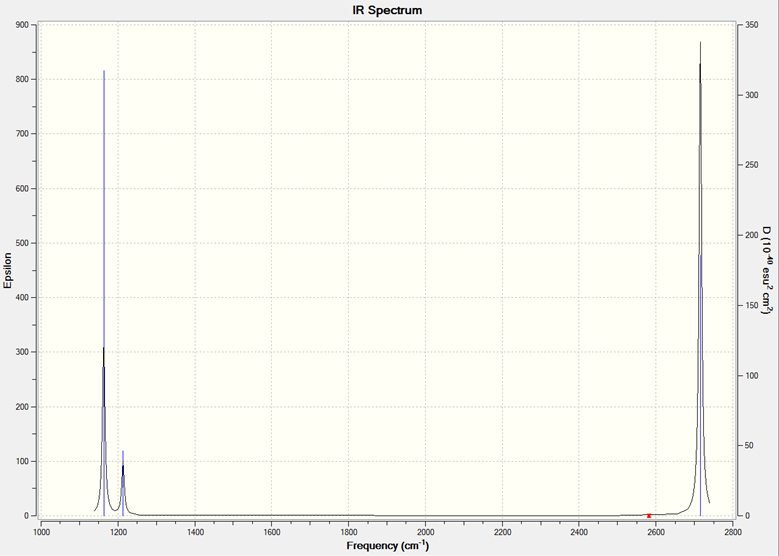
Low frequencies --- -0.9580 -0.9214 -0.0053 5.3695 11.5406 11.5803
Low frequencies --- 1162.9950 1213.1817 1213.1844

	BH₃
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	3-21G
Final energy/au	-26.4622
Gradient/au	0.00008904
Dipole moment/D	0.00
Point group	Cs
Time taken/s	26.0

    Item             Value       Threshold Converged?
Maximum Force        0.000221    0.000450  YES
RMS     Force        0.000106    0.000300  YES
Maximum Displacement 0.000724    0.001800  YES
RMS Displacement     0.000445    0.001200  YES 
Predicted change in Energy=-1.667569D-07
Optimization completed.
-- Stationary point found.

Vibration Visualisation

The optimised average bond length is 1.20A^o and the optimised bond angle is 120.0^o. Force constant related to freq. Gaussian bases bonds on distance

Number	Vibration Form	Frequency	Intensity	Symmetry D_3h
1	The H move left and right in a concerted manner, as the B moves in the opposite direction. (bend)	1160	93	A₂
2	The top two H move diagonally in the shown direction, at the same time, while the remaining B and H move slightly up and down. (bend)	1210	14	E'
3	The bottom H moves clockwise as the top two move anticlockwise. The B remains almost totally stationary. (bend)	1210	14	E'
4	The H move out in these directions in a concerted way. The B does not move. (stretch)	2580	0	A₁'
5	The top left H moves away from the B as the top right H is moving towards it. The B and the H remain almost completely still. (stretch)	2720	126	E'
6	The top two H move away from the B, as the other H moves towards it. The B remains almost totally motionless. (stretch)	2720	126	E'

The actual IR spectrum is shown below.

GaBr₃

GaBr₃ Frequency D-Space

-2.3539 -2.3538 -1.3645 -0.0026 0.0044 0.0276

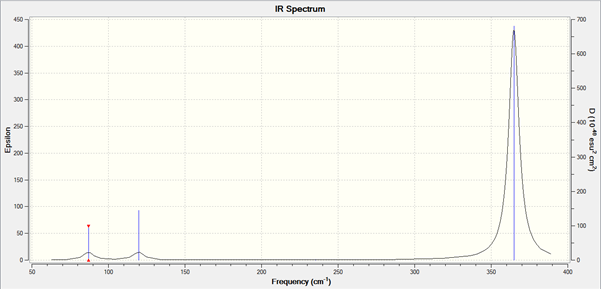
The lowest "real" normal mode is 86.9748cm^-1.

The IR spectrum is below.

Vibration Comparison

Number	Vibration Form	Frequency BH₃ cm^-1	Intensity BH₃	Frequency GaBr₃ cm^-1	Intensity GaBr₃	Symmetry D_3h
1	The H move left and right in a concerted manner, as the B moves in the opposite direction. (bend)	1160	93	120	4	A₂
2	The top two H move diagonally in the shown direction, at the same time, while the remaining B and H move slightly up and down. (bend)	1210	14	87	2	E'
3	The bottom H moves clockwise as the top two move anticlockwise. The B remains almost totally stationary. (bend)	1210	14	87	2	E'
4	The H move out in these directions in a concerted way. The B does not move. (stretch)	2580	0	235	0	A₁'
5	The top left H moves away from the B as the top right H is moving towards it. The B and the H remain almost completely still. (stretch)	2720	126	365	62	E'
6	The top two H move away from the B, as the other H moves towards it. The B remains almost totally motionless. (stretch)	2720	126	365	62	E'

The frequencies of BH₃ are much greater than for GaBr₃, for the same vibrational mode. The main reasons for this are that, first, the frequency is inversely proportional to the reduced mass. Since the reduced mass of GaBr₃ is obviously much greater, its frequencies are reduced. Second, frequency is proportional to the force constant of the bond. The Ga-Br bond is longer than the B-H bond, suggesting that it is a weaker bond. Therefore, its frequencies are again reduced.

Interestingly, bends 2 and 3 are at higher frequency than bend 1 for BH₃, but are at lower frequency than bend 1 for GaBr₃. Apart from this, the spectra a reasonably similar, apart from the fact that the GaBr₃ A₂ bend has a lower intensity. Bends 1,2 and 3 are at similar frequencies, since they are bends. Stretches 4,5 and 6 are also at similar frequencies, because they are stretches. The intensity of stretch 4 is zero, since this stretch causes no change in dipole moment of the molecule. There are only three peaks seen due to the degeneracy of the E' vibrations.

This frequency analysis gives eigenvalues that represent the second derivatives of the energy diagram. Therefore, if they are positive, the energy is a minimum. The low frequencies are to do with the idea that each molecule has 3N-6 degrees of freedom, specifically the "-6", meaning the motions of the center of mass of the molecule. Clearly, the same method and basis set must be used for both pieces of analysis, in order for the results to be compared fairly.

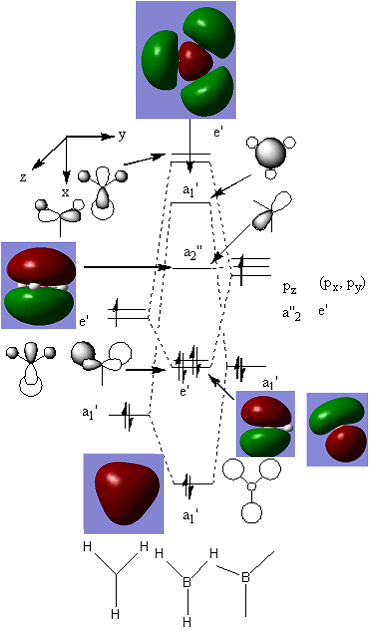
BH₃ MO Analysis

The line "int=ultrafine scf=conver=9" was used to improve the values for the low frequencies.

The log file for the optimisation is Media:JS_BH3_OPT.LOG

   Item                  Value     Threshold  Converged?
 Maximum Force            0.000003     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000013     0.000060     YES
 RMS     Displacement     0.000008     0.000040     YES
 Predicted change in Energy=-6.228076D-11
 Optimization completed.
    -- Stationary point found

The log file for the frequency is Media:JS BH3 FREQ2.LOG.

-11.2361  -11.2272   -5.6980    0.0003    0.0322    0.4463

The D-space for the population analysis is here.

This is the MO diagram with all modeled occupied orbitals and the modeled LUMO.

Comparing the generated orbitals to what MO theory predicted, most of the orbitals appear to be reasonable models of the actual MO, considering the speed of the method. However, the first e' orbital is difficult to view with this program. Also, the rest of the orbitals lack the symmetry that is expected. From this, it also seems that MO theory is useful, for qualitative predictions.

NH₃ NBO Analysis

The log file for the optimisation is Media:JS NH3 OPT.LOG.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000012     0.000300     YES
 Maximum Displacement     0.000079     0.001800     YES
 RMS     Displacement     0.000053     0.001200     YES
 Predicted change in Energy=-1.629715D-09
 Optimization completed.
    -- Stationary point found.

The log file for the frequency is Media:JS NH3 FREQ2.LOG.

-9.3920   -8.3783   -6.3678   -0.0017   -0.0017   -0.0009

This is the D-space for the population analysis.

This is the charge distribution.

The charge range was -1.125 to 1.125

Atom	NBO charge
N	-1.125
H	+0.375

NH₃BH₃ Energy Minimum

The log file for the optimisation is Media:JS NH3BH3 OPT3.LOG.

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000026     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-2.956782D-10
 Optimization completed.
    -- Stationary point found.

The log file for the frequency is Media:JS NH3BH3 FREQ.LOG.

The low frequencies are -6.4842 -4.4175 -0.0011 -0.0009 -0.0008 0.8459.

Energy comparison

E(NH3)= -56.55776872a.u. E(BH3)= -26.6153237196a.u. E(NH3BH3)= -83.22468907 a.u.

ΔE=E(NH₃BH₃)-[E(NH₃)+E(BH₃)]

ΔE=(-83.22468907)-[(-26.6153237196)+(-56.55776872)]

= -0.0516 a.u.

= -0.0516*2625.5 KJ/mol

= -135 KJ/mol

Schlenk Equilibrium

Considering the grignard reagent MeMgCl, the following species were analysed, excluding Me₂Mg and MgCl₂.

(1) MeMgCl

Optimisation

A mixture of basis sets were used. 6-31G(d,p) was used for the C and H atoms, while LanL2DZ was used for the Mg and Cl atoms. The log file for this optimisation is Media:JS Mg mix opt.log.

The optimised bond length for Mg-Cl is 2.26A^o and for Mg-Me is 2.07A^o. The optimised bond angle is 180.0^o.

	MeMgCl
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-55.769
Gradient/au	0.00000838
Dipole moment/D	3.13
Point group	C1
Time taken/s	68

        Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000396     0.001800     YES
 RMS     Displacement     0.000145     0.001200     YES
 Predicted change in Energy=-2.482616D-09
 Optimization completed.
    -- Stationary point found.

Frequency Analysis

This log file for this process is Media:JS MEMGCL FREQ.LOG‎.

Low frequencies ---  -17.8458   -3.0113   -0.0001   -0.0001    0.0002    4.3589

	MeMgCl
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-55.769
Gradient/au	0.00000843
Dipole moment/D	3.13
Point group	C1
Time taken/s	38

          Item               Value     Threshold  Converged?
 Maximum Force            0.000029     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000472     0.001800     YES
 RMS     Displacement     0.000199     0.001200     YES
 Predicted change in Energy=-3.505925D-09
 Optimization completed.
    -- Stationary point found.

Vibrations

Number	Vibration Form	Frequency	Intensity	Symmetry C_3v
1	The H move left and right in a concerted manner, as the B moves in the opposite direction. (bend)	97.8	35	E
2	The top two H move diagonally in the shown direction, at the same time, while the remaining B and H move slightly up and down. (bend)	98.2	35	E
3	The bottom H moves clockwise as the top two move anticlockwise. The B remains almost totally stationary. (bend)	357	11	A₁
4	The H move out in these directions in a concerted way. The B does not move. (stretch)	627	58	A₁
5	The top left H moves away from the B as the top right H is moving towards it. The B and the H remain almost completely still. (stretch)	627	104	E
6	The top two H move away from the B, as the other H moves towards it. The B remains almost totally motionless. (stretch)	627	104	E
7	The H move left and right in a concerted manner, as the B moves in the opposite direction. (bend)	3040	18	A1
8	The top two H move diagonally in the shown direction, at the same time, while the remaining B and H move slightly up and down. (bend)	3120	12	E
9	The bottom H moves clockwise as the top two move anticlockwise. The B remains almost totally stationary. (bend)	3120	12	E

(2) Me₂Mg₂Cl₂L₂, L = Et₂O

Optimisation

Here is the optimisation file Media:JS MG2 MIX ET2O OPT3.LOG

	MG2, L = ET2O
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-579.0039
Gradient/au	0.00000342
Dipole moment/D	9.51
Point group	C1
Time taken	1h 43min

         Item               Value     Threshold  Converged?
 Maximum Force            0.000010     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.000537     0.001800     YES
 RMS     Displacement     0.000115     0.001200     YES
 Predicted change in Energy=-2.800254D-09
 Optimization completed.
    -- Stationary point found.

Frequency

This is the frequency analysis file Media:JS Mg2 Et2O FREQ.log

	Mg2, L=Et2O
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-579.004
Gradient/au	0.00000343
Dipole moment/D	9.50
Point group	C1
Time taken	1h 8min 40s

Low frequencies ---   -4.2354    0.0005    0.0007    0.0008    4.7788    8.7652

Vibrations

Unfortunately, there were 120 generated vibrational modes for these molecules, making it difficult to analyse each mode individually. Therefore, only the key modes are shown, meaning the ones that involve the Mg and Cl atoms.

Number	Vibration Form	Frequency	Intensity	Symmetry if the structure was ideal C_2v
1	The two Cl move in and out, at the same time(symmetrically). (stretch)	47.3	0	A₁
2	The two Cl move up and down at the same time. (bend)	76.6	1	A₁
3	The Mg and the Cl move diagonally in a asymmetric fashion. (stretch)	103	2	A₁
4	The two Cl move up and down at the same time. (bend)	128	5	A₁
5	The two Cl move in as the two Mg atoms move out, symmetrically. (stretch)	189	2	A₁
6	Each Mg and Cl stretches symmetrically. (stretch)	218	2	A1
7	The two Cl stretch asymmetrically, as do the Mg, but in the opposite direction. (stretch)	284	50	A₂
8	Again, the two Cl stretch asymmetrically, as do the Mg, but in the opposite direction. (stretch)	287	85	A₂
9	The Mg and the Cl move in and out symmetrically, in a concerted manner. (stretch)	304	21	A₁

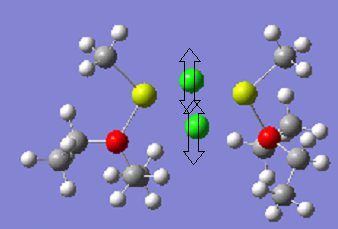
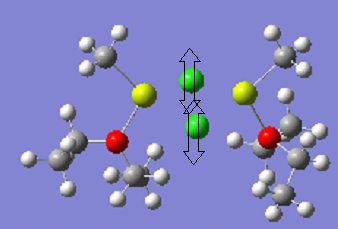
A key point to note, that is evidenced by the following spectra, as well as the population analysis, is that the diagram at the beginning of this section is only a very rough estimate of where the electrons actually lie. Specifically, there appears to be a high amount of electron density between the two Cl atoms. The term "bond" is not used here, due to the vagueness of its definition, discussed above. The modes 1, 5, 7 and 9 seem to show this. An advantage of using this program is that the symmetric stretches of Cl-Cl can still be viewed, despite the fact that they are not IR active, since they do not cause a change in the dipole of the molecule. These all have A₁ symmetry. Due to the fact that the frequency of the vibration is inversely proportional to the reduced mass, the Cl-Cl stretches and bends are at a low frequency. In addition, there seems to be a so called "bond" between the Mg and Cl atoms, shown by modes 2, 3, 4 and 6. Furthermore, mode 9 suggests the presence of a bond between the Mg atoms.

Comparing these modes to those for MeMgCl, they are very different, in terms of their frequencies, suggesting that the solvent molecule is interacting with the molecule quite profoundly. For instance, mode number 3 for MeMgCl has a frequency 250cm^-1 greater than mode number 3 for the one above, which is the same mode. This indicates that the Mg has become electron deficient. This is the only mode that can be compared fairly, based on the fact that the ligand is also affecting the reduced mass, as well as the force constant. Therefore, it is not a clear indication of the presence of electron density.

Molecular orbitals

This is the D-space for the population analysis.

Number	Energy/a.u.	Atoms involved	Orbitals That Are Overlapping
61(LUMO)	-0.02344	Cl + Mg	Probably p_x, p_y and p_z to give a δ bond.
60(HOMO)	-0.20946	Cl + Mg + C + H	p_x to form π bond. σ* between Mg and Me.
57	-0.29044	Cl	py to form π* bond.
56	-0.29731	Cl	p_y to form π bond.
53	-0.31822	Cl	p_x to form π* bond.
52	-0.32726	Cl	p_x to form π bond.
51	-0.32981	Cl	p_z to form σ bond.
47	-0.34083	Cl + Mg	p_z to form σ bond.
45	-0.3615	Cl + O + C + H	Explained below.
20	-0.75058	Cl	s to form σ* bond.
17	-0.76274	Cl	s to form σ bond.

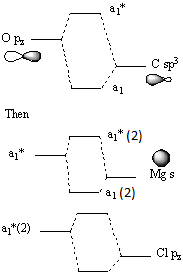
Molecular orbital 45 is the p_x orbital on Cl, overlapping with the Mg-O bond. Considering the C-O bond, it formed by the s orbital on the Mg mixing with an O orbital, since they are both have a₁ symmetry. The O orbital consists of an sp³ orbital on the C, mixing with the p_z orbital on the O.

The vast majority of these modes indicate that there is a reasonably large amount of electron density between the Cl atoms, that is, it could be said that there is a "bond" between them. Interestingly, energy level 45 shows that, in addition, the O can overlap with the central Mg and Cl atoms as well. Also, energy level 47 shows a high level of electron density between all of the central Mg and Cl atoms, as does the LUMO. This explains why the IR spectrum indicates the existence of Mg-Mg and Mg-Cl "bonds". Furthermore, the HOMO involves the central atoms, as well as the methyl group. The majority of the electron density is on the Me, since it is the C that is electronegative and acting as a nucleophile, shown in the NBO analysis below.

Natural Bond Orbital Analysis

This image of charge distribution is from -1.375 to 1.375, with green indicating positive charge.

Atom	Mean NBO charge
Mg	+1.280
C	-1.374
Cl	-0.654
O	-0.66

The C is the most electronegative atom, which can then act as a nucleophile in C-C bond forming reactions, as expected. The Mg is electropositive, stabilized by the electronegative O, which comes from the solvent.

Looking at the log file gives a significant amount of information about the central atoms.

1. (1.97330) BD ( 1)Mg   1 -Cl   3 
                (  5.76%)   0.2399*Mg   1 s( 23.62%)p 3.23( 76.38%)
                                            0.4858  0.0130 -0.5089 -0.0444 -0.1705
                                           -0.0157  0.6871  0.0388
                ( 94.24%)   0.9708*Cl   3 s( 30.28%)p 2.30( 69.72%)
                                            0.5503  0.0007  0.7286  0.0012  0.1048
                                            0.0005 -0.3942  0.0030
     2. (1.97364) BD ( 1)Mg   1 -Cl   4 
                (  5.93%)   0.2435*Mg   1 s( 24.67%)p 3.05( 75.33%)
                                            0.4965  0.0111 -0.4100 -0.0316 -0.2557
                                           -0.0247 -0.7184 -0.0467
                ( 94.07%)   0.9699*Cl   4 s( 30.58%)p 2.27( 69.42%)
                                            0.5530  0.0005  0.6706  0.0013  0.1856
                                            0.0007  0.4582 -0.0029
 4. (1.97265) BD ( 1)Mg   2 -Cl   3 
                (  5.89%)   0.2427*Mg   2 s( 24.73%)p 3.04( 75.27%)
                                           -0.4972 -0.0105 -0.4259 -0.0316  0.1065
                                            0.0117 -0.7460 -0.0471
                ( 94.11%)   0.9701*Cl   3 s( 29.52%)p 2.39( 70.48%)
                                           -0.5434 -0.0001  0.6809  0.0014 -0.0389
                                           -0.0002  0.4895 -0.0033
     5. (1.97283) BD ( 1)Mg   2 -Cl   4 
                (  5.74%)   0.2395*Mg   2 s( 23.67%)p 3.22( 76.33%)
                                           -0.4863 -0.0150 -0.5228 -0.0335  0.2379
                                            0.0185  0.6563  0.0343
                ( 94.26%)   0.9709*Cl   4 s( 29.49%)p 2.39( 70.51%)
                                           -0.5431 -0.0001  0.7394  0.0011 -0.1085
                                            0.0008 -0.3827  0.0028

Considering the Mg-Cl bonds, it is clearly a relatively accurate approximation to say that the Mg atoms are sp³ hybridised. This means that their ideal bond angle should be somewhere around 109^o. The fact that their average bond angles are actually 98.6^o and 122.9^o suggests that there is a significant amount of ring strain. This is obviously greater in the Mg3 molecule, which could be one reason why it is the least stable molecule. Looking at the Cl atoms, which constitute almost 95% of the bonds, they are all almost exactly 3:7 s:p orbitals. These would, again, prefer an angle of around 115^o. The fact that the internal angles are almost 90^o, again, suggests that a large amount of ring strain is present.

No Mg-Mg or Cl-Cl bonds are officially detected by Gaussian, due to the previously stated fact that it detects the existence of bonds based on the distances between the atoms. It is clear from the analysis that they can be said to exist, however.

(2) Me₂Mg₂Cl₂L₂, L = THF

Optimisation

This is the D-space for the optimisation.

	MG2, L = THF
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-576.581
Gradient/au	0.00017625
Dipole moment/D	10.41
Point group	C1
Time taken	4h 7min 46s

         Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000002     0.000300     YES
 Maximum Displacement     0.001290     0.001800     YES
 RMS     Displacement     0.000296     0.001200     YES
 Predicted change in Energy=-4.797915D-09
 Optimization completed.
    -- Stationary point found.

Frequency

Here is the D-space for the frequency analysis.

	MG2, L = THF
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-576.581
Gradient/au	0.00000763
Dipole moment/D	10.45
Point group	C1
Time taken	54min 20s

Low frequencies ---  -11.6009   -0.0004   -0.0004   -0.0003    2.8476    7.2269

Molecular orbitals

This is the D-space for the population analysis.

(3) Me₂Mg₂Cl₂L₂, L = THF

Optimisation

This is the D-space for the optimisation.

	MG2, L = THF
File type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-576.555
Gradient/au	0.00025064
Dipole moment/D	13.28
Point group	C1
Time taken	4h 26min 9s

         Item               Value     Threshold  Converged?
 Maximum Force            0.002152     0.000450     YES
 RMS     Force            0.000281     0.000300     YES
 Maximum Displacement     0.454039     0.001800     YES
 RMS     Displacement     0.110593     0.001200     YES
 Predicted change in Energy=-5.882623D-04

Frequency

This is the D-space for the frequency analysis.

	MG2, L = THF
File type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	Gen
Final energy/au	-576.559
Gradient/au	0.00001015
Dipole moment/D	11.41
Point group	C1
Time taken	4h 40min 59s

Molecular orbitals

This is the log file Media:JS Mg3 THF NBO.log and this is the checkpoint file Media:JS Mg3 THF NBO FINAL.fchk for the population analysis.

Energy Comparison

	Energy of Molecule/a.u.
Mg2, L = Et₂O	-579.0039
Mg2, L = THF	-576.581
Mg3, L = THF	-576.555

Looking at these values, it is clear that considering their absolute values in KJ/mol would be pointless, due to their magnitude. However, when the structures are viewed, they all look sensible. Therefore, their energies can be compared to each other.

Interestingly, Mg2 with L=THF is more stable than Mg3 with L=THF. This suggests that, overall, the intramolecular forces between the protons on the THF ligands and the methyl groups are attractive, and are lowering the energy of the molecule. Viewing the molecules below shows that the Mg3 molecule, shown , is trying to maximise this interaction. The , is already close to the optimum distance.

The shortest distance between the protons is 2.33A^o in the Mg molecule, but 2.67A^o in Mg2. However, Mg2 has many more of these interactions than Mg2. Presumably, the molecule with Et₂O ligands is the most stable due to the lack of ring strain. In addition, it is easier for molecule to form the H-H interactions.

MO Comparison

Number	MO	Energy Mg2, L=Et₂O/a.u.	Energy Mg2, L=THF/a.u.	Energy Mg3, L=THF/a.u.	Atoms involved	Orbitals That Are Overlapping
61(LUMO)		-0.02344	+0.02436	+0.02756	Cl + Mg	Probably p_x, p_y and p_z to give a δ bond.
60(HOMO)		-0.20946	-0.20707	-0.20541	Cl + Mg + C + H	p_x to form π bond. σ* between Mg and Me.

The orbitals of each molecule have almost identical geometry, therefore analysing the energy of these orbitals are key to understanding their chemistry. Based on this, the Mg2, L=Et₂O, is the best electrophile, from the fact that it has the lowest lying LUMO. Mg3, L=THF, is the best nucleophile, with its highest energy HOMO.

Conclusion

This particular grignard reagent is a reasonably reactive molecule. The reasons for this are numerous, and are shown clearly by the population analysis, with the Mg3 molecule being the slightly better nucleophile. This analysis also shows that both solvents stabilize the molecules, with Et₂O dong a slightly better job, shown by their relative energies. In addition, the population analysis shows explicitly what exactly is happening, in terms of bonding between the central atoms. Using molecular orbital theory, it was possible to explain what exactly was mixing in the majority of the key orbitals. As well as this, the vibrational analysis was in agreement with the population analysis and used to reinforce the data. The log file from the population analysis, in particular, was useful in analysing the position of the electron density between the central atoms. The two difficulties encountered were that, first, the Mg3, L=Et₂, molecule was not successfully generated. Second, the issue that Gaussian is unable to label the interactions between Mg-Mg and Cl-Cl as bonds.

References

↑ H. Ulrich and G Heyne, Physikal. Chem., 1941, B 49, 284

[1] H. Ulrich and G Heyne, Physikal. Chem., 1941, B 49, 284

[1]

Inorganic Computational Chemistry

Optimisation

BH3

3-21G

6-31G(d,p)

GaBr3

BBr3

Bond Length Comparison

Frequency Analysis

BH3

Vibration Visualisation

GaBr3

Vibration Comparison

BH3 MO Analysis

NH3 NBO Analysis

NH3BH3 Energy Minimum

Energy comparison

Schlenk Equilibrium

(1) MeMgCl

Optimisation

Frequency Analysis

Vibrations

(2) Me2Mg2Cl2L2, L = Et2O

Optimisation

Frequency

Vibrations

Molecular orbitals

Natural Bond Orbital Analysis

(2) Me2Mg2Cl2L2, L = THF

Optimisation

Frequency

Molecular orbitals

(3) Me2Mg2Cl2L2, L = THF

Optimisation

Frequency

Molecular orbitals

Energy Comparison

MO Comparison

Conclusion

References

BH₃

GaBr₃

BBr₃

BH₃

GaBr₃

BH₃ MO Analysis

NH₃ NBO Analysis

NH₃BH₃ Energy Minimum

(2) Me₂Mg₂Cl₂L₂, L = Et₂O

(2) Me₂Mg₂Cl₂L₂, L = THF

(3) Me₂Mg₂Cl₂L₂, L = THF