Rep:Mod:shaneomar3

Module 3

The Cope Rearrangement

The Cope rearrangement of 1,5-hexadiene, which is a [3,3]-sigmatropic shift, will be investigated in order to understand how to carry out a chemical reactivity problem in Gaussview. This will be carried out by looking for the low energy minima of the structure and then the transition state, which yields information about the preferred reaction mechanism.

Optimising the reactants and products

Summary of anti optimisation

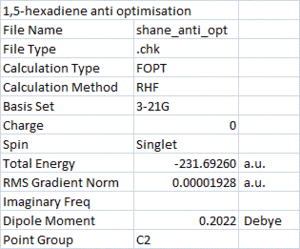
A molecule of 1,5-hexadiene with an "anti" linkage was built and cleaned in Gaussview before being optimized at the HF/3-21G level of theory. The result of this optimisation is shown on the right. The point group was found to be C₂.

Anti hexadiene optimised

Summary of gauche optimisation

Next, a molecule of 1,5-hexadiene with a "gauche" linkage for the central four C atoms was built and optimised in the same way. The result is shown on the right, the point group was also C₂.

Gauche hexadiene optimised

This gauche structure might be expected to be higher in energy than the anti (above), due to steric repulsion between -C=C groups. The results do indeed show that this gauche conformation is lower in energy by 0.67 kcal/mol. However, the distance between the -C=C groups is not small, so repulsion may not be an issue. There may be other electronic interactions which can explain the relative stability of these structures, which will be further explored.

Summary of gauche3 optimisation

One such stabilising interaction could be between the vinyl C-H and the other Pi bond, so called CH/Pi interaction. This interaction would be possible in the gauche structure optimised below (note the proximity of the vinyl H to the other C=C). The results of this optimisation are shown on the right.

Gauche3 hexadiene optimised

The results show that this is the lowest energy structure, which suggests the hypothesis was correct. On comparison with the table in 'Appendix 1', the structures optimised here can be identified as anti1, gauche4 and gauche3 respectively.

Summary of anti2 optimisation

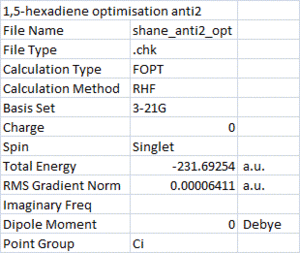
The Ci anti2 conformation of 1,5-hexadiene was then built and optimised using the HF/3-21G level of theory. The results are shown on the right, the optimised molecule below.

Anti2 hexadiene optimised

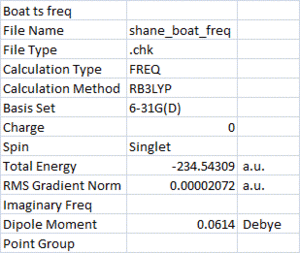
This structure has the same energy and symmetry (Ci point group) as the one given in the table and. Next, a higher level of optimisation was carried out: DFT/B3LYP, followed by a frequency analysis to check that the energy was a minimum. The results of the vibrational analysis showed that they were all positive and real, confirming the minimum. The lowest energy vibration is displayed below.

Summary of anti2 reoptimisation

Vibration

Sum of electronic and zero-point Energies= -234.469203 au

Sum of electronic and thermal Energies= -234.461856 au

Sum of electronic and thermal Enthalpies= -234.460911 au

Sum of electronic and thermal Free Energies= -234.500782 au

These values are identical to those give in the appendix which shows a good agreement.

Optimising the "chair" and "boat" transition structures

In order to calculate the activation energies for the cope rearrangement, the two possible transition structures were optimised in different ways. Both of these chair and boat transition structures consist of two allyl fragments and the structures were optimised using the following methods.

Summary of chair TS optimisation

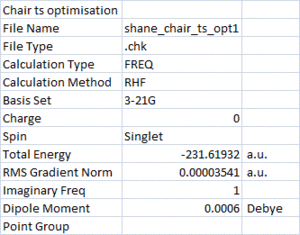
First, the chair TS structure was built in Gaussview by optimising the fragment at the HF/3-21G level of theory and placing the terminal ends of the allyl fragments roughly 2.2 Å apart. This "guess" structure was then optimised to a transition state (TS Berny). The reults of this optimisation are shown, with the imaginary vibration corresponding to the cope rearrangement shown below.

Vibration

Frozen bond optimisation

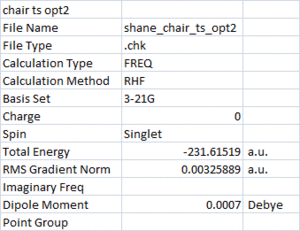
Next, the chair structure was optimised again using the frozen orbital method. Using the Redundant Coor Eidtor, the bonds between the two allyl groups were frozen at 2.2 Å. This structure was then optimised to a minimum, the results and structure are shown.

Hessian modified optimisation

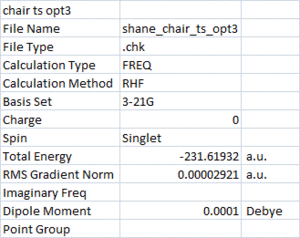
These bonds which are forming/breaking were then optimised (Hessian modified) without calculating the force constant. The resulting structure and summary are given below.

As the structures in the Jmol buttons show, the bond length (making/breaking) is 2.02 Å in the Hessian modified structure. This is 0.18 Å shorter than the frozen bond optimisation.

The boat transition structure was then optimised, firstly using the QST2 calculation. This involves building the reactant and product structures, and interpolating between the two to find the transition structure. The first attempt at this resulted in an error. The resulting clearly shows abnormal bonding as shown below:

First attempt boat optimisation

The cause of this error was due to the initial geometry used for the optimisation. In the QST2 method the reactant and product must be built to more closely resemble the transition structure in order for the calculation to work. The structures were rebuilt to more closely resemble a boat conformation, and the calculation repeated. This time the results were more reasonable, only one imaginary frequency was found. This represents the formation/breaking of the bonds and is shown below:

Boat optimisation QST2

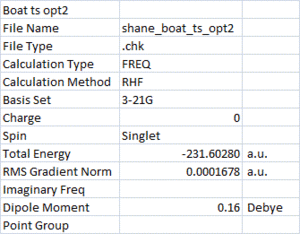
Vibration

In order to determine the conformer of 1,5-hexadiene that is involved in the cope rearrangemnt, an Intrinsic Reaction Coordinate method was used. This allows you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. 50 points were visualised in this calculation, but the last point caused the energy to increase so was not used. Instead, the last point on the IRC was taken and a normal minimization was run on it. The results of this are shown:

Chair IRC

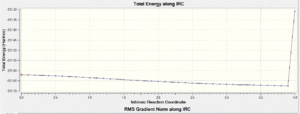
Optimised Chair from IRC

The energy and symmetry of this structure is a good match to the gauche2 structure in the appendix. This would suggest that the reaction paths from the transitions structures will lead to a gauche2 structure. This is quite surprising because there are lower energy conformers of 1,5-hexadiene. However, the gauche2 structure seems to be closest in energy to the transition structure.

Next, the chair and boat transition structures were optimised at the B3LYP/6-31G(d) level of theory, followed by frequency calculations with the same method. The purpose of this was to find the activation energies by looking at thermochemistry data.

Chair B3LYP/6-31G(d)

Boat B3LYP/6-31G(d)

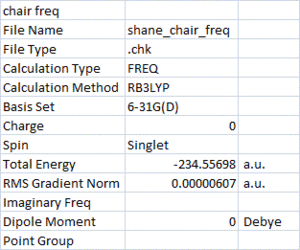
The geometry of the reactants and transition states optimised at the higher level are very close to those at the lower level of theory. The activation energies were calculated at 298.15^oK by assuming the gauche2 conformer is the one which proceeds the rearrangement in both chair and boat pathways. The energy difference (looking at 'sum of electronic and thermal energy') between reactant and transition state was used to find the activation energy.

The activation energies calculated at the lower level of theory were significantly larger than the activation energies using higher level of theory. Using HF/3-21G, the ΔE (Chair) was 44.21 kcal/mol and ΔE (Boat) was 54.29 kcal/mol. Whereas with B3LYP/6-31G(d), ΔE (Chair) was 32.60 kcal/mol and ΔE (Boat) was 40.76 kcal/mol.

These values show that the cope rearrangement is more likely to occur via the chair transition state, which is not surprising since it is the lower energy conformer. The values are a good match to those in the appendix, and the activation energies calculated a 0^oK are slightly lower than experimental values.

The Diels Alder Cycloaddition

Diels Alder cycloaddition

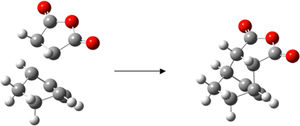
The Diels Alder reaction is a type of pericylcic reaction. The HOMO/LUMO of one reactant reacts with the HOMO/LUMO of the other, which is only allowed if the symmetry of the orbitals is suitable for them to interact. To investigate this type of reaction the transition states can be built and analysed to understand the MO and bond formation of the reaction.

Ethylene + Cis Cyclobutadiene

HOMO of cis-butadiene

LUMO of cis-butadiene

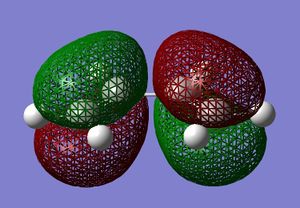
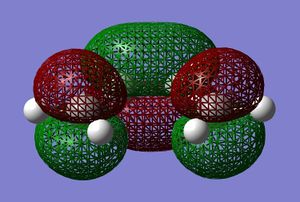
Cis-butadiene was built and optimised in gaussview using the AM1 semi-emperical molecular orbital method. The HOMO and LUMO were plotted and are displayed below.

These molecular orbitals can be classified as being either symmetric s, or antisymmetric a with respect to the plane of symmetry going though the middle of the molecule perpendicularly. For example, the HOMO of cis-butadiene is anti-symmetric and the LUMO is symmetric. The HOMO and LUMO of ethylene are the Pi and Pi* orbitals, which are s and a respectively. Therefore you would expect the HOMO and LUMO pairs to interaction in the Diels Alder reaction because the symmetries are suitable.

HOMO of transition state (a)

LUMO of transition state (s)

The transition state structure of the reaction was built and optimised using the same method as above. The partly formed C-C bonds were estimated as 1.6 Å in this optimisation. The MOs were plotted and are displayed on either side. The HOMO is antisymmetric and the LUMO is symmetric. This shows that the HOMO of the transition state was made from the overlap/interaction of the butadiene LUMO and ethylene HOMO. The LUMO transition state was made from the butadiene HOMO and ethylene LUMO. The orbitals are visually a good match to this description and also the symmetric and antisymmetric pair theory.

The geometry of the transition state can be viewed here:

The length of the partly formed C-C bonds is 2.12 Å (as shown in the Jmol Button). Typical sp³C - sp³C bond length is 1.54 Å, and sp²C - sp² bond length is 1.47 Å, so the partly formed bonds in this TS are much longer than a formed C-C bond. However, the Van der Waals radius of a carbon atom is 1.7 Å, which shows that there is definitely a bond being formed since the sum of the carbons' radii is 3.4 Å.

TS vibrations

Imaginary frequency	Lowest real frequency
Vibration	Vibration

The vibration that corresponds to reaction path at the transition state is displayed above. The formation of the two bonds is synchronous, whereas the lowest positive frequency is an asynchronous vibration.

Cyclohexadiene + Maleic Anhydride

Cyclohexa-1,3-diene reacts with maleic anhydride to give primarily the endo adduct. The reaction is thought to be kinetically controlled so that the exo transition state should be higher in energy.

The exo and endo transition states were built in gaussview with a guess of 2.1 Å for the partly formed bond distances. The structures were optimised using the semi empirical/AM1 method and the geometries are shown below:

Endo and Exo TS geometries

	Exo TS	Endo TS
Energy	-0.05050 hartree	-0.05159 hartree

The energy of the exo transition state is calculated as 0.68 kcal/mol higher than the endo TS. Therefore the hypothesis that the reaction is kinetically controlled appears to be confirmed. The geometries in the table above show that the partially formed bonds are roughly the same length in both transition states (the exo TS bonds are 0.01 Å longer than those in the endo TS). However, the -(C=O)-O-(C=O)- fragment in the exo TS is 2.94 Å from the "opposite" -CH2-CH2-, whereas in the endo the -(C=O)-O-(C=O)- is 2.89 Å from the "opposite" -CH2=CH2-. Since we are comparing a roughly planar alkene group to an alkane group, there may be more strain in the exo TS despite the longer distance from the -CH2-CH2- fragment. To investigate the effect this has on the energy of the transition state, the molecular orbitals of the structures must be considered.

Endo and Exo TS HOMOs

Angle	Exo HOMO	Endo HOMO
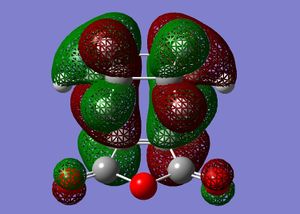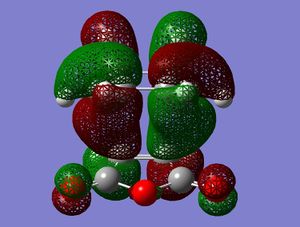HOMO front	Antisymmetric	Antisymmetric
HOMO side	No secondary orbital overlap	Secondary orbital overlap

This MO table shows the HOMOs of the two transition states from a front view and a side view. The side view of the endo TS shows quite clearly that the Pi-type orbitals of the -(C=O)-O-(C=O)- fragment are in close proximity to the Pi-type orbitals of the opposite ring, with a well matched symmetry. An overlap of electron density could be expected which would slightly lower the energy of the transition state. This is be described as a secondary orbital overlap effect. The exo TS does not have this interaction since the -(C=O)-O-(C=O)- fragment is on the other side of the molecule so does not overlap. This would explain the lower energy of the endo TS compared to the exo TS, hence why the endo product is formed.

This analysis has assumed that the reaction is kinetically controlled, which would mean the endo product is favoured. However, thermodynamic effects have been neglected in these calculations which means that the results do not necessarily rule out an exo product. Since these calculations are focused on the kinetic aspects (transition state energy), the possibility of thermodynamic control could not be taken into account. However, these results are a good match to experimental findings, therefore the calculations can be said to have been accurate.