Rep:Mod:sha
Module 2: Bonding (Ab initio and density functional molecular orbital)
Part I: Boron-Centered Small Molecules
BH3, Borane
Optimisation
BH3 was optimised(from an arbitary B-H bond length of 1.50Å) with quantum mechanical methods using Gaussian. The B3LYP(Becke-3-Parameter, Lee-Yang-Par) method and 3-21G basis set(a simple basis set)was used. B3LYP is a hybrid exchange correlation function( approximates exchange-correlation energy function in DFT(density functional theory)) which determines the type of approximation made in solving the Schrödinger equation. The relatively simple and inaccurate basis set(short optimisation time) was applied as BH3 is a small and symmetrical molecule hence calculation using this basis set is sufficient in obtaining accurate results. Large inaccuracies and errors will occur in the calculation of large or complicated molecules using this basis set. A summary of the optimisation is shown:
Log file output: Media:Wu_BH3_OPT.LOG
Optimised BH3
| File Type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | 3-21G |
| Charge | 0 |
| Spin | singlet |
| E(RB3LYP) | -26.4623 a.u. (-70189kJ/mol) |
| RMS Gradient Norm/a.u. | 0.00 |
| Dipole Moment/Debye | 0.00 |
| Point Group | D3H |
| Job cpu time /s | 26.0 |
| B-H Bond length /Å | 1.19 |
| HBH Bond angle/° | 120.0 |
The optimised bond length, bond angle and point group was found to be 1.19Å, 120.0° and D3H. This is in good agreement with theoretical and experimental observation from Hartman et al[1]: bond length =1.19Å, bond angle=120.0°, molecular geometry = trigonal planar, point group =D3H.
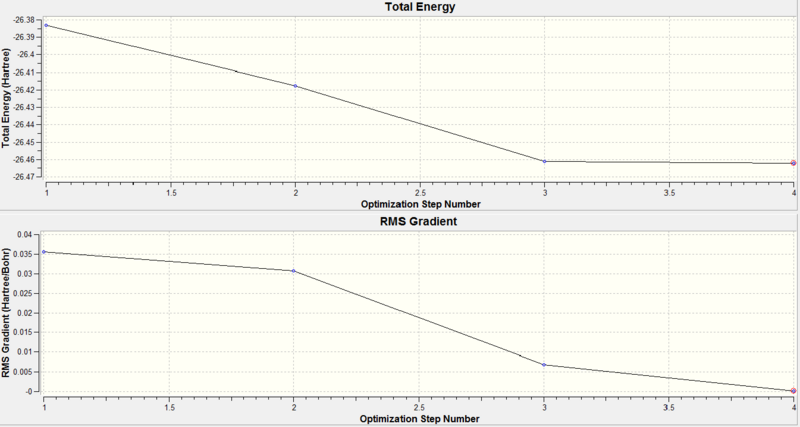
The optimisation plots are used to check the energy of the molecule has reached a minimum and the geometry has converged. The total energy against optimisation step number graph converges to a minimum and the RMS(Root Mean Square) gradient against optimisation step number graph converges to zero(turning point) as the minimum is approached. The energy of the molecule reach a minimum when the equilibrium position between atoms(optimal bond distances) are found where the positive potential energy(nuclear repulsion) is balanced by the negative potential energy(nuclear-electron attraction).
The equilibrium distance is found at the minimum point on the potential energy curve. The potential energy and force is related by F= -dE/dx. Therefore when the system is in equilibrium, we assume no net forces on the molecule and the gradient(first derivative of the potential energy with respect to the internuclear separation) of the potential energy curve is equal to zero.
Vibrational Frequency Analysis
Frequency analysis was performed on the optimised BH3 structure to confirm the minium structure was found. The vibrational modes are shown below and the IR(infrared) spectrum is also predicted.
Log file output: Media:YUTENG_BH3_FREQ.LOG
Vibration Modes and Frequencies
| No. | Mode of Vibration | Description | Frequency/cm-1 | Intensity | Symmetry (D3h) | Literature Frequency /cm-1[2] | |||
| 1 |
|
Out of plane wagging- concerted movement of all H atoms in and out of plane of screen, B atom moves slightly in the opposite direction. | 1144 | 93 | a2" | 1159 | |||
| 2 |
|
In-plane Scissoring- concerted movement of two H move in criss-cross fashion (scissors-like), B atoms moves slightly away from the two H atoms in the opposite direction, third H atom is stationary. | 1204 | 12 | e' | 1202 | |||
| 3 |
|
In-plane Rocking- The two bottom H's and B move(rock) concertedly in the plane as one unit while the top H moves with large amplitude. The top H moves left as the left H moves up and the right H moves down. | 1204 | 12 | e' | 1202 | |||
| 4 |
|
Symmetric Stretching- concerted movement of all three H's toward(then away from) central B atom in the BH3 plane, B atom is stationary. | 2598 | 0 | a1' | NA | |||
| 5 |
|
Asymmetric stretching- two bottom H's move in opposite directions, as one H moves away from B atom the other moves towards it with B wagging in the plane of the screen, the top H is stationary. | 2737 | 104 | e' | 2616 | |||
| 6 |
|
Asymmetric stretching- The top H moves towards(away) the central B atom as the other two H's move away (or opposite direction to the top H) in a concerted motion in the plane of the screen. B moves towards and away from the top H. | 2737 | 104 | e' | 2616 |
Predicted IR spectrum
Frequency analysis is essentially the second derivative of the potential energy surface, d2E/dx2 =k (rate of change of the restoring force with respect to distance). The frequency of a harmonic oscillator is proportional to the square root of k. The frequencies predicted are all positive confirming the structure of the molecule is a minima(minimum turning point) on the potential energy curve.
BH3 is a symmetrical molecule therefore 3N-6 vibrational modes (6) should be present (N = number of atoms). Indeed, 6 vibrational modes are observed in the computation. However, both the predicted and experimental IR spectrum show less peaks(3 peaks). This is due to degeneracy between vibrational modes 2 and 3 and between 5 and 6. Also vibrational mode 4 is not observed, this occurs as the IR spectrum measure changes in dipole moments generated by the vibrations, the 4th vibration mode in BH3 (D3h) involving the symmetric stretching of all 3 H atoms in and out of the stationary B centre has a change in dipole moment of zero(dipoles moments of individual stretches cancel each other out). Therefore the intensity of this stretch is zero(does not appear in spectrum) and the vibrational mode is non-IR active.
It was observed the deviation between computed and literature values is larger for high IR frequencies(asymmetric stretching) and smaller for low IR frequencies(wagging, Scissoring and rocking). This maybe due to the lager deviation from being a harmonic oscillator(not accounted for by Gaussian) in the asymmetric stretching.
Population Analysis (MO)
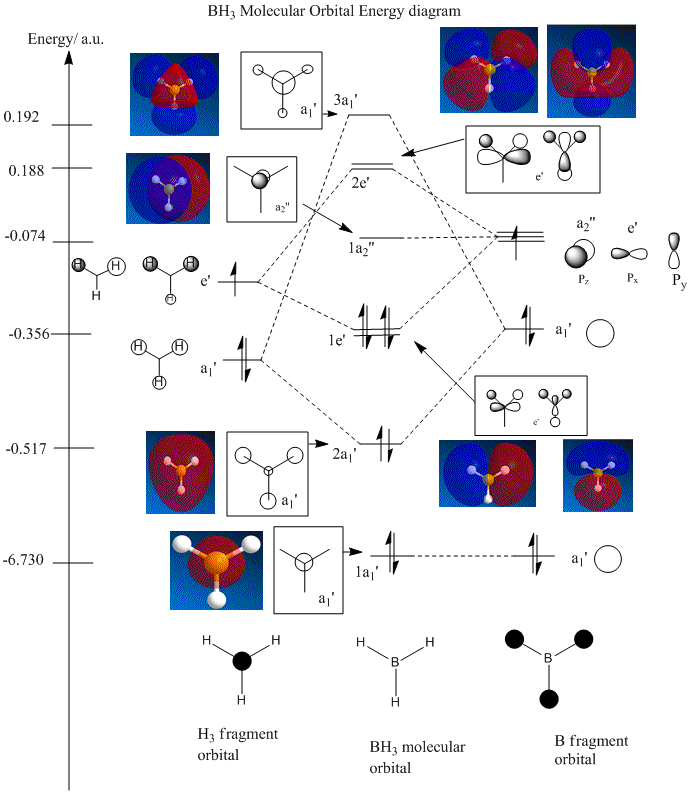
Population analysis was performed on BH3 with Gaussian to determine the molecular orbtials(MOs) of the molecule. With reference to Dr Patricia Hunt's 2nd year lecture course on MO theory, a qualitative MO diagram of trigonal planar D3h BH3 was constructed using Linear Combination of Atomic Orbitals(LCAO). The predicted Mos from Population analysis was included in the MO diagram to compare the results from the two different methods.
Data for MO/NBO (Energy):DOI:10042/to-6518
From the diagram, it can be observed the MO diagrams(MO shapes, phases and electron density) predicted from qualitative MO theory(LCAO) is in very good agreement with that calculated using Gaussian. The energy levels predicted using the two methods correlate reasonably well with the exception of the two highest energy levels(3a1' and 2e'). This is due to the major limitation of qualitative MO theory, where the exact energies and ordering of the molecular orbitals cannot be determined. The ordering of energy levels becomes uncertain when two non-degenerate MOs are close in energy, this is observed in 3a1' and 2e'. In the notes, MO theory places 3a1' orbital below the 2e' orbitals(no quantitative information about energies of orbitals so both arrangements are possible)by considering a1' energy levels are lower than e' and the strong s-s interaction in al' is not enough to raise 3a1' above 2e'. However, Gaussian results show the 3a1' orbital has slightly higher energy than 2e'. Moreover, the mixing of MOs will further complicate the ordering of energy levels using the MO theory. Therefore, MO theory is useful in predicting MO diagrams but Gaussian is more reliable at predicting the exact ordering of MOs when the MOs are close in energy.
TlBr3, Thallium Bromide
Optimisation
TlBr3 was optimised by Gaussian using B3LYP method with LanL2DZ basis set(medium level, involve pseudo-potentials). A medium level basis set was used instead of the simpler 6-311G(d,p)set as heavy atoms are involved, LanL2DZ uses D95V on first row atoms and Los Alamos ECP (pseudo-potential) on heavier elements. The symmetry of the molecule was constrained to a high tolerance (0.0001) to the D3h point group before optimisation.
Log file output:Media:Wu_TLBR3_OPTIMISATION.LOG
Optimised TlBr3
| File Type | .log |
| Calculation type | FOPT |
| Calculation method | RB3LYP |
| Basis set | LANL2DZ |
| Charge | 0 |
| Spin | singlet |
| E(RB3LYP) | -91.2181 a.u. (-241947kJ/mol) |
| RMS Gradient Norm/a.u. | 0.00 |
| Dipole Moment/Debye | 0.00 |
| Point Group | D3H |
| Job cpu time/s | 28.0 |
| Tl-Br Bond length/Å | 2.65 |
| Br-Tl-Br Bond angle/° | 120.0 |
The optimised bond length, bond angle was calculated to be 2.65Å and 120,0° (ideal angle for trigonal planar structure). This is in good agreement with the values reported by Glaser et al[3]: bond length = 2.52Å, bond angle = 120.0°. The small discrepancy in bond length maybe due to the conditions simulated by Gaussian being different to the experimental measurement methods.
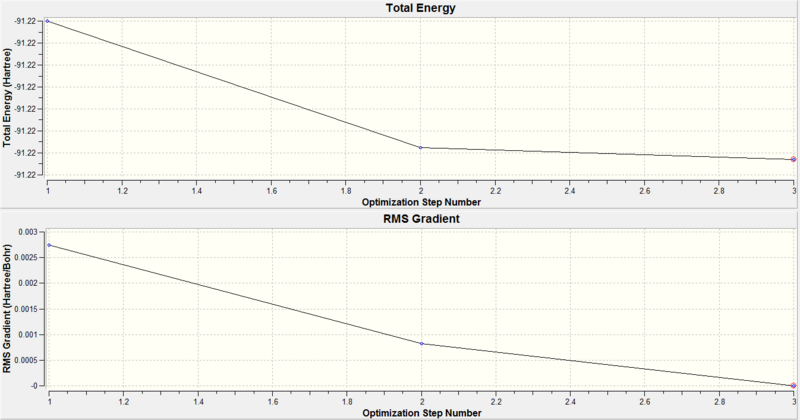
The optimisation plots confirm the energy of the molecule has reached a minimum and the geometry has converged. The total energy against optimisation step number graph converges to a minimum and the RMS(Root Mean Square) gradient against optimisation step number graph converges to zero as the minimum is approached.
Vibrational Frequency Analysis
The second derivative of the potential energy surface(frequency analysis) was carried out to confirm the optimised structure is a minima(minimum turning point) on the curve. Positive values confirm the minima whereas negative values show the maxima(transition state) is present.
The vibrational frequency analysis(essentially second derivative of energy optimisation) was carried out using the same method and basis set as the optimisation calculation. If the method or basis set was changed, it is apparent the the second derivative values would not reflect the initial potential surface and the results would not be comparable.
The "Low frequencies" for TlBr3 and the lowest "real" normal modes were obtained from the log file and quoted without altering decimal places.
Log file output:Media:YUTENG_TLBR3_FREQCORRECT.LOG
| Low frequencies cm-1 | lowest "real" normal Frequencies cm-1 |
|---|---|
| -3.4226 | 46.4288 |
| -0.0026 | 46.4291 |
| -0.0004 | 52.1449 |
| 0.0015 | |
| 3.9361 | |
| 3.9361 |
All the "real" normal frequencies are positive confirming optimised structure is a minima on the potential energy curve. The "low frequencies" are not normal modes, all the values are very close to zero and are only negative because of numerical difficulties indicating the method and basis set used for frequency analysis is satisfactory.
The vibrational modes are shown below and the IR spectrum is also predicted:
| No. | Mode of Vibration | Description | Frequency/cm-1 | Intensity | Symmetry (D3h) | |||
| 1 |
|
In-plane Scissoring- the two bottom Br atoms move in criss-cross fashion, Tl and top Br atom move(slightly)as an unit away(opposite direction) from the two bottom Br's. | 46 | 4 | e' | |||
| 2 |
|
In-plane rocking- The two bottom H's and B move(rock) concertedly in the plane as one unit while the top H moves with large amplitude. The top H moves left as the left H moves up and the right H moves down. | 46 | 4 | e' | |||
| 3 |
|
In-plane Rocking- The two bottom Br's and Tl move(rock) concertedly in the plane as one unit while the top Br moves with larger amplitude. The top Br moves right as the left Br moves down and the right Br moves up. | 52 | 6 | a2" | |||
| 4 |
|
Symmetric Stretching- concerted movement of all three Br's toward(then away from) central Tl atom in the TlBr3 plane, Tl atom is stationary. | 165 | 0 | a1' | |||
| 5 |
|
Asymmetric stretching- two bottom Br's move in opposite directions, as one Br moves away from Tl atom the other moves towards it with Tl wagging in the plane of the screen, the top Br is stationary. | 211 | 25 | e' | |||
| 6 |
|
Asymmetric stretching- The top Br moves towards(away) the central Tl atom as the other two Br's move away (or opposite direction to the top H) in a concerted motion in the plane of the screen. Tl moves towards and away from the top Br. | 211 | 25 | e' |
Predicted IR spectrum
TlBr3 is a symmetrical molecule therefore 3N-6 vibrational modes (6) should be present (N = number of atoms). Indeed, 6 vibrational modes are observed in the computation.
Chemical Bonds
In some structures gaussview does not draw in the bonds where we expect. This does not mean the bond does not exist. Gaussview have a set of pre-defined parameters that describe a bond, it has a maximum value for bond length in order for a 'bond' to be recognised as a 'bond'. If the calculated bond length is greater than the pre-assigned maximum value, gaussview does not draw in the bonds but the bonding interactions between are atoms are certainly present(confirmed by the presence of vibrational frequencies).
A chemical bond is an interaction between atoms or molecules which results in the formation of chemical substances that contain two or more atoms. These interactions include ionic, covalent, dipole-dipole, van der Waals forces and hydrogen-bonding. More simply, bonding is caused by the electromagnetic force attraction between opposing charges, either between electrons and nuclei, or a result of dipole moments.
Part II: an organometallic Complex
Cis-Trans isomers of Mo(CO)4(PCl3)2
Optimisation
The structures of cis- and trans- Mo(CO)4(PCl3)2 were optimised using Gaussian with B3LYP method. Initially, a low level pseudo potential/basis set LANL2MB was used with the "opt=loose" criteria. This optimises the molecule to a structure that is close to the minimal energy(rough geometry), good bond lengths and angles are found but the dihedral angles will not be well described. Subsequently, the structures were optimised a second time with LANL2DZ basis set(key words "int=ultrafine scf=conv=9") which provides an higher level optimisation(much better basis set and pseudo-potential ) than LanL2MB due to its high accuracy pseudo-potential with tight convergence. Therefore, LANL2DZ is more suited for the optimisation of this large complex with heavy atoms. A summary of the two optimisations are shown:
Mo(CO)4(PCl3)2 optimisation - LANL2MB basis set
| cis Mo(CO)4(PCl3)2 | trans Mo(CO)4(PCl3)2 | |
|---|---|---|
| File type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2MB | LANL2MB |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RB3LYP) | -617.5252 a.u.(-1637923kJ/mol) | -617.5221 a.u.(-1637915kJ/mol) |
| RMS Gradient Norm /a.u. | 0.00 | 0.00 |
| Dipole Moment/ Debye | 8.46 | 0.00 |
| Point Group | C1 | C1 |
| Job cpu time | 11 minutes 18.8 seconds | 7 minutes 22.0 seconds |
| D-space link | DOI:10042/to-6688 | DOI:10042/to-6687 |
Mo(CO)4(PCl3)2 optimisation - LANL2DZ basis set
| cis Mo(CO)4(PCl3)2 | trans Mo(CO)4(PCl3)2 | |
|---|---|---|
| File type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| Charge | 0 | 0 |
| Spin | Singlet | Singlet |
| E(RB3LYP) | -623.5771 a.u. (-1653976 kJ/mol) | -623.5760 a.u. (-1653973 kJ/mol) |
| RMS Gradient Norm/a.u. | 0.00 | 0.00 |
| Dipole Moment/Debye | 1.31 | 0.31 |
| Point Group | C1 | C1 |
| Job cpu time | 1 hour 10 minutes 43.6 seconds | 49 minutes 7.1 seconds |
| D-space link | DOI:10042/to-6689 | DOI:10042/to-6690 |
The optimised energy of the cis isomer (-1653976 kJ/mol) is 3 kJ/mol lower than the trans isomer (-1653973 kJ/mol). However the calculated energies have an error of ≈ 10 kJ/mol, therefore the calculations are not reliable enough in determining which isomer is more stable. Both isomers can be isolated experimentally where the trans-isomer is the thermodynamic product while the cis-isomer is the kinetic product. The trans isomer is reported to be lower in energy in the literature[4], this can be rationalised by the following reasons. The sterically bulky PCl3(or more bulky PPh3) groups are separated further apart in the trans-ismoser therefore relieving the high steric strain; the trans-isomer has a much lower dipole moment(0.30) compared to the cis isomer(1.31) which stabilises the molecule further, the dipole moment of the trans-isomer is low(close to zero) as the dipole moments of substituents cancel each other out due to their geometrical orientations.
Changes can be made to the ligand L=PR3 that would alter the relative ordering of the cis and trans isomers. The stability of the trans-isomer can be increased with respect to the cis-isomer by using more bulky PR3 ligands(e.g R=Ph3), this destabilises the cis isomer(increases in steric clash between Ph3) and the relief in steric strain observed in the trans-isomer becomes more significant. A more electronegative PR3 group e.g(R=F, instead of R=Cl) would increase the dipole moment and destabilise the cis- isomer, therefore the difference in stability between the isomers would increase with the trans-isomer being more stable.
The bond lengths and bond angles of cis and trans- Mo(CO)4(PCl3)2 (optimised geometry) were compared with that reported by Hogarth et. al[5] (obtained from X-ray crystallography) for cis and trans- Mo(CO)4(PPh3)2.
trans and cis- Mo(CO)4(PCl3)2 bond lengths and angles
| trans isomer | cis isomer | |||
| Gaussian Calculated value | Literature value | Gaussian Calculated value | Literature value | |
|---|---|---|---|---|
| Mo - P / Å | 2.44 | 2.500 | 2.51 | 2.58 |
| Mo - C / Å | 2.06 | 2.005 | - | - |
| P - Cl (P-C in lit.)/ Å | 2.24 | 1.828 | - | - |
| C - O / Å | 1.17 | 1.164 | - | - |
| P-Mo-P /° | 177.4 | 180.0 | 94.2 | 104.6 |
| P-Mo-C /° | 91.3, 90.0, 90.0 | 87.2 | - | - |
| trans - C-Mo-C /° | 180.0, 179.0 | 180.0 | - | - |
| cis- C-Mo-C /° | 90.5, 89.5 | 92.1 | - | - |
The results computed by Gaussian correspond well with experimental observation showing the optimised structure closely resemble the structure obtained from synthesis. This also shows the substitution of the Cl for Ph on the P centre did not affect the structure of the molecule greatly.
The calculated and experimentally observed Mo-P bond length for the cis-isomer is longer than the trans isomer, this is because the Mo-P bonds in the cis-isomer are elongated in order to minimise unfavourable non-bonding interactions between the relatively bulky Ph or Cl substituents. The P-Mo-P bond angle for the cis isomer was calculated to be 10° less than the experimental value, this difference may suggest the lowest energy structure of the molecule(global minimum) was not calculated(the minimum found(shown by vibrational analysis) is likely to be a local minimum) and perhaps another basis set or pseudo potential could be used to produce a more accurate prediction.
The bond lengths and angles for equatorial and axial positions are slightly different in the Gaussian calculations, this is reasonable as the geometry of molecule distorts from the ideal octahedral structure due to the steric strain caused by the bulky PPh3 or PCl3 ligands.
Vibrational Frequency Analysis
Frequency analysis was carried out to confirm the optimised geometry is a minimum. All positive values were obtained showing the minimum was found successfully.
Low Frequencies
Vibrations that have a very low frequency are summarised:
cis Mo(CO)4(PCl3)2 Vibrational Modes and Frequencies
Data : DOI:10042/to-6691
| Cis Mo(CO)4(PCl3)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| No. | Mode of Vibration | Description | Frequency/ cm-1 | Intensity | Symmetry (C1) | |||
| 1 |
|
Rocking - The three Cl atoms on each P atom rock as an unit with respect to the MO(CO)4, the movement of the two units are out of phase. The Mo(CO)4 unit moves slightly(almost stationary) | 11 | 0.03 | a | |||
| 2 |
|
The three Cl atoms on each P atom rock as an unit with respect to the MO(CO)4, the movement of the two units are out of phase. The Mo(CO)4 unit moves slightly(almost stationary) | 18 | 0.007 | a | |||
trans Mo(CO)4(PCl3)2 Vibrational Modes and Frequencies
Data : DOI:10042/to-6692
| Trans Mo(CO)4(PCl3)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| No. | Mode of Vibration | Description | Frequency/ cm-1 | Intensity | Symmetry (C1) | |||
| 1 |
|
The two PCl3 units rock in phase with respect to each other and out of phase with respect to rocking of the Mo(CO)4 unit | 5 | 0.09 | a | |||
| 2 |
|
The three Cl atoms on each P atom rock as an unit with respect to the MO(CO)4, the movement of the two units are out of phase. The Mo(CO)4 is stationary | 6 | 0 | a | |||
These low frequency vibrations are due the molecule rocking at low amplitude , low energies are required to cause these vibrations(energy is proportional to the frequency E=hf). Therefore these vibrations are likely to occur at room temperature.
C=O Stretching Frequencies
Carbonyl stretches from calculated using Gaussian are compared with literature[6] experimental values
C=O Carbonyl Vibration Frequencies in Cis-Mo(CO)4(PCl3)2
| Gaussian IR Frequency /cm-1 | Gaussian Intensity | Literature IR Frequency/cm-1[6]
|
Symmetry | IR spectrum |
| 2023 | 598 | 2072 | A1 | 
|
|---|---|---|---|---|
| 1958 | 633 | 2004 | A1 | |
| 1949 | 1499 | 1994 | B2 | |
| 1945 | 763 | 1986 | B2 |
C=O Carbonyl Vibration Frequencies in Trans-Mo(CO)4(PCl3)2
| Gaussian IR Frequency /cm-1 | Gaussian Intensity | Literature IR Frequency/cm-1[6]
|
Symmetry | IR spectrum |
| 2031 | 4 | N/A | A1g | 
|
|---|---|---|---|---|
| 1977 | 1 | N/A | B1g | |
| 1951 | 1467 | 1896 | Eu | |
| 1950 | 1476 | 1896 | Eu |
The results show the number of peaks computed and the frequencies at which they occur correspond well with literature value. The discrepancies in the stretching frequencies are due to Gaussian being not good treating π-backbonding and lack of anharmonicity terms in the calculation(10% error).
A total of 4 C=O stretches were predicted by theoretical calculation for both isomers. For the cis-isomer all 4 vibrational modes are seen in the infrared spectrum (IR-active), this is due to the change in overall dipole moment of molecule as a result of the stretches. Whereas for the trans-isomer, two vibrational modes are not observed experimentally. The A1g and B1g stretches are non-IR active(intensity = 0) as they do not result in an overall change in dipole moment, explaining the absence of these two peaks in the spectrum. The two Eu vibrational modes are degenerate and appears as one peak in the IR spectrum. Overall, the results show Gaussian is able to predict vibrations that are present in molecule which are not observed experimentally.
Part III: Mini Project
Introduction: Interhalogen compounds
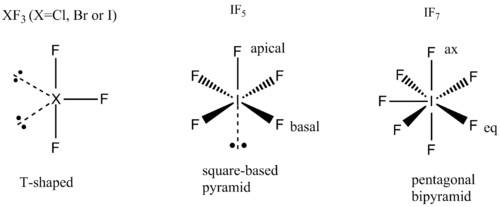
The relative energies, bond lengths, bond angles and molecular orbitals of the fluoride interhalogens are investigated using computational techniques in order to rationalise the reactivity and Lewis-acidic behaviour of the compounds. Interhalogen compounds investigated here include ClF3, BrF3, IF3, IF5 and IF7. Experimentally, these compounds are all prepared by direct combination of elements, the outcome of the reactions are controlled by temperature and pressure when more than one product possible[7].. In general, increased temperatures favour higher oxidation states of X(X=central halogen atom) and the highest oxidation states for X reached follows the order Cl < Br <I. The structural families are consistent with the VSEPR model. ClF3, BrF3and IF3 adopts T-shaped structures; IF5 have square-based pyramid stucture; IF7 adopts a pentagonal bipyramid structure.
Optimisation
The optimisation of all the compounds are summarised below. The B3LYP method was used for all the optimisations but different basis sets were used as some molecules contained heavy atoms. ClF3 does not contain any heavy atoms therefore a simple 6-31G(d) basis (pseudo potentials not required, confirmed with demonstrator) was used. Whereas for BrF3, IF3, and IF7, the Br and I are heavy atoms and must be treated pseudo potentials. There these are optimised with the "GEN" basis set selection and keywords "pseudo=cards gfinput", the input files were edited so that Br and I are treated with LANL2DZ(pseudo potentials) basis set and F is treated as 6-31G(d)(normal) basis set. However, an error message was experienced when optimising IF7 using this method("GEN" basis set selection) and the LANL2DZ basis set was used instead where all atoms are considered as heavy(confirmed with demonstrator). The structure of the molecules were adjusted close that of the literature(predicted using VSEPR) prior to optimisation, therefore Gaussian is more likely to find the global minimum rather than a local minimum.
Subsequent analyses (vibrational frequency, natural bond orbital/population analysis) of the same compound were performed using the same basis set to reflect the initial potential surface therefore yielding results that are comparable. Ideally, the same basis set should by used for all compounds to give better energy comparison as the energy generated by optimisation is very subjective and dependent on the method/basis set used.
| ClF3 | BrF3 | IF3 | IF5 | IF7 | |
| Data link | Media:Wu OPT CLF5.LOG | Media:WU BRF3 OPT.LOG | Media:WU IF3 OPTPP.LOG | Media:WU IF5 OPT.LOG | Media:WU IF7 OPTLANDZ.LOG |
| structure | |||||
| File type | .log | .log | .log | .log | .log |
| Calculation type | FOPT | FOPT | FOPT | FOPT | FOPT |
| Calculation method | RB3LYP | RB3LYP | RB3LYP | RB3LYP | RB3LYP |
| Basis set | 6-31G | Gen | Gen | Gen | LANL2DZ |
| Charge | 0 | 0 | 0 | 0 | 0 |
| Spin | singlet | singlet | singlet | singlet | singlet |
| E(RB3LYP)/a.u | -759.3703 | -312.4445 | -310.7462 | -510.3620 | -709.9516 |
| E(RB3LYP)/kJ mol-1 | -2014154 | -828728 | -824223 | -1353684 | -1883075 |
| Dipole moment/Debye | 1.29 | 1.51 | 2.81 | 3.17 | 11.65 |
| Point group | CS | CS | CS | CS | C1 |
| Job cpu time | 41.0sec | 54.0sec | 1min 0.0sec | 1min 50.0sec | 13min 48.0sec |
The point group for all the interhalogen compounds were calculated to be CS expect for symmetric pentagonal bipyramidal IF7 structure which belongs to the C1 point group.
Bond length and bond angles
The bond lengths and bond angles of interhalogens were compared with that reported in the literature[8].
bond lengths and angles of the compounds (X= central halogen)
| ClF3 | BrF3 | IF3 | IF5 | IF7 | ||||||
| Gaussian Calculated value | Literature value | Gaussian Calculated value | Literature value | Gaussian Calculated value | Literature value | Gaussian Calculated value | Literature value | Gaussian Calculated value | Literature value | |
|---|---|---|---|---|---|---|---|---|---|---|
| X-F / Å | 1.79(eq),1.87(ax) | 1.60(eq), 1.70(ax) | 1.80(eq), 1.87(ax) | 1.72(eq), 1.81(ax) | 1.88(eq), 1.94(ax) | 1.87(eq), 1.98(ax) | 1.88(basal), 1.83(apical) | 1.87(basal), 1.85(apical) | 1.99(eq), 1.94(ax) | 1.86(eq), 1.79(ax) |
| F-X-F / ° | 85.99 | 87.5 | 84.28 | 86 | 81.67 | - | 81.22(eq,ax), 88.61(eq,eq) | ~90 | 89.69(eq,ax), 71.99(eq,eq) | 90.0(eq,ax),72.0(eq,eq) |
The results computed by Gaussian correspond closely with experimental observation showing the optimised structure closely resemble the structure obtained from synthesis.
Upon increase in oxidation state of I atom(from IF3 to IF7), it can be observed the equatorial/basal I-F bond length increases. This is due to the increase in repulsive electronic interaction(or steric hindrance) between the equatorial/basal F atoms as the F-I-F angles become smaller on going from IF3 to IF7, therefore the bond length increases to reduce the repulsive interactions.
For IF3, IF5 and IF7 the equatorial/basal bond lengths are always larger than the axial/apical bonds, this is also due to the higher repulsive electronic interaction experienced by the equatorial/basal bonds which increases their length. For ClF3, BrF3 and IF3 the axial bond lengths are always larger than the equatorial, this is due the large repulsive electronic interaction between the axial X-F bond and the two lone pair of electrons. The axial bonds are closer to the lone pair therefore experiences larger repulsion resulting in increased bond length.
The equatorial-axial F-I-F angles on going from IF5 to IF7 does not vary greatly, the angles are all close to 90° which is in agreement with the literature structure. The IF3 is smaller than 90° due to the bent-T structure caused by the electron lone pairs. The equatorial-equatorial F-I-F angles decreased on going from IF3 to IF7 is clearly due to the increase in atom number in the equatorial plane.
The bond angle between axial and equatorial fluorides is relatively constant compared to the equatorial-equatorial bond angle as the apical fluoride usually stays in the same place while the equatorial rotates around to allow another fluoride into the molecule. The bond angles are less accurate compared to the predicted bond length, this may due to insufficient basis set being still insufficient.
Vibrational Frequency Analysis
Frequency analysis was carried out to confirm the optimised geometry is a minimum. All positive values were obtained showing the minimum was found successfully for all the compounds(see checkpoint files below), the input files were edited(before calculation) in the same way as for optimisation in order to use the "GEN" basis set. The vibrational modes for ClF3 are shown in detail here:
Vibration Modes and Frequencies of ClF3
| No. | Mode of Vibration | Description | Frequency/cm-1 | Intensity | |||
| 1 |
|
In-plane Scissoring | 201 | 16 | |||
| 2 |
|
Out of plane wagging | 236 | 23 | |||
| 3 |
|
In-plane Rocking | 291 | 1 | |||
| 4 |
|
Asymmetric stretching | 464 | 2 | |||
| 5 |
|
Asymmetric stretching | 631 | 15 | |||
| 6 |
|
Asymmetric stretching | 682 | 210 |
The vibrational modes and frequencies of ClF3, BrF3 and IF3 are tabulated below to allow comparison:
comparison between Vibration Modes and Frequencies of ClF3, BrF3 and IF3
| No. | Mode of Vibration | ClF3(Media:YUTENG CLF5 FREQ.LOG ) | BrF3(Media:WU BRF3 FREQ.LOG ) | IF3(Media:WU IF3 FREQ.LOG ) | |||
| Frequency/cm-1 | Intensity | Frequency/cm-1 | Intensity | Frequency/cm-1 | Intensity | ||
|---|---|---|---|---|---|---|---|
| 1 | In-plane Scissoring | 201 | 16 | 218 | 18 | 213 | 22 |
| 2 | Out of plane wagging | 236 | 23 | 225 | 21 | 189 | 22 |
| 3 | In-plane Rocking | 291 | 1 | 323 | 3 | 306 | 6 |
| 4 | Asymmetric stretching | 464 | 2 | 519 | 1 | 530 | 0 |
| 5 | Asymmetric stretching | 631 | 15 | 613 | 18 | 601 | 22 |
| 6 | Asymmetric stretching | 682 | 210 | 595 | 197 | 557 | 151 |
Frequency data files for IF5:Media:WU IF5 FREQ.LOG and IF7:Media:WU IF7 FREQ.LOG
Frequency analysis is essentially the second derivative of the potential energy surface, the frequencies predicted are all positive confirming the structures of all three molecules are a minimums(minimum turning point) on the potential energy curve.
6 vibrational modes were observed following the 3N-6 vibrational modes rule (N = number of atoms). Indeed, 6 vibrational modes are observed in the computation. One of the Asymmetric stretching modes in IF3 is not observed in the IR spectrum due to no change in dipole moments(intensity=0, non-IR active)
The same modes of vibrations were observed for all three complexes, their frequencies differed slightly. The vibrational modes closely resemble that seen for BH3 and TlBr3. However, the symmetric stretch mode is not present in the inter-halogen compounds as symmetry is lost due to the bent T-shaped structure.
Molecular Orbitals
The molecular orbitals (HOMO-1, HOMO, LUMO and LUMO+1) for IF3, IF5 and IF7 are compared and analysed. Again, the input files were edited(before calculation) in the same way as for optimisation in order to use the "GEN" basis set.
| orbital | HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|---|
| diagram |  |
 |
 |
 |
| Energy/ kJ/mol | -954 | -784 | -322 | -134 |
From the Mos it is clear that in the LUMO, I atom has a large un-occupied orbital below the plane atom. The HOMO show addition of electron density on the apical F atom compared to HOMO-1, more importantly the occupied I orbitals are largely in the plane of the atom and between I-F bonds. Therefore it can be deduced that IF3 is a better lewis acid than lewis base, because the un-occupied orbitals on I are very accessible for attack by a lewis base whereas the occupied orbitals are not accessible for attacking a lewis acid.
| orbital | HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|---|
| diagram |  |
 |
 |
 |
| Energy/ kJ/mol | -1086 | -971 | -205 | -144 |
The MOs show the IF5 compound is less prone to attack by a lewis base. The large un-occupied orbital below the plane I atom is still present but there is also a large occupied I orbital in the HOMO that lie below the plane, this occupied orbital will repel incoming electron pair from the lewis base thus decreasing the reactivity of IF5 towards lewis bases.
| orbital | HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|---|
| diagram |  |
 |
 |
 |
| Energy/ kJ/mol | -1237 | -1163 | -885 | -470 |
In IF7, the open area below the I atom is now occupied with another axial F atom. The structure forms a closed shell, and the central I atoms is not accessible to lewis base attack due to steric hindrance. Therefore IF7 is the most unreactive compound due to lack of any accessible orbitals and full valance shell.
NBO/Charge Distribution
The NBO/Charge Distribution of the interhalogens are compared and analysed:
Comparing the relative natural charge of the atoms (X = central halogen)
| compound | natural charge | ||
| X | F | Data file | |
|---|---|---|---|
| ClF3 | 0.935 | -0.353(ax), -0.230(eq) | Media:Wu CLF MO.LOG |
| BrF3 | 1.306 | -0.471(ax), -0.364(eq) | Media:WU BRF3 MO.LOG |
| IF3 | 1.562 | -0.545(ax), -0.471(eq) | Media:Wu IF3 MOFINAL.LOG |
| IF5 | 2.568 | -0.484(apical), -0.521(basal) | Media:Wu IF5 MO.LOG |
| IF7 | 2.533 | -0.347(ax), -0.368(eq) | Media:Wu IF7 OPTLANDZ MO.LOG |
Upon going from ClF3 to IF3, an expected increase in positive charge on the central atom is seen as the central atom is increasingly more polarisable due to more diffuse orbitals. Conversely to the central atom, the charge on the ax/eq fluoride becomes increasingly negative.
The eq/ax F atoms, show a trend of decrease in charge(more positive) upon increase in coordination from IF3 to IF7, this can be rationalised by the decrease in bond order as the same number of electrons are shared between increasing number of centres. For IF3 - eq F atoms to central I atom =3c-4e bond ; F5 =4c-6e bond; IF3 =6c-10e bond.
With the addition of F atom from IF3 to IF5, trend of increasing positive charge on the central I atom was observed due more electronegative F atoms withdrawing electron density away from the central atom. However, a slightly lower charge was seen for the I atom in IF7.
Dipole moment
The calculated dipole moments were compared to the literature[9]. and realated to the boiling points :
| Compound | Calculated Dipole Moment/Debye | literature Dipole Moment/Debye | literature boiling point/oC |
|---|---|---|---|
| ClF3 | 1.29 | 0.6 | 285 |
| BrF3 | 3.98 | 1.19 | 399 |
| IF3 | 1.62 | - | 245 |
| IF5 | 3.42 | 2.18 | 378 |
| IF7 | 0.029 | - | 278 |
The calculated dipole moments are generally higher than the literature. However, the trend is consistent and relates well with the boiling points. It was clearly observed that large dipole moments results in higher boiling points due to stronger attractive intermolecular interactions(dipole-dipole).
Relative Total Energy
The relative total energy of the compounds are compared below:
| Compound | Total energy/a.u. | Total energy /kJ mol-1 |
|---|---|---|
| ClF3(6-31G(d)) | -759.3703 | -2014154 |
| BrF3 | -312.4445 | -828728 |
| IF3 | -310.7462 | -824223 |
| IF5 | -510.3620 | -1353684 |
| IF7 | -709.9516 | -1883075 |
| ClF3(LANL2DZ) | -314.2272 | -833456 |
data file for ClF3(LANL2DZ): Media:Wu CLF3 OPT LANDZ.LOG
The total energy of ClF3 is much larger(more than x2) than the other two XF3 compounds, this is likely due to the different basis set used causing the energies to differ by a large amount. Therefore another optimisation was carried out for ClF3 using the LANL2DZ basis set, this yielded an energy much closer to the other two XF3 compounds and the results can be compared.
Upon increase in oxidation states from IF3 to IF7, the energies become more negative indicating the compounds are more thermodynamically stable. This is good agreement with the literature where an increase temperatures favours higher oxidation states of I(thermodynamic product).On going from ClF3 to IF3, the energies also become more negative indicating the compounds become more thermodynamically stable down the group. This may due to the decrease in electronic repulsions between the F atoms as the central atom X becomes larger.
Conclusion
The investigation into the chemical and physical properties of interhalogen compounds using computational techniques gave promising results. The bond length, bond angles, vibrational modes,Dipole moments, Relative Total Energy and NBO/Charge Distribution were all predicted with reasonable accuracy. The reactivity of the IF(n) (n=3,5,7) compounds toward lewis acids and bases were rationalised using molecular orbital analysis and their stability and methods of preparing were predicted by analysing the relative total energy. The limitations in the technique were highlighted and discussed.
As the use of this technique is at the cutting edge, there are still many other limitations in the approach that are not realised. But with research, the limitations can be minimised(improved knowledge of basis sets) resulting in a more complete and very powerful tool in chemistry.
References
- ↑ M. R. Hartman, J. J. Rush, T. J. Udovic, R. C. Bowman Jr and S. J. Hwang J. Solid State. Chem., 2007, 180, 1298 - 1305 DOI:10.1016/j.jssc.2007.01.031
- ↑ M.S. Schuurman, W.D. Allen, H.F. Schaefer III, J. Comput. Chem., 2005, 26, 1106: DOI:10.1002/jcc.20238
- ↑ J. Glaser, Acta Chem. Scand. A, 1979, 33, 789
- ↑ D. J. Darensbourg, Inorg. Chem., 1979, 18, 14 - 17 DOI:10.1021/ic50191a003
- ↑ G. Hogarth, T. Norman, Inorganica Chemica Acta 254 (1997) 167 - 171.
- ↑ 6.0 6.1 6.2 F. A. Cotton, Inorg. Chem., 1963, 3, 702 - 711 DOI:10.1021/ic50015a024
- ↑ Shriver and Atkins, Inorganic Chemistry, 4th edition, 2006, Oxford University Press, 408-409
- ↑ Housecroft and Sharpe, Inorganic Chemistry, 2nd edition, 2005, Prentice Hall, 479-480
- ↑ Housecroft and Sharpe, Inorganic Chemistry, 2nd edition, 2005, Prentice Hall, 479-480