Rep:Mod:sgk1916
Module 2: Bonding (Ab initio and density functional molecular orbital)
Tutorial
In the tutorial section, an optimisation of BH3 was performed. The following properties were recorded:
1. Optimised H-B bond distance = 1.19A 2. Optimised H-B-H bond angle = 120°
From the summary, the following properties were recorded:
| File Type | .log | |
|---|---|---|
| Calculation Type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | 3-21G | |
| Final Energy (a.u.) | -26.46 | |
| Dipole Moment (Debye) | 0.00 | |
| Point Group | D3H | |
| Calculation Time (s) | 10.0 |
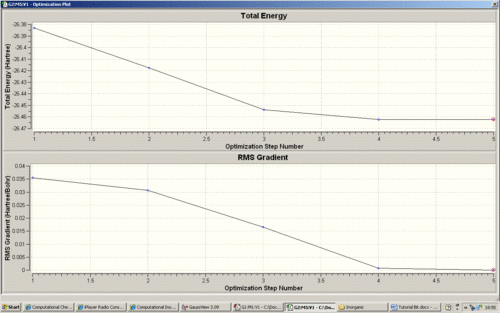
Furthermoer the intermediate geometries were observed and the first graph below visualises the steps in which Gaussian attempts to reach the energy minimum by altering the structural orientation. The second graph is the first derivative, which is used by Gaussian to 'find' the energy minimum of the PES by using the point where the gradient is zero.
Similarly an optimisation for B3 was performed, under the LANL2MB basis set. The use of the more advanced basis set reflects the increased lenghth of calculation.
1. Optimised B-Cl bond distance= 1.87A 2. Optimised Cl-B-Cl angle = 120°
| File Type | .log | |
|---|---|---|
| Calculation Type | FOPT | |
| Calculation Method | RB3LYP | |
| Basis Set | LANL2MB | |
| Final Energy (a.u.) | -69.44 | |
| Dipole Moment (Debye) | 0.00 | |
| Point Group | D3H | |
| Calculation Time (s) | 13.0 |
These examples enables one to understand the approach of computational chemistry and lays down the foundations of what in fact can be achieved from it.
Independant Work
To gain further knowledge of Gaussian, PCl3, was selected to optimise and it's properties to be reported.
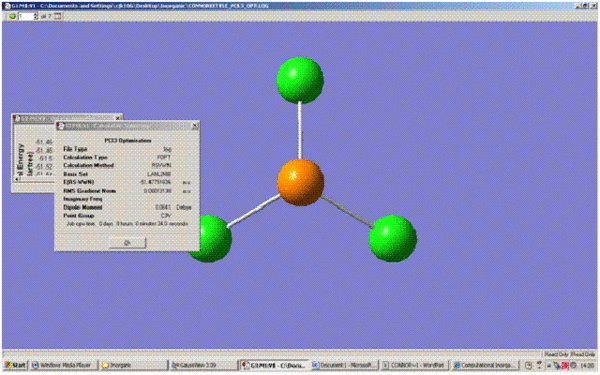
| File Type | .log | |
|---|---|---|
| Calculation Type | FOPT | |
| Calculation Method | RSVWN | |
| Basis Set | lanl2mb | |
| Final Energy (a.u.) | -51.48 | |
| Dipole Moment (Debye) | 0.0641 | |
| Point Group | C3V | |
| Calculation Time (s) | 34.0 |
P-Cl Bond Distance = 2.09
Cl-P-Cl angle = 109.47°
Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z
1 15 0 0.000000 0.000000 0.000000 2 17 0 0.000000 0.000000 2.090000 3 17 0 1.970471 0.000000 -0.696667 4 17 0 -0.985235 -1.706478 -0.696667
As can be seen the basis-set was altered froma 3-21G to LANL2MB. ASa result more information was available but the calculation was more intense and longer. This is the key balance that must be addressed when dealing with computational chemistry.
Vibrational Analysis
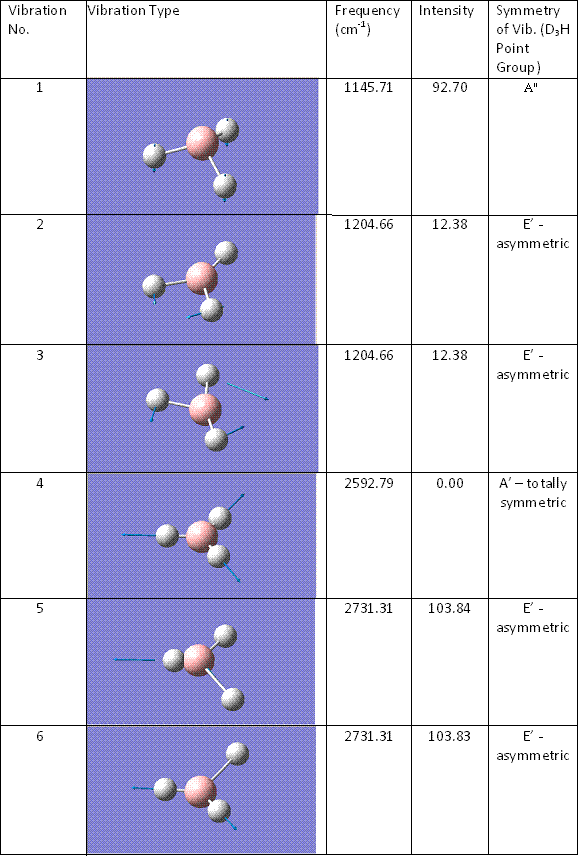
A key component in the computtional study of inorganic compounds is the ability to produce an IR spectrum and to animate the vibrations that arise from it. The vibrations of BH3 were animated in GaussView and tabulated here.
Below is the IR spectrum of the BH3 vibrations.
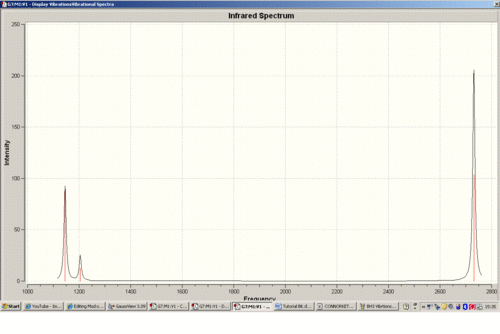
There are six tabulated vibrations however there are only three peaks observed on the IR spectrum. This is because the two vibrations at 1204cm-1 are degenrate and so are integrated into one larger peak. The vibration at 2592.79cm-1 is totally symmetric. There is no change in dipole moment of symmetry and therefore it is not IR active i.e. it does not show as a peak. FInally the two virations at 2731.31cm-1 are the same assymetric vibrations but upon different hydrogens. Therefore they are degenerate vibrational levels and again are integrated into one larger peak.
Molecular Orbitals
The valence Molecular Orbitals of BH3 were calculated using Gaussian. Of course, the calculated MO's from Gausian or delocalised i.e. spread over the molecule. As a comparison the Molecular Orbital diagram of BH3 was produced in terms of atomic orbital contributions. See below:

Key points that arise from the MO diagram:
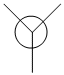
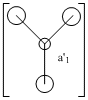
1. In the a'1 MO, there is a larger contribution from the H3 fragmentorbial as it is in closer in energy as compared to the a'1 atomic orbital from Boron. This idea of greater contribution is evident throughout all MO's.
2. In-phase overlap results in bonding orbitals, out-of-phase overlap results in anti-bonding orbitals. As a result, anti-bonding orbitals are more destabilised than bonding orbitals are stabilised.
3. The e' fragment orbitals are of higher energy and will combine with the e' A.O's from Boron, and so the splitting will be relatively larger due to interactions lying directly between bonded atoms.
4. A.O's can only combine if they have the same symmetry. As the pz orbital from Boron has a unique symmetry, a2, it will not combine with any H3 fragment orbital. As a result it becomes a non-bonding MO with the same energy.
5. s-s orbital interactions are stronger than s-p interactions and so result in greater bonding/anti-bonding splitting.
6. Counter-balancing this though is the fact that e' A.O's are of greater energy than a'1 A.O's. See the two highest anti-bonding molecular orbitals for a case in point.
Below are the calculated MO's with their predicted qualitative equivalent
Calculated MO's




Predicted Qualitative MO's
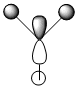
The first MO is clearly a non-bonding orbital. It consists of the Boron 1s orbital only as it is not a valence orbital and so is not high enough energy to combine with a H3 fragment orbital. As a result it is not included in the molecular orbital diagram.
There is a large correlation between the two methods of molecular analysis. As can be seen, the phases of the orbitals are in similar areas and both deal with the absence of a H 1s orbital in one of the degenrate e' fragment orbitals in that the quantitive method does not spread the MO to this area of the molecule.
It shows the the qualitative method is reasonably accurate and is excellent if a rough idea of molecular orbitals is required and computational chemistry is not available. However there are limitations. For more complex molecules, with more atoms and contributing atomic orbitals, the resultant molecular orbitals via the quantitative method become more delocalised over the course of the molecule and so are less obviously similar to the more phase defined molecular orbitals from the predicted qualitative method.
Isomers of Mo(CO)4L2
transMoguy |
cisMoguy |
Gaussian was used to investgate the difference in geometric properties of cis and trans octahedral isomers. It also lays claim to the dilema that a computational chemist may face when one is undertaking such analysis; attaing the balance between computational cost and power and amount of valuable information. This was experienced as optimations were run for both isomers with a reduced basis set, LANL2MB and a more advanced basis set/pseudo-potential, LANL2-DZ.
| Basis Set | Mo-P(1) Bond Length (A) | Mo-P(2) Bond Length (A) | Mo-P(1)-C Bond Angle(°) | Mo-P(2)-C Bond Angle(°) | P-Mo-P Bond Angle(°) | |
|---|---|---|---|---|---|---|
| LANL2MB | 2.74 | 2.75 | 125.7 | 119.4 | 93.1 | |
| LANL2DZ | 2.65 | 2.65 | 123.3 | 118.3 | 95.3 |
Labelling of P atoms
| Basis Set | Mo-P(1) Bond Length (A) | Mo-P(2) Bond Length (A) | Mo-P(1)-C Bond Angle(°) | Mo-P(2)-C Bond Angle(°) | P-Mo-P Bond Angle(°) | |
|---|---|---|---|---|---|---|
| LANL2MB | 2.65 | 2.65 | 116.6 | 117.8 | 180.0 | |
| LANL2DZ | 2.57 | 2.57 | 115.7 | 117.1 | 180.0 |
Labelling of P atoms
The tabulated values reveal how results can alter markedly when the basis set and/or pseudo-potential is changed. In particular are the cis-P-Mo-P angle. For a normal octahedral complex the optimum bond angle between cis groups is 90°. However to accomodate with the large PR3 groups which end up next to each other, and to limit steric hinderance, the bond angle is increased slightly. Both sets allow for this as they both have angles over 90°, yet the values differ; this typifies how a difference in basis set can cause a large difference in geometric properties. This can be put down to the fact that the second basis set, LANL2DZ, takes greater consideration of the core electrons, and hence is a better pseudo-potential. As a result the bond angle is greater as the basis set considers such electrons which have an inherent affect upon the orientation of the ligand. The greater bond angle was already observed with the lower basis set, and so a higher one will maximise this affect, due to the possible added repulsion of the core electrons in both PMe3 groups. Literature states that the P-Mo-P bond angle is 94.8° for PPhMe2 ligands. There is relative accuracy, however the reason the expected larger difference, due to the addition of the sterically demanding Ph group, is not observed, is because of the ability of the R groups to rotate around the P atom to an orientation wherein the less sterically demanding Me group is closer to the cis-PR3 ligand.1 Analysis of literature values reveal that the Mo-P bond length from x-ray crystallography is in fact 2.529 A. However this value is for PMe2 ligand and so is not valid to compare fundamentally. It seems though that as as the methyl groups are replaced with phenyl groups, that the bond length increases by around 0.022 A each time. This is due to the fact that as more sterically demanding groups are attatched, there a greater bond length is needed to prevent steric clashes between the R groups of the two P atoms. In fact, there seems to be correlation between the trans Mo-P bond length and the literature cis Mo-P value. This clearly tell us that the computational method is not entirely accurate. But it does correlate with the fact that sterically demanding ligands have a longer bond length when arranged in the cis fashion as compared to trans. This pattern is shown with the literature values of W-P bond lengths in the cis and trans forms, as detailed in this literature 2.
Frequencies

IR Spectrum of cis-Mo(CO)4(PMe3)2
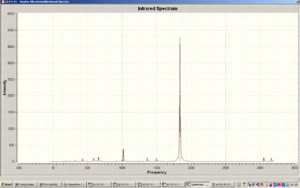
IR Spectrum of trans-Mo(CO)4(PMe3)2
By analysing the vibrational frequencies of a molecule displaying cis trans isomerism we can understand the steric and electronic effects of the two PR3 ligands. As there are almost one hundred frequencies of varying intensity, of particular importance are the CO stretches as they are the only ones that relate to that group and the symmetry of which are affected by the orientation of the remaining PR3 ligands.
For the cis complex, it can be said of the 4 CO groups that two are related trans and two are related cis. The stretches then are identical for the two trans and the two cis (as the trans couple has a PR3 cis to them, and the cis couple has a PR3 trans to them). As there are symmetrical and anti-symmetrical stretches related to both couples, there are 4 individual 4 CO stretches overall. Similarly for the trans complex, the 4 CO groups are all symmetrically related, in that all have a PR3 group cis to them. As a result the symmetrical stretch is not IR active as there is no change in symmetry or dipole moment. Therefore there is only one expected IR active CO stretch.
This theory is observed in both complexes.
Cis complex ν(CO)cm<up>-1: 1848.47(s), 1850.75(s), 1869.96(m), 1960.47(w)
The 1848.47 stretch relates to the assymmetric stretch of the two CO's cis to each other. The 1850.57 stretch relates to the assymmetric stretch of the two CO's trans to each other. The 1869.96 stretch relates to the assymmetric stretch of all 4 CO ligands. The 1960.47 stretch relates to the symmetric stretch of all 4 CO ligands.
Trans complex ν(CO)cm<up>-1: 1839.3
This degenerate frequency relates to the assymetric stretching of two trans CO ligands. The degeneracy results from the fact that there are two stretches as there are two groups of trans CO ligands. There are two further stretches recorded but they relate to the assymetric and symmetric stretching of all four CO groups simultaneously. As all four are seen as equivalent adn related by symmetry, these stretches are not IR active, as they 'cancel' each other and there is no change in overall dipole moment or symmetry.
Although no literature values could be found for the exact complexes, literature was found wherein the CO stretches of cis and trans Mo(CO)4L2 omplexes were displayed. The literature also showed that the cis-complex has four CO stretches, and the trans-complex has one CO stretch, correlating with the above assignments. They are in the same wavenumber region 1800-1950cm-1, but the difference in exact values came from the fact the central metal was tungsten, a heavier metal, and the PR3 was different, both of which alter value of the CO stretch. 3
The psuedo symmetry of the cis-isomer is C2v The pseudo symmetry of the trans-isomer is Ci Both are consistent with the IR frequencies and the behind them as above.
The difference in energies of the isomers is 2.93E-03 a.u. The more stable isomer is the cis isomer with a total energy of -773.36 a.u.
Advanced
As phosphorous prefers to utilise its low-lying d-orbitals and extend it's co-ordination, a greater basis set is needed which adds the d-orbitals to the the pseudo-potential of core electrons.
| Basis Set | Mo-P(1) Bond Length (A) | Mo-P(2) Bond Length (A) | Mo-P(1)-C Bond Angle(°) | Mo-P(2)-C Bond Angle(°) | P-Mo-P Bond Angle(°) | |
|---|---|---|---|---|---|---|
| LANL2MB | 2.55 | 2.55 | 116.6 | 116.8 | 180.0 |
| Basis Set | Mo-P(1) Bond Length (A) | Mo-P(2) Bond Length (A) | Mo-P(1)-C Bond Angle(°) | Mo-P(2)-C Bond Angle(°) | P-Mo-P Bond Angle(°) | |
|---|---|---|---|---|---|---|
| LANL2MB | 2.62 | 2.63 | 116.6 | 124.4 | 95.1 |
As can be seen, when the low-lying - orbitals are taken in to consideration, then there is adecrease in cis-Mo-P bond distance. In fact it falls within the 2.50-2.60 A ballpark for Mo-P bond distance, where increase is due to increased steric demand of the R groups on the PR3 ligand. This could perhaps be due to the back bonding from a lone pair on the Mo into the empty d-orbitals of the P, therefore increasing the bond order and strength, reducing the bond length. This possible through space interaction will ahve to be clarified through MO caluculations but it seems a logical hypothesis given the fact that the Mo-P bond length seemed shorter and more in tune with lit. values when the empty d-orbitals were taken into consideration in the pseudo-potential.
References
1. F. A Cotton, D J. Darensbourg, S Klein, W. S. Kolthammer, "Steric contributions to the solid-state structures of bis(phosphine) derivatives of molybdenum carbonyl. X-ray structural studies of cis-Mo(CO)4[PPh3-nMen]2 (n = 0, 1, 2)", Inorg. Chem., 21, (1982), p294-299
2. L. Hirsivaara, M. Haukka, J. Pursiainen, "Intramolecular hydrogen bonding and cation &pi-interactions affecting cis to trans isomerization in tungsten hexacarbonyl derivatives of 2-pyridyldiphenylphosphane and triphenylphosphane", Inorg. Chem. Comm., 3 (2000) p508-510
3. L. F. Dahl, D. L. Wampler, The Crystal Structure of Ruthenium Tetracarbonyldiiodide, Acta Cryst. (1962). 15, 946
Ammonia
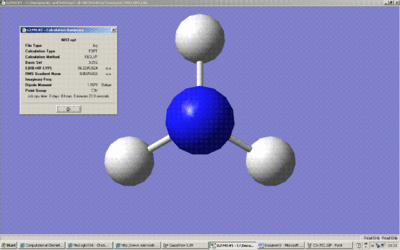
Above is the summary of the optimisation of NH3. The point group is C3v.
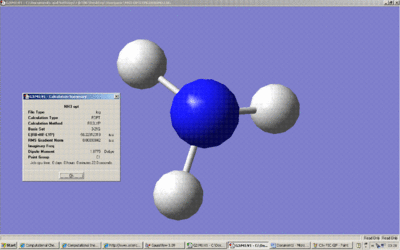
Above is the summary of the optimisation of an NH3 with one N-H bond extended to 1.01A . The point group is C1.

Above is the summary of the optimisation of the planar NH3 inversion transition state. The point group is D3h.
The symmetries of all three molecules resulted in differences in the optimised structures of each, for example when the inversion transition state was optimised, it resulted in a planar structure. However when one N-H bond was shortened, the optimised structure reduced back to the optimised 1.022A, yet the point group remained C1.
The time taken to optimise did increase with a deviation from the 'normal' NH3 structure, perhaps because the differing starting structure was not something Gaussian was used to in that it could not simply revert back to the pyrmidal NH3. The C1 point group (planar NH3) took the longest with 1 min 27 s.
Symmetry affects the calculation time in that if a molecule is not a specifically symmetric point group, e.g. C3v, but a specifically less symmetric group, e.g. C1, then more the more difficult elements of the point group will need to be defined, taking longer time. Conversely if the point group is not specific but symmetric, e.g. D3h, then there are many more elements that need to be considered that are not necessarily difficult. The sheer volume of elements as compared to C3v for example, increases the calculation time, as shown above. This is because C3v is a sub-group of the less specific D3h.
A molecule can break symmetry during optimisation as the interface moves the atoms involved to different orientations to gain the most energetically stable structure that relates to the starting structure.
If the starting structure is highly symmetric then it seems that the calculation time is longer, with analysis of the calculation time of the D3h NH3. This is perhaps due to the fact that the high symmetry needs to be broken for optimisation to occur, taking much longer, as well as the fact that there are more elements that need to be analysed for the final optimised structure.
The geometry with the lowest energy is the final one of the screenshots above i.e. the one with D3h point group.
The C1 isomer is 794.00 kJ/mol higher than the lowest energy geometry and the C3v isomer is 793.99kJ/mol higher than the lowest energy geometry.
The MP2 method
The method of optimisation was increased to the more effient MP2 method and 6-311+G(d,p) basis set to analyse what affect the difference would have on geometry, energy and in a practical sense time.
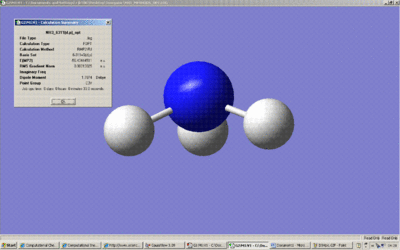
Screenshot of Summary (C3v)

Screenshot of Summary (D3h transition state)
Both optimisations took longer than the previous method and basis set optimisations. And again the D3h took longer to calculate for the same reasons as above. Obviously the more effiecent and accurate basis set on display here takes longer, as it takes more considerations of the structure into account.
The barrier height energy for the inversion of NH3 via the D3h transition state is 20.46 kJ/mol from ΔE=E(D3h)-E(C3v)
The barrier height (ΔE) has changed dramatically between the two methods, in fact it has decreased by an order of magnitude. This shows the greater accuracy of the MP2 method/6-311+G(d,p) basis set. It seems that the previous method would not be beneficial in the computational analysis of large complex molecules as, when converted into kJ/mol, the energy differnces for NH3 alone are far to inaccurate. Furthermore the previous method had the D3h inversion transition state as the lowest energy geometry, a point which due to the repulsive affect of the nitrogen lone pair is just not feasable, considering also that this geometry is the unstable transition state in the inversion mechanism
Compared to the experimental value of 24.3 kJ/mol, the computational value is quite accurate and allows the computational chemist to understand a reasonable estimate into how or whether the inversion mechanism proceeds. It also shows the importance of using an advanced method and/or basis set when it is possible.
Vibrational Analysis
Below is the IR spectrum of the C3v NH3 molecule

Below is the IR spectrum of the D3h NH3 molecule
There are five positive frequencies for the D3h molecule and six positive frequencies for the C3v molecule.
The vibrational modes in each molecule have the same motions, although not at the same wavelengths or order. The following pairs have the same character of motion:
| D3h | C3v | |
|---|---|---|
| -318.05 | 779.857 | |
| 1640.59 (1st vib) | 1746.89 (2nd vib) | |
| 1640.59 (2nd vib) | 1746.89 (1st vib) | |
| 3635.71 | 3384.54 | |
| 3854.27 (1st vib.) | 3536.01 (1st vib.) | |
| 3854.27 (2nd vib.) | 3536.01 (2nd vib.) |
Howard displays the experimental frequencies as follows ν(NH3)cm-1): 950, 1631, 3355, 3470
There is some correlation here. Howard states that computationally, the first peak will inaccurate because the vibration includes an anharmonic term and is not at infinitesimal amplitude. The final two peaks are small in comparison to the others as the vibrations are near symmetric so therefore less change in dipole moment and therefore lower intensity. Howard also speculates that there is a overtone-combination band, i.e. the combination of two previous bands to form an 'overtone'. Therefore I speculate that there is an overtone at 5131.43cm-1 i.e ν2+ν3=1746.89+3384.54 or 5282.9cm-1 i.e. ν2+ν4=1746.89+3536.01. Determination of which wavenumber the overtone would be could arise from the fact that the former combination results in a perpindicular-type band while the latter results in a band with perpendicular and parallel components.1
The value of the D3h negative frequency is -381.05cm-1. The reason for this negative frequency is to do with the 2nd derivative of the PES. Normally when there is an energy minimum the 2nd derivative is postive and this relates to a vibration with a positive frequency. However in this instance, vibration is an energy maximum, therefore the 2nd derivative is negative which relates to a negative frequency. The fact that this vibration is an energy maximum, realtes to the structure of the molecule, in that it is a transition state (as a transition state is a oeak in energy).
The first vibration follows the inversion mechanism, as it is the symmetric inversion of the orientation of the hydrogens.
Literature
1. J.B. Howard, On the Normal Vibration Frequencies of NH3, PH3 and AsH3, Journ. Chem. Phys., 3, 207, 1935 2. P. Schwerdtfeger, P.D.W. Boyd, T. Fischer, P.A. Hunt, and M. Liddell. Trends in Inversion Barriers of Group 15 Compounds. II. Ab-initio and Density Functional Calculations on Group 15 Fluorides." J. Amer. Chem. Soc. , 1994, 116, 9620
Mini Project- Computational analysis of Fischer Carbenes and Schrock Alkylidenes
In this project I aim to investigate the geometry, frequencies and electronic nature of specifically the Fischer carbene, with close reference to the Schrock analogue. This results in an analysis of the type of bonding evident in such carbenes and the electronic state of the carbene carbon
WIth reference to slides 3 and 4 of Dr. Ed Marshall's Advanced Organometallic course 1, it is undertood that there are two types of metal-carbon double bonds; one which follows the Fischer model(=CXR) and one which follows the Schrock model(=CHR). Initially it was found that the when one of the carbonyls in the hexa-carbonyl tungsten complex was replaced with a carbene group, the molecule can follow either of the model, dependant on the carbene substituents. With research it was found that for the Fischer model to be favoured, X=OMe and R=Ph and that similarly the Schrock model is favoured when X=H and R=Ph. Both models prefer their respective R groups to be relatively large alkyl or aryl groups and in the interest of keeping certain parameters the same to allow for fair comparison, both were kept the same. However, and this is where one of the limits of computational chemistry raises it's head, Gaussian finds it difficult to work effieciently with bulky groups such as tert-butyl, which would have been more favourable for the Schrock model, and so a compromise of R=phenyl ring was settled upon.
Proposed Fischer carbene: Mo(CO)5(CPh(OR))
Proposed Schrock Aklylidene: Mo(CO)5(CHPh)
Firstly a pre-optimisation had to be run as the relatively large molecules in question would be perhaps too much for Gaussian to optimise at a high level basis set in one go. Therefore the LAN2MB basis set (method: DFT) was chosen. Furthermore two optimisations had to be run for both models; one in which the carbene carbon is in the singlet state and one in which it is in the triplet. This essentially forms the basis for the investigation as it is these properties that effect the subtle difference in bonding between the two. The multiplicity with the lowest energy will be taken as the one which is the actual case for bonding in each model. From the preliminary pre-opts, they were re-run (both triplet and singlet) at the higher basis set LANZDZ, which obviously took a longer calculation time on the 'scan' service. It was found that the singlet form of the Fischer carbene was the more stable.
| Multiplicity | W-Carbene Bond Length (A) | CO-W-Carbene Bond Angle(°) | Total Energy (a.u.) | |
|---|---|---|---|---|
| Singlet | 2.16 | 178.44 | -1019.28 | |
| Triplet | 2.23 | 159.30 | -1019.21 |
fischer singlet |
Singlet Fischer model
fischer triplet |
Triplet Fischer model
As can be seen the singlet state is the more energetically stable multiplicity, relating to a -181.61 kJ/mol energy difference between the two. Pivotally we can also speculate that the triplet state is less stable from the larger deviation from the optimum 180° CO-W-Carbene bond angle. It would be expected to be not as great as this considering the the longer bond length which alleviates some of the steric strain of the carbene group. However the angle itself would almost be enough to realise that the singlet state is the most stable
| Multiplicity | W-C Bond Length (A) | CO-W-C Bond Angle(°) | Total Energy (a.u.) | |
|---|---|---|---|---|
| Singlet | 2.12 | 176.78 | -904.77 | |
| Triplet | 2.21 | 152.50 | -904.70 |
schrocksinglet! |
Singlet Schrock model
schrocktriplet |
Triplet Schrock Model
In the Schrock alkylidene however, a problem arises. It was speculated that the Schrock alkylidene, with its non pi-donor substiuents on the 'carbene' analogue, prefers the triplet multiplicity. However is evident that the singlet is the most stable multiplicity, by some 145.89 kJ/mol. This proceeded to cause a unanswerable anomaly, but with research, it was found why this was the case. A Schrock alkylidene would not be able to prosper under such conditions as the ones in which the optimisations were run. For example, although the non-pi donor nature of the alkylidene substiuents were correct, it was the central metal and particularly the co-ligands that prevented the triplet multiplicity being more stable. CO ligands are pi-acceptor ligands, and although they work well in the Fischer model (see later), for the Schrock model, they are not useful. This is because there are a pi bond is formed via the single electron donation from the C sp2 orbital and the similarly for the p orbital. A pi-acceptor co-ligand wold render this type of bondng pointless as the electron density, which I speculate would be less than the 2 lone pair bonding observed in the Fischer model, would be lost. Similarly the central metal atom, despite displaying the Schrock model in certain circumstances, is not the optimum high-oxidation metal for the model (Ti, Ta are more recognised). The conditions for tungsten related Schrock alkylidenes contains a mono-substituted C group wih a tert butyl as well other sterically demanding co-ligands, which through experience of this lab, would be too much for Gaussian to provide reliable, efficient results.1.
These circumstances contributed to the fact that the complex in question simply does not exhibit the Schrock model, but does exhibit the Fischer model. Geometric and energetic analysis cntributed to this research which allows one to realise the further conditions required to allow for each model, e.g. the donor/acceptor ability of co-ligands, the oxidation state of the metal centre, steric bulk, C-substituents. As a result it was deemed irrelevant to continue the analysis of the supposed Schrock model; however the analysis up to this point did prove vital in determining the set conditions fro such a model to be observed.
Fischer carbenes require pi-donor substiuents upon the carbene. This is to increase pi-electron density upon the carbon , which then is donated onto the metal centre. Schrock alkylidenes however require non-pi donor substituents as they donate two lone electrons via different orbitals, hence the triplet multiplicity. Increasing the pi density at the carbon would prevent this from occuring readily and may alter the model to the Fischer model.
Frequencies
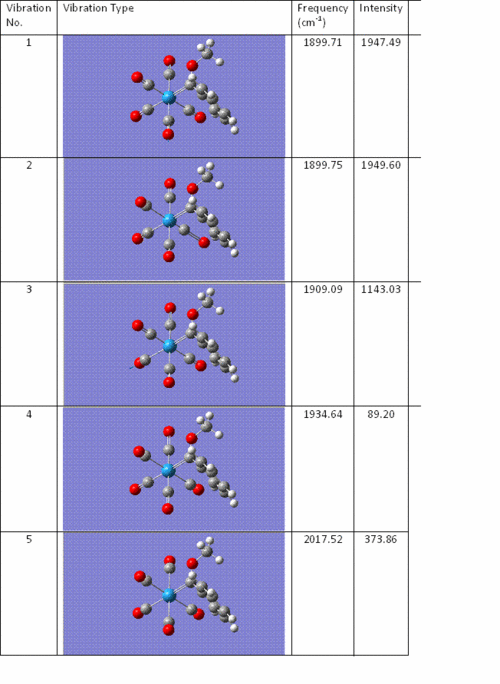
Below are the frequencies of the key CO vibrations in the Fischer carbene, Mo(CO)5(CPh(OR))
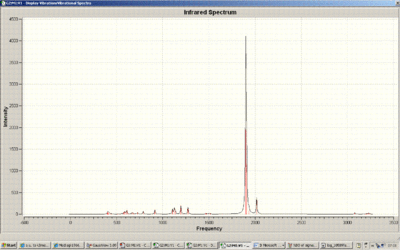
Below is the IR spectrum of Mo(CO)5(CPh(OR)). Note the dominance of the CO vibrations in the spectrum.
MO analysis
Of particular importance in the Fischer model is the orbital interactions between the metal centre and the carbene carbon. Therefore a full quantitative molecular orbital analysis was run to identify possible through space interactions, which may strengthen the case for the model. This was incorporated into the frequecy calculation by adding 'pop=(full,NBO)' into the keywords (method: DFT, basis set: LANZDZ)
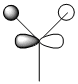
It is known that the Fischer model exhibits what is effectively, two types of bonding; σ donation of electrons from the sp2 hybrid orbital into and empty p-orbital on the metal centre and π back-bonding of electrons from the metal centre d-orbital to the empty p-orbital on the carbene carbon. The σ donation occurs because, the carbon multiplicity is singlet and therefore there is a lone pair of electrons in the same orbital. See below for a schematic diagram.2 Conversely when this pair of orbitals are no in the same orbital triplet multilpicity arise which is observed in Schrock chemistry.
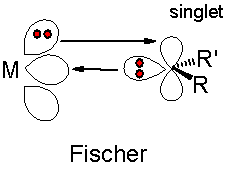
A powerful tool of computational chemistry is to see whether such orbitals actually exist via a molecular orbital calaculation. This proves all the more valid because the bonding described is in terms of localised atomic orbitals, something which is a theory based simplification. Therefore the MO calculation allows the chemist to speculate whether such through-space interactions can occur in terms of the more quantitative oomputational molecular orbital theory.

This screenshot shows a possible orbital for σ accpetance from the sp2 orbital of the carbene. It is an unoccupied orbital, no. 76.
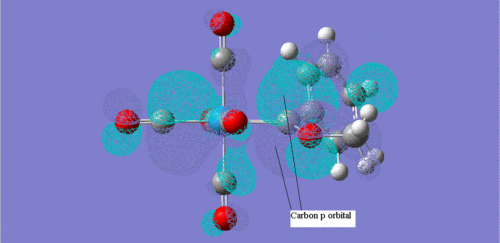
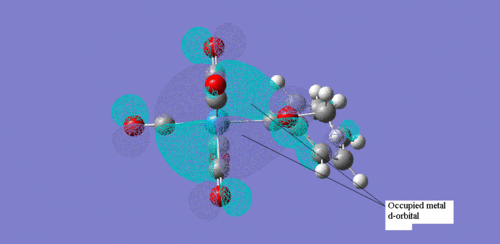
These two screenshots are of the 75 and 73 molecular orbitals respectively. These MO's reveal the real life orbitals of the simplified Fischer model. It must be remembered though that the atomic orbitals were considered in the model are not dynamic representations of the overall MO's but in fact contribute to the overall nature of the MO. For instance we can see in the MO 73 which is occupied, there is a component that is a d orbital of the metal centre. Similarly, in MO 75, which is unoccupied, there is a component on the carbene carbon which represents the empty p-orbital. Therefore we can justify then that there is some through space interaction or donation from the occupied metal d-orbital component of MO 73 through to the empty p-orbital of the carbon carbene of the unoccupied MO 75. They are of the correct orientation and phase correlation for a donation to proceed.
Analysis of the MO's allows the computational chemist to ascertain whether in this case, certain interaction/donations may occur based upon the arrangement of the MO's. But to ascertain the actual bonding nature evident in a molecule, then the Natural Bond Order must be analysed. This was gained via the frequency calculation (adding 'pop=(full,nbo)' to keywords) and is viewed as a .log file.
Pivotally, though we can see that thereis a donation between the metal d-orbital nd the empty p orbital on the carbene carbon

It can be seen that the 6th natural bond is between tungsten (W) and C(6) which relates to the carbene carbon from earlier reading of the file. It states that the 2 centre bond (BD) has an order of two. Furthermore and critically, it states that the bonding interaction of the tungsten comes 99.02% from a d-orbital and of C(6) 99.99% comes from the p-orbital. Interestingly wecan see that 79% of the NBO still rests upon the tungsten 'hybrid', in part due to the greater polarisation co-efficient cA of tungsten, which alone suggests there must be other donations at play to allow a full stable bond. This evidence ties in with the fact that there is d-p backbonding which results in a π bond, all of which is described in the NBO analysis.
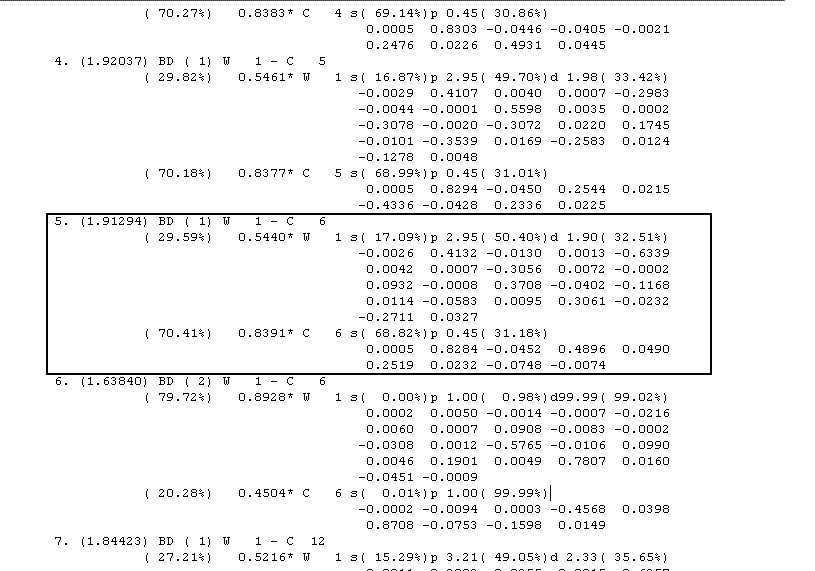
The σ bond element is also described in the NBO analysis. The 5th natural bond, between W and C(6), reveals the extent of this. It states it is a 2centre bond (BD) but this time there is only a single bond order, consistent with the σ nature. The bonding is between a C hybrid with an unusual 68% s character and 32% p character, and a tungsten hybrid consisting with varying s, p and d orital character. Again the NBO rests primarily upon the donor (carbon) as shown by the percentage (cA-squared) but so this balances out over the two binding types as the same occurs above. The fact that there is no defined orbital for the tungsten acceptor leads one to believe that the donation does not occur into an empty p orbital as previously thought, but a hybrid of s,p and d orbitals, something that correlates with the shape of the assigned tungsten acceptor orbital above (1st MO screenshot). Finally the σ nature of this NBO is confirmed as the energy is 1.913 (units not supplied) compared the 1.638 of the d-p π backbonding NBO. This correlates with the idea evident throughout MO theory that single bonds are stronger than π bonds.
This mini-project was firstly an investigation in to the relative stabilities of Fischer and Schrock models of the tungsten hexa-carbonyl parent group. This would be achieved altering the C-substituents on the carbene/alkylidene ligand. However with private research away from the lecture notes from which the interest was sparked, it was realised along with analysis of optimum structures that a Schrock aklylidene was not present from the parent molecule. This is due to a variety of reasons as explaines from co-ligands to the heaviness metal centre. As a result primary focus was applied to the Fischer model wherein specifically, the MO's were analysed to explain possible bonding models and vitally NBO's were evaluated to gain fundamental evidence of the possible bonding model as hypothesised after MO analysis. IR spectra was also tabulated and close attention was applied to the CO bond vibrations.
Literature
1. Lecture Notes - http://webct.imperial.ac.uk/webct/cobaltMainFrame.dowebct
2. R. Schrock High-Oxidation-State Molybdenum and Tungsten Alkylidyne Complexes, Acc. Chem. Res., 19, 342-348, 1986
3. V8rik, wikipedia user, en:Image:Germanabenzene.png, 20/06/2006
4. NBO Analysis - http://www.chem.wisc.edu/~nbo5/tutorial.html