Third Year Computational Lab: Module 3

Experiment 3: The Transition State

The Cope Rearrangement Tutorial

In this section I shall be investigating the transition state in the well studied reaction, the cope rearrangement.

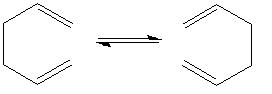
The reaction is generally believed to go via a concerted transition state in either the boat or the chair conformation;

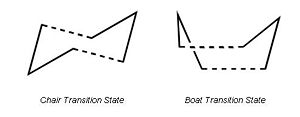
In this exercise the relative energies and symmetries of the two transition states will be investigated and the vibrational frequencies will be modelled computationally.

Optimising The Reactants and the Products

The starting material, 1,5-hexadiene was drawn in gaussview and optimised so that all the largest groups anti to each other. This was then optimised using Gaussian and a Hartree-Fock method and a basis set of 3-21G.

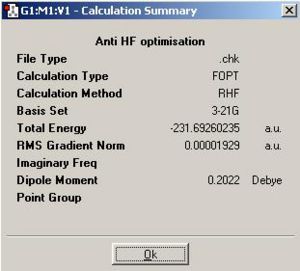
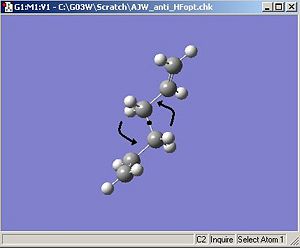
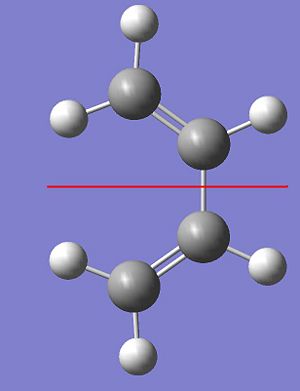
The optimised product was symmetrized and was found to have a point group of C2. The C2 symmetry operation is illustrated below. It is necessary to 'symmetrize' a product because although the program can optimise a geometry of a molecule with great precession, the bond angles produced and other important geometric parameters are subject to rounding errors. These errors are insignificant to almost any further use of the optimised product apart from the calculation of the symmetry which requires 'exact' answers. This is why the molecule must be adjusted according to it's approximate symmetry to give it a higher nsymmetry and how sometimes the search criteria must be relaxed to find the true level of symmetry in the molecule.

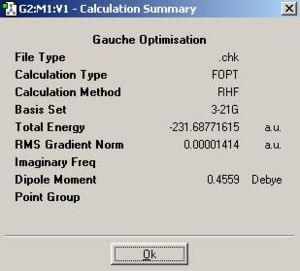
The same process was repeated but with the 4 central atoms lying gauche to each other. This is expected to be higher in energy as gauche conformations are almost always higher in energy due to 1,4 van der waals repulsions between the largest group as well as a reduced anomeric stabilisation.

The geometry of the gauche conformation pre-optimisation is shown below.

	a.u.	Kjmol-1
Anti Conformer	-231.6926024	-608308.9275
Gauche Conformer	-231.6877162	-608296.0988

As predicted the conformer with all the 4 central central carbons anti to each other is indeed lower in energy.

A Discussion of the Relative Energies of the Conformers

The energy of the conformation will depend on several factors including, the amount of steric strain present, the possibility of secondary orbital interactions (hyperconjugation), the possibly of stabilising dipole intramolecular dipole interactions (H-bonding) as well as more minor factors like the reduction in the resultant dipole in the molecule. In the molecule under discussion, the major factors will be the first two and both of these favour the formation of the anti conformers. Anti conformers allow their largest substitutents to be furthest away form each other and hence relieve 1,4 van der waal interactions as much as possible. A more minor factor that will affect the conformations is that hyper conjugation interactions between C-Cδ and C-Cδ* and this will stable the anti orbitals. I predict that the lowest energy conformation will be the anti2 conformation becuase it involves the all anti conformations and has the two large -CHCH2 pointing in opposite directions further minimising the steric strain.

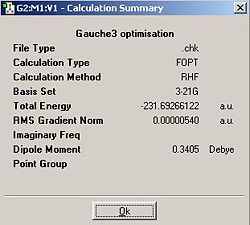
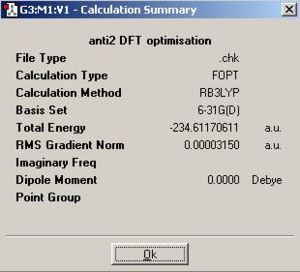
I tested to see whether this was the lowest energy conformation and found that, at this level of theory it isn't. Gauche3 (the optimisation summary shown below) was shown to be lower in energy when optimised at this level of theory. I struggled to rationalise this so I theorised that this was actually an error with the level of theory used. I reoptimised the Gauche 3 conformer at a B3LYP/6-31G* level of theory and found that the energy given by the conformer at this level of theory (-234.61132932a.u) is actually higher than the anti2 conformer (-234.61171 a.u.) at the equivalent level of theory. Consequentally I can say anti3 is likely to be the lowest energy conformer for the reasons already discussed but computationally this lowering in energy doesn't be come proniunced until a B3LYP/6-31G* level of theory is used.

first Jmol

The anti conformer initially optimised was the 'anti1' conformer named in the appendix. The energy, symmetry and geometry (as far as I can tell) are identical.

The Gauche conformer initally optimised is 'gauche1' conformer named in the appendix. The energy, symmetry and geometry (as far as I can tell) are identical.

Optimising the 'anti2' conformation

The conformation defined as anti2 in the appendix was built and optimised to yield the following calculation summary for optimisation.

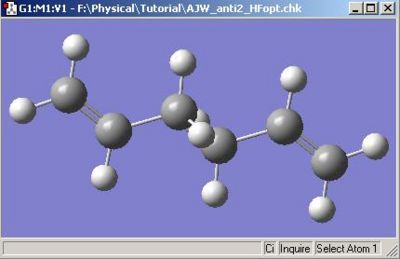
The energy, 231.61254 a.u. is the same to the energy quoted in the table as is the symmetry and the appearance of the molecule. Consequently I can say with some confidence that the correct conformation has been drawn. This structure was then optimised further with a DFT method at B3LYP/6-31G* level of theory.

Comparing Energies and Geometries of the anti2 conformer at different levels of theory

Pentahelicene

The energy of the HF optimised conformer, -231.61254 a.u., is significantly higher than the energy of the DFT optimised conformer,-234.61171 a.u.. However, there is not a huge noticeable difference between the geometries.

The angle between the bond between one of the sp2 carbons and one of the carbon atoms adjacent to the SP2 carbons and the bond between the two atoms adjacent to sp2 carbons is 112.66475° in the DFT optimised geometry and 111.35284°. And the bond between the two atoms that are adjacent to SP3 carbons (the bond that bridges the two planer sections of the molecule) is shorter in the DFT optimised geometry at 1.54808Å than in the HF optimised geometry which is 1.55284Å. The other bond length are even more similar, and the significant dihedral angle, between the 4 central carbons, is 180° for both as would be expected in the anti conformation.

In conclusion, the HF geometry was only subject to a very minor change in geometry upon optimisation when a DFT method was employed but that it produced a much lower energy isomer.

Investigating the Energies of the anti2 conformer and a comparison with the experimental values.

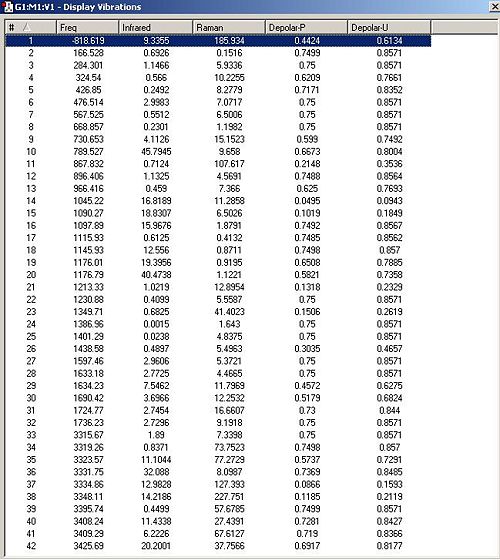
The conformer optimised at the B3LYP/6-31G* level was then used to produce a calculation of the vibrations in the molecule. This is to enable comparison with measurable attributes that can be calculated experimentally.

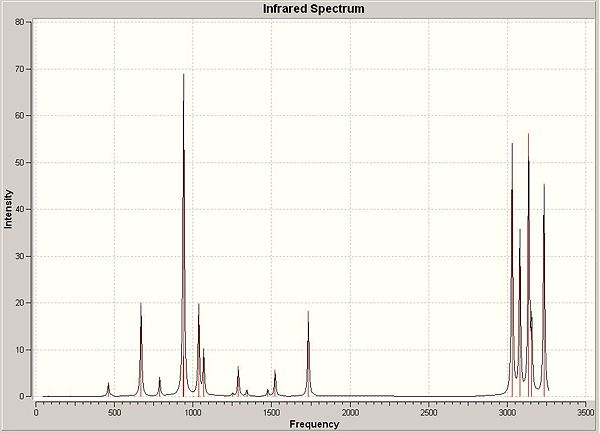
The vibrations calculated were checked to see if there were any 'imaginary' vibrations (vibrations with a negative frequency) that are only present if the molecule is a maximum (i.e. a transition state) rather than a stable conformation. The follwing energies terms were produced and compared with experimental values.

Sum of electronic and zero-point Energies

Sum of electronic and zero-point Energies= -234.469195 Hartree/Particle

This is defined as the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE). At this temperature there will be electronic energy as it does not depend on heat but no translational energy or rotational energy and only zero-point vibrational energy (because these energies are the expression of heat within the molecule which would not exist at absolute zero.

Sum of electronic and thermal Energies

Sum of electronic and thermal Energies= -234.461847 Hartree/Particle

This is the total internal energy as would be predicted at 298K and 1 atmosphere. It will be the sum of electronic, rotation, vibrational and translational.

Sum of electronic and thermal Enthalpies

Sum of electronic and thermal Enthalpies= -234.460903 Hartree/Particle

This will be the totally internal energy as before but with the adjustment for the thermal energy RT (H = E + RT).

Sum of electronic and thermal Free Energies

Sum of electronic and thermal Free Energies= -234.500782 Hartree/Particle

This finally value also includes an entropy term as G = H -TS.

Optimizing the "Chair" and "Boat" Transition Structures

The Optimisation of the Chair Transition State by Computing the Force Constants

In this section the transition state featured in the cope rearrangement drawn earlier.

The chair conformation transition state was constructed from two optimised CH2CHCH2 fragments that had been orientated into roughly the correct position for the chair transition state.

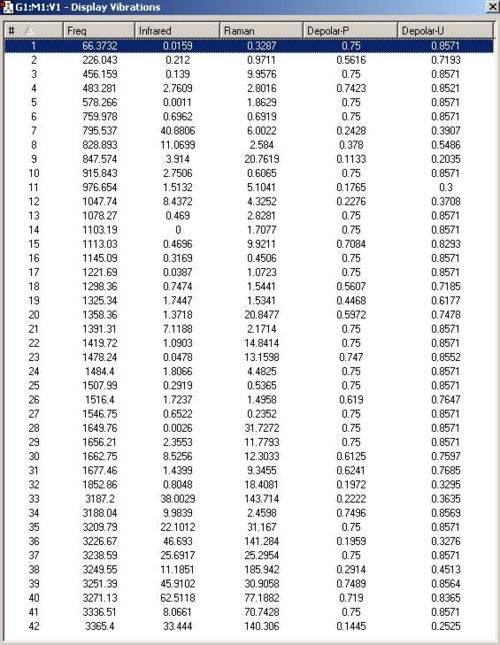
This was then optimised using a HF/3-21G level of theory to produce a predicted geometry and vibrational frequency table.

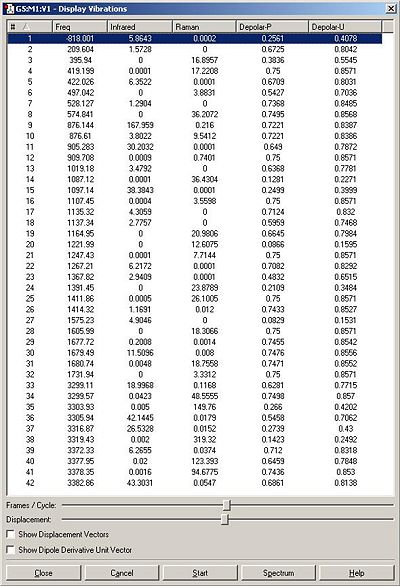
The imaginary vibration did indeed correspond to the correct transition state because when animated in involved the shortening and lengthening of the inter-atomic distance between the terminal carbons alternately, and this would correspond to the creation and breaking of bonds between the terminal carbons, first on one side, then on the other. As this is a very specific feature of the cope rearrangement It adds further credence to the belief that the transition state has been optimised correctly.

The Optimisation of the Chair Transition State Using the Redundant Coordinate Editor Method

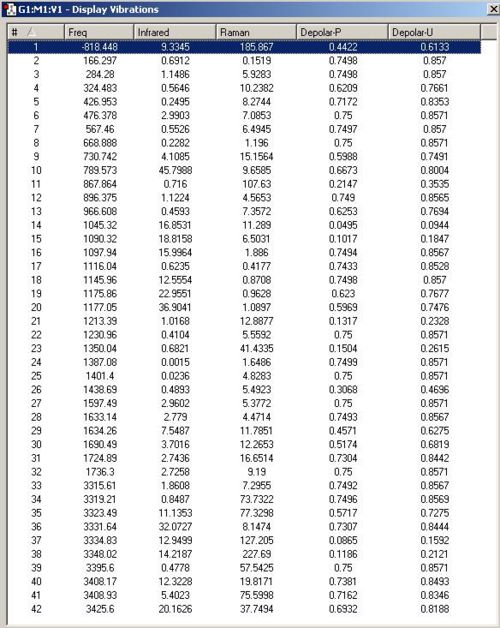
The initial guess used in the previous exercise was copied and pasted into a new molgroup in gaussview. This time the redundant coordinate editor was used to constrain the terminal carbons into a bond restricted to a bond length exactly 2.2Å; a frozen coordinate. This was then optimised to a HF/3-21G level of theory. The output from this optimisation was then optimised a further time with the restriction on the bond both removed. After this was completed, the predicted vibration frequencies were calculated to the same level of theory

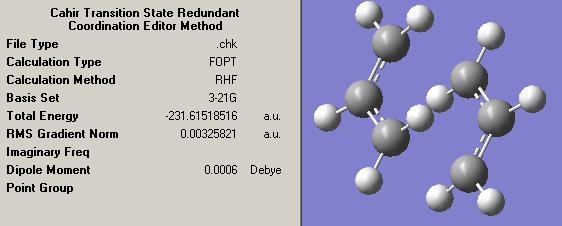
The transition state geometries calculated from the two outputs was compared.

Both methods gave very similar energies and geometries. The redundant coordinator method gave an energy of -231.6194203a.u. whereas the opt berny method gave an energy of -231.61932237 a.u. It is not unexpected that the frozen coordinate method gives a slightly lower energy because it is a slightly more sophisticated technique; by breaking down the optimisation into two steps it's less reliant on the 'guess' transition states accuracy and less likely to get stuck in an inappropriate local energy minima. The other significant aspect in which they differed was the interatomic distance between the terminal carbons that are in the proces of bond forming. The redundant coordinate method gave this length as 2.02041Å whereas the opt berny method gave this length as 2.02035Å.

Optimising the Boat Geometry using the QST2 method

In this method the computer attempts to interpolate a transition state from the initial state (the reactants) and the final state (the products). In theory the transition state should be the energy maximum between these two points.

The job was submitted to optimise to a TS (QST2) transition state, but it failed as the initially geometries are so far away from the transition state geometries that the calculation tried to perform the incorrect operation to convert one to the other.

The initial geometry was tweaked so that it was initially more boat-like. This was done by modifying the dihedral angle in the central 4 atoms in the reactants and the products to 0°. Also the angle between any 3 adjacent atoms within the central 4 atoms was set to 100°. The two modified geometries were resubmitted.

The QST2 Method output

The calculation returned a 50 different geometries along different stages in the reaction coordinate. Below I shall show pictures of the important points along the rearrangement.

The computed reaction geometry progression does not correspond well to what would have been predicted because as shown, it is not concerted. There is a bond broken well before the next bond is formed. This may be explained by the fact that the gaussview representation of bonding is rather arbitrary, it may not show a bond when the bond is merely very long. Apart from that the representation produced seems consistent to what would be predicted.

Unfortunately the system never reaches an absolute minimum energy state. This means that there are several options available. Firstly the final state produced can be reoptimised and the geometry should converge on the low energy geometry coresponding to the 'finished' in the process. I believe this would work because judging by the energy/reaction coordinate diagram the final state is very close to the lowest energy geometry and hence the optimisation, if run, is unlikely to fins some other local minimum. Secondly the entire QST2 IRC can be run again and a greater number of points can be specified. This is more computationally expensive but not beyond the capability accessible to me. The final option is to redo the IRC but specify in the calculation the the force constants must be computed after each step. The first and the second options were used, the final was deemed to take too much computer time to be convenient in this instance.

The first method yielded the the lowest energy isomer, gauche3 when optimised as expected.

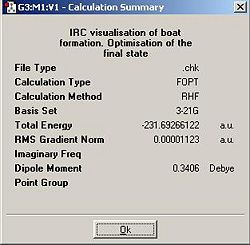
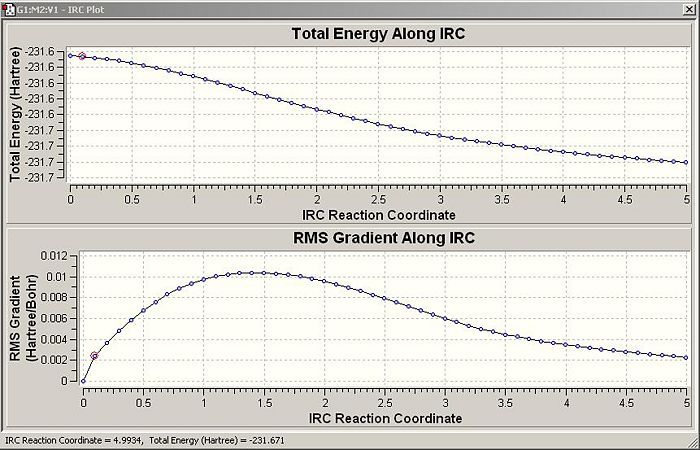
The second method, in which 200 points were calculated rather than 50, took more than 5 hours on the super computer network and though it did follow the conformers relaxation after bonding significantly further, it still did not reach the absolute lowest energy conformer as the graph below reveals (it does however reach a local minimum at roughly IRC reaction coordinate 12) .

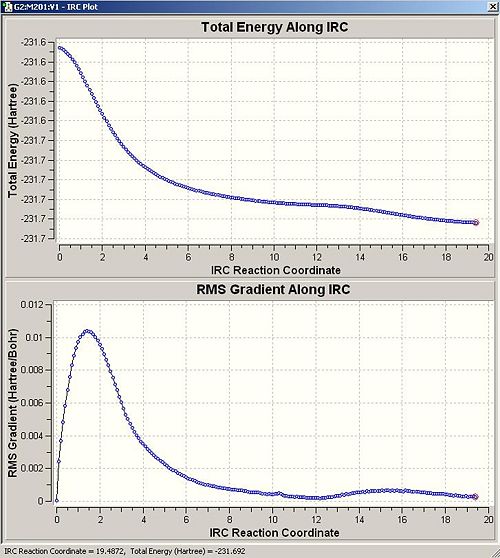
Consequently this method was abandoned as too expensive in computer time and the result of method one will be employed.

The Activation Energies

The activation energy is by definition the difference in energy between the starting material and the transition state. In order to be able to compare the energy calculated of two transition geometries, the boat and the chair, they must be optimised to the small level of theory as the starting material. Consequently they were both the computed transition state geometries were optimised to a B3LYP/6-31G* level of theory.

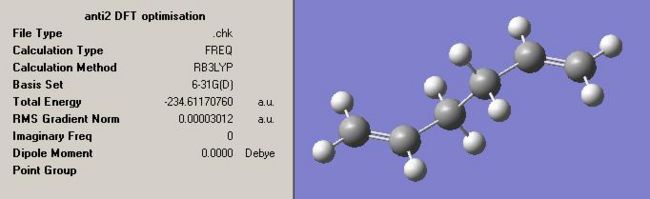
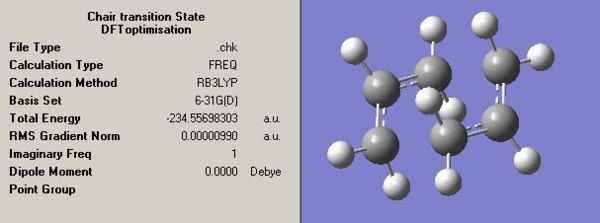
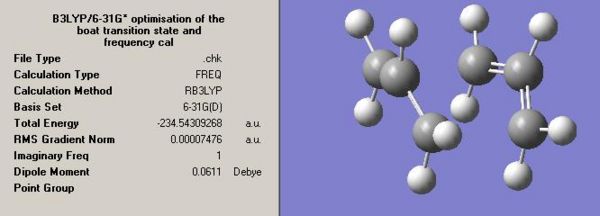
Anti2 Optimised Energies

Sum of electronic and zero-point Energies= -234.469195 a.u.

Sum of electronic and thermal Energies= -234.461847 a.u.

Sum of electronic and thermal Enthalpies= -234.460903 a.u.

Sum of electronic and thermal Free Energies= -234.500782 a.u.

Chair Transition State DFT Optimised Energies

Sum of electronic and zero-point Energies= -234.414930 a.u.

Sum of electronic and thermal Energies= -234.409009 a.u.

Sum of electronic and thermal Enthalpies= -234.408065 a.u.

Sum of electronic and thermal Free Energies= -234.443815 a.u.

Boat Transition State DFT Optimised Energies

Sum of electronic and zero-point Energies= -234.402340 a.u.

Sum of electronic and thermal Energies= -234.396002 a.u.

Sum of electronic and thermal Enthalpies= -234.395057 a.u.

Sum of electronic and thermal Free Energies= -234.431101 a.u.

The transition State at 0K


The conformer	Energy (a.u.)	Energy (KJMol-1)	Energy (KCalMol-1)
anti2	-234.469195	-615598.8715	-147131.6614
Chair TS	-234.41493	-615456.3987	-147097.6096
Boat TS	1.37004	1.37080	-147097.6096
Chair Activation Energy	0.054265	175.5278025	41.95215162
Boat activation energy	0.066855	142.4727575	34.05180627

These values compare do not compare very well with the literature values for the activation energy of the two conformers, 33.5 ± 0.5 KCalMol-1 for the chair and 44.7 ± 2.0 KCalMol-1. The predicted values are similar and certainly of the same order of magnetude but both the chair and the boat activation energies are predicted to be lower than they have been measured.

The Diels Alder Cycloaddition Investigation

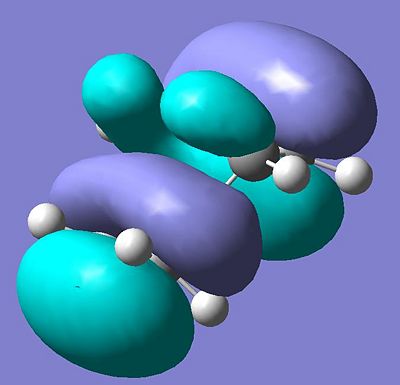
cis butadiene was drawn using gaussview and optimised using a semi-empirical method at a AM1 level of theory. The calculated molecular orbital surfaces were calculated and the HOMO and the LUMO are shown below.

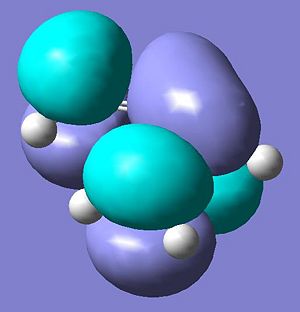
The molecular orbitals of ethene were calculated via the same method and are shown below.

Consequently, the HOMO on the cis butadiene are at the correct symmetry to interact with the LUMO on the ethene and the LUMO molecular orbitals on the cis butadiene are the correct symmetry to interact with the HOMO on the ethene.

According to frontier molecular orbital theory (which only considers the highest occupied and lowest unoccupied orbitals) the reaction is allowed as HOMOs and LUMOs must of the same symmetry to interact.

The transition state

Different methods will now be employed to calculate the transition state geometry. The first method will involve guessing the approximate transition state from prior knowledge as to how the reaction would be expected to proceed.

The terminal carbons were lined up with a staggering consistent with donation into the pi-antibonding orbital (i.e. roughly 109°)with an interatomic distance of roughly 2.2Å. This guess geometry should be close enough to the actual transition state to allow the program to find the transition state by computing the Hessian.

Three methods used will be the optimisation to a berny, the frozen coordinate method and the QST2 method. The first method takes less computational work but is more prone to getting stuck in a local minimum.

Method 1

The initial guess transition state geometry was used to calculate a probable transition state by computing the hessian. The Geometry is shown below.


The geometry of the predicted transition state	The frequencies of the predicted transition state

The method produced a geometry that was consistent with my expectations of what the transition state would be like. It had a single negative frequency, corresponding the to the vibration the brought the ends of the terminal carbons together and that shortened the central C-C bond in the diene (consistent with the formation of a double bond). The bond lengths produced are 2.20879Å and 2.21021Å between the terminal carbons and vibrational frequency of the 818.619 cm^-1

Method 2

The second method involves freezing the bond lengths between the terminal carbons optimising, and then relaxing this restriction and reoptimising.


The geometry of the predicted transition state	The frequencies of the predicted transition state

This method produced a geometry which seems unlikely. The interatomic distance between the terminal carbons is extremely short; just 1.55434Å for both, and the bond length between the central 2 atoms in the dine is also very short, just 1.31770Å. I believe this geometry is that of the product, not the transition state considering that theses two parameters are identical to those in the product molecule optimised under the same level of theory. Another piece of evidence to support the theory that this is not in fact a transition state geometry is that there exists no imaginary vibrational frequency corresponding to the process.

Method 3

The third method is the QTS2 method in which the computer interpolates the transition state from the starting materials and the final product. This is computationally expensive but fairly reliable.


The geometry of the predicted transition state	The frequencies of the predicted transition state

The geometry produced seems to lie within the bounds of my expectations. The inter-atomic distances between the terminal carbons were 2.21109Å and 2.20800Å, and the C-C bond lengths within butadiene 1.37-1.39Å which is constant with a bond order of 1.5, what would be expected in the transition state. In addition there is an imaginary vibrational frequency at 818.418cm-1. For these reasons I am fairly confident that this is an appropriate transition state geometry and will hence use the molecular orbitals calculated from this method to analyse.

Explanation of the shape of the HOMO in the transition state


The transition state	The predicted HOMO of the transition state

The HOMO is symmetric with respect to the plane of symmetry outlined earlier and if compared to the previously drawn orbitals it is clearly the linear combination of the HOMO on ethene and the LUMO on the diene. Consequently it can be said that the HOMO on in ethene is closer in energy to the LUMO in the diene than the HOMO on the diene is to the LUMO in ethene. This corresponds very well to what a chemist would intuitively expect; a conjugated system is lower in energy, so will hence have a HOMO too low to interact with the LUMO in an unconjugated pi-system (or at least it would prefer the interaction observed).

Study the regioselectivity of the Diels Alder Reaction

Cyclohexa-1,3-diene 1 undergoes facile reaction with maleic anhydride 2 to give primarily the endo adduct (see below).

The transition state to both the endo and the exo product will be modelled to try and show that the endo product is favoured because the transition state is higher in energy; i.e the selectivity in kinetically controlled.

The QTS2 method was used to predict the transition states. First both the reactants and products were optimised using the HF/3-21G level of theory. The reactants were arranged in a good approximation (judged by our prior expectations about orbital overlap) to the predicted transition state (endo for the endo product and exo for thee exo product). The calculation was then set up and run as described in the tutorial.

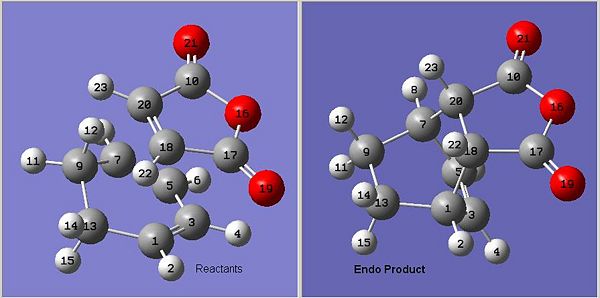
The optimised transition states were returned and checked to see if they were consistent with our expectations for the transition state or whether the computation had erroneously found a local minimum.

Predicted Transition State Analysis

Of the two transition states produced the endo had the lowest energy (-605.61036817 a.u.) whereas the exo isomer had an energy of -605.60359125 a.u.


	The exo conformer	The endo conformer
	an image of the exo transition state	an image of the endo transition state
Bond	Exo Bond Length (Å)	Endo Bond Length (Å)
C20-C7	2.26074	2.23047
C7-C9	1.51882	1.51768
C7-C5	1.37004	1.37080
C5-C3	1.39759	1.39620
C1-C18	2.26068	2.23134
C18-C20	1.37313	1.37006
C9-C12	1.55882	1.56019
C1-C12	1.51883	1.51771
C20-C17	1.48144	1.48074
C17-O15	1.39552	1.39413
015-C16	1.39552	1.39409
016-C18	1.48144	1.48081


Comment	Exo C-C interatomic distance (Å)	Endo C-C interatomic distance (Å)
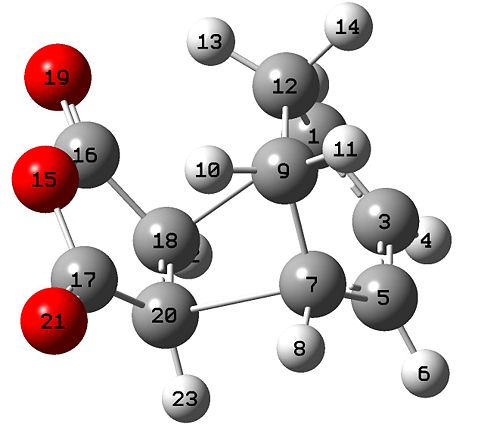
The extra hydrogen substitutents force the two carbons in the Exo transition further away than the equivilent carbon in the endo transition state	C17-C9 2.91627	C17-C3 2.84814
Again, the extra hydrogen substitutents force the two carbons in the Exo transition further away than the equivilent carbon in the endo transition state	C16-C12 2.91629	C16-C5 2.84746

The Relative Energies of the Exo and Endo Transition States

Exo Optimised Energies

Sum of electronic and zero-point Energies= -612.498013 a.u.

Sum of electronic and thermal Energies= -612.487663 a.u.

Sum of electronic and thermal Enthalpies= -612.486719 a.u.

Sum of electronic and thermal Free Energies= -612.534261 a.u.

Endo Optimised Energies

Sum of electronic and zero-point Energies= -612.502142 a.u.

Sum of electronic and thermal Energies= -612.491788 a.u.

Sum of electronic and thermal Enthalpies= -612.490843 a.u.

Sum of electronic and thermal Free Energies= -612.538329 a.u.

Starting Material Optimised Energies

Reactant 1

Sum of electronic and zero-point Energies= -233.296105 a.u.

Sum of electronic and thermal Energies= -233.290933 a.u.

Sum of electronic and thermal Enthalpies= -233.289989 a.u.

Sum of electronic and thermal Free Energies= -233.324353 a.u.

Reactant 2

Sum of electronic and zero-point Energies= -379.233654 a.u.

Sum of electronic and thermal Energies= -379.228470 a.u.

Sum of electronic and thermal Enthalpies= -379.227526 a.u.

Sum of electronic and thermal Free Energies= -379.262726 a.u.

The transition State at 0K


The conformer	Energy (a.u.)	Energy (KJMol-1)	Energy (KCalMol-1)
Starting materials	-612.529759	-1608196.882	-384368.2795
Endo TS	-612.502142	-1608124.374	-384350.9495
Exo TS	-612.498013	-1608113.533	-384348.3586
Endo Activation Energy	0.004129	10.8406895	2.590986973
Exo activation energy	0.031746	83.349123	19.92091849

As the reaction is under kinetic control, the significantly lower activation energy for the endo product strongly suggests that the most favoured product will be the endo product via a large margin. The reasons for the the lower energy of the transition state are partly sterics and partly secondary orbital interactions and are discussed below.

Secondary Orbital Overlap Effects

The above shorter inter atomic distances in the Endo product can be explained in terms of sterics but also in terms of an orbital interaction between the antibonding orbitals of carbons 3 and 5 (which are the same as the bonding orbitals between carbons 3&1 and 5&7 see below) with the pi antibonding orbital of the carbonyl group.

This is illustrated below.

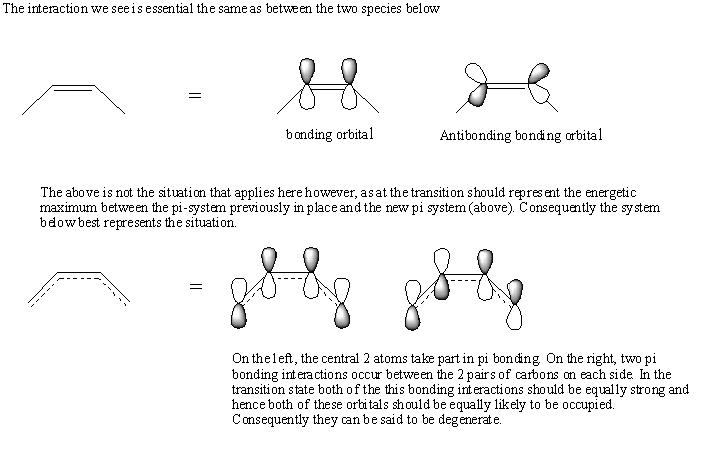
(note that the fully bonding and fully antibonding orbitals are not shown because there is no question as to their occupancy (yes and no respectfully).

I believe that the pi bonding/antibonding orbital on the right will interact with the pi anti boning orbitals in the carbonyl groups in the endo product. Only the interaction of occupied orbitals will lead to greater stabilisation, and because as I explained above, the the orbital can be thought of as occupied because the bond between carbons 3 and 4 has only a bond order of 1.5 and hence will have an antibonding pi orbital that is partially filled, and it this orbital that will interact.

Consequently, the interaction between the partially occupied C-C pi antibonding orbitals on the endo transition state with the pi antibonding orbitals in the carbonyl groups will bring stabilisation to the overall energy in the molecule as well as alter the geometry so that the respective interatomic distances discussed previously will be shorter.

The HOMO of the endo transition state was predicted to see if this stabilisation is indeed as predicted.

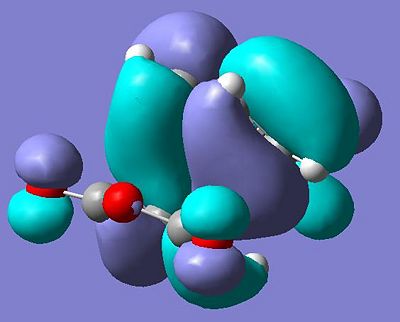
From inspection of my HOMO I can conclude that my initial assessment of the interaction was correct. On a basic level the symmetry is correct; it is antisymmetric with respect to the mirror plane the runs through the transition state. Also the orbitals discussed are clearly visible(though as would be expected the lobes that constructively interact have merged). on of the partially filled π bonding orbitals on carbons 7-5-3-1 are donating electron density into the C=O π* orbital and that is being manifested physically as an attractive interaction between these carbons and the backside of the carbonyl group. This will stabilise the transition state as well as reducing the corresponding interatomic distance.

Extension: Investigation into the Concertion of a Published example

A Variant on the following reaction was investigated.

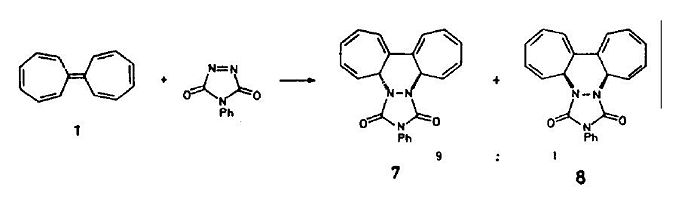
The paper in which this reaction is outlined can be found here;

http://dx.doi.org/10.1016/0040-4039(81)80058-5

It can be found here and is an example of a cycloaddition with an antarafacial component; it is a 4N electron process and occurs under heating. The reaction is suggested in the paper to be asynchronous and has been subsequently suggested to be fully stepwise:

http://www.ch.ic.ac.uk/local/organic/pericyclic/p1_cyclo.html

Due to computation time the second reactant will be substituted for ethyne which is significantly less complex to model. The overal reaction will be investigated (briefly) because so far we have not covered an example which is a 4N electron process, or one in which the is an antarafacial component. In addition it has been suggested that the process is so asynchronous that is actually stepwise and this will be investigated via IRC modelling of the reaction process. In addition the activation energy will be calculated.

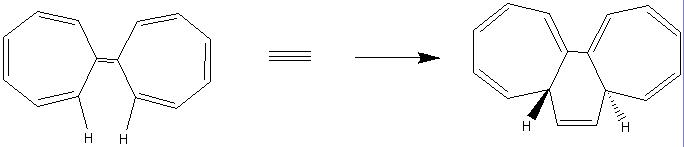
The modified reaction that will be investigated

Calculating the Transition State

The Reactants and the products were optimised to a HF/3-21G level of theory and were renumbered so that the same atoms corresponded to each other.

A QTST2 computation was then run to predict the transition state between the reacts and the product. I felt it was necessary to run a QTST2 TS calculation because the complexity of the molecule and the fact I had little confidence in any estimation I could make of the transition state meant that the other less involved methods were likely to give me incorrect answers. I always knew this level of optimisation would come at the expense of computational time but hoped that as the reactants were both planer and hence very geometrically restricted, this would not be prohibitive. Unfortunately the calculation ran for a long time. The reaction was submitted to SCAN and left to run. It ran for 72 hours until today (21/11/08) when I terminated as I felt it would be unfair to use the computer time while the second group also require the supercomputer network. Frustratingly, this means that I cannot display a transition state geometry, an activation energy or view the likely reaction progression using IRC modelling.

The Energies of the Product and Reactants

The product and the reactents were were optimised to a B3LYP/6-31G* level of theory so that a more accurate representation of the geometries and the energy could be obtained. These are displayed below.

The Alkyne

Sum of electronic and zero-point Energies= -77.299012

Sum of electronic and thermal Energies= -77.296080

Sum of electronic and thermal Enthalpies= -77.295136

Sum of electronic and thermal Free Energies= -77.318039

Pentahelicene

The Conjugated Cyclic Reactent

Sum of electronic and zero-point Energies= -540.393335

Sum of electronic and thermal Energies= -540.384333

Sum of electronic and thermal Enthalpies= -540.383389

Sum of electronic and thermal Free Energies= -540.426761

Pentahelicene

The Product

Sum of electronic and zero-point Energies= -617.690496

Sum of electronic and thermal Energies= -617.678363

Sum of electronic and thermal Enthalpies= -617.677419

Sum of electronic and thermal Free Energies= -617.727533

Pentahelicene

The Enthalpy of the Reaction at 0K

Consequently the enthalpy of the reaction can be said to be -0.00185 a.u. (-4.8598KJmol-1). This is rather small so the reaction can be considered to be in equilibrium (the heat energy at room temperature is roughly 2.5KJmol-1).

Further Work

If I had additional time, I would have liked to run the transition state optimisation to completion. The Computational tiem could be reduced by he use of a QST3, but this would also reduce the usefulness of the calculation; the reason why this reaction was investigated was to compute whether the process is concerted or stepwise, inserting a TS guess would directly affect the result in this respect. To get around this I could perform the calculation twice, one with a concerted transition state and once with a transition state consistent with a stepwise transition state. Which ever process has the lowest activation energy will be the favoured mechanism. The disadvantage with this technique is that it will require a series of QTS3 calculations and hence may not take significantly less computer time.