Rep:Mod:sdaw6262
Module 1: Structure and Spectroscopy (Molecular Mechanics and Molecular Orbital)
Introduction
Molecular mechanics can be used to predict the likely products from a reaction through thermodynamic reasoning. By examining the relative stabilities of the possible products and reactants, the thermodynamically controlled reaction products are revealed. The process of modelling molecular structures is highly useful in research chemistry, for instance it is commonplace for a reaction to give mixtures of isomers, e.g. diastereoisomers, and by knowing the relative energies of the two diastereomers one may engineer the reaction conditions in such a way as to produce exclusively the isomer of interest. Another use of molecular mechanics is that the stereoselectivity of a reaction can often be determined by observation of steric interactions within the starting material, so it is possible to apply this technique not only quantitatively but qualitatively as well.
The program used here is ChemBioUltra3D. Within ChemBioUltra3D can be found MM2, a molecular mechanics program that has been used here for geometry optimisations. MM2 accomplishes this by considering bond stretching, bending and torsion as well as Van der Waals' forces, dihedral angles, dipole interactions, and then altering the molecule's shape in small iterative steps until its energy reaches a minimum. All of the 'Jmols' shown in this section are the result of the molecule in question having undergone an MM2 optimisation.
The Hydrogenation of Cyclopentadiene Dimer
Endo Dimer
Endo |
Exo Dimer
Exo |
Minimised Energies
| Interaction | Energy of endo | Energy of exo |
|---|---|---|
| Stretch: | 1.2454 | 1.2923 |
| Bend: | 20.8603 | 20.5870 |
| Stretch-Bend: | -0.8320 | -0.8413 |
| Torsion: | 9.5039 | 7.6715 |
| Non-1,4 VDW: | -1.5083 | -1.4358 |
| 1,4 VDW: | 4.3012 | 4.2320 |
| Dipole/Dipole: | 0.4448 | 0.3778 |
| Total Energy: | 34.0153 kcal/mol | 31.8834 kcal/mol |
| Total Energy: | 0.0542 Hartree | 0.05081 Hartree |
The exo conformation of cyclopentadiende is found to be the lowest in energy. The difference in total energy is mostly down to the torsion energy difference indicating less torsional strain in the exo conformer. The higher torsional strain of the endo conformer can be observed on account of its shape as the two rings are locked into a c-shape, which entails a certain degree of strain to maintain such a shape. Whereas the exo bicyclic system takes a z-shape. Since the endo dimer is produced on dimerisation of cyclopentadiene and this is the thermodynamically less stable product then the reaction must be kinetically controlled, i.e. the reaction pathway leading to the endo dimer must have a lower energy transition state. See A. Kumar and S. S. Pawar[1], for more information. A limitation of molecular mechanics presents itself here in that the energy of the transition state cannot be calculated rendering it impossible to predict the outcome of a kinetically controlled reaction with just the knowledge of the energies of the products.
The endo dimer can be hydrogenated at two different positions to yield the molecules shown below.
Product 3
Product3 |
Product 4
Product4 |
Minimised Energies
| Interaction | Energy of Product 3 | Energy of Product 4 |
|---|---|---|
| Stretch: | 1.2067 | 1.0963 |
| Bend: | 18.8637 | 14.5075 |
| Stretch-Bend: | -0.7528 | -0.5493 |
| Torsion: | 12.2396 | 12.4972 |
| Non-1,4 VDW: | -1.5532 | -1.0507 |
| 1,4 VDW: | 5.7649 | 4.5124 |
| Dipole/Dipole: | 0.1632 | 0.1407 |
| Total Energy: | 35.9322 kcal/mol | 31.154 kcal/mol |
| Total Energy: | 0.0573 Hartree | 0.0496 Hartree |
Hydrogenation of the endo dimer yields two structural isomers 3 and 4. Isomer 4 is the thermodynamically most stable isomer indicating that the double bond in the bridged 5-membered ring is the most readily hydrogenated out of the two. The difference in total energy between 3 and 4 is mostly down to the bending energies, all other energy components are very similar. The difference in stability is due to the postion of the bridge in relation to the alkene. The conversion of an sp3 hybridised centre to an sp2 centre restricts the ring's movement. The presence of the bridge already makes the ring which it bridges quite strained so the reduction in rotational freedom and a constriction of the C-C bond that becomes the alkene accentuates this. It can be seen that the bond angles in product 3 are 107.2 degrees, closer to that expected at an sp3 centre rather than the 120 degree bond angle typical for alkenes. This small bond angle results in a large strain and is a consequence of the bridging carbons, which pull the tertiary carbons that it is connected to closer together, locking the alkene into an elongated 5-membered ring. Whereas in isomer 4, the carbon-carbon alkene bond angle is larger at 112 degrees with a resultant reduction in strain.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring
Product 5 (first optimisation)
Product5 |
Product 5 (second optimisation)
Product5 |
Product 7 (first optimisation)
Product7 |
Product 7 (second optimisation)
Product7 |
Minimised Energies
| Interaction | Energy of 5 (1st opt) | Energy of 5 (2nd opt | Energy of 7 (1st opt) | Energy of 7 (2nd opt) |
|---|---|---|---|---|
| Stretch: | 1.2030 | 1.1901 | 1.7248 | 1.7727 |
| Bend: | 11.7259 | 11.6255 | 10.6239 | 9.5401 |
| Stretch-Bend: | 0.0538 | 0.0568 | 0.4006 | 0.4024 |
| Torsion: | 4.8237 | 4.8511 | -5.9913 | -6.2463 |
| Non-1,4 VDW: | -1.7957 | -1.9572 | -0.9981 | -1.2728 |
| 1,4 VDW: | 11.9745 | 11.8778 | 18.0644 | 17.8667 |
| Charge/Dipole: | 2.6213 | 2.6734 | 2.5839 | 2.5455 |
| Dipole/Dipole: | -4.0134 | -3.9753 | -4.8116 | -4.7855 |
| Total Energy: | 26.5931 kcal/mol | 26.3422 kcal/mol | 21.5966 kcal/mol | 19.8228 kcal/mol |
| Total Energy: | 0.0424 Hartree | 0.0420 Hartree | 0.0344 Hartree | 0.0316 Hartree |
Methylmagnesium iodide cannot be computed using ChemBio3DUltra because it is an inorganic molecule. The parameters used in
MM2 cover elements typical of organic molecules.
In both of compounds 5 and 7 the carbonyl oxygen points slightly above the plane of the aromatic ring. By doing so the oxygen maintains a slightly staggered position relative to the hydrogen para to the nitrogen of the pyridinyl ring, minimising the Van der Waals' repulsion. The second optimisation of both compounds corresponds to an increase in the degree of staggering and is reflected by the lower total energies. For compound 5 there is an increase in the dihedral angle from the oxygen to the the carbon in the para position in the pyridinyl ring from 22.8 after the first optimisation to 23.5 after the second. The second optimisation of compound 7 reveals a significant reduction in the bending energy as the major stabilising effect which appears to relate to a twisting in conformation of the two methyl groups connected to the nitrogen of the amide..
In the reaction of compound 5 with methylmagnesium iodide there are two possible diastereomeric products. The diastereomer with the methyl up is major (product 6). This can be explained by the mechanism of reaction. The methylmagnesium iodide chelates the carbonyl oxygen via magnesium, since the carbonyl points above the pyridine ring then the chelation also occurs above the ring. The reaction proceeds “via a six-centred transition state” resulting in methylation above the ring[2].
In the reaction of compound 7 with aniline there are once again two possible diastereomers produced, the aniline can be up or down in the product. The major diastereomer is the one with the aniline substituent up. This is most likely due to repulsion between the lone pair of nitrogen and those on the carbonyl oxygen and could be regarded as a type of atrop-diastereoselectivity. Another diastereoselective mechanism consquent of the position of this carbonyl is shown in the reaction of sodium borohydride with a quinolinium salt in which diborane complexes the salt leading to attack of the face that is not sterically hindered by the complexation[3].
The explanations proposed for this diasteroselection does not take into account molecular orbital theory. The interaction of frontier molecular orbitals in particular may provide an alternative way of understanding the mechanisms of these reactions.
Stereochemistry and Reactivity of an Intermediiate in the Synthesis of Taxol
Product 10
Product10 |
Saturated product 10
Satproduct10 |
Product 11
Product11 |
Saturated product 11
Satproduct11 |
Minimised Energies
| Interaction | Energy of 10 | Energy of saturated 10 | Energy of 11 | Energy of saturated 11 |
|---|---|---|---|---|
| Stretch: | 3.0370 | 5.0084 | 2.5429 | 4.5744 |
| Bend: | 18.4779 | 27.0850 | 11.7052 | 23.4356 |
| Stretch-Bend: | 0.4010 | 1.0859 | 0.3898 | 1.1318 |
| Torsion: | 19.9647 | 19.9946 | 19.0373 | 19.5626 |
| Non-1,4 VDW: | -0.5443 | 2.1428 | -0.8732 | 2.4104 |
| 1,4 VDW: | 13.6181 | 17.8323 | 12.4412 | 16.8445 |
| Dipole/Dipole: | 0.0054 | 0.0000 | 0.1432 | 0.0000 |
| Total Energy: | 54.9599 kcal/mol | 73.1489 kcal/mol | 45.3864 kcal/mol | 67.9595 kcal/mol |
| Total Energy: | 0.0876 Hartree | 0.1166 Hartree | 0.0723 Hartree | 0.1083 Hartree |
Compound 11 has a much lower energy than compound 10 and is therefore the most stable conformation. The bending energy is the most significant factor here and is much higher for 10 because the up position of the carbonyl forces the cyclohexyl substituent downwards. The saturated versions of 10 and 11 are much higher in energy due to the greater number of conformations possible with the absence of the C=C double bond to restrict rotation. The alkene in both 10 and 11 will likely react slowly because of the steric hindrance from the methyl group on the bottom face and the vicinal CH2’s on the top face. In addition to this, in isomer 11 the carbonyl oxygen is pointing downwards so attack from the bottom face may be disrupted due to attraction to the lone pairs on oxygen by an attacking electrophile.
Room Temperature Hydrolysis of a Peptide
OH down, axial
OHdownaxial |
OH down, equatorial
OHdownequatorial |
OH up, axial
OHupxaial |
OH up, equatorial
OHupequatorial |
Minimised Energies
| Interaction | Energy of OH down, axial | Energy of OH down, equatorial | Energy of OH up, axial | Energy of OH up, equatorial |
|---|---|---|---|---|
| Stretch: | 1.6364 | 1.7146 | 1.5273 | 1.4839 |
| Bend: | 8.1989 | 5.1912 | 5.0643 | 3.8106 |
| Stretch-Bend: | 0.6428 | 0.5290 | 0.5487 | 0.5073 |
| Torsion: | 11.9830 | 9.3527 | 9.0035 | 7.6762 |
| Non-1,4 VDW: | -8.0034 | -7.3803 | -7.1003 | -7.1007 |
| 1,4 VDW: | 10.2222 | 10.0244 | 9.6219 | 9.9019 |
| Dipole/Dipole: | -4.8540 | -6.3006 | -6.5910 | -6.5819 |
| Total Energy: | 19.8258 kcal/mol | 13.1311 kcal/mol | 12.0744 kcal/mol | 9.6972 kcal/mol |
| Total Energy: | 0.0316 Hartree | 0.0209 Hartree | 0.0192 Hartree | 0.0155 Hartree |
In all cases the conformers where the amide group is axial, the total energy is higher due to the large size of the group causing in a large 1,3 repulsion. In the cases where the conformer’s OH group hydrogen bonds with the oxygen of the amide, the nucleophilic oxygen of the hydroxyl group is tied up by the hydrogen bonding so is unlikely to attack the carbonyl carbon because the electron density of the nucleophilic oxygen is concentrated away from the amide group as the hydrogen bond occurs via donation of electron density from the amide nitrogen so that the hydrogen of the OH group points towards the amide rather than the lone pairs, these conformations will therefore not be considered here. The isomer with the hydroxyl group down reacts most quickly to form the ester because in this position it can react with the equatorially positioned amide. However if the hydroxyl group is up then the amide group must be axial for reaction to occur, whereby a simple rotation of the C- (ring)N bond yields a reactive conformation. An addition to the activation energy in rearrangement from the equatorial conformer (11.9980 kcal/mol) to the thermodynamically less stable axial isomer conformer (17.1367 kcal/mol) is thus required so the rate of reaction is lower. The half-lives of both reactions are relatively short for a few reasons. The nucleophilic and electrophilic centres are already close together compared to straight chain molecules where the reacting centres may be at opposite ends of the molecule. The close proximity of the reacting centres allows for hydrogen bonding to occur which brings these centres even closer together. The most stable hydrogen bonded conformation is always the one with an oxygen-oxygen hydrogen bond wherein the hydroxyl shares its hydrogen with the carbonyl oxygen, lowering the energy of the pi* orbital making it accept the lone pair from the hydroxyl more readily (or the carbonyl carbon is more acidic); furthermore the lone pair on the hydroxyl oxygen is more basic due to the partially ‘donated’ hydrogen making the hydroxyl more nucleophilic.
Modelling using semi-empirical molecular orbital theory
Dichlorocarbene
Dichlorocarbene |
Hydrogenated Product
chlorocarbene |
IR Vibrational Frequencies
| Dicarbene/Carbene | Vibration No. | Frequency/(1/cm) | Intensity | Functional Group/Bond |
|---|---|---|---|---|
| Dicarbene | 19 | 772.545 | 25.28 | C-Cl |
| Dicarbene | 55 | 1740.9 | 4.155 | C=C (Anti to C-Cl)) |
| Dicarbene | 56 | 1762.01 | 3.8961 | C=C ('Syn' to C-Cl) |
| Carbene | 19 | 776.881 | 20.278 | C-Cl |
| Carbene | 60 | 1761.67 | 4.289 | C=C ('Syn' to C-Cl) |
These results make it possible to see which of the alkenes has been hydrogenated. Clearly the one anti to C-Cl has been hydrogenated since the alkene stretch remaining in the hydrogenated product is almost identical (1761.67 per cm versus 1762.01 per cm) to the alkene in the 'syn' position in dichlorocarbene.
MO's of Dichlorocarbene
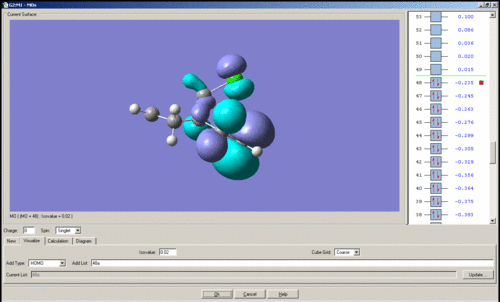

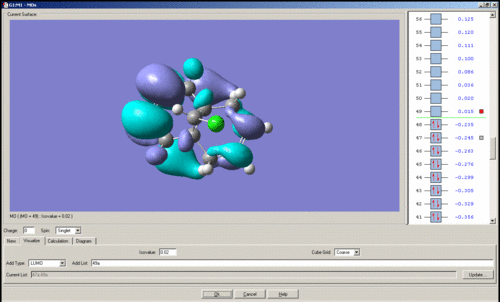
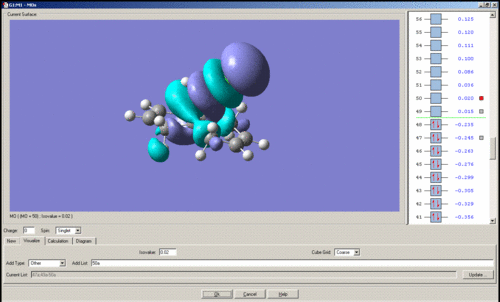
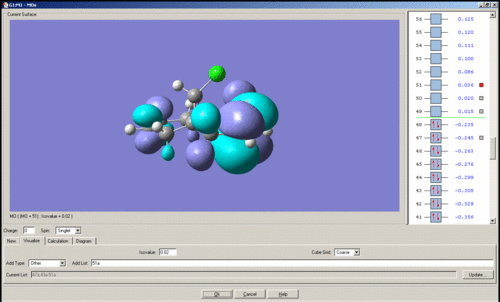
Mini project using DFT MO Methods
Introduction
Whereas molecular mechanics took a more classical approach, density functional theory (DFT) utilises quantum theory. The calculations are more complex and consequently take significantly longer to carry out. The calculation method generally used here is mPW1PW91 with a 6-31G basis set, which is a low basis set and one of the simpler calculation methods.
NMR Spectroscopy can be a highly useful analytival tool to distinguish one isomer of a acompound from another. However, the chemical shifts present in the spectra of some isomers may be almost identical, which is where coupling constant data come into play. A coupling constant depends on a dihedral angle in a molecule and by using the Karplus equation such an angle can be determined allowing isomeric identification.
The reaction below can yield two diastereoisomers, but predominantly the alpha-anomer which is illustrated below where the cyclopropyl ring is syn to the acetate para relative to it. The beta-anomer shows an anti relationship between the aforementioned acetate and cyclopropyl ring.
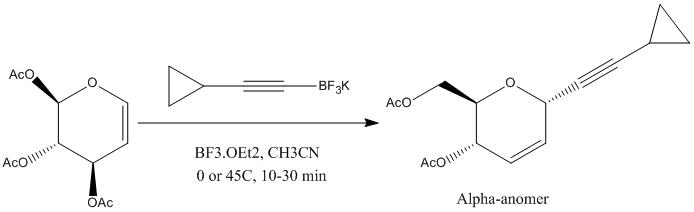 [4]
[4]
13C NMR Chemical Shift Calculation
The geometries of both diastereomers were first optimised to yield the molecules shown below before the NMR predictions were made.
(Alpha anomer: Geometry optimisation and vibrational frequencies DOI:10042/to-1035 , NMR calculation DOI:10042/to-1037 ) (Beta anomer: Geometry optimisation and vibrational frequencies DOI:10042/to-1036 , NMR calculation DOI:10042/to-103? )
Alpha Anomer
Alphaanomer |
Beta Anomer
Betaanomer |
Minimised Energies
| Interaction | Energy of Alpha Anomer | Energy of Beta Anomer |
|---|---|---|
| Stretch: | 1.4361 | 1.4310 |
| Bend: | 5.7114 | 6.3965 |
| Stretch-Bend: | 0.5580 | 0.6680 |
| Torsion: | -1.2160 | -1.0534 |
| Non-1,4 VDW: | -3.6785 | -3.0442 |
| 1,4 VDW: | 11.3570 | 14.0219 |
| Dipole/Dipole: | 2.7946 | 7.9763 |
| Total Energy: | 24.8092 kcal/mol | 27.7899 kcal/mol |
| Total Energy: | 0.0395 Hartree | 0.0443 Hartree |
Generally, the alpha anomer of compounds with a heteroatom attached to the anomeric carbon are thermodynamically more stable than the corresponding beta anomer due to the anomeric effect whereby there is donation of the lone pair on the ring oxygen into the σ* orbital of the C-Het bond, which can only occur when the heteroatom occupies an axial position. This electronic stabilising effect counters the increased steric hindrance due to 1,3-compression.
The alpha anomer is the most stable in this case too, however this time there can be no anomeric stabilisation due to the lack of a heteroatom. But this is not surprising since the 1,3-compression is probably similar for both isomers as although carbon is larger than hydrogen, the C-C bond (1.476A) in the alpha anomer is longer than the C-H bond (1.115A) in the beta anomer in the at the axial position on the anomeric carbon. The carbon attached to the anomeric carbon in the alpha anomer is also more staggered relative to the nearest hydrogen in the 1,3 position than the corresponding hydrogen in the beta anomer. The energy difference is primarily due to diope-dipole and 1,4-Van Der Waals' interactions.
Literature Chemical Shifts for NMR of Alpha Anomer
13C NMR (75 MHz, CDCl3) δ 8.4, 20.8, 21.0, 24.8, 63.1, 64.2, 64.8, 67.9, 69.6, 71.0, 90.8, 124.8, 129.9, 170.3, 170.9[5]
Calculated Chemical Shifts for NMR of Alpha Anomer
13C NMR, reference= TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO, δ 2.5, 11.7, 12.1, 20.9, 22.1, 63.8, 66.9, 67.1, 67.2, 68.8, 89.8, 124.3, 128.1, 165.6(171.2), 166.6(172.1)
Note: the calculated values for the chemical shifts of the carbonyl carbons were corrected by applying the formula, δcorr = 0.96δcalc + 12.2. The corrected results are given in brackets next to the raw data.
Literature:δ 8.4, 20.8, 21.0, 24.8, 63.1, 64.2, 64.8, 67.9, 69.6, 71.0, 90.8, 124.8, 129.9, 170.3, 170.9
Calculated:δ 2.5, 11.7, 12.1, 20.9, 22.1, 63.8 66.9, 67.1, 67.2, 68.8, 89.8, 124.3, 128.1, 171.2, 172.1
The experimental shift at 8.4, which corresponds to the carbon connecting the cyclopropyl to the alkyne has a much lower calculated shift. Thisd indicates that the anisotropic effect of the pi-electrons which will cause this carbon to experience increased deshielding has not been fully accounted for by the calculation method, a possible limitation of the software. The same situation applies to the shifts at 20.8 and 21.0 which are the other two cyclopropyl carbons. Although there are other possibilities for the orientation of the cyclopropyl ring, it is very unlikely that the chemical shifts of its carbons would change by much because the anisotropic effect of the alkyne would be unchanged as the cyclopropyl can only rotate about the C-C alkyne axis so the angle that the effect is dependent upon would be unchanged. The other possibility is in the ring being slightly closer to some of the oxygens, but they are too far away to have any observable effect. The emboldened chemical shift appears to be wrongly reported since the two calculated values of 20.9 and 22.1 are of the carbons of the two acetate methyl groups and as such one would expect these two shifts to be almost identical as calculated, however the two respective literature values are 24.8 and 63.1. The remainder of the chemical shifts are in good agreement.
Dihedral Angles
There is only one dihedral angle which differs in the two isomers and that is between the hydrogen on the carbon that the alkyne is joined to on the 5-membered ring and the hydrogen on the adjacent carbon of the alkene. As the dihedral angle increases from 0 degrees to 90 degrees the coupling constant decreases, reaching a minimum at 90 degrees and a maximum when the hydrogens are eclipsed and anti-periplanar. Since this angle is larger in the beta anomer then the (closer to 90 dgrees) then coupling constant will be smaller.
| Anomer | Dihedral Angle/degrees | 3-J Coupling constant/Hz |
|---|---|---|
| Alpha | -52.18631 | 2.9158 |
| Beta | 73.98297 | 0.3674 |
The literature value for the alpha anomer coupling constant is 3.27Hz which is quite close to the theoretical value. The difference may be due to a slighlty inaccurate conformation. However, the difference between the two predicted coupling constants is large enough that even if the conformations are not quite right the isomers should still be distinguishable by this particular coupling constant. Some of the other coupling constants will vary slightly, but this one is the most reliable for identification purposes.
IR Vibrational Frequencies
| Alpha/Beta | Vibration No. | Frequency/(1/cm) | Literaure frequency/(1/cm) | Intensity | Functional Group/Bond |
|---|---|---|---|---|---|
| Alpha | 87 | 1738.83 | 1740 | 0.5632 | Alkene C=C stretch |
| Alpha | 90 | 2344.85 | 2359 | 56.7794 | Alkyne stretch |
| Alpha | 62 | 1211.31 | 1207 | 37.0683 | Alkene C-H scissoring |
| Alpha | 91 | 3027.22 | 2957 | 14.7184 | H-COC stretch, cyclic ether, furthest from alkyne |
| Alpha | 92 | 3037.96 | 3032 | 17.4525 | H-COC stretch, cyclic ether, closest to alkyne |
| Beta | 87 | 1737.33 | 1740 | 3.282 | Alkene C=C stretch |
| Beta | 90 | 2359.33 | 2359 | 64.6695 | Alkyne stretch |
| Beta | 64 | 1210.25 | 1207 | 29.4019 | Alkene C-H scissoring |
| Beta | 92 | 2999,82 | 2957 | 13.5556 | H-COC stretch, cyclic ether, furthest from alkyne |
| Beta | 91 | 2931.72 | 3032 | 35.4397 | H-COC stretch, cyclic ether, closest to alkyne |
The IR results do vary a little. Surprisingly, the alkyne stretch of the beta anomer matches more closely the literature value for the alpha anomer. A possoble way of distinguishing the isomers could be by the cyclic ether C-H stretches since one is lower than the other and which is lower depends on the isomer according to the results of the calculation. However I think that as an analytical means of conclusively characterising one isomer with respect to the other, the results are not sufficient since IR stretches can have too large a fluctuation to afford reliability in this example.
References
- ↑ A. Kumar and S. S. Pawar, Journal of Molecular Catalysis A: Chemical, 2004,208,33-37.DOI:10.1016/S1381-1169(03)00510-7
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004 , DOI:10.1016/j.tetasy.2004.11.004
- ↑ A. S. Vieira, P. F. Fiorante, T. L. S. Hough, F. P. Ferreira, Lu, #x308, D. S. dtke, H. Stefani, #x301 and l. A., Org. Lett., 2008.DOI:10.1021/ol8022177
- ↑ A. S. Vieira, P. F. Fiorante, T. L. S. Hough, F. P. Ferreira, Lu, #x308, D. S. dtke, H. Stefani, #x301 and l. A., Org. Lett., 2008.DOI:10.1021/ol8022177
