Rep:Mod:scm4918
NH3 molecule
Molecule Information
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -56.55776873 a.u.
RMS gradient: 0.00000485 a.u.
Point group: C3v
N-H bond distance = 1.01798 Å
H-N-H bond angle = 105.74115 °
Optimisation
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Ammonia Molecule |
The optimisation file is liked to here
Frequancy Analysis
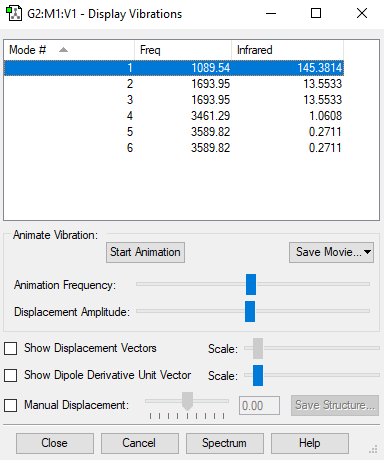
| symmetry | A1 | E | E | A1 | E | E |
|---|---|---|---|---|---|---|
| wavenumber /cm-1 | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| intensity /arbitrary units | 145 | 14 | 14 | 1 | 0 | 0 |
| image | 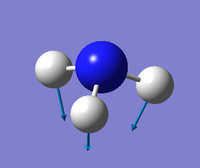
|
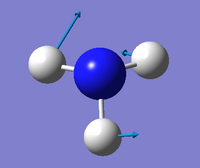
|
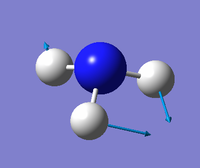
|
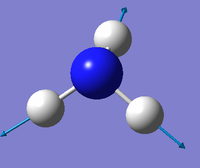
|

|
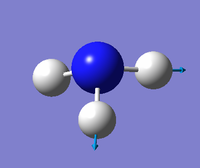
|
From the 3N-6 rule for non-linear molecules we would expect this molecule to have 6 modes. The two modes at wavenumber 1694 cm-1 and the ones at 3590 cm-1 are degenerate. The first three modes in the table are bending vibrations, the last three are bond stretching vibrations. The "umbrella" mode is the first one in the table at 1090 cm-1. In an experimental spectrum of gaseous ammonia you would expect to see 3 bands.
Atomic Charges
The charge on the N-atom was found to be -1.125 and 0.375 on the H-atom. This matches the expectation since Nitrogen is a more electronegative atom than Hydrogen and therefore draws electron density towards itself resulting in a relative negative charge. On each Hydrogen atom you would expect a third of the charge on the Nitrogen since there are three atoms all donating the same amount of electron density.
N2 molecule
Molecule Information
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: D∞h
N-N bond distance = 1.10550 Å
N-N bond angle = 180 °
Optimisation
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Nitrogen Molecule |
The optimisation file is liked to here
Frequancy Analysis
| symmetry | SGG |
|---|---|
| wavenumber /cm-1 | 2457 |
| intensity /arbitrary units | 0 |
| image | 
|
From the 3N-5 rule for linear molecules we would expect this molecule to have 1 mode. The mode shown in the table is a stretching vibration. In an experimental spectrum of gaseous nitrogen you would expect to see zero bands since the single stretching vibration does not produce a change in dipole moment.
Atomic Charges
There is no charge on either N-atom. This matches the expectation since they both have the same electronegativity and therefore the charge is equally distributed throughout the molecule.
H2 molecule
Molecule Information
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -1.17853936 a.u.
RMS gradient: 0.00000017 a.u.
Point group: D∞h
H-H bond distance = 0.74279 Å
H-H bond angle = 180 °
Optimisation
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Hydrogen Molecule |
The optimisation file is liked to here
Frequancy Analysis
| symmetry | SGG |
|---|---|
| wavenumber /cm-1 | 4466 |
| intensity /arbitrary units | 0 |
| image | 
|
From the 3N-5 rule for linear molecules we would expect this molecule to have 1 mode. The mode shown in the table is a stretching vibration. In an experimental spectrum of gaseous hydrogen you would expect to see zero bands since the single stretching vibration does not produce a change in dipole moment.
Atomic Charges
There is no charge on either H-atom. This matches the expectation since they both have the same electronegativity and therefore the charge is equally distributed throughout the molecule.
Structure and Reactivity
Mono-metallic TM Complex
A search for mono-metallic TM complexes that coordinate H2 was ran in ConQuest software. The H-H bond length was defined as an identifier and one of the resulting molecules was selected. The unique identifier for the complex is: [HIHVIE] and the obtained H-H bond length=1.050Å. This is bigger than the value previously computed: H-H bond length=0.74279Å. This difference could arise from the fact that The 2 electrons in the H2 bond must be diffused between 3 atoms and therefore lead to a weaker, more dispersed bond. Another reason is that there are 6 ligands bound to the central metal complex. Therefore, one would expect an octahedral structure that requires a greater H-Ru-H angle and therefore pull the H-H bond further apart. However, the angles deviated from the regular octahedral ones since the 6 ligands are different and some much bigger than the H-atoms. These bigger ligands would have a repulsive effect on the H-H bond and reduce it. The rigidity of the H-H bond would also prvent it from reaching a 90° H-Ru-H angle that is expected from a octahedral complex.
Haber-Bosch process
E(NH3) = -56.5577687 a.u.
2*E(NH3) = -113.1155375 a.u.
E(N2) = -109.5241287 a.u.
E(H2) = -1.1785394 a.u.
3*E(H2) = -3.5356181 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)] = -146.5 kJ/mol
From this result we can conclude that the ammonia product is more stable.
CO molecule
Choice Molecule
Molecule Information
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -113.30945314 a.u.
RMS gradient: 0.00000433 a.u.
Point group: D∞v
C-O bond distance = 1.13794 Å
C-O bond angle = 180 °
Optimisation
Item Value Threshold Converged? Maximum Force 0.000007 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000004 0.001200 YES
Carbon Monoxide Molecule |
The optimisation file is liked to here
Frequancy Analysis

| symmetry | SG |
|---|---|
| wavenumber /cm-1 | 2209 |
| intensity /arbitrary units | 68 |
| image | 
|
From the 3N-5 rule for linear molecules we would expect this molecule to have 1 mode. The mode shown in the table is a stretching vibration. In an experimental spectrum of carbon monoxide you would expect to see one band since the single stretching vibration produces a change in dipole moment.
Atomic Charges
The charge on the O-atom was found to be -0.506 and 0.506 on the C-atom. This matches the expectation since Oxygen is a more electronegative atom than Carbon and therefore draws electron density towards itself resulting in a relative negative charge.
Molecular Orbitals
| MO number | 4 | 5 | 7 | 8 | 10 |
|---|---|---|---|---|---|
| energy /a.u. | -0.57004 | -0.46742 | -0.37145 | -0.02178 | 0.26241 |
| image | 
|

|
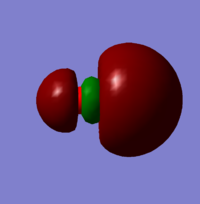
|
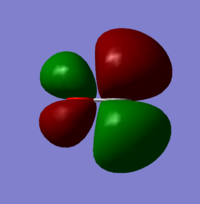
|

|
The 4th MO arises from the antibonding overlap of the 2sAOs. The 5th MO arises from the bonding overlap of two pAOs oriented perpendicular to the bond. The 7th MO arises from the bonding overlap of two pAOs oriented along the bond, this is the HOMO. The 8th MO arises from the antibonding overlap of two pAOs oriented perpendicular to the bond, this is the LUMO. The 10th MO arises from the antibonding overlap of two pAOs oriented along the bond (this orbital is also unoccupied).
A good reason for this molecules stability is the fact that only the bonding pAO based MOs are occupied.
P4 molecule
Extra Molecule
Molecule Information
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -1365.44182877 a.u.
RMS gradient: 0.00002517 a.u.
Point group: Td
P-P bond distance = 2.21771 Å
P-P-P bond angle = 60°
Optimisation
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000016 0.000300 YES Maximum Displacement 0.000101 0.001800 YES RMS Displacement 0.000076 0.001200 YES
White Phosphorus Molecule |
The optimisation file is liked to here
Frequancy Analysis
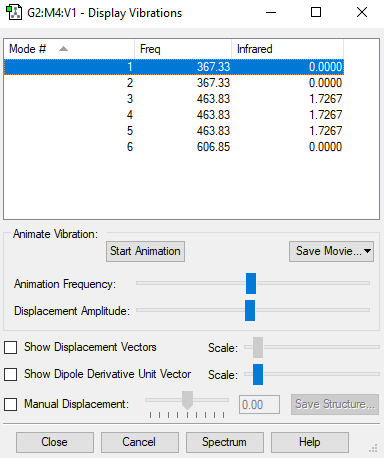
| symmetry | E | E | T2 | T2 | T2 | A1 |
|---|---|---|---|---|---|---|
| wavenumber /cm-1 | 367 | 367 | 464 | 464 | 464 | 607 |
| intensity /arbitrary units | 0 | 0 | 2 | 2 | 2 | 0 |
| image | 
|
|
|

|

|
|
From the 3N-6 rule for non-linear molecules we would expect this molecule to have 6 modes. The three modes at wavenumber 367 cm-1 and the three at 464 cm-1 are degenerate. In an experimental spectrum white phosphorous you would expect to see 1 band since the three IR-active vibrations are degenerate.
Atomic Charges
There is no charge on any P-atom. This matches the expectation since they all have the same electronegativity and therefore the charge is equally distributed throughout the molecule.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 0.5/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES, you have included too many d.p. though, for this method you should report angles to the nearest degree and bond lengths in A to 2 d.p.
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES, most answers are correct. However there are only 2 visible peaks in the spectra of NH3, due to the low intensity of the other 2 peaks. (See infrared column in vibrations table.)
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, However you have given a bond angle of 180 for N2 and H2, there are no bond angles in diatomic molecules. Bond angles involve exactly 3 atoms.
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 3/5
Have you completed the calculation and included all relevant information?
YES, you did include a bond angle which is invalid though.
Have you added information about MOs and charges on atoms?
YES, Your explanations are very good but the MO section is a bit short. More details would have increased your mark. The sentence on the molecule's stability is excellent well done!
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
You calculated P4, well done!
Do some deeper analysis on your results so far
