Structure Optimization

BH₃ Optimization

BH₃ 3-21G optimization: media:BH3 OPT 3-21G.LOG

The planar BH₃ molecule was constructed in gaussview. The bond length of the B-H bond in BH₃ was then altered to 1.5 Å and the molecule was then optimized using a 3-21G basis set using a B3LYP method.

A Gaussview image of the optimised BH₃ molecule.

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FOPT
Calculation Method:	RB3LYP
Basis Set:	3-21G
Final Energy (au):	-26.46226338
Gradient (au):	0.00020672
Dipole Moment (D):	0
Point Group:	D_3H
Calculation Time:	59 seconds
Bond Length (Å):	1.193
Bond Angle:	120^o

Convergence verification:

    Item               Value     Threshold  Converged?
 Maximum Force            0.000413     0.000450     YES
 RMS     Force            0.000271     0.000300     YES
 Maximum Displacement     0.001610     0.001800     YES
 RMS     Displacement     0.001054     0.001200     YES
 Predicted change in Energy=-1.071764D-06
 Optimization completed.
    -- Stationary point found.

Higher level basis set optimization

The molecule was then optimized with a higher level basis set, 6-31G(d,p) as to provide a more accurate representation of the structure of the compound.

BH₃ 6-21G(d,p) optimization: media:BH3 OPT 6-31G D P.LOG

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FOPT
Calculation Method:	RB3LYP
Basis Set:	6-31G(d,p)
Final Energy (au):	-26.61532363
Gradient (au):	0.00000235
Dipole Moment (D):	0
Point Group	D_3H
Calculation Time	27 seconds
Bond Length (Angstroms):	1.192
Bond Angle:	120^o

Convergence verification:

  Item               Value     Threshold  Converged?
 Maximum Force            0.000005     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000019     0.001800     YES
 RMS     Displacement     0.000012     0.001200     YES
 Predicted change in Energy=-1.304899D-10
 Optimization completed.
    -- Stationary point found.

Energy difference between the two optimizations: -0.1530602 au or equally, -401.86 kJ mol^-1

GaBr₃ Optimization

In order to optimize a molecule containing heavier atoms, a calculation that involves pseudo-potentials was accomodated, LANL2DP. In heavier atoms, we can treat the repulsive forces arising from the core orbital electrons as a background potential, rather than moving-interacting particles. This allows the calculation to employ several of the relativistic features that the electrons show in heavier atoms without sacrificing much computational time.

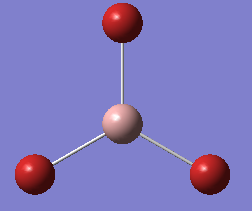
GaBr₃ LANL2DZ optimization: DOI:10042/25201

Log file: media:SC GaBr3 opt LANL2DZ.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FOPT
Calculation Method:	RB3LYP
Basis Set:	LANL2DZ
Final Energy (au):	-41.70082783
Gradient (au):	0.00000016
Dipole Moment (D):	0
Point Group	D_3H
Calculation Time	27.7 seconds
Bond Length (Å):	2.350
Bond Angle:	120^o

Convergence verification:

Item               Value     Threshold  Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000003     0.001800     YES
RMS     Displacement     0.000002     0.001200     YES
Predicted change in Energy=-1.282679D-12
Optimization completed.
-- Stationary point found.

Literature comparison:

Literature data
Ga-Br Bond length	Br-Ga-Br Bond angle
2.239 ± 0.007	119.1 ± 0.1

As it can be seen in the table above, the literature^[1] suggests a value which differs by 0.111 Å than the computed value (2.35018 ± 0.01 Å). Such error is not within the accuracy of this calculation and perhaps a more sophisticated approximation that exceeds the Pseudo potential approximation must be incorporated.

BBr₃ Optimization

For BBr₃ which contains both heavy and light atoms, a generic basis set was used, GEN, which allows the use of different basis sets for different molecules. This allows us to use the PP approximation for the Br atoms, for which it applies well but not use it for the B atom for which it does not apply as properly. A 6.31g(d,p) basis set was used for the B atom in this molecule whereas a LANL2DZ basis set was used for the Br atoms.

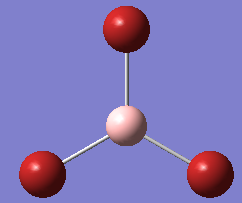
BBr₃ GEN optimization: DOI:10042/25216

Log file: media:SC BBr3 opt GEN.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FOPT
Calculation Method:	RB3LYP
Basis Set:	GEN
Final Energy (au):	-64.43645296
Gradient (au):	0.00000382
Dipole Moment (D):	0
Point Group:	D_3H
Calculation Time:	32.7 seconds
Bond Length (Angstroms):	1.93396
Bond Angle:	119.99^o

Convergence Verification:

Item               Value     Threshold  Converged?
Maximum Force            0.000008     0.000450     YES
RMS     Force            0.000005     0.000300     YES
Maximum Displacement     0.000036     0.001800     YES
RMS     Displacement     0.000023     0.001200     YES
Predicted change in Energy=-4.027604D-10
Optimization completed.
-- Stationary point found.

Structure Comparison

In covalent chemical bonds the bond length is dependent upon both the atomic orbital size of the participating atoms as well as the orbital overlap which takes place. As one would expect, the larger the valence orbitals participating in bonding the larger the length of the bond formed. In order to draw comparisons between the bonding of this compounds it is more wise to consider how the bond lengths of the computed compounds differ from a purely covalent model. Such analysis will aid one to reveal other factors are in play and how they contribute in the overall bonding of the molecule.

Structural properties table
Compound	Computed bond Length (Å)	Predicted bond length (Å)
BH₃:	1.192	1.15 Å
BBr₃:	1.933	2.04 Å
GaBr₃:	2.350	2.42 Å

Discussion:

In the case of BH₃ the bond length computed in this study is in good agreement with the predicted value^[2] based on covalent radii data.

Upon changing the ligand to Br, despite both H and Br being X ligands donating one electron to the metal centre, deviations can be seen in the case of BBr₃. In particular, the bond length of the B-Br bond is smaller than what would be predicted if the covalent radius of Boron and Bromine were added. This is mainly contributed to two reasons; The first one has to do with the larger difference in electronegativity between B and Br than that of B and H. These additional attractive electrostatic forces, also known as ionic contributions, contribute to the overall bond strength and hence equilibrium distance of the two atoms is smaller than what a completely covalent model would predict. The other factor that governs this bond shortening is the donation of the Bromine's lone pair to the vacant p orbital of the Boron atom. This p ↔ p orbital overlap offers additional stabilization energy to the B-Br bond, making the bond stronger and thus making the bond length shorter than predicted.

By changing the metal centre from Boron to Gallium, the valence orbitals become larger and more diffuse. As a consequence the orbital overlap between the metal and ligand is weaker and thus the bond strength also becomes weaker. Furthermore, Gallium is less electropositive than Boron and hence the ionic contributions are not as prevalent as in the case of BBr₃. As a consequence, the effects that contributed to the bond shortening of B-Br are not as pronounced in the case of Ga-Br and hence the computed value is closer to the completely covalent model.

Definition of a bond:

A bond is the equilibrium description of the sum of all electrostatic and exchange interactions present between the nuclei and electrons of different atoms, often found in close proximity to one another. The former is the sum of all coulombic interactions, attractive and repulsive exerted by the nuclei and electrons present. The exchange interaction on the other hand is non-classical. When in close proximity to another atom, the electrons present are in a superposition state which allows them to be partly localized in the nucleus of the other atom(s) that are in close proximity. This spreading of the electron to both nuclei increases the binding energy it feels (or equally reduces its kinetic energy) and hence electron density is built up between the centres of the nuclei present.

Gaussview uses a database that includes common bond lengths that are often seen in known compounds. If the distance is equal or smaller, it draws a bond betwen the two atoms. However, there could be significant attractions between two atoms that lead to a stable equilbrium at a distance greater than what the database Gaussview uses. As a consequence a bond won't be drawn between the two atoms.

Frequency analysis of optimized structures

BH₃

A frequency analysis was carried out on the optimized BH₃ structure which allows one to verify whether the optimized structure has reached a minimun in the potential energy surface. Both the method and basis sets used were the same as the optimization performed in order to ensure compatibility of the methods. A different method for instance might use approximations that would give erroneous results when used on a structure optimized with different approximations assumed.

Log file: media:BH3 FREQUENCY.LOG

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FREQ
Calculation Method:	RB3LYP
Basis Set:	6-31G(d,p)
Final Energy (au):	-26.61532363
Gradient (au):	0.00000237
Dipole Moment (D):	0
Point Group	D_3H
Calculation Time	9 seconds

Low Frequencies:

 Low frequencies ---   -0.9033   -0.7343   -0.0054    6.7375   12.2491   12.2824
 Low frequencies --- 1163.0003 1213.1853 1213.1880

As one can see all external degrees of freedom are within a small range indicating a good optimized structure. Furthemore no imaginary frequencies were present, hence the structure optimized did not fall into a metastable state.

Vibrational analysis table
no.	Form of the vibration	Frequency (cm^-1)	Intensity	symmetry D_3H point roup
1	In-phase movement of all Hydrogen atoms oscillating out of the plane of the molecule. The Boron atom moves in an out of phase manner with respect to the Hydrogen atoms.	1163	93	A₂"
2	The two Hydrogen atoms oscillate in a scissoring in-phase motion whereas the third hydrogen remains stationary.	1213	14	E'
3	The three Hydrogen atoms oscillate in an assymetric bending manner..	1213	14	E'
4	All hydrogen atoms oscillate in an in-phase manner in the plane of the molecule with the Boron atom being stationary.	2582	0	A₁'
5	Out of phase oscillation of two Hydrogen atoms in the plane of the molecule, with the third hydrogen atom being stationary.	2715	126	E'
6	In phase oscillation of two Hydrogen atoms in the plane of the molecule with the third one oscillating in out of phase, with respect to the other two.	2715	126	E'

The Infrared spectrum of BH₃

While the molecule has 6 vibrational modes, only three peaks appear in the Infrared spectrum. In order to interpret that one has to take into account the degenerate representations present in the point group, but also the selection rules that govern the coupling of electromagnetic radiation and electrons.

In particular, there are two sets of degenerate vibrations overlapping at the same frequency (1213.19 cm^-1 and 2715.43 cm^-1) and hence only one peak is seen in the spectrum.

Furthermore, the a₁' vibration, is totally symmetric and hence has a 0 transition dipole moment. As a consequence it will not interact with the electromagnetic wave and will be of zero intensity. Therefore 3 vibrations won't show up in the IR spectrum, leading to only 3 peaks being observed.

GaBr₃

A frequency analysis was carried out for GaBr₃ as to ensure that optimized structure is a minimun. The same method and basis sets were used as to ensure that the molecule stayed in an energy minimun.

GaBr₃ frequency analysis: DOI:10042/25232

Log file: media:SC GaBr3 freq 6 31G dp.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FREQ
Calculation Method:	RB3LYP
Basis Set:	LANL2DZ
Final Energy (au):	-41.70082783
Gradient (au):	0.00000011
Dipole Moment (D):	0
Point Group	D_3H
Calculation Time	13.9 seconds

Vibrational analysis table
no.	Form of the vibration	Frequency (cm^-1)	Intensity	symmetry D_3H point roup
1	The three Bromine atoms oscillate in an assymetric bending manner.	76	3	E'
2	The two Bromine atoms oscillate in a scissoring in-phase motion whereas the Gallium atom and the third Bromine oscillate a concerted manner in an out of phase manner with respect to the first two Bromine atoms.	76	3	E'
3	In-phase movement of all Bromine atoms oscillating out of the plane of the molecule. The Gallium atom moves in an out of phase manner with respect to the Bromine atoms.	100	9	A₂"
4	All Bromine atoms oscillate in an in-phase manner in the plane of the molecule with the Gallium atom being stationary.	197	0	A₁'
5	Assymetric streching of the two Ga-Br bonds with the third Bromine being stationary. The gallium atom's oscillation has a larger amplitude then the Bromine atom's.	316	57	E'
6	Oscillation of one Ga-Br bond with the two other Bromine atoms being stationary.	316	57	E'

Low Frequencies:

Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2010
Low frequencies ---   76.3744   76.3753   99.6982

There are two lowest 'real' normal modes, the degenerate E' pair which can be seen as a peak at 76 cm^-1 in the IR spectrum..

The Infrared spectrum of GaBr₃

Again, 6 vibrational modes exist but only three peaks appear in the Infrared spectrum. Since both GaBr₃ and BH₃ are in the same point group, the same principles used earlier to interpret the IR spectrum of BH₃ apply here as well.

There are two sets of degenerate vibrations which overlap at the same frequency (76 cm^-1 and 316 cm^-1) and hence only one peak is seen in the spectrum.

Similarly to BH₃, the a₁' vibration, is totally symmetric and hence has a 0 transition dipole moment. As a consequence it will not interact with the electromagnetic wave and will be of zero intensity. Therefore 3 vibrations won't show up in the IR spectrum, leading to only 3 peaks being observed.

Vibrational Comparison of BH₃ and GaBr₃

Table containing the frequencies of the corresponding D_3H vibrational modes:
BH₃ Frequencies (cm^-1)	GaBr₃ Frequencies (cm^-1)
1163 (a₂"	76 (e')
1213 (e')	76 (e')
1213 (e')	100 (a₂")
2582 (a₁'	197 a₁'
2715 (e')	316 (e')
2715 (e')	316 (e')

The Infrared spectra of the two compounds both show three peaks. There are two low frequency peaks (a₂" and e') of similar wavenumbers corresponding to the bending modes of the molecules and one high frequency peak e' corresponding to the stretching mode of the two compounds. As stated earlier the a₁' stretching mode occurs with zero transition dipole moment and hence is of zero intensity (IR inactive). The stretching modes are seen in much higher wavenumber frequency as the compression of a bond leads to high Pauli repulsions between the electrons of the two atoms sharing said bond. This is not the case with the bending modes as the bond length stays essentially invariant and the atoms do not approach eachother as much as to exert strong Pauli repulsions.

In order to understand the large difference in the wavenumber frequencies between BH₃ and GaBr₃ vibrations, one has to consider which parameters govern said frequencies. In the harmonic oscillator model, the wavenumber frequency is given by $v = \frac{1}{2 π} \sqrt{\frac{k}{μ}}$ where k is the force constant of the chemical bond and μ is the reduced mass.
As one would expect, the reduced mass of BH₃ is much smaller than that of GaBr₃ and hence we would expect the BH₃ frequencies to appear in higher wavenumbers. However if we were to assume that the force constant of the two compounds was approximately equal, we still wouldn't expect the frequencies for the former to appear at such low frequencies when compared to the latter. Since the wavenumber frequencies are significantly higher than what would be expected for similar force constants, the bonding in BBr₃ is stronger than in GaBr₃.

This difference in strength is attributed to the larger difference in electronegativity between B and Br, with respect to Ga and Br, the strength of the orbital overlap and the p-p overlap of the ligand and metal atoms. The first factor leads to increased ionic contributions present owed to the increased electrostatic attractions between the atoms. The second factor has to do with the interacting orbitals present; In the case of Ga, the orbitals donated to form the sigma framework are more diffuse than that of B and hence a weaker orbital overlap is produced between the metal centre and the ligand. Finally, the p↔p stabilization mentioned above is weaker in the case of Ga-Br as there is less π donation from the ligand orbitals as its p orbital is more diffuse than that of B. Overally these factors lead to a weaker metal-bromide bond and hence lower vibrational frequencies.

Another noticeable feature is the energy reordering of the vibrational modes of those two D_3H compounds. In particular, for GaBr₃ the a₂" vibrational mode is no longer the lowest energy mode, as was the case for BH₃. This is attributed to the quantum mechanical mixing of the e' vibrational states, an effect also known as Fermi Resonance. In general, significant mixing occurs between wavefunctions of the same point group and of similar energy. Whereas in BH₃ the energy difference between the two e' pairs was in the order of 1000 cm^-1, for GaBr₃ it is merely around 200 cm^-1. As a consequence significant mixing occurs and one pair of e' vibrations goes down in energy while the other goes up, resulting to an inversion of energy levels between the a₂" and e' vibrational modes.

Evidence in this claim is backed up by the fact that in the first pair of e' vibrations for GaBr₃, vibration no.1 as indicated in the table shows the Ga atom to oscillate in a motion thats perpendicular to the bending modes of the Br atoms. In BH₃ the B atom was stationary. Similarly in the scissoring vibration no.2, the third Br atom has a small oscillation amplitude something not seen in the case of BH₃ where only the two Hydrogen atoms oscillate with the third being stationary. This is effectively evidence of a coupled oscillation where the first pair of e' vibrational modes, due to quantum mechanical mixing, shows properties of the second e' pair.

The same basis set and method must be carried out for both optimisation and frequency calculations as the calculations follow similar ansatz and hence the frequency analysis will be heavily depended on the structure obtained through the optimization method. For instance the approximations assumed by one method might not be compatible with that of the other and thus this might lead to erroneous results.

The low frequencies represent the external degrees of freedom of the molecule, i.e the three translational motions (one in each cartesian dimension) and the three rotational motions (one axis along each cartesian dimension) of the whole molecule.

Molecular Orbitals

Population analysis of BH₃

A population analysis of BH₃ was carried out as to draw a comparison between the real orbitals and the qualitative LCAO theory.

BH₃ 6-31G(d,p) population analysis: media:BH3 pop analysis 631G d p.log

Dspace link: DOI:10042/25257

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	SP
Calculation Method:	RB3LYP
Basis Set:	6.31G(d,p)
Final Energy (au):	-26.61532363
Gradient (au):	--
Dipole Moment (D):	0
Point Group	D_3H
Calculation Time	15 seconds

Molecular orbital diagram and correlation with computed MOs:

As one can tell, the real molecular orbitals and the ones obtained via MO theory show the same features and ordering. This accuracy of MO theory makes it extremely useful for qualitative analysis. However, while for simple molecules such as BH₃ MO theory is really accurate, for more complicated compounds it fails to describe the unoccupied orbitals properly. As a consequence, more complex models are generally adopted in favour of the LCAO method.

NBO Analysis of NH₃

NH₃ Optimization

The NH₃ molecule was optimized using a B3LYP method and 6.31G(d,p) basis sets. A no symmetry command was accomodated as to allow for better optimization of the molecule.

NH₃ 6-31G(d,p) optimization: DOI:10042/25262

Log file: media:SC NH3 opt 631G d p.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FOPT
Calculation Method:	RB3LYP
Basis Set:	6.31G(d,p)
Final Energy (au):	-56.55776856
Gradient (au):	0.00000885
Dipole Moment (D):	1.8464 D
Point Group	C₁
Calculation Time	38.1 seconds

Convergence test:

Item               Value     Threshold  Converged?
Maximum Force            0.000024     0.000450     YES
RMS     Force            0.000012     0.000300     YES
Maximum Displacement     0.000079     0.001800     YES
RMS     Displacement     0.000053     0.001200     YES
Predicted change in Energy=-1.629715D-09
Optimization completed.
-- Stationary point found.

Frequency Analysis of NH₃

A frequency analysis was ran as to ensure that the optimized NH₃ molecule has a reached a minimun of the potential energy surface.

NH₃ Frequency analysis 6-31G(d,p): DOI:10042/25265

Log file: media:SC NH3 freq 631g d p.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FREQ
Calculation Method:	RB3LYP
Basis Set:	6.31G(d,p)
Final Energy (au):	-56.55776856
Gradient (au):	0.00000880
Dipole Moment (D):	1.8464 D
Point Group	C₁
Calculation Time	23.7 seconds

Low Frequencies:

Low frequencies ---  -30.8069   -0.0014   -0.0011    0.0009   20.2226   28.2150
Low frequencies --- 1089.5530 1694.1234 1694.1863

Vibrational analysis table
no.	Frequency (cm^-1)	Intensity	symmetry C_3V point group
1	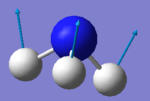1090	145	A₁
2	1694	14	E
3	1694	14	E
4	3461	1	A₁
5	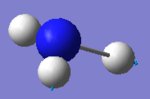3589	0	E
6	3589	0	E

Note: All computations were done using a C₁ point group to allow for better optimization of the molecule. However, the C_3V symmetry labels have been used to assign the vibrations. As a consequence of using the no symmetry point group, the E vibrational modes are not exactly degenerate but rather show deviations in the first decimal place.

Natural Bond Order analysis of NH₃

An NBO analysis of NH₃ was ran as to visualize the charge distribution of the NH₃ molecule. The method used was B3LYP with 6.31G(d,p) basis sets.

DSpace Link: DOI:10042/25269

Log file: media:SC NH3 pop analysis 631G d p.log

Results summary table
Summary	Results
File Type:	.chk
Calculation Type:	SP
Calculation Method:	RB3LYP
Basis Set:	6.31G(d,p)
Final Energy (au):	-56.55776856
Gradient (au):	0.00000000
Dipole Moment (D):	1.8464 D
Point Group	C₁
Calculation Time	-

NBO charge summary table
Atom	Charge
Nitrogen	-1.125
Hydrogen:	+0.375

Nitrogen is more electronegative than Hydrogen and as a consequence it withdraws electron density from the H atoms via the inductive effect. This results in a partially negative Nitrogen atom and three partially positive Hydrogen atoms. The sum of this charges however equals to 0, in accordance with a neutral charged molecule.

Reaction Energies

NH₃BH₃ Optimization

The structure of NH₃BH₃ was optimized using the same basis sets and method as for NH₃ and BH₃ as that will allow one to draw correlations between the energy of the three structures and hence the association energy of ammonia borane.

NH₃BH₃ optimization 6.31G(d,p): DOI:10042/25282

Log file: media:SC NH3BH3 opt 631G d p.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FOPT
Calculation Method:	RB3LYP
Basis Set:	6.31G(d,p)
Final Energy (au):	-83.22468897
Gradient (au):	0.00011154
Dipole Moment (D):	5.5664
Point Group	C₃
Calculation Time	1 minute, 25.7 seconds

Item               Value     Threshold  Converged?
 Maximum Force            0.000233     0.000450     YES
 RMS     Force            0.000083     0.000300     YES
 Maximum Displacement     0.000978     0.001800     YES
 RMS     Displacement     0.000369     0.001200     YES
 Predicted change in Energy=-4.037156D-07
 Optimization completed.
    -- Stationary point found.

Vibrational Analysis of NH₃BH₃

A frequency analysis was ran on the optimized structure of NH₃BH₃ as to ensure that the structure reached a minimun on the potential energy surface.

NH₃BH₃ Frequency analysis 6.31G(d,p):) DOI:10042/25283

Log file: media:SC NH3BH3 freq 631G d p.log

Results summary table
Summary	Results
File Type:	.LOG
Calculation Type:	FREQ
Calculation Method:	RB3LYP
Basis Set:	6.31G(d,p)
Final Energy (au):	-83.22468897
Gradient (au):	0.00011157
Dipole Moment (D):	5.5664
Point Group	C₃
Calculation Time	48.1 seconds

Low frequencies:

Low frequencies ---   -0.1566   -0.0574   -0.0117   14.8076   14.8893   42.0155
Low frequencies ---  265.6478  634.4597  639.6940

Associative energy determination

Overall energies
Molecule	Energy (au)
NH₃	-56.55776856
BH₃	-26.61532363
NH₃BH₃	-83.22468897

ΔE = E(NH₃BH₃) - E(BH₃) - E(NH₃)
Therefore, ΔE = -83.22468897 - (-56.55776856-26.61532363)
ΔE = -0.05159678 au

Equally, ΔE = -135.47 kJ mol^-1

Hence the dissociation energy is: E_dis= +135.47 kJ mol^-1

The bond's energy is in the right order of magnitude that one would expect from a strong covalent bond.

References

↑ B. Réffy, M. Kolonits, H. Magdolna, J. Mol. Struct., 1998, 445, 139–148.
↑ P. Atkins, T. Overton, J. Rourke, M. Weller, F. Armstrong, "Inorganic Chemistry", 5th Edition, 2010, Oxford University Press.

[one-1] B. Réffy, M. Kolonits, H. Magdolna, J. Mol. Struct., 1998, 445, 139–148.

[two-2] P. Atkins, T. Overton, J. Rourke, M. Weller, F. Armstrong, "Inorganic Chemistry", 5th Edition, 2010, Oxford University Press.

[1]

[2]

Structure Optimization

BH3 Optimization

Higher level basis set optimization

GaBr3 Optimization

BBr3 Optimization

Structure Comparison

Frequency analysis of optimized structures

BH3

GaBr3

Vibrational Comparison of BH3 and GaBr3

Molecular Orbitals

Population analysis of BH3

Molecular orbital diagram and correlation with computed MOs:

NBO Analysis of NH3

NH3 Optimization

Frequency Analysis of NH3

Natural Bond Order analysis of NH3

Reaction Energies

NH3BH3 Optimization

Vibrational Analysis of NH3BH3

Associative energy determination

References

BH₃ Optimization

GaBr₃ Optimization

BBr₃ Optimization

BH₃

GaBr₃

Vibrational Comparison of BH₃ and GaBr₃

Population analysis of BH₃

NBO Analysis of NH₃

NH₃ Optimization

Frequency Analysis of NH₃

Natural Bond Order analysis of NH₃

NH₃BH₃ Optimization

Vibrational Analysis of NH₃BH₃