Rep:Mod:sarasmolecules
AX3 Section
BH3
Method/Basis Set: B3LYP/6-31G(d,p)
Summary Table:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000064 0.001800 YES RMS Displacement 0.000039 0.001200 YES
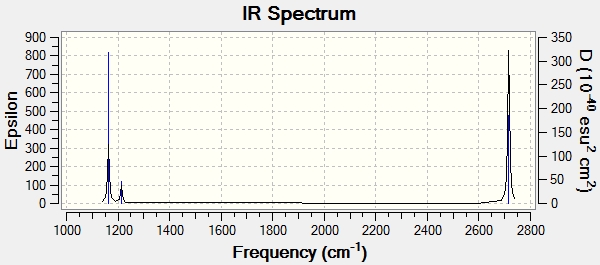
Frequency Analysis: BH3 log file
Low frequencies --- -7.5936 -1.5614 -0.0055 0.6514 6.9319 7.1055 Low frequencies --- 1162.9677 1213.1634 1213.1661
Frequency Calculated BH3 Molecule |
| Wavenumber (cm-1) | Intensity (a.u.) | Symmetry | IR active | Type | |
|---|---|---|---|---|---|
| 1 | 1163 | 93 | A2" | YES | Out-of-plane Bend |
| 2 | 1213 | 14 | E' | YES (slightly) | Bend |
| 3 | 1213 | 14 | E' | YES (slightly) | Bend |
| 4 | 2582 | 0 | A1' | NO | Symmetric Stretch |
| 5 | 2716 | 126 | E' | YES | Asymmetric Stretch |
| 6 | 2716 | 126 | E' | YES | Asymmetric Stretch |
There are 6 vibrations but only 3 peaks present in the IR spectrum; vibration 4 (see table above) is a symmetric stretch and so it is not IR active and does not show a peak on the spectrum. Also, vibrations 2 and 3 are degenerate and so are represented by a single peak on the spectrum, as are vibrations 5 and 6. Although vibrations 2 and 3 are IR active, their intensity is very low (14 a.u.) therefore the IR absorption peak is small.
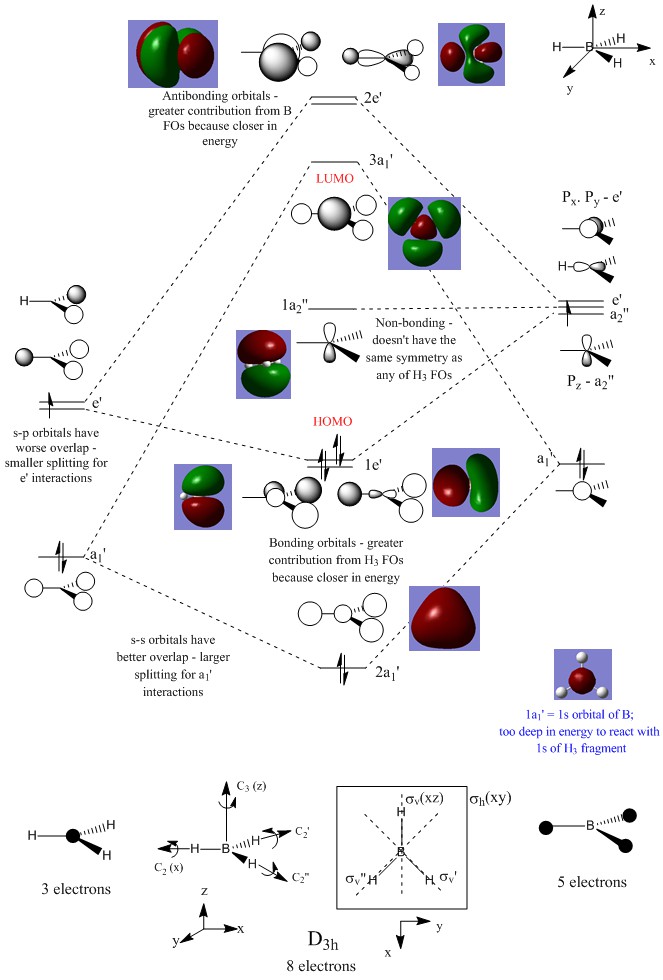
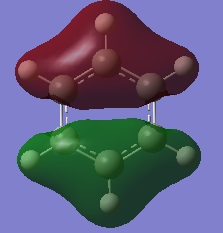
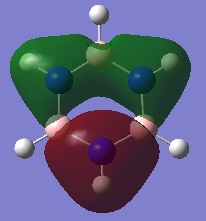
MO Diagram:
Ng611 (talk) 13:44, 21 May 2018 (BST) Very thorough and accurate MO analysis. Why is the 3a1 orbital the LUMO?
The LCAOs don't show how the MOs change shape after they overlap/interact, they just show the FOs (with their relative sizes) on the same skeleton, therefore their shapes are different to the real MOs shown. Qualitative MO theory is accurate enough for constructing a rough MO diagram and determining relative energies of FOs and MOs, however a quantitative calculation is required for an accurate picture of what the MOs actually look like and their energies. For example, the qualitative approach of MO theory fails when we are unable to determine ordering of MOs because we don't know the if the quality of orbital overlap (s-s>s-p>p-p>p-p pi etc.)is the dominant factor or if the difference of energy between reacting FOs is, therefore we need to use the quantitative approach for an accurate picture.
NH3
Method/Basis Set: B3LYP/6-31G(d,p)
Summary table:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Frequency Analysis: NH3 log file
Low frequencies --- -8.5646 -8.5588 -0.0041 0.0455 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
- exceeds +15cm-1 but everything is converged in log file, no need to rerun
Ng611 (talk) 13:46, 21 May 2018 (BST) Did you double check this with a demonstrator before continuing? If you did, you need to make a note of it in the wiki.
Frequency Calculated NH3 Molecule |
BH3-NH3
Method/Basis Set: B3LYP/6-31G(d,p)
Summary Table:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000123 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000515 0.001800 YES RMS Displacement 0.000296 0.001200 YES
Frequency Analysis: BH3-NH3 log file
Low frequencies --- -13.3839 0.0011 0.0012 0.0012 19.3842 43.0622 Low frequencies --- 266.2345 632.1413 638.2019
Frequency Calculated BH3-NH3 Molecule |
Association Energy:
- E(BH3) = -26.61532 a.u.
- E(NH3) = -56.55777 a.u.
- E(BH3-NH3) = -83.22469 a.u.
- ΔE=E(BH3-NH3)-[E(NH3)+E(BH3)] = [ -83.22469 - ( -22.61532 - 56.55777 ) ]a.u. = -0.0516 a.u. = -135 kJmol-1 +- 10kJmol-1
Ng611 (talk) 13:52, 21 May 2018 (BST) Good calculation. How does the strength of this bond compare to others?
BBr3
Method/Basis Set: B3LYP/6-31G(d,p)LANL2DZ
Summary Table:
*Point group not D3h - demonstrator said it is fine to continue with frequency calculation.
Item Table:
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000058 0.001800 YES RMS Displacement 0.000029 0.001200 YES
Frequency Analysis: DOI:10042/202375
Low frequencies --- -0.6133 0.0001 0.0002 0.0002 2.1102 5.7165 Low frequencies --- 155.9558 156.0185 267.7126
Frequency Calculated BBr3 Molecule |
Project Section - Aromaticity
Benzene
Method/Basis Set: B3LYP/6-31G(d,p)
Summary Table:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000194 0.000450 YES RMS Force 0.000077 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000289 0.001200 YES
Frequency Analysis: Benzene log file
Low frequencies --- -2.1456 -2.1456 -0.0089 -0.0043 -0.0042 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Frequency Calculated Benzene Molecule |
Borazine
Method/Basis Set: B3LYP/6-31G(d,p)
Summary Table:
Item Table:
Item Value Threshold Converged? Maximum Force 0.000112 0.000450 YES RMS Force 0.000046 0.000300 YES Maximum Displacement 0.000419 0.001800 YES RMS Displacement 0.000106 0.001200 YES
Frequency Analysis: Borazine log file
Low frequencies --- -6.0049 -5.7880 -5.2772 -0.0106 0.0586 0.1780 Low frequencies --- 289.2498 289.2578 403.8919
Frequency Calculated Borazine Molecule |
NBO Charge Analysis
| Benzene | Borazine |
|---|---|
 |
|
Ng611 (talk) 13:55, 21 May 2018 (BST) Good analysis. I would suggest tabulating the charges, as the charges of some of the hydrogens on Borazine are impossible to make out.
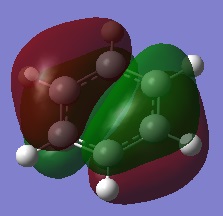
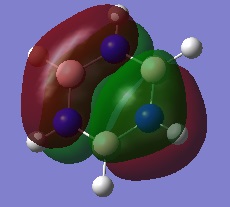
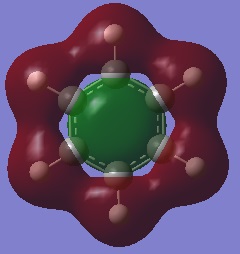
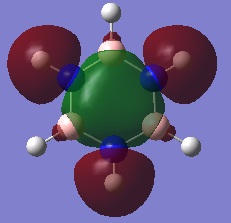
- The colours on each atom represent the charge distribution within each molecule, relative to each other. The lighter the green, the more positive the charge, the more red the more negative the charge and the dark (~black) show neutral charges/close to neutral.
- The diagram for benzene shows identical dark red carbon atoms and identical dark green hydrogen atoms; this means that the carbon-hydrogen bonds are very little polarised and so the carbon atoms have a very small (and identical) 𝛿- charge and the hydrogen atoms have a very small 𝛿+. This is because there is only a small electronegativity difference between carbon and hydrogen, so the charge distribution will not be significant in benzene and the atoms are almost neutral.
- On the other hand, in borazine there are B-H, N-H and B-N bonds to consider. Nitrogen is the most electronegative of the three atoms and it is bonded to two more electropositive atoms so it has the most bright red atom (image below shows borazine with atomic labels to differentiate between boron and nitrogen). The boron atom is the lightest of the green atoms because it is the least electronegative (most electropositive) atom and is bonded to two more electronegative atoms. The hydrogen atom in the N-H bonds is green but (dark) red in the B-H bonds because it is less electronegative than nitrogen but more than boron. However, the electronegativity difference between boron and hydrogen isn't very large therefore the hydrogen is a dark red, almost black/neutral.
- Overall, this shows that borazine has a greater charge distribution than benzene as it consists of atoms with different electronegativities and thus more polarised bonds.
Ng611 (talk) 13:57, 21 May 2018 (BST) Well explained, although I would also include a discussion of how the symmetry of the molecule affects the distribution of charges, as well as mentioning that the overall charge is 0.
Comparing Benzene and Borazine MOs
| Benzene | Borazine | Comparison |
|---|---|---|
 |
 |
MO 21 is the HOMO of both molecules. The MOs involve pi interactions, i.e. p-p side overlap thus these overlaps on adjacent carbons or boron/nitrogen atoms are not strong interactions, despite being short range (due to diffuse nature of p orbitals leading to weak overlap). Although they are overall anti-bonding MOs, they both have bonding character between the adjacent, in-phase p orbitals. They each have 2 perpendicular planar nodes. In the borazine MO, not all of the H atoms contribute to the MO and thus it is lower in energy because it has less anti-bonding character (has smaller lobes on one side) . The benzene MO is more symmetrical and resembles a d-orbital. |
 |
 |
MO 9 of benzene and borazine exhibit bonding and anti-bonding character. Overlap in both MOs are sigma overlaps therefore they are relatively strong interactions; in borazine there are s-p sigma overlaps whereas in the benzene MO there are only s-s sigma overlaps therefore the borazine MO is not symmetrical/doesn't have the same symmetry as benzenes MO. |
 |
 |
MO 12 of Benzene and MO 10 of Borazine - overall bonding orbitals. Borazine MO is lower in energy because it has less anti-bonding character - 3 of the H atoms (bonded to Nitrogen) have no contributions therefore there is less out-of-phase overlap. Both MOs are symmetric but benzenes MO is more symmetric i.e. has a C6 principle axis whereas borazine MO has a C3 axis. Both MOs are due to sigma overlap; p orbitals of C or B overlapping with H 1s orbitals - medium strength interaction. Also, although the benzene MO is higher in E, there is in-phase s-s overlap between the H atoms however these are not too strong as they are overlapping through space. |
Aromaticity
Aromatic compounds, such as benzene and borazine, exhibit unusual properties; for example they are more stable than their corresponding non-aromatic compounds, they undergo substitution reactions instead of addition and they have shorter bonds. Historically, it was commonly said that what makes them aromatic is their delocalised pi-system, commonly described as the overlap of adjacent pz orbitals; although this is not incorrect, it is not the whole picture.
For a cyclic-compound to be aromatic, it must obey the following rules:
- It must be planar.
- It must have p-orbitals perpendicular to the ring, which are continuous/in a cyclic array
- It must have 4n+2 pi electrons (Huckel's rule)
Therefore, describing an aromatic system only by 'the overlap of pz-orbitals' is not enough! For example, in cyclohex-1-ene, 2 of the carbon atoms have an overlap of two pz orbitals but:
- The molecule is not planar
- There is not an uninterrupted cyclic array of p-orbitals
Therefore it is not aromatic; the overlap of perpendicular p-orbitals occurs in non-aromatic substances too.
Furthermore, computed MOs describe aromaticity in the same way as they show electron clouds delocalised over more than one atom whereas LCAOs shows the AOs localised on one atom/between specific bonds.
Ng611 (talk) 14:02, 21 May 2018 (BST) What you've written certainly isn't incorrect, but more detail is needed. How has the conceptual picture of aromaticity changed with quantum mechanics? Is it simply pi delocalisation the drives aromaticity? How can aromaticity be confirmed via experiment?