Rep:Mod:saigou
Introduction
Normal 0 false false false EN-GB ZH-TW X-NONE
Cope Rearrangement
The Cope Rearrangement is a pericyclic [3,3]-sigmatropic rearrangement reaction which involves a simultaneous σ-bond breaking and forming in a concerted fashion as shown in Fig. 1.1.
After years of controversy, recent research has confirmed that the reaction undergoes a concerted mechanism with two possible geometries for its transition state: the chair or the boat conformation.
>>>
D) Different conformers are manually adjusted by altering the 3 main dihedral angles between the carbons, with the numbering of carbon atoms correspond to that as labelled in Fig.1.4. The dihedral angles listed below are the angles that were set before optimisation.
| Conformer | Corresponding to Appendix 1 | Dihedral Angle between C1 to C4 | Dihedral Angle between C2 to C5 | Dihedral Angle between C3 to C6 | Energy (a.u.) | Point Group | Output Link | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anti-conformer 1 |
|
anti 2 | 120o | 180o | 120o | -231.69253527 | Ci | Anti Conformer 1 | |||
| Anti-conformer 2 |
|
anti 3 | 0o | 180o | 0o | -231.68907050 | C2h | Anti Conformer 2 | |||
| Anti-conformer 3 |
|
anti 4 | 60o | 180o | 120o | -231.68937804 | C1 | Anti Conformer 3 | |||
| gauche-conformer 1 |
|
gauche 2 | 180o | 60o | 180o | -231.69166701 | C2 | Gauche Conformer 1 | |||
| gauche-conformer 2 |
|
gauche 3 | 120o | 60o | 180o | -231.69266110 | C1 | Gauche Conformer 2 | |||
| gauche-conformer 3 |
|
gauche 1 | 0o | 60o | 0o | -231.68771613 | C2 | Gauche Conformer 3 | |||
From the information above, it is surprise to discover that the lowest energy conformer is the ‘’Gauche 1’’ conformer (energy of -231.68771613 Hartree a.u.) instead of an ‘’anti’’ conformer as predicted. When considering the relative stability of a molecule, stereo-electronic factor is usually considered together with the sterics. Since the Gauche conformer is the most stabilised one, the favourable electronic interaction in this conformation overrides the strain arises from sterics.
To have a better understanding of the electronic interaction of ‘’Gauche 1’’ conformer, its frontier molecular orbitals were simulated from its checkpoint file and in particular the HOMO and LUMO of ’’Gauche 1’’ were pictured:
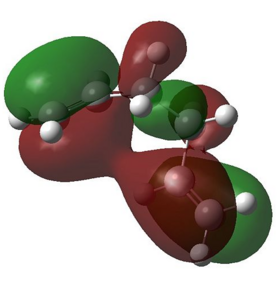
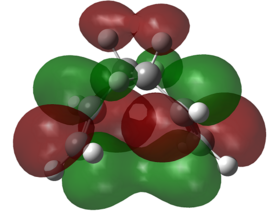
In the HOMO of ‘’Gauche 1’’ molecule, the two alkene bonds are orientated in such a way that the π cloud orbitals of both C=C bonds are in phase with each other, allowing favourable π- π interactions and therefore stabilised the molecule. Similar interactions can also be found in the LUMO, where the antibonding orbitals of both C=C*bonds are aligned in the correct orientation and allowed favourable orbital overlap between the two alkene groups, hence stabilising the molecule. This stabilising interaction cannot be found in anti-conformers as the two alkene groups are pointed away from each other, hindering the possibility of orbital overlap. These favourable orbital interactions in ‘’Gauche 1’’ conformer outweighed the destabilisation arose from sterics clashes and is the lowest energy conformer.
E) The required ‘’anti 2’’ conformer was optimised previously at HF/3-21G level as shown above with point group of Ci symmetry.
F) Another optimisation method with higher accuracy was applied to the anti-2 conformer with the following input:
Job type: optimisation
The method: DFT – B3LYP
The basis set: 6-31G
| Basis Set | Output Logfile | Point Group | Energy/ Hartree a.u. | Energy / Kcal mol-1 |
| ’’’HF/3-21G’’’ | [ HF/3-21G opt.] | C1 | -231.69254 | -608308.75 |
| ’’’DFT-B3YLP/6-31G’’’ | [DFT-B3LYP /6-31G opt.] | C1 | -234.55970 | -615836.48 |
| ’’’Energy Difference’’’ | - | - | -2.86716 | -7527.73 |
| ’’’Basis Set’’’ | ’’’Dihedral angle (C1-C4)/o’’’ | ’’’Dihedral angle(C2-C5)/o’’’ | ’’’Dihedral angle(C3-C6)/o’’’ | ’’’C=C bond length/Å’’’ | ’’’C2-C3/ C4-C5 bond length/ Å ‘’’ | ’’’C3-C4 bond length/ Å’’’ |
| ’’’HF/3-21G’’’ | 114.63 | 179.96 | 114.63 | 1.3162 | 1.5089 | 1.5530 |
| ’’’DFT-B3YLP/6-31G’’’ | 118.71 | 180.00 | 118.71 | 1.3383 | 1.5072 | 1.5550 |
E) Optimisation of anti 2 Conformer
The required anti 2 conformer was optimised previously in the initial optimisation for anti conformer at HF/3-21G level as shown above with point group of Ci symmetry.
F) Comparison between Optimisation at HF/3-21G and DFT-B3LYP/6-31G Level
DFT optimisation method is another optimisation method with higher accuracy and was applied to the anti 2 conformer with the following input:
Job type: optimisation
The method: DFT – B3LYP
The basis set: 6-31G
| Basis Set | Output Logfile | Jmol modelling | Point Group | Energy/ Hartree a.u. | Energy / Kcal mol-1 |
| HF/3-21G | HF/3-21G opt. | 'XML error: > required at line 5 | C1 | -231.69254 | -608308.75 |
| DFT-B3YLP/6-31G | DFT-B3LYP /6-31G opt. | ' | C1 | -234.55970 | -615836.48 |
| Energy Difference | - | - | -2.86716 | -7527.73 |
| Basis Set | Dihedral angle (C1-C4)/o | Dihedral angle(C2-C5)/o | Dihedral angle(C3-C6)/o | C=C bond length/Å | C2-C3/ C4-C5 bond length/ Å | C3-C4 bond length/ Å |
| HF/3-21G | 114.63 | 179.96 | 114.63 | 1.3162 | 1.5089 | 1.5530 |
| DFT-B3YLP/6-31G | 118.71 | 180.00 | 118.71 | 1.3383 | 1.5072 | 1.5550 |
From the 3D model, there is no visible difference between the two optimised anti-2 conformer. The physical data for both were compatible and has one noticeable deviation on the diherdral angle between C1-C4 and C3-C6. This value produced for optimising at HF/3-21G level is 114.63o whereas that for optimising at DFT-B£YLP/6-31G level is 118.71o. The C=C bond length of ~1.32 Å and C-C bond length of ~1.51 Å /1.55 Å are in good agreement with the literature[1] and therefore both optimisation method yields pretty accurate result for 1,5hexadiene molecule.
?????ENERGY DISCUSSION??????????
G) ????
[1] Gyorgy Schulte, Istvan Hargittai, J. Of Molecular Structure, 1995, Vol 346,63-69. DOI|10.1016/0022-2860(94)09007-C
