Rep:Mod:sadr3

Module 3

Sadia Rahman

Introduction

In this report transition states and reactivity will be looked. The characterisation of the transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions will be looked at. Molecular orbital based methods will be used and the Schrödinger equation will be solved numerically in the calculations. The locating of the transition structures are based on the local shape of a potential energy surface. The transition structures will be analysed and the reaction paths and barrier heights analysed. Most of the calculation will be ran on the laptop so any data collected will be added as LOG files and D-space links added as appropriate.

The Cope Rearrangement

Introduction

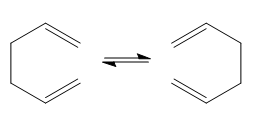
In the computational experiment for the Cope rearrangement the transition structure on a potential energy surface will be look at. The Cope rearrangement of 1,5-hexadiene will be looked at as shown below, it is a pericyclic reaction. It is a [3,3]-sigmatropic shift rearrangement. Its mechanism is a concerted one which goes via a "chair" or a "boat" transition structure, with the "boat" transition structure lying higher in energy. This will be analysed further below.

Optimising the Reactants and Products

The structures will be optimised and the symmetry groups looked at, to find the point group. The vibrational frequencies and potential energies looked at to compare to experimental values. Initially GaussView was used to draw the 1,5-hexadiene anti-linkage and the structure cleaned, then optimised with HF/3-21G level of theory. The anti-periplanar relationship was seen and the energy and point group was obtained from the summary and the symmetrize. Then the 1,5-hexadiene gauche-linkage was looked at and the structure cleaned. Then it was optimised with HF/3- 21G level of theory and the summary file and symmetrize looked at. The data found is summarised in the table below. The energy conversion used was 1 Hartree= 627.5095 kcal/mol. All the calculations types used were FOPT and method of RHF, and basis set of 3-21G. Only relevant data has been added from the summary below. The anti and gauche structures were then compared to: Appendix 1. It was found that them to be gauche 4 and anti 1

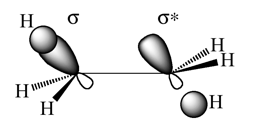
It would be expected that the gauche structure would be higher in energy due to more steric clashes. Also as the anti-periplanar conformers have a favourable interaction between the C-C/C-H σ-orbital and the C-C/C-H σ*-orbital as the orbital overlap is best for app rather than gauche as shown be the image below.

However it was found that the anti 1 was lower in energy than the gauche 4 due to having a smaller energy. It can be seen that the gauche conformer is 0.64 kcal/mol larger in energy than the anti conformer. This indicates that there is another factor other than sterics, which is effecting the stability of the conformers. This was considered by also looking at the highest anti and gauche conformer of anti 3 and the gauche 4 ( gauche 1 anti 3). The lowest energy conformer gauche 3 was also found by varying the dihedral angle as it was found to be 67.8 ⁰ and by making the overlap of the C=C less and maximising the vinyl C-H overlap greater, as this had a favourable interaction. An explanation for the gauche being higher was that the π orbitals interacted with the protons this can be seen easier if the Newman projection is considered.

There is a van der Waals attraction when the H..H distance is 2.4 Å and in gauche 4 it is 2.49 Å and this increases to 2.54 Å for gauche 1, as does the energy. The lowest conformer gauche 3 has the distance closest to this van der Waals attraction at 2.41 Å. The anti conformers has larger values for anti 1 at 2.51 Å for anti 3 2.50Å, this can be used to explain the relative stabilisation as this van der Waals attraction can help with stabilisation.

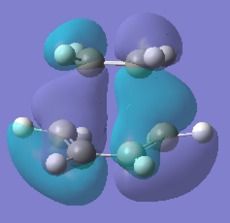
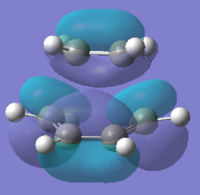
Also the gauche 3 is the most stable conformer this is due to the favourable donation of the π C=C orital into the neighbouring C-H σ*-orbitalwhich helps to stabilise it, this can also be seen from the MO diagram below. There is more of this present in gauche 3 than gauche 1 hence it is more stable. The orbitals are closer together so can have more interaction as can be seen from the van der Waals attraction distance. The high π orbital energy and low σ* energy gives rise to the favourable interaction and larger stability. Therefore the gauche conformation can be rationalised to be lower in energy than the antiperiplanar conformation.

Energy and point group's

	anti 1	anti 3	gauche 4	gauche 1
Jmol
Energy/ au	-231.69226	-231.68907	-231.69153	-231.68772
Energy/ kcal/mol	0.04	2.25	0.71	3.10
Point group	C2	C2h	C2	C1

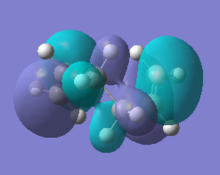
The MO of the conformers was looked to see if this could explain the difference in the energies, the HOMO was looked at. MO of highest and lowest anti and gauche conformers looked at, as the double bond was clearly having an influence on the relative energies. The lowest conformers were anti 1 and gauche 3 ( gauche 3) as the HOMO of gauche 3 is lower by (0.001 a.u) 0.63 kcal/mol, which indicated that the lower gauche conformer HOMO is lower in energy and more favourable. If the π orbitals are looked at then the gauche orbital is more diffuse and spread out through the molecule, across the double bonds. This is not as evident in anti 1 and this illustrates that the π-orbitals overlap effects the relative stability of the molecules. Overall the above showed that there were many factors playing a part in the relative stabilisation of the different conformers. The structure which were found match well to those refereed to in Appendix 1. The HOMO energies also do not correspond to the relatives energies of the conformers.

MO: HOMO orbitals

	anti 1	anti 3	gauche 3	gauche 1
MO (HOMO)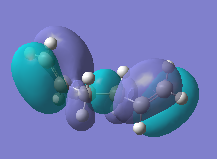
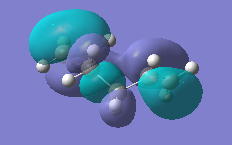MO energy (au)	-0.351	-0.358	-0.352	-0.347

Optimising C_i conformer with HF and DFT

The C_i conformer was then optimised with HF/3-21G and the final energy compared. The energy was -231.69253 Hartrees, which was very similar to the one computed in the appendix above, of -231.69254 Hartrees. This was then re-optimised with B3LYP/6-31G(d) using DFT method. The geometry stayed the same, and the angles, bond lengths and energies can be seen below. The energy difference cannot be compared as different methods were used. The methods were therefore compared by analysis of the geometries below. The DFT method produced different angle and length data to the HF method, the accuracy can be looked at by comparison to literature. The difference between the dihedral angles in larger then the bond lengths.

C_i conformer

	HF/3-21G	B3LYP/6-31G(d)
Jmol
Energy/ au	-231.69253	-234.61171
Point group / kcal/mol	Ci	Ci
	anti Ci- HF	anti Ci- DFT

Anti Ci numbering

The numbering can be seen above, the C=C is larger in DFT then HF and the C-C smaller by 0.01 Å in both cases. The literature is closer to the B3LYP/6-31G(d) which is the higher level basis set so has more accurate results.

C_i conformer bond lengths

Bond lenghts/Å	HF/3-21G	B3LYP/6-31G(d)	Literature
C1-C2	1.32	1.33	1.34
C2-C3	1.51	1.50	1.50
C3-C4	1.55	1.55	1.54
C4-C5	1.51	1.50	-
C5-C6	1.32	1.33	-

The dihedral angles were also looked at and the C₂-C₃-C₄-C₅ is closer to the optimal 180^o, the difference is only slightly. Overall it can be said that the DFT method has not changed in comparison to the HF method as the point group has been retained. The HF method often overestimates the total energy is optimisation, but in this section it can be thought to be sufficient as the geometries have not changed a great deal.

C_i conformer dihedral angle/^o

	HF/3-21G	B3LYP/6-31G(d)
C1-C2-C3-C4	114.6	118.6
C2-C3-C4-C5	179.8	180.0
C3-C4-C5-C6	-115.1	-118.6

To enable the comparison of the energies the frequency calculation was ran. The frequency calculation was carried out to characterise the critical point, it was confirmed that the a minimum ground structure was made as all frequencies are real and positive as can be seen by the IR below and the data shown below. The IR data could also be further analysed by added the corresponding peaks to the molecules vibrations.

This analysis allowed thermochemistry data to be looked at, which is shown below. This gives useful energy values as the energy found in Gaussview is an electronic energy term of the molecule at 0K, but the experimental data is recorded at room temperature, which the following does.

The following energies were noted: (i) the sum of electronic and zero-point energies (ii) the sum of electronic and thermal energies (iii) the sum of electronic and thermal enthalpies (iv) the sum of electronic and thermal free energies.

i) The potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE) ii)The energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans. iii) Same as ii, but there is an additional correction for RT (H = E + RT) included, this is important when looking at dissociation reactions. iv)The entropic contribution to the free energy (G = H - TS).

The same energies were also analysed for 0K by editing log file as follows. The Freq=ReadIsotopes option in Gaussian was added and the data below added:

0.001 1.0
12.0
1.0
1.0
12.0
1.0
12.0
1.0
1.0
12.0
1.0
1.0
12.0
1.0
12.0
1.0
1.0

The temperature was in putted as 0.001, so no errors would occur in GaussView. The data showed that there was no kinetic energy present as 0K as expected. There is only zero point energy present, so all the energy values were the same. The slight different in the sum of electronic and zero-point energies in 298.15 K and 0 K was probably due to the correction energy differing and the 298.15 K computation taking a more accurate atomic mass number, however the data was reran with FredChk . They were computed as being the same by specifying the scale as 1.

Electronic energy	298.15 K and 1 atm	0 K and 1 atm
Sum of electronic and zero-point energies	-234.469203	-234.469203
Sum of electronic and thermal free energies	-234.461857	-234.469203
Sum of electronic and thermal enthalpies	-234.460913	-234.469203
Sum of electronic and thermal free energies	-234.500776	-234.469203

Optimising the Chair and Boat Transition Structures

In this part the transition structure will be optimised by computing the force constants at the beginning of the calculation and then using the redundant coordinate editor and using the QST2. The reaction coordinate and the Intrinisic Reaction Coordinate (IRC) looked at so that the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures can be calculated.

Chair Transition Structure

Initially an allyl fragment (CH₂CHCH₂) was drawn and optimised using the HF/3-21G level of theory. The structure computed look like one half of the transition structures from Appendix 2. This was then copied twice into a new window and oriented so that they look roughly like the chair transition state. The distance between the terminal ends of the allyl fragments was ~ 2.2 Å apart. The transition state was then manually optimised in two different ways.

The first method used was optimising a transition state with a reasonable guess, by computing the force constants. The optimisation and frequency was ran with 'Opt+Freq' and the Optimisation changed from a minimum to TS (Berny), with the force constants calculated Once. The additional key words added was Opt=NoEigen, this stopped the computation stopping if more than one imaginary frequency is detected during optimisation. This should give an imaginary frequency of magnitude 818 cm^-1, this can be seen below. This corresponds to the Cope rearrangement, where a bond is being formed causing the molecules to come closer together, while the other has a greater distance between them, so bonds are being made and broken in the transition state.

The second optimisation was carried out by again taking the guess structure, and using the Redundant Coordinate Editor so that the coordinated were frozen and setting the terminal carbons to 2.2Å apart. Then the optimisation set up like it was a minimum and the Opt=ModRedundant already appeared in the input line. Both methods gave almost identical results, with the same imaginary frequency and terminal carbon bond lengths.

The key difference between the two method is the second takes longer as is carried out in two steps as the part of the molecule is frozen then the other part optimised and then this done again to the other half. The first method does the optimisation all in one go and is good for small molecules, where the initial guess of the TS are good. Therefore the first method is adequate enough for this calculation. Below the data can be seen clearer in the table.

Chair TS optimisation methods

	TS(Berry)	TS ( Frozen coordinates)
Jmol
Terminal carbon bond length/Å	2.02	2.02
Imaginary frequency /cm-1	-818	-818
Imaginary frequency image	Vibration	Vibration
	Chair TS	DOI:10042/to-7178

Boat Transition Structure

The boat transition state will be optimised using the QST2 method, the reactants and products will be specified and the calculation will interpolate between them, both are 1,5-hexadiene. The chk file corresponding to the optimized Ci reactant molecule was used and then another window opened and the reactant molecule pasted a second time, which corresponded to the product molecule. Then the atoms numbered as shown by the image below.

Reactant (left) and Product(right)

The QST2 calculation was then ran with Opt+Freq, and optimised to a transition state. The TS (QST2) was used and the job was found to fail and the structure can be seen below. It looks similar to the chair transition structure but more dissociated. Therefore it can be assumed that the QST2 method is never going to locate the boat transition structure, if started from these reactant and product structures.

Failed QST2 boat TS

The molecule was adjusted by taking the original input file and the reactant and product geometries so that they are closer to the boat transition structure. This was done by changing the dihedral angle of C2-C3-C4-C5 to 0^o and C2-C3-C4 and C3-C4-C5 to 100^o to both product and reactant, so that they look like the structures shown below.

Reactant (left)and Product (right)

The jmol below shows the boat transition structure was computed and to check that is was a transition state the frequencies looked at. It was found that there was one imaginary frequency at -841 cm^-1 and its motion can be seen below, which corresponds to the bond formation.

Boat TS

	TS(Berry)
Jmol
Terminal carbon bond length/Å	2.14
Imaginary frequency /cm-1	-841
Imaginary frequency image	Vibration
	boat TS

Boat and Chair Transition Structure

Intrinsic Reaction Coordinate

The optimised chair and boat transition structures were looked at, the conformer of 1,5 hexadieiene they most resemble is hard to tell. If the bond which is forming is looked down then the chair resembles likeness to a gauche conformer. After the next step a more closer connection will be able to be made. It is therefore impossible to precisely predict which conformers of the reaction path that the transition state will lead to. The Intrinisic Reaction Coordinate (IRC) will allow the minimum energy path from a transition state to the local minimum on a potential energy surface to be followed by creating a series of geometries steps so that the gradient of the energy surface is steepest. This calculation was ran on both the optimised chair and boat structures, this will help to correlate the corresponding conformer.

In both cases the IRC was done by running the reaction coordinates in one direction due to the symmetric nature of the Cope rearrangement, the force constant was computed only once and the number of points along the IRC was set to 50. The results can be seen below. After this was done the file opened and the structures analysed. It was found that they had not reached their minimum yet, so there were three options to choose from to enable the minimum geometry to be reached. The first and second methods were run and the results can be seen below. The first method was used was to take the last point on the IRC and run a normal minimisation and the third was to compute all the force constants at each step. The second step was to restart the IRC and specify the number of points till the IRC reached a minimum, this was not used as the previously ran IRC for the chair can back after 24 steps even though 50 had been allowed so redoing this with more steps would still results in the same calculation. Below the conformation can be seen, the first approach was the fastest and the third is the most reliable but takes a longer time.

The chair TS took 24 steps when the IRC had the force constant once whereas it took the boat 29, so the full 50 points were not need. This showed that the restarting the IRC and specifying the number of points till the IRC reached a minimum would not be a good way to minimise the geometry. Also in both cases the gradient in very close to zero but, it could be closer. The energy has also nearly converged but this still has a bit to go, as it is not completely flat like when the force constant is always calculated. The geometries are nearing a conformer of the 1,5 hexadiene. The optimised file will be looked at below to compare them to the 1,5-hexadiene. If the energies are looked then it is closest to the gauche 6 in appendix 1 for the chair TS, it also resembles the gauche 2. For the boat the value is higher than the chair and it did not correlate to any of the conformers in appendix 1.

IRC calculation (force constant once)

	Chair	Boat
Structure at final IRC point	Pentahelicene	Pentahelicene
Number of steps	24	29
Energy/au	-231.688097	-231.679383
IRC pathway and gradient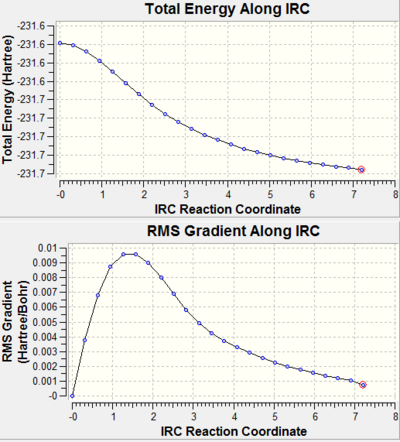

The energies were still not close enough to the conformer energies so then a normal minimisation HF/3-21G was run and this was compared to the conformer energies. In both cases the optimisation has caused the energy to become more negative so stabilised, they now have dihedral angles and energies closer to the ones in appendix 1. This method gives the closest energies to the conformers then the method above and below. The chair TS is exactly the same energy as the gauche 2 and has the same symmetry group C₂. The boat TS has exactly the same energy as the gauche 2 and the same symmetry group C₁. The exact energy was found and it can be seen that the boat TS is lower in energy then the chair by 0.62 kcal/mol and both TS connect to a gauche conformer.

Normal Optimisation calculation

	Chair	Boat
Otimised Structure	Pentahelicene	Pentahelicene
Energy/au	-231.691667	-231.692661
Dihedral angle (C(1)=C(2)-C(3)-C(4))/ 0	123.92	117.25, -121.34
Point group	C2	C1

The other steps suggested was to rerun the IRC but with all the force constants computed. This can be seen to be better then the first way as the energy converges for a larger number of reaction coordinates, and the gradient gets even close to zero and in the chair case is zero. Here again the boat required more steps to converge then the chair, the energies in both have decreased but the chair is lower is energy then the boat.

This method is suggested to have been the most reliable but it did take the longest time, to improve this the last point on the IRC could have been taken and a normal minimisation could have also be ran to see the connecting conformer more accurately. In the different calculation the chair TS does not have the bonds drawn in but the boat has had two bonds drawn in, this does not mean that the bond do not exist, just that the GaussView has not put it in. The greater number of points for convergence in energy and very close zero gradient suggest this method to be the most reliable. The chair TS has very similar energy as the gauche 2 so agrees with the above, but the boat TS does not have a match in this case.

IRC calculation (force constant always)

	Chair	Boat
Structure at final IRC point	Pentahelicene	Pentahelicene
Number of steps	47	51
Energy/au	-231.691664	-231.688064
IRC pathway and gradient

An analysis of the three methods was carried out for both the chair and boat TS and the data is tabulated above. The connecting conformer were found and using the data from the analysis in the first part of the report the bond lengths were compared to gauche 2 and 3. The two conformers have very similar bond lengths between the corresponding carbons. The only difference is in C (4)-C(3) which is larger in gauche 3 by 0.01 Å, but the error in bond distances ~ 0.01 Å, so this can be ignored. This is also how most of the methods vary to the comparison data by 0.01 Å. The only major difference is for the C(4)-C(3) boat when the force in measured once which is larger than then gauche 3 by 0.03 Å, this maybe due to computational errors.

Chair numbering

Boat numbering

Methods comparison (Chair)

	IRC (force Constant once)	Normal minimisation after IRC	IRC (force constant always)	Comparison data
	DOI:10042/to-7140	DOI:10042/to-7141	DOI:10042/to-7142	gauche 2
Energy/au	-231.68810	-231.69167	-231.69166	-231.69167
C(4)-C(3)/ Å	1.56	1.55	1.55	1.55
C(5)-C(4)/ Å	1.51	1.51	1.51	1.51
C(6)-C(5)/ Å	1.31	1.32	1.32	1.32

Methods comparison (Boat)

	IRC (force Constant once)	Normal minimisation after IRC	IRC (force constant always)	Comparison data
	DOI:10042/to-7143	DOI:10042/to-7144	DOI:10042/to-7145	gauche 3
Energy/au	-231.67938	-231.69266	-231.68806	-231.69266
C(4)-C(3)/ Å	1.59	1.55	1.56	1.56
C(5)-C(4)/ Å	1.51	1.51	1.51	1.51
C(6)-C(5)/ Å	1.31	1.32	1.32	1.32

Overall all three methods used product data very close to the conformers, which is assumed to be the connecting one. Also all the methods had data which is very similar and the difference is the same as the error in all but one value. The first method gave the most different bond lengths as both chair and boat had two distances which were not exactly the same. The second method for the chair is the same, but for the boat one value differes. The last method is the best as both the chair and boat have the same bond lengths to the corresponding conformers. This is also indicated by the greater convergence in the energy points and near zero gradient. The only difference was in the energy; here the second method gave the precise energies to the related conformers. The second method was ran very quickly as the first method was able to get close enough to the minimum point. All three methods are reasonable and have shown the balance of time and accuracy.

Activation energies

The activation energies were worked out by re-optimising the HF/3-21G chair and the boat using the higher basis set B3LYP/6-31G(d). It was optimised with the TS (Berny) and the frequency computed as well to ensure a TS had been made. A comparison of the data was carried out by looking at the geometries and energies of the reactants and TS and compared to literature data.

The energies could not be compared as two different methods had been used, but the energy gap between the transition state can be looked at. In both cases the chair is lower in energy so the more stable conformer, the chair is 0.016524 Hartrees (10.37 kcal/mol) in the HF/3-21G and is 0.01389 Hartrees ( 8.7161 kcal/mol) in the DFT B3LYP/6-31G(d) level of theory so the energy gap in DFT B3LYP/6-31G(d) is 1.65 kcal/mol less then HF/3-21G. So the DFT has the two transition states closer in energy.

The geometries were found to be similar as the angles and bond lengths were quite similar. The DFT method has shorter terminal C-C bond for the chair but longer in the boat. A shorter bond distance indicates a stronger attraction; this may be a possible reason for the higher stability for the chair. The angles are quite similar. There is a significant difference in the imaginary frequencies which is a difference of in 252(chair) and 311 (boat) cm-¹. The HF has more largely negative frequencies so smaller bond lengths as there is a reciprocal relationship, this agrees with the point above. As the geometries are fairly similar it is better to map the potential energies using the lower level theory and then re-optimise at higher levels, which was done in this case.

The DFT uses a higher level of theory so is more accurate, it cannot be compared to the conformer energies in the appendix as the minimum conformer has not been reached, so the log file was looked at to analyse the thermochemistry data and the activation energies calculated.

Chair TS

	HF/3-21G	DFT B3LYP/6-31G(d)
Structures
Energy/au	-231.619322	-234.556983
Terminal carbon bond length/Å	2.02	1.97
Adjacent carbon bond length/Å	1.39	1.41
Imaginary frequency/ cm-1	-818	-566
Angle C-C-C/ 0	120.50	119.95
	Chair TS	DOI:10042/to-7146

Boat TS

	HF/3-21G	DFT B3LYP/6-31G(d)
Structures
Energy/au	-231.602798	-234.543093
Terminal carbon bond length/Å	2.14	2.21
Adjacent carbon bond length/Å	1.38	1.39
Imaginary frequency/ cm-1	-841	-530
Angle C-C-C/ 0	121.65	122.27
	Boat TS	DOI:10042/to-7147

The table below was made by collecting the relevant data from previous calculations. The zero point energies were computed by running the FreqChk in Gaussian03W and the temperature altered to 0K (0.0001) and the results can be seen below. The zero point correction was computed and added to the electronic energy causing the energies to become more negative so more stabilised at lower temperatures. The relevant files for the boat and chair have been added above for anti Ci they are DFT anti C_i and HF anti C_i

Summary of energies (in hartree) for the C_i (anti 2) and chair and boat transition state

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466699	-231.461340	-234.556983	-234.414929	-234.409008
Boat TS	-231.602798	-231.450917	-231.445290	-234.543093	-234.402342	-234.396007
Reactant (anti2)	-231.692532	-231.539537	-231.532566	-234.611710	-234.49203	-234.461857

The activation energies were worked out by taking the difference between the reactant (anti 2) and the transition state (chair or boat) for the different temperatures respectively and converting the units with the conversion: 1 hartree = 627.509 kcal/mol.

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.69	34.06	33.16	33.5 ± 0.5
ΔE (Boat)	55.61	54.77	41.96	41.32	44.7 ± 2.0

It can be clearly seen for the experimental data at 0K that the DFT B3LYP/6-31G(d) is alot closer in the boat and chair TS then in HF/3-21G showing that the higher level theory is more accurate. This will therefore be the method used for the next part of the project rather then the HF. The table below shows that the DFT method is alot closer then the HF as the difference is smaller. The chair also has a smaller activation energy, so is lower in energy which can rationalised from less steric repulsion, so will be the TS for the kinetic pathway. The boat differs to experimental data more in the DFT model if the magnitude is looked at, this could be due to the computational calculation not accounting for all the steric effects.

Difference in Expt and Methods at 0K in ΔE/kcal/mol

	HF/3-21G	B3LYP/6-31G*
Chair	12.21	0.56
Boat	10.91	-2.74

The activation energies are similar to those provided in the appendix indicating the computations to have been successful, and any difference are to a few decimal places. The activation energies shows that the chair is lower in energy in both cases at both room temp and zero point energy. The chair is effect by the temperature change more then in the boat in both methods as the difference between temperatures in larger as shown by the table below. The chair has a larger ΔE between 298.15 and 0 K of 0.17 (HF) and 0.23 (DFT) kcal/mol, so the DFT changes the activation energy more.

Chair and boat ΔE/kcal/mol between 298.15 and 0 K

	HF/3-21G	B3LYP/6-31G*
Chair	1.01	0.89
Boat	0.84	0.63

The Diels Alder Cycloaddition

The Diels Alder is a cycloaddition reaction which is the concerted pericyclic reaction between the diene and dieneophile. The diene in this section is the cis butadiene and the dineohile the ethylene, which forms bonds by the π-orbitals overlapping. The transition state structure will be computed with the ideas learn from above and the shape of the molecular orbitals looked out. The MO concentrated on will be the HOMO and the LUMO and the symmetries looked at as the MO will the same symmetry will overlap. The secondary orbital interactions will be looked at which controls the regiochemistry of the reaction. This will be looked at in the second section between the maleic anhydride and cyclo-1,3-hexadiene.

Reactants

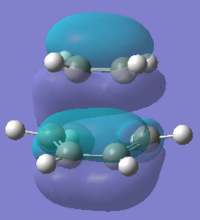
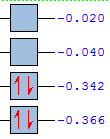
To compute the transition state, the reactants were optimised. Cis Butadiene was optimised using HF/3-21FG and can be seen below, it has a point group of C_2V. The ethene was also optimised separately. The optimised cis butediene was taken and the Diels Alder transition was tried to be made, the ethene was added with a bond distance of 2.2 Å between the terminal carbons. The MO can be seen below along with energies.

Diels Alder reagents

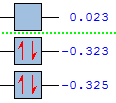
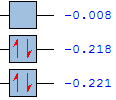
	Cis-Butadiene	Ethene
HOMO
Energy/au	-0.325	-0.387
Symmetry	antisymmetric(a)	symmetric (a)
LUMO
Energy/au	0.017	0.052
Symmetry	symmetric (a)	antisymmetric(a)

The orbitals are the π and π* made from p-orbitals of the reactants. The HOMO's are π and the LUMO's π*. It can be seen that the cis-butadiene HOMO and the ethene LUMO is anti-symmetric so the orbitals can overlap as they have the same symmetry and if the energy is close enough ( HOMO-LUMO gap = 0.377 au) then they will interact. The cis-butadiene LUMO and the ethene HOMO is symmetric and with a HOMO-LUMO gap = 0.404 au. Provided theses orbitals overlap the TS can be found as shown below sand its MO looked at.

Transition State

The transition state was looked at with both the semi-empirical and DFT-B3LYP/631G(d) (rather then HF as this was found to be more accurate). The method used was to optimise the TS by adding the two reactants into a file and running an Opt+Freq and optimising with TS(Berny) and calculating the force constant once with the additional words: Opt=NoEigen for both methods. The terminal bonds were also tried to be brought as close to 2.2 Å as possible. The transition state then guessed as it was know to be an envelope structure. The data collected can be seen below.

Optimised TS of the Diels Alder Reaction of butadiene and ethylene

Method	Semi-empricial/AM1	DFT-B3LYP/631G(d)
Optimised TS	dasad	dasad
Energy/ au	0.11162917	-234.54389655
Terminal carbon bond length/Å	2.12	2.27
Angle (C-C-C)/O	99.4	102.3
Imaginary frequency /cm-1	-956	-525
Imaginary frequency	Vibration	Vibration
log file	TS AM1	DOI:10042/to-7131

Both methods produced very similar TS, in the DFT the bond is slightly larger by 0.15Å, and the angle larger by 2.9 ⁰ . Both imaginary frequencies were found and they were showing the bond formation. The imaginary frequency shows the σ bonds being made, as they are moving at the same rate towards and away from the carbon.

The sp³-sp³ C-C bond is 1.54Å and a sp²-sp²C-C bond is 1.34Å. In the TS of both methods the C=C is 1.38 Å and the C-C is 1.40Å, this indicates that the C=C bond is breaking to form the C-C bond and π bond as the bond is getting closer to the C=C length. The van der Waals radius is 1.71 Å, and in the methods the bond length is AM1 (2.12 Å) and DFT (2.27 Å) this indicates that the bond formation has started as the length is less then the sum of the two van der Waals radii.

Optimised TS MO's of the Diels Alder Reaction of butadiene and ethylene

Method	Semi-empricial	DFT-B3LYP/631G(d)
HOMO
Symmetry	antisymmetric	symmetric
LUMO
Symmetry	symmetric	symmetric
HOMO-1
Symmetry	symmetric	antisymmetric
Energy/ au

Semiempirical/AM1 MO: The HOMO is anti-symmetric and has been made from anti symmetric HOMO butadiene and the ethene LUMO and the LUMO is symmetric and has been made from symmetric HOMO ethene and the butadiene LUMO, this illustrates the orbital symmetry rule. When the DFT higher level theory is ran the HOMO and HOMO-1 levels switch. This shows that the conservation of orbital symmetry has been preserved as the overlapped orbitals have the same symmetry as the reactant. Therefore the basis set can effect the energy level ordering. The HOMO-LUMO gap is AM1 (0.346 au) and DFT (0.226) so the orbitals are closer in the DFT and more accessible. The activation would have allowed for an energy comparison but it cannot be worked out as the DFT method was not used for the reactants, so the transition structures cannot be compared.

Cycloaddtion of Cyclohexa-1,3-diene and Maleic Anhydride

The Diels-Alder reaction of Cyclohexa-1,3-diene and Maleic Anhydride will be looked at. The reaction gives rise to two diasteroisomers: exo and endo. The endo adduct is the major product and the kinetic product and the calculation below will help to rationalise this.

Reactants

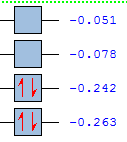
To compute the transition state, the reactant were optimised in this section as well. This time the Cyclohexa-1,3-diene and Maleic Anhydride were optimised and the semi-empirical/AM1 method was used to optimise them, the HOMO and LUMO molecular orbitals can be seen below.

Cycloaddition

	Cyclohexa-1,3-diene	Maleic Anhydride
HOMO
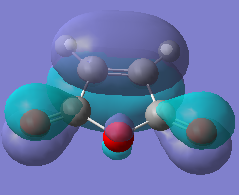Energy/au	-0.321	-0.441
Symmetry	antisymmetric(a)	symmetric (a)
LUMO
Energy/au	0.016	-0.059
Symmetry	symmetric (a)	antisymmetric(a)

The orbitals are π and π* from the p-orbitals of the reactants overlapping. The HOMO's are π and the LUMO's π*. It can be seen that the cyclohexadiene HOMO and the maleic anhydride LUMO is anti-symmetric, so the orbitals can overlappas they have the same symmetry and if the energy is close enough (HOMO-LUMO gap = 0.337 au) then they will interact. The cyclohexadiene LUMO and the maleic anhydride HOMO is symmetric and with a HOMO-LUMO gap = 0.338 au. Provided theses orbitals overlap the TS can be found as shown below and its MO looked at.

Transition States

The transition state was looked at with both the semi-empirical and DFT-B3LYP/631G(d). The method used was the same as for the reaction above to find both the exo and endo product to optimise the TS by adding the two reactants into a file and running an Opt+Freq and optimising with TS ( Berny) and calculating the force constant once with the additional words: Opt=NoEigen for both methods. The terminal bonds were also tried to be brought as close to 2.2 Å as possible.

The transition states were looked at in both methods used. The endo is lower in energy so the more stable conformer as suggest in literature . The difference in the semi-empirical is 0.001 au (0.63 kcal/mol)and the DFT is 0.004 au (2.56 kcal/mol). The differences are not large but the higher level of theory shows the energy gap to be larger so is more reliable to show that the endo is more stable, by 2.56 kcal/mol.

The table below also shows the imaginary frequency which indicates that the TS were made and the image shows the bond formation. The bonds distances were measures and the images can be seen with a colour code below. The underlined distances are the ones, which have change between the methods. In all four images the cyclohexadiene C=C and C-C bond length stayed the same. The most distinct difference was for the terminal C-C, the maleic anhydride C=C length stayed the same. The exo and endo terminal carbons stayed the same over the same method so for semi-empirical in exo was 2.17 and endo 2.16 then in DFT exo was 2.29 and endo 2.27 Å, in both cases the exo bond is longer. Therefore the bond is shorter for the endo product also explaining the relative stability as it has a more electron dense bond. The exo is actually the thermodynamic product as there is steric clash, as the endo product has 1,3 diaxial compressions between the cyclohexediene ring hydrogens and maleic anhydride. The stability of the endo can be seen for secondary orbital overlap which will be described below.

Looking at the frequencies it can be seen that the semi-empirical is more negative then the DFT in both the endo and exo, but they are in the same region respectively. The endo frequency is higher (less negative) then the exo is both methods this indicates that the bonds are shorter and it is a reciprocal relationship and the potential energy maximum is lower hence the more favourable product. The angles are all very similar, there is however some strain in the exo product as the angle is slightly less.

Optimised TS of the Cycloaddition- EXO and ENDO

Method	Semi-empricial/AM1	DFT-B3LYP/631G(d)	Semi-empricial/AM1	DFT-B3LYP/631G(d)
	Exo	Exo	Endo	Endo
Optimised TS	dasad	dasad	dasad	dasad
Energy/ au	-0.05050250	-612.67931095	-0.05150479	-612.68339679
Terminal carbon bond length/Å	2.17	2.29	2.16	2.27
Bond length/Å
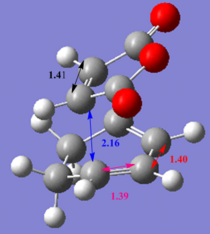Angle (C-C-C)/O	107.5	107.0	107.6	107.1
Imaginary frequency /cm-1	-812	-448	-806	-447
Imaginary frequency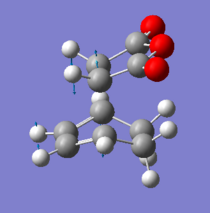
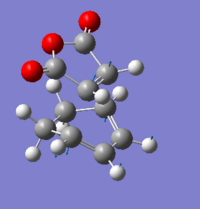log file	TS AM1 (file too large to upload)	DOI:10042/to-7156	DOI:10042/to-7155	DOI:10042/to-7157

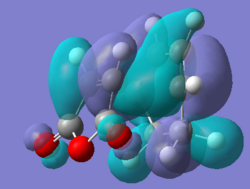
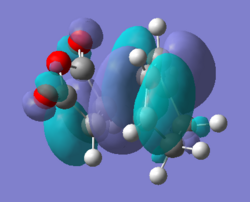
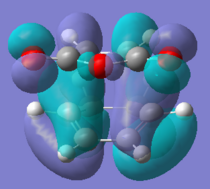
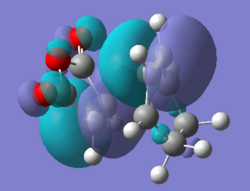
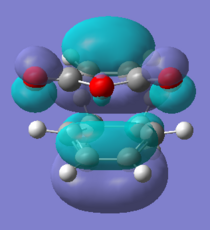
All the orbitals shown below are anti-symmetric, the HOMO-1 and LUMO+1 were looked at to see the secondary orbital overlap more evidently. The HOMO orbitals shows the σ bonding interaction between the reactants. The HOMO orbitals are made from the HOMO of cyclohexadiene and LUMO for maleic anhydride, the LUMO cannot be rationalised as in the other Diels Alder so it can be assumed that there other interactions are going on.

Optimised TS MO's of cycloadditon- EXO and endo

Method	Semi-empricial	DFT-B3LYP/631G(d)	Semi-empricial	DFT-B3LYP/631G(d)
	Exo	Exo	Endo	Endo
HOMO
Symmetry	antisymmetric	antisymmetric	antisymmetric	antisymmetric
LUMO
Symmetry	antisymmetric	antisymmetric	antisymmetric	antisymmetric
HOMO-1
LUMO+1
Energy/ au

Secondary Orbital Overlap

The -(C=O)-O-(C=O)- was found to be 2.99 Å in the endo and 3.02 Å for exo, the shorter endo distance could be related to the secondary orbital overlap. The secondary orbital overlap can be seen in the image below and it the interaction of the π- bonds of the cyclohexadiene and π* of C=O, this gives the kinetic product. The secondary orbital overlap stabilises the endo TS and the correct orientation of the orbitals is seen, as shown by the image below. The overlap are not bond formations but rather stabilisation interactions. This is more evident if the MO are analysed further. The endo product is lower in energy due to the lower energy, this was said in the endo rule which says the more stable transition state is the one which has the maximum overlap of it molecular orbitals, so its secondary orbital overlap is greater.

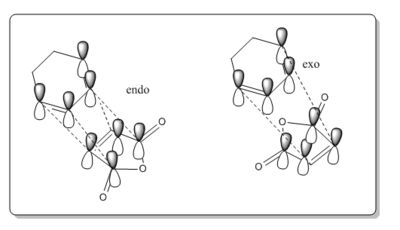
The HOMO of the exo and endo both have nodal planes, but the HOMO does not contain the overlap above, and are lower in energy for both methods. Therefore the HOMO-1 and LUMO+1 orbitals were looked at. They may show more clearly why the endo is more stable as the π interactions may be seen more clearly from the HOMO-1 and LUMO +1 orbitals. It is not as clear as expected to see the secondary orbital over form the MO, as it was when looking at the frontier orbitals above. This may mean that in the case the endo is not being stabilised by this but rather the exo steric effects of the bridging head and hydrogens close by. This cases the energy to be greater. Therefore for the computational analysis suggest a compromise between the steric and secondary orbital overlap.

In literatures above the secondary orbtial overlape exists but it is not as clearly visible. The idea of steric could be further investigated to see if this is greater effect by adding different R groupd to the reactants and looking the effect. The other consideration is that the different methods used gave different orbitals as seen in the previous examples, therefore another basis could be investigated to see if the secondary orbital could be seen. In a previous computation lab my project looked at benzocantharidin as the exo stereosiomer and isobenzocantharidin as the endo one , the Diel-Alder reaction was shown to be reversible, which accounts for the high stereoselectivity in favour the exo isomer. It gave benzocantharidin in a 95 % yield and 5% isobenzocantharidin. This shows that sterics does play an important part but now the exo product dominat. This shows that the method used in looking at the HOMO-LUMO could be reconsidered and there is a compromise between secondary orbital overlap and sterics which is interesting to see from the quantum mechanical analysis of the transition states.

Activation energy

The reactants were optimised using the semi-empirical method and the TS structure was also found using this method so the activation energy can be calculated as follows. The endo product has a smaller activation energy so is the kinetic product, there is only a difference of 0.63 kcal/mol, if a higher level basis set was used the energy difference would have been larger and more accurate and closer to experimental data. The 0K energy could have also been looked at by doing to Opt+Freq of the reactants and then doing a FreqChK calculation, this would have enabled the effect of 0K on the transition states in comparison to 298.15 K, to be made.

The data below suggests that the exo is higher in energy and has a greater activation energy so will be the thermodynamic product, whereas the endo is lower in energy and has a smaller activation energy so is the kinetic product. The reason behind this have been looked at before. Another point to consider is the Boltzmann distribution of the TS, as see the ratio of the exo and endo products. This was done by converting hartrees to kJ/mol with the conversion of 1 Hartree= 2625.5 kJ/mol, then knowing that ΔG^o=-RTlnK. Therefore K can be worked out so the ratio of exo and endo be seen where the exo is slight less then the endo, indicating the that the endo is the dominant product from this analysis too.

Activation energy using semi-emprical at 298.15K

	Exo	Endo
Sum of reactant energy/ au	-0.09414155	-
TS energy/ au	-0.05050250	-0.05150479
Activation energy/ au	0.04363905	0.04263676
Activation energy/ kJ/mol	114.57	111.94
K (equi constant)	0.9548	0.9558
Ratio	0.9989	1.0000

From the energies it can be predicted which may be the kinetic and which the thermodynamic product, but the computation analysis does not tell us this nor does it give any reasoning for it. This can only be worked out experimentally. It also does not account for example solvent effects, which may affect the dominant product.

Conclusion

Overall some interesting computational analysis was done and some conclusions gathered from the comparison of the compounds. The computational analysis at times could be quite length, but is a very useful technique which is reliable as the agreement to literature is good. The transition state is a very useful techniques for analysis of the reactions, however the computational method required initial guesses of the transition states to be made which were close to the real transition state. This would therefore not be useful to analyse reactions where the TS were not known.

The Cope rearrangement and the Diels Alder reaction show how the transition state analysis was important. The use of molecular orbitals and activation energies helped to analyse them further.The different methods used also showed the how analysis could be different. In the Cope rearrangement the "boat" transition structure was seen to be higher in energy and through different methods the optimised structures seen. The Diels-Alder reaction of Cyclohexa-1,3-diene and Maleic Anhydride showed that the endo was the major and kinetic product due to a sterics and the endo rule. The stability of the product was seen from the activation energies and the molecular orbitals gave information on the stereoselectivity. The computations also allowed the prediction for allowed or disallowed reactions by looking at the molecular orbital symmetry.

The investigation could have been developed by looked at other reactions with bulkier groups and other basis sets. However the would have taken more time and the DFT B3LYP/6-31G(d) gave a compromise between accuracy and time.The boltzmann distribution could also have been consider when looking at the 1,5-dihexadiene conformers and seeing how the activation energy related to the ratio of the products and then seen if energy correlated to the ratios.