Rep:Mod:s j hines phys
Introduction
The main aim for this computational laboratory was to examine transition structures for potential energy surfaces for two reactions:
In previous modules of the course, the 'Molecular Mechanics' method has been used for optimisation and other calculations. Whilst this is an effective method for determining the various possible geometries of the molecules in quetion, it cannot be used to study reactions, e.g. the breaking or forming of bonds, change in the type of bonding or changes in electron distribution cannot be calculated through this method.
In order to study the desired factors stated above, there is a need to numerically solve the Schrodinger Equation. In order to do this, molecular orbital methods are used in the calculations. The local shape of the potential energy surface can be used to determine:
- Geometry of trasition structures
- Reactions Paths
- Energy Barrier Heights
Three methods will be studies for transition structure optimisation. Calculating the force constants at the start of the calculation, using the 'redundant coordinate editor', and using the QST2 method.
Cope Rearrangement
The first part of the laboratory involved the study of the Cope Rearrangement of 1,5-Hexadiene according to the scheme below:
The 'low-energy minima' will be found, along with the transition structures on the C6H10 potential energy surface. This information will be analysed, thus allowing a conclusion to be reached as regards to the mechanism of the reaction. Previous studies have been carried out on this reaction, with the 'concerted' mechanism widely accepted as correct. This laboratory will determine whether the reaction occurs via a 'chair' or 'boat' transition state. For accurate measurements of energies/enthalpies, using the 'Gaussian' program, the B3LYP/6-31G* level of theory is used here.

Optimising Products and Reactants
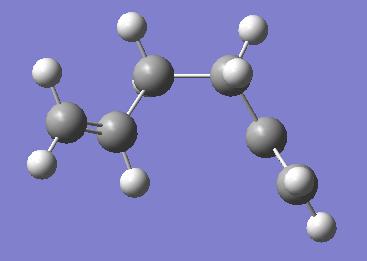
Firstly, a molecule of 1,5-hexadiene was constructed in 'GaussView' with the four central carbon atoms having anti linkage. This molecule was then optimised, using the Hartree-Fock method with the 3/21G basis set. A snapshot was taken of the resultant molecules is shown below. The 'symmetrize' option was used in order to find a point group for the molecule. This was found to be C2.

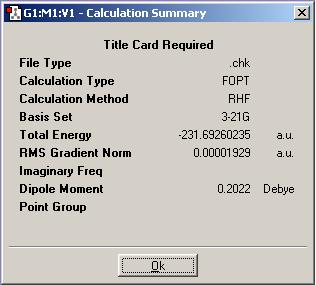
The 'summary' of the calculation (shown below) gives the energy value of the structure - in Hartrees.
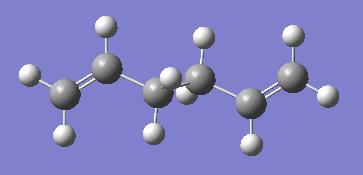
Exactly the same procedure was carried out for the molecule with the central four carbon atoms having gauche linkage. The molecule is shown below. It's point group is C1
The 'summary' of the calculation (shown below) gives the energy value of the structure - in Hartrees.

The two structures here are very similar in energy: the gauche conformer at -231.69266 Hartrees, the anti conformer at -231.69260 Hartrees. The relative energy in kcal/mol for the anti is 0.04. Maybe it would be expected that the gauche conformation might have a higher energy than the anti, the terminal carbons being bent towards each other, but this is not the case. A table of the different structures for both anti- and gauche- linkages is shown in appendix 1 of the course notes. The structures obtained here correspond to the 'anti1' and 'gauche 3' in the table. The energies found correspond exactly to those shown, and the lowest energy conformations have been successfully found, 'gauche3' being the lowest and 'anti1' the second lowest.
Finally, the same procedure was carried out for an alternative conformation of the molecule with the central four carbon atoms having anti linkage. The molecule is shown below. It's point group is Ci
The 'summary' of the calculation (shown below) gives the energy value of the structure - in Hartrees.
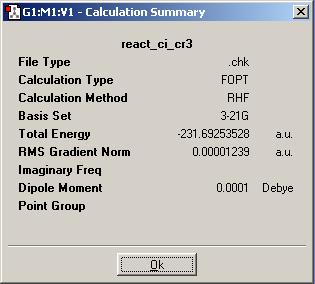
Appendix 1 contains the molecule above as 'anti2'. The energy found in the calculation again exactly matches the one in this table.
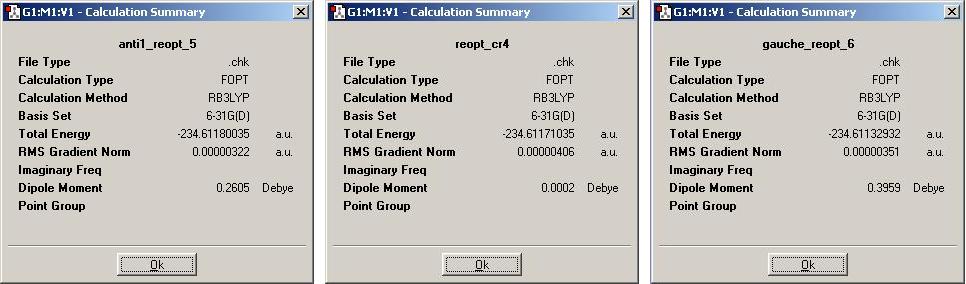
The three structures here were then reoptimised using the more accurate 'density functional B3LYP method' with the 6/31G* basis set. The new geometries of the molecules, anti1, anti2 and gauche3 (respectively) are shown below. As it is possible to see, the change in overall geometry has hardly altered at all.

It is a different story for the energies that the calculation has evolved. These, shown below, are very different from the previous values from the less accurate method (anti, anti2, gauche3 respectively).
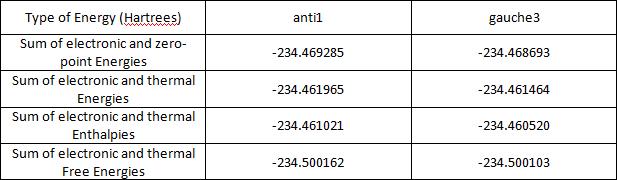
The energies shown so far are for the molecule on the 'bare potential energy surface.' At this point they are not sufficient to be compared to experimentally determined values. Other terms need to be included, thus a frequency calculation is needed. This calculation can be used to confirm whether the critical point is a minimum. If this is true, all the frequencies that are calculated are real and positive. This calculation was performed on the 'anti' and 'gauche3' molecules, all the frequencies were real and positive. Energy terms needed can be extracted from the results file. An explanation of these is given here. The values are tabulate below for the anti1 and gauche3 conformations.
Optimising the 'Chair' Transition State
An allyl fragment was optimised using the HF/3-21G method. This result was then used to construct the chair transition state shown above. The allyl fragments were placed at 2.2 angstroms apart at the start of this calculation. Optimised allyl fragment:
The transition state was then optimised using the HF/3-21G method, by calculating the force constants once at the start of the calculation. The structure evolved from this calculation did indeed correspond to appendix 2 of the course notes. Also the expected imaginary frequency of -818 cm-1 was found:
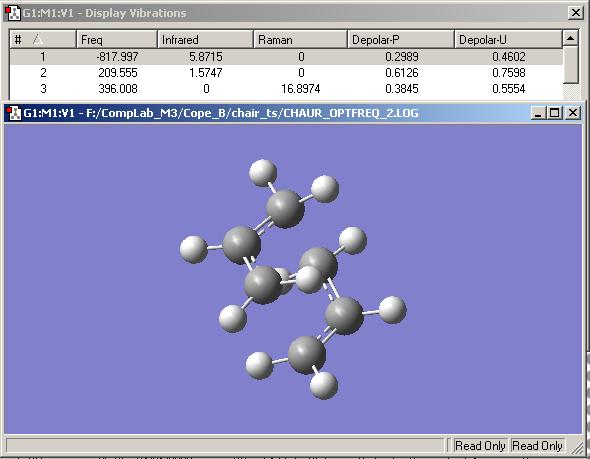
An alternative method was then used to optimise the transition state; use of the redundant coordinate editor, as described in the course notes. Bond lengths between the pairs of carbons forming/breaking bonds were taken for comparison to the previous transition state optimisation's values. The structure found from the second optimisation is not shown here because there appears to be no noticeable visible difference whatsoever between the structures. This is reflected in the bond lengths mentioned. For the first method, these are 2.02051 angstroms, whereas for the second they are 2.02043 angstroms for one and 2.02030 ansgtroms for the other; a tiny difference.
In order to calculate the activation energy of the reaction, the optimised transition structure here needs to be optimised with frequency calculations using the density-functional B3LYP method with the 6-31G* basis set. The geometry of the optimised structures for each level of theory are very similar, however there is a relatively large energy difference between them.
A question stated was 'Which conformers of 1,5-hexadiene do you think they connect?'. Looking at the possible conformers, it is not possible to make any sort of prediction on this. The 'Intrinsic Reaction Coordinate' (IRC) method follows the 'minimum energy path from a transition structure down to its local minimum on a potential energy surface. It creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest.' (notes) This calculation was carried out using HF/3-21G. It was possible to see how the calculation had progressed so far, as there were structures shown for different stages of the calculation - firstly the calculation was run to 50 points along the 'IRC'. The calculation was then performed using 250 points to yield this structure (more thoroughly/accurately optimised):
Other methods that were carried out to yield a similar transition structure were to take the last point on the IRC and run a minimisation or to make sure the force constants are computed at every stage, rather than just the start.
Optimising the 'Boat' Transition State
The 'boat' transition state was optimised using the 'QST2' method. This method performs a calculation such that one can provide the reactant molecule and product molecule, and a transition structure is found for the reaction. For the reaction in question, it was important to specify explicitly which atoms were which when moving from the reactant molecule to the product molecule. An example of this is shown in the notes. This involved modification of the anti2 structure previous calculated - arranging the molcule to look like the boat transition state and numbering the reactants and products as discussed. Without this pre-rearrangement to orientate the molecule to look like the boat transition state, the calculation does not complete properly:
The calculation was performed with the two preparatory factors considered. A good indication that the optimisation was successful was the fact that there was an imaginary frequency that corresponds to the bonds breaking/forming between the pairs of carbon atoms, at -840 cm -1:
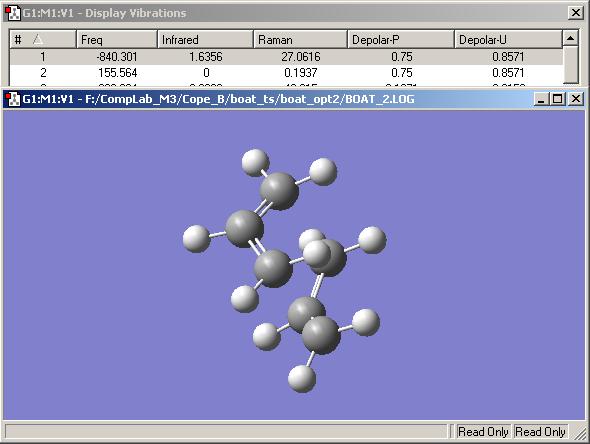
In order to calculate the activation energy of the reaction, the optimised transition structure here needs to be optimised with frequency calculations using the density-functional B3LYP method with the 6-31G* basis set. The geometry of the optimised structures for each level of theory are very similar, however there is a relatively large energy difference between them.
Diels-Alder Cycloaddition
Cis-Butadiene Reaction with Ethylene
The second reaction investigated was that between cis-butadiene and ethylene, as in the scheme below.
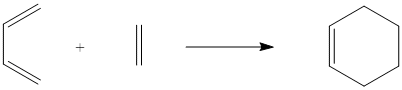
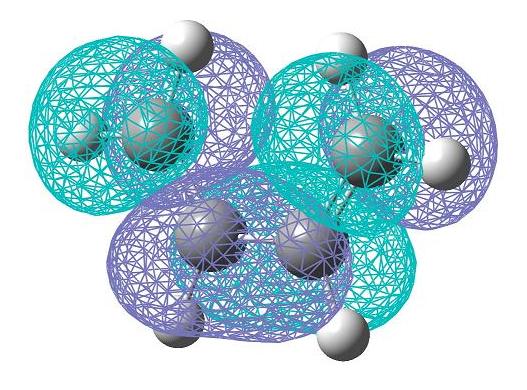
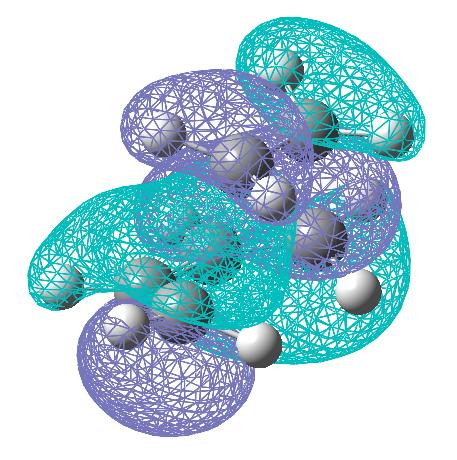
Cis-butadiene was constructed using GaussView. This molecule was then optimised using the density functional B3LYP method with the 6-31G* basis set. This allowed the HOMO (bottom) and LUMO (top) to be computed. A representation of these on the optimised structure are pictured here. It is possible to see that these molecular orbitals are anti-symmetric with respect to the plane.
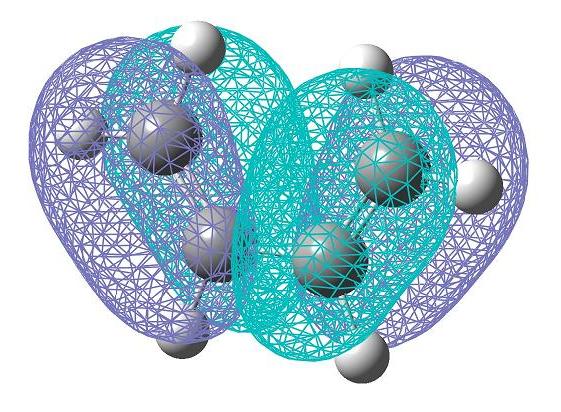
The trasition state structure here can be thought of that in the diagram below. This allows the π orbitals of the ethylene to react with the π orbitals of the cis-butadiene. In the previous exercise, the guess distance between the fragments was 2.2 angstroms. This was the same as here.

The transition state was optimised with frequency calculation using the AM1 semi-empirical molecular orbital method. This calculation confirmed that the transition state structure here is the true one for the Diels Alder reaction being studied, due to the fact that the imaginary frequency here at -956 cm-1 corresponds to the forming of the desired bonds.
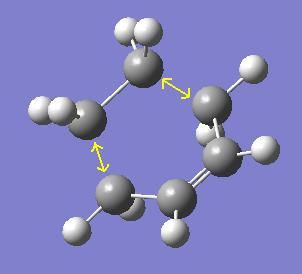
This frequency is illustrated below. It shows the bonds being formed in a synchronous fashion. This is different to the lowest possible real frequency 147 cm-1, which is asynchronous.
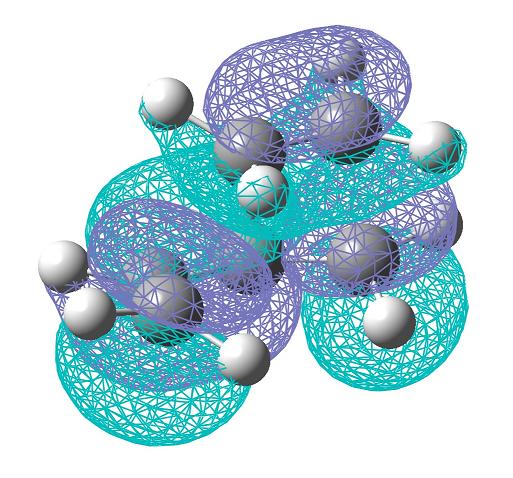
The HOMO (bottom) and LUMO (top) were then plotted. The HOMO here is antisymmetric, but the LUMO is symmetric.
The optimisation of the transition state above was carried out via calculating the force constants at the start of the calculation. It was also carried out using the redundant coordinate editor to allow comparison. A similar geometry, as expected, was formed:
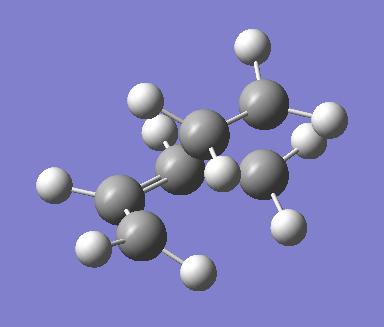
The partially formed C-C bond lengths for the first optimisation were 2.11920 angstroms and 2.11932 angstroms. These are very similar to those found in the second optimisation, at 2.11889 angstroms each. These compared to typical a C-C bond length of around 1.50 angstroms and a C=C bond length of around 1.32 angstroms. The van der Waal radius of a carbon atom is 1.70 angstroms. The partially formed bonds in the transition state are therefore much longer and weaker than a full C-C or C=C is.
