Jump to content

Rep:Mod:s j hines org

From ChemWiki

Molecular Mechanics

Introduction

The aim of the first part of this experiment was use molecular mechanics to investigate the geometry and regioselectivity in the following four instances:

• Hydrogenation of a cyclopentadiene dimer

• Stereochemistry of nucleophilic addition to two different NAD+ analogues

• Conformation/atropisomerism of a large ring ketone intermediate in one method of synthesis of 'Taxol'

• How conformation effects the rate of peptide synthesis


Molecular mechanics is a very useful tool when attempting to solve problems such as the ones addressed in this report. Physical models which can be easily made are very limited in the information they provide about the molecule - they can only provide a qualititive review of the properties sought. This method allows more complex and quantitative information to be calculated in a relatively quick time, for example if one wanted to know which conformation of a molecule is the one that will take part in a particular reaction. There are five factors that the method takes into consideration:

  1. All diatomic bond stretches
  2. All triatomic bond angle deformations
  3. All tetraatomic bond torsions
  4. All van der Waal interactions
  5. All electrostatic attractions of individual bond dipoles


Consideration of these above factors allow the model to produce a total energy, and the most stable geometry of a particular molecule. Due to the simplicity of the model, it is not able to analyse chemical reactions or molecules with unusual bonding e.g. not two-centre-two-electron bonds, accurately.


Hydrogenation of a Cyclopentadiene Dimer

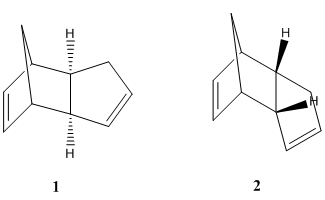
When cyclopentadiene dimerises, there are two possible stereoisomers that could be made, either the exo product (1) or the endo product (2). The preference as to which of the dimers is formed is controlled by one of two factors, thermodynamics or kinetics. The thermodynamically favoured product would be taking into account the stability of each of the product molecules. The kinetically favoured product takes into account the stability of the transition state. Molecular mechanics, in this case, was employed to minimise the energy and geometry of each of the molecules (left). The dimer molecule with the lowest energy is the most stable, thus is the thermodynamically favoured product. Out of the two dimers pictured here, the one that is formed is the endo product, (2). We would expect that if the dimerisation of cyclopentadiene is thermodynamically controlled, then this would be the molecule with the lowest overall evergy. However this was NOT the case. The total energy for 1 was 31.8824 kcal/mol, whereas for 2 it was 34.0131 kcal/mol, meaning it is actually higher in energy (found to be mainly due to the extra torsional strain of the molecule). Therefore it is possible to draw the conclusion that the dimeristation of cyclopentadiene is kinetically controlled.


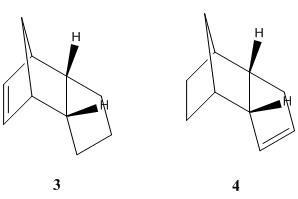
The endo dimer (2) contains two carbon-carbon double bonds, thus when hydrogenation takes place, there is a choice of which double bond takes part in the reaction. This gives rise to two possible products (3) and (4) - shown right. Molecular mechanics was again used to minimise energy and geometry of the two possible products. The relative overall energies of the two possible molecules can be compared in order to determine which of the two double bonds in (2) is more favourable to take part in hydrogenation. The overall energy of (4), 31.1530 kcal/mol, was found to be less than the energy of (3), at 35.9309 kcal/mol. Further analysis showed that the origin of the extra strain of product (4) came from bending, 4.3470 kcal/mol higher than in (3), and 1,4 van der Waal's interactions, 1.2400 kcal/mol higher than in (3). There were also minor difference in stretching, torsion and hydrogen bond energies, however these did not make a telling contribution to the difference in stabilities between the two molecules. These overall energy values for (3) and (4) give an indication of which double bond of the endo dimer (2) is more available for hydrogenation, in a thermodynamic sense. The hydrogenation product with the lowest energy is (4), therefore the double bond that is more thermodynamically favourable must be the double bond on the left in molecule (3).

Stereochemistry of Nucleophilic Addition to Two Different NAD+ Analogues

Pentahelicene


The molecule on the left is an optically active derivative of the chiral amino-alcohol, prolinol. Molecular mechanics has been used to minimise the energy and geometry. Whilst the limitations of this model do not allow it to be used for analysis of reactions (the molecule has to be considered by itself - an error message appears if the reactants are included), this technique still can be effective in predicting stereochemical consequences, as shown here. The total energy of the molecule, as calculated by this method, varied depending on the starting point of the construction. However, the geometry of the carbonyl with respect to the aromatic ring did not alter in a way significant enough to affect the mechanism of the following studied reaction. This molecule will react with the Grignard reagent, methyl magnesium iodide, causing a methyl group to be attached to the pyridinium ring in the 4-position.
The orientation of the carbonyl is very important in determining which face of the pyridinium ring the methyl is attached to. This is due to the transition state of the reaction. The reference[1] shows that the reaction proceeds through coordination of the magnesium to the oxygen. This causes the delivery of the methyl group to be from a specific face. If one rotates the molecule on the left in order to check the carbonyl group orientation, it is found that it is not planar with respect to the pyridinium ring. Once rotated appropriately, if the methyl group of this ring is pointing directly into the plane of the screen, it is seen that the carbonyl group is pointing slightly below the plane of the ring. Coordination of the magnesium metal to this oxygen atom fixes the incoming methyl group, causing it to be attached to the same face as the direction in which the carbonyl was pointing. This rationalises the stereochemistry present of the alkylation product (right).


Pentahelicene


The second reaction that was studied was the reaction of the molecule shown left with aniline to form a derivative in which an NHR group has been added 1,4 to the pyridinium ring (where R = phenyl). The energy and geometry was once again calculated using the molecular mechanics method. The resulting molecule is showen left. The orientation of carbonyl group in the starting molecule is essential in determining the stereochemical consequences of the reaction. The incoming NHR group has the possibility of attaching to the pyridinium ring at either face. It is the position of the carbonyl group that determines exactly which face this is[2]. If the starting molecule is rotated such that the pyridinium ring, and the adjacent ring are flat in the plane of the screen, then it is clear that the carbonyl is pointing almost straight into the plane of the screen. This orientation prevents the NHR group approaching from the back face to the carbon in question to react with it. Again, molecular mechanics has provided a simple explanation as to how the reaction proceeds with the observed stereochemistry to produce the product shown right, with the NHR having attached to the front face, with the more bulky R group pointing forwards. A very obvious difference to the previous reaction in this section is that the carbonyl did NOT take part in the reaction, nor was it used for any coordination purposes.

Pentahelicene

Conformation/Atropisomerism of a Large Ring Ketone Intermediate in One Method of Synthesis of 'Taxol'

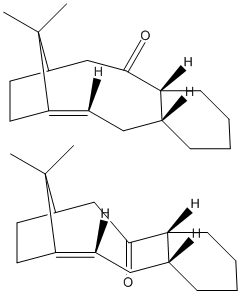
The two 2D representations below show two atropisomers of an important intermediate within the synthesis of the drug, 'Taxol'. Molecular mechanics was used to analyse the two isomers in order to calculate their comparative energies, thus give an idea as to which of the two is most stable. The optimised geometries produced using this model are shown to the right in the two 3D representations. The isomer of the lowest energy (48.1469 kcal/mol), thus the most stable, was found to be the isomer that contains the carbonyl group pointing down (bottom 2D picture, right hand 3D). This is when this part of the molecule is effectively in a 'chair' conformation, as in the reference[3]. The isomer that contains the carbonyl group pointing up (top 2D picture, left hand 3D) has an energy of 48.8906 kcal/mol. This is when this part of the molecule is effectively in a 'twist-boat' conformation, as in the reference[3].

Pentahelicene
Pentahelicene

The C=C double bond in the bridge-head bicyclic alkene reacts much more slowly than is expected. This is due to a concept known as ‘hyperstability’[4][5][6]. This molecule is classed as a 'hyperstable' alkene because, as Schleyer et al. say[4] [5] [6], of the bridghead position of the C=C double bond. The 'parent hydrocarbon' is more strained than the bridgehead system shown in each of the isomers of the above molecule. A second work by Schleyer et al. mentions that mostly it is unusual to see C=C double bonds in such a bridgehead position to be this stable, however the increased stability is explained by the large size of the molecule and the fact that there is more than one ring in the system. Molecular mechanics, using the MM2 method, as was used here in this secton, was the model used by Schleyer et al. to explain this concept[4] [5] [6]. Just by qualitative analysis of the position of each of the C=C double bonds in the geometrry optimised 3D representations above, it can be seen that they are not being exhibited to as much strain as they would be if they were not in their particular bridgehead position.

How Conformation Affects the Rate of Peptide Synthesis

Pentahelicene
Pentahelicene

The two isomers of a molecule left (top), both cisdecalin derivatives with its N subsituent in the axial position, then equatorial position respectively, show different kinetic behaviour than the two pictured left (bottom), both transdecalin derivatives with its N subsituent in the axial position, then equatorial position respectively, with respect to hydrolysis of the peptide contained within the molecule. The first set have a half life of 21 minutes, whereas the second set have a half life of 840 minutes. The MM2 method of molecular mechanics was used in an attempt to explain this difference in reactivity. The energy and geometry of all four were minimised with the results shown left. The cisdecalin derivative with the equatorial N substituent was the isomer with the lowest comparative energy at 13.3756 kcal/mol. This compared to the equivalent transdecalin derivative which had a higher energy of 18.3285 kcal/mol. There is a similar trend when comparing the isomers with the N substituent in an axial positon, with the cisdecalin derivative at 19.6636 kcal/mol and the transdecalin derivative at 23.3418 kcal/mol. This evidence indicates an increased stability of the cisdecalin derivative.

Pentahelicene
Pentahelicene

If you rotate each of the 3D representations appropriately, as to view the carbonyl oxygen with respect to the hydrogen atom attached oxygen of the alcohol, it is seen that hydrogen bonding is occurring here in the cisdecalin derivative (both when N substituent is axial and equatorial). This is not the case for either of the transdecalin derivative isomers. This is a major factor which defines the extra stability with respect to the non-hydrogen bonding alternative. The greater stability of the cisdecalin derivative is not the only evidence as to a reason why it has a shorter half life with respect to peptide hydrolysis. The ability to hydrolyse the peptide bond depends a lot on the orietation of the carbonyl group compared to that of the OH group. The distance and angle between these two groups is not favourable for hydrolysis in the transdecalin derivative (both types) as can be visualised by rotation of the 3D representations (left). The carbonyl group is far from the OH group and is pointing away from it. However, in both the cisdecalin derivatives, it can be seen that the carbonyl group is much closer and at a much more favourable angle for approach of the OH.

All of the evidence here, collected through analysis of the molecules using molecular mechanics, rationalises why there is a far shorter half life for the reaction in question (below) - the fact that the most stable conformation is also the conformation which allows favourable approach of the OH group to the CO.

The half life of a peptide bond at 298K and pH neutral is 500 years. The fact that the half life here is far less than that value can be attributed to two factors. Due to fact that this is an intramolecular reaction; the two groups participating in it are maintained in a position favourable to react next to each other or 'sustained proximity'[7]. The reaction is allowed to proceed with relief of steric strain[7].

Semi-empirical Molecular Orbital Theory

Introduction

The model used in part one has been shown as a very useful method in rationalising and predicting certain properties of molecules and stereochemical consequences of some reactions. However, molecular mechanics cannot be used to analyse stereoselectivity of reaactions where it is determined by electronic properties, because this method does not take into account how electrons affect the product molecule. Therefore in part 2, a more sophisticated model has been used, the so called 'HF/STO-3G self-consistent-field molecular orbital method' and then the further accurate 'density-functional B3LYP/6-31G(d) approach'.


Regioselective Addition of Dichlorocarbene

[8]
Pentahelicene

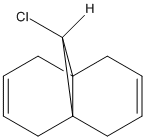This section involved calculation of the geometry of the molecule pictured on the far left. It was calculated using the same method as in the previous sections, molecular mechanics (MM2), then also the two new methods mentioned in the introduction above, HF/STO-3G self-consistent-field molecular orbital method and then the density-functional B3LYP/6-31G(d) method. The 3-D representation of the molecule (left) shows the optimised geometry using the HF/STO-3G method. The difference in appearance of this compared to the ones obtained for the other two method is very small and hardly noticeable, and as a consequence, there is not a need to show all three of them here. The extremely slight difference in the predicted structures between each of the methods is the position of the C-Cl group in the compound with respect to the bicyclic system. The more accurate the method used to optimise the geometry, the further the Cl atom moves away from the ring containing the double bond endo to the C-Cl group. The reaction to be studied here; the reaction of this compound with the electrophilic reagent, dichlorocarbene. As stated in the introduction to this section, a method is needed that takes into account orbital interactions because this reaction is dependant upon these factors. Here, the HF/STO-3G method is important in allowing an approximate representation of the valence-electron molecular wavefunction to be estimated, rather than to calculate the overall geometry of the starting compound (left). Through this method, the molecular orbitals of the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 levels have been calculated and pictured below.































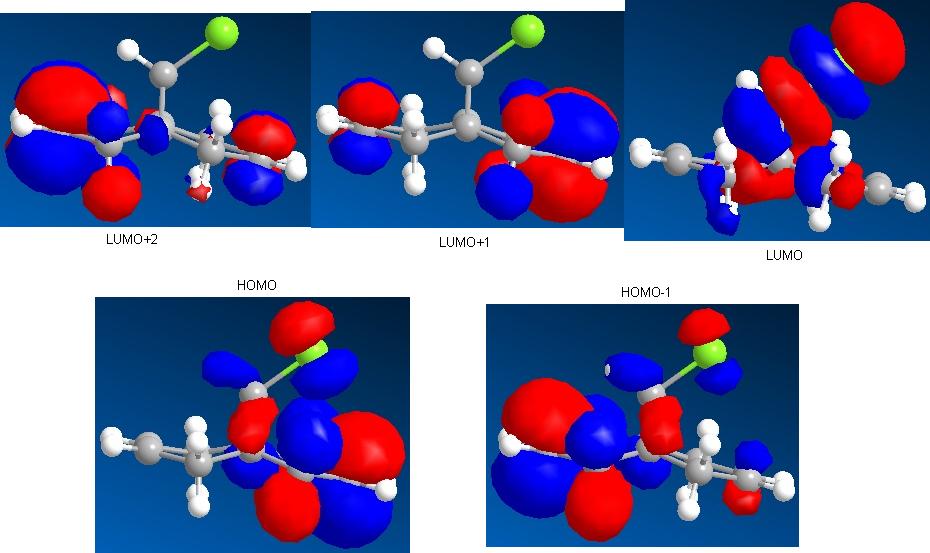
Once again, the main difference between molecular mechanics and molecular orbital methods is the consideration of the electronic effects within the molecule. For this to be carried out, a quantum mechanical approach is needed. Obviously the simple molecular mechanics method completely disregards this.

HF/STO-3G:-

The Hamiltionian used is the 'Hartree-Fock' Hamiltonian. In this exercise, it takes into account paired electrons only (singlet states). The minimal basis set is used here. It is the simplest molecular orbital method calculation that can be made, thus it only takes a few minutes to complete, compared to the following method that can take 1-2 hours

B3LYP/6-31G(d):-

An alternative Hamiltonian is used here than above for this density functional method. It is more accurate than the first molecular orbital method above because it takes into account 'electron correlation', and also a 'double basis set'. The '(d)' represents the 'polarisation function' of the d orbital for carbon.[9]

The molecule in 2D and 3D representations at the start of this section contains two double bonds, one in each of the six-membered rings. The next calculations involved the comparison of this molecule (has Cs symmetry) and the monohydrogenated derivative of it (hydrogenated at the double bond anti to the C-Cl group, (found not to have Cs symmetry). The molecules were constructed, then their geometry minimised using the density functional molecular orbital method. This calculation also allowed analysis of stretching vibrations within each molecule, in particular the C=C and C-Cl frequencies. In the starting molecule, it was expected that there will be two stretching frequencies for C=C as it contains two double bonds. This was found to be true, these were at 1740.69 cm-1 (double bond anti to C-Cl) and 1760.91 cm-1 (double bond syn to C-Cl). In the monohydrogenated form, obviously there is only one C=C stretching frequency left, for the remaining double bond, this was found to be at 1761 cm-1. Along with the stretches outlined here, there were also three C-Cl stretching frequencies for each molecule. For the diene, the three frequencies for C-Cl were observed at 772.63 cm-1 (most intense signal), 931.88 cm-1, and 1368.95 cm-1. For the hydrogenated form, these were at 776.85 cm-1 (most intense signal), 930.30 cm-1, and 1373.41 cm-1. The general trend is that the frequency for the same stretch in the monohydrogenated form is slightly higher than that of the original molecule. Opposite is a 3D representation of the monohydrogenated product, having had its geometry optimised by the density-functional molecular orbital method.

Pentahelicene

References

  1. ↑ A. Schulz & L. Flood, J. Org. Chem., 1986, 51, 838-841
  2. ↑ S. Leleu et al., Tetrahedron, 2004, 15, 3919-3928
  3. ↑ S. Elmore & L. Paquette, Tetrahedron Letters, 1991, 32, 319-322
  4. ↑ W. Maier & P. Shleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900
  5. ↑ A. McEwen & P. Schleyer, J. Am. Chem. Soc., 1986, 108, 3951-3960
  6. ↑ A. Greenberg, D. Moore, & T. DuBois, J. Am. Chem. Soc., 1996, 118, 8658-8668
  7. ↑ N. Fernandes et al., J. Org. Chem., 2008, 73, 6413-6416
  8. ↑ H.Rzepa et al., J. Chem. Dalton Trans., 1992, 447-450
  9. ↑ http://www.ch.ic.ac.uk/local/organic/mod/mo_4.html
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:s_j_hines_org&oldid=820712"