Rep:Mod:s j hines inorg

Computational Inorganic Chemistry Laboratory

Introduction

In this laboratory, a variety of computational techniques were used in order to structurally and energetically optimise, and analyse characteristics of, a number of molecules. At first, simple factors were found and compared:

1. Bond Lengths
2. [ http://en.wikipedia.org/wiki/Molecular_geometry Bond Angles]
3. Final Energy for the Molecule
4. Dipole Moments
5. Point Groups

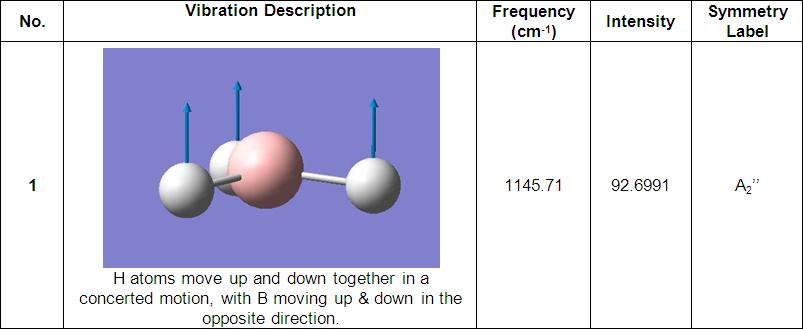
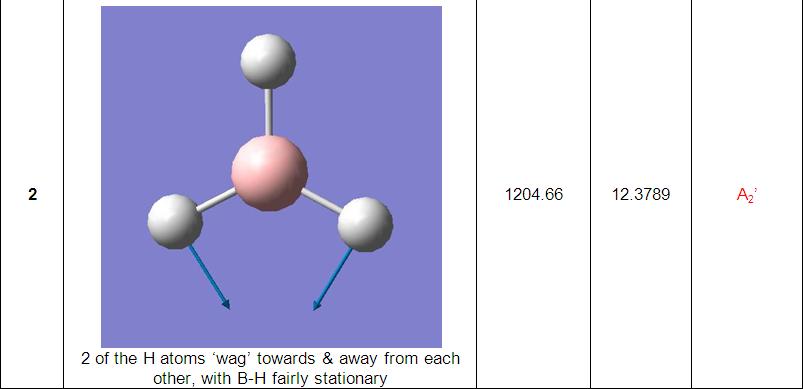
Further investigation saw the vibrations of particular molecules calculated and compared with each other and to literature/experimental values.

Semi-empirical Molecular Orbital Theory was the method used for the optimisation of energy and structure. For analysis of the molecules, BH₃, BCl₃, SiH₄, and Mo(CO)₄(PMe₃)₂, it was the common density-functional B3LYP Hamiltonian that was used in the calculation. This method and another were used to examine ammonia and comparisons were made between the two and the effects of using each method of optimisation were investigated. This is the MP2 method. It is based on 'Moller-Plesset Theories', it is known to be more reliable than the above density-functional method. Along with investigating the effects of different calculations, another factor is symmetry of the molecule and how this affects the optimisation. This was also considered, with respect to ammonia.

For all of the above calculations, values evolved from these were compared to literature values (where appropriate and available).

Calculations in this laboratory were examined in the 'GaussView' interface, having used the 'Gaussian' program to perform them.

The BH3 Molecule The BH3 molecule was optimised using the B3LYP method with the 3-21G basis set. This produced the following information: • Calculation type ‘FOPT’ • File type ‘.log’ • B-H bond length of 1.19435 Å • H-B-H bond angle of 119.99998 ° • Final energy of -26.462226438 a.u. • Dipole moment of 0 Debye • D3h Point Group • Calculation time of 28.0 seconds • Coordinates of atoms in the molecule (in angstroms): Boron at (0.000000, 0.000000, 0.000000), with Hydrogens at (0.000000, 1.194353, 0.000000), (1.034340, -0.597176, 0.000000) and (-1.034340, -0.597176, 0.000000). Pentahelicene Due to reasons discussed in the introduction, optimisation calculations made with a particular Hamiltonian and a particular basis set on a molecule cannot be compared with any accuracy or validity to a calculation made via a different method of optimisation. For this reason, exactly the same method/basis set was used to optimise two further molecules to allow comparison. This, and the results for these two molecules (BCl3 and SiH4) are shown in below sections. 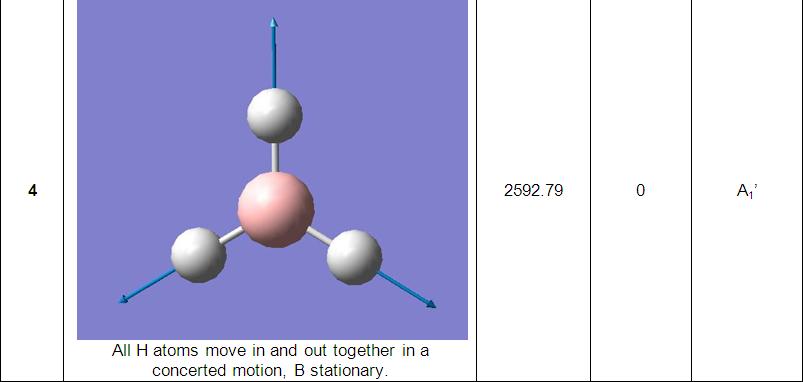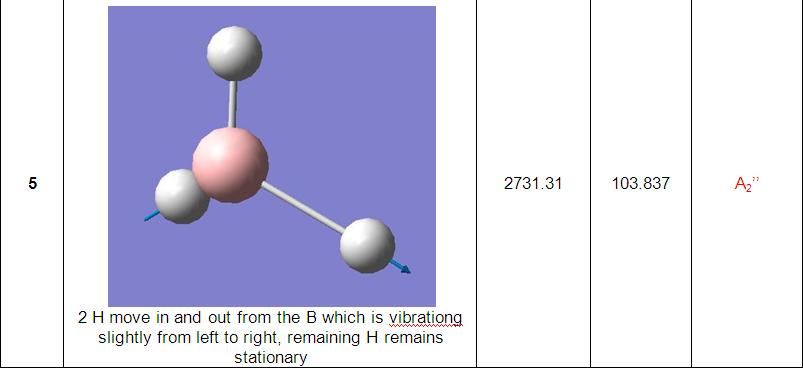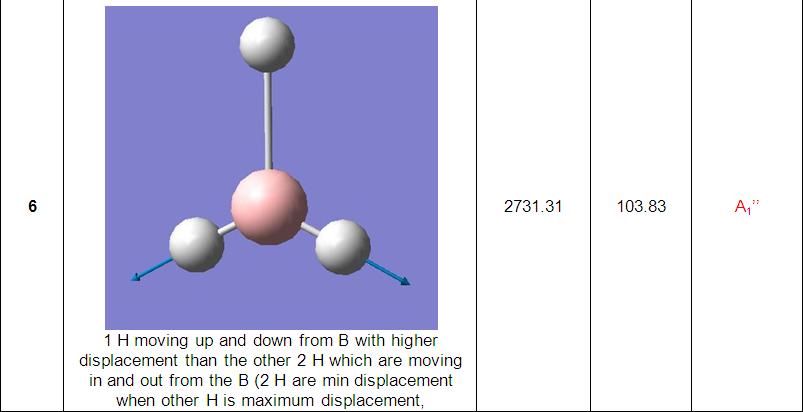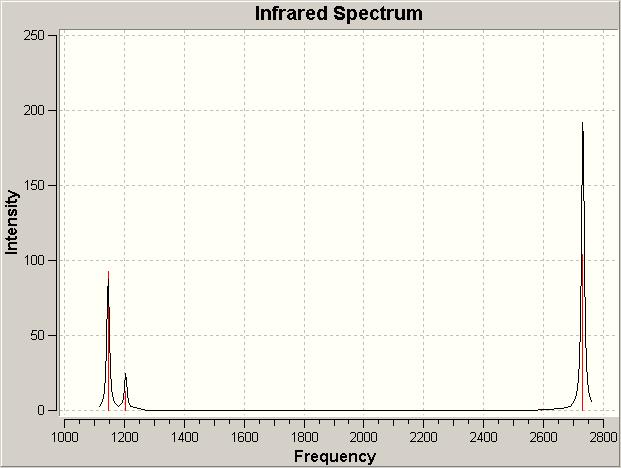Once this simple information had been recorded, further analysis of the BH3 molecule was carried out – to make a prediction of the vibrations that occur within this molecule. This calculation was performed, and the yielded 6 signals, corresponding to 6 different vibrations in the molecule. The information is summarised in the table pictured below. The nature of the vibration is described, a pictorial representation of each vibration is shown, the frequency at which it occurs, the intensity of the peak, and finally the symmetry label of the vibration within the D3h point group. The calculation of vibrations of this molecule also allowed a predicted infrared spectrum to be constructed. This is what is pictured below the information table. It is clear that there are 6 vibrations within the BH3 molecule, but there is less than 6 peaks seen on the spectrum - it actually shows three peaks. By examining the table, it is possible to see that out of the 6 different vibrations, there are 2 groups of 2 that have the same frequency of vibration. Therefore, a peak at these two values is actually two peaks superimposed on to each other. The final part of the investigation of the BH3 molecule involved calculation and examination of its molecular orbitals. Before these were calculated using the ‘Gaussian’ program, a molecular orbital diagram was constructed using 'ChemDraw' program (pictured below). 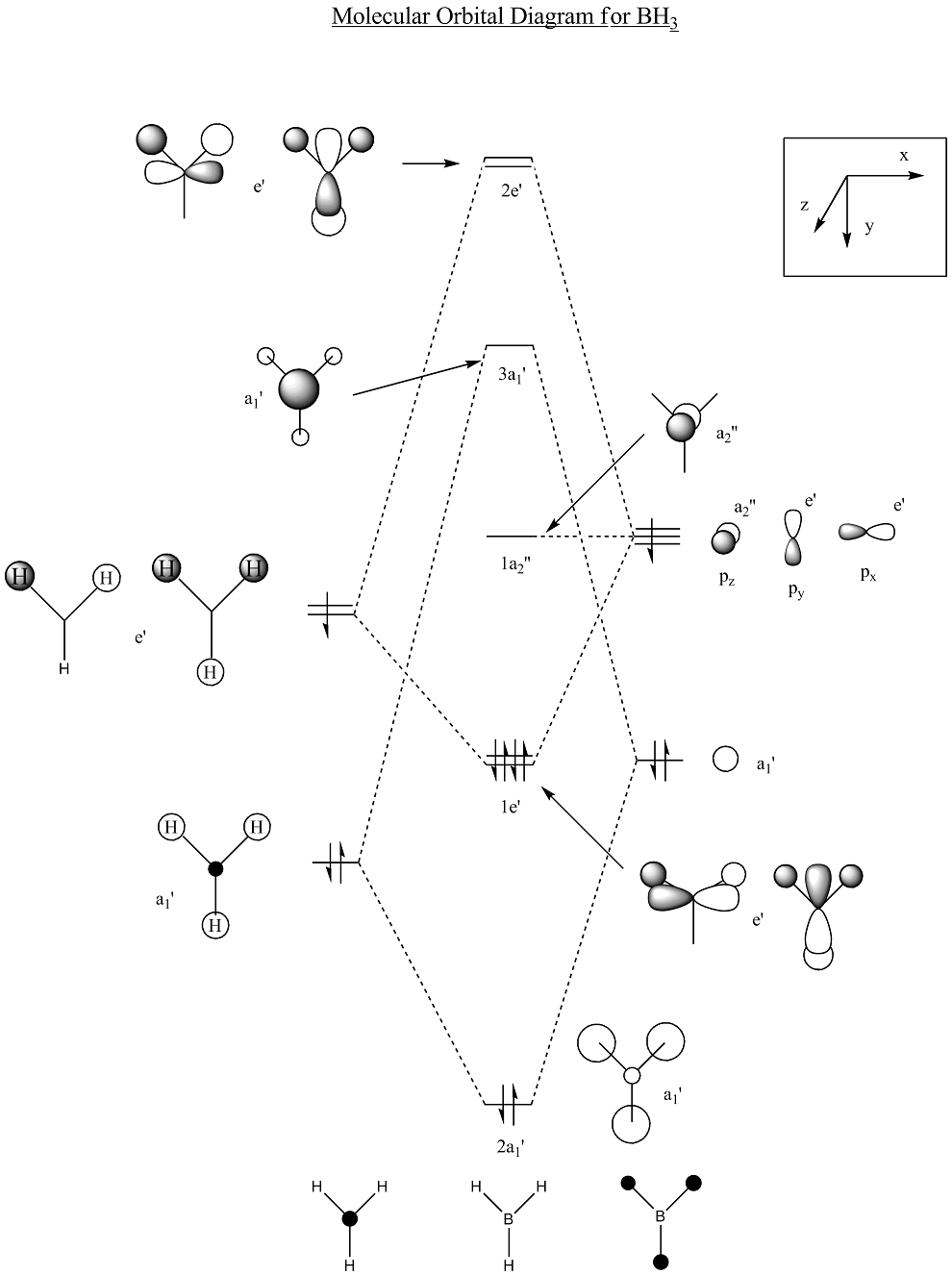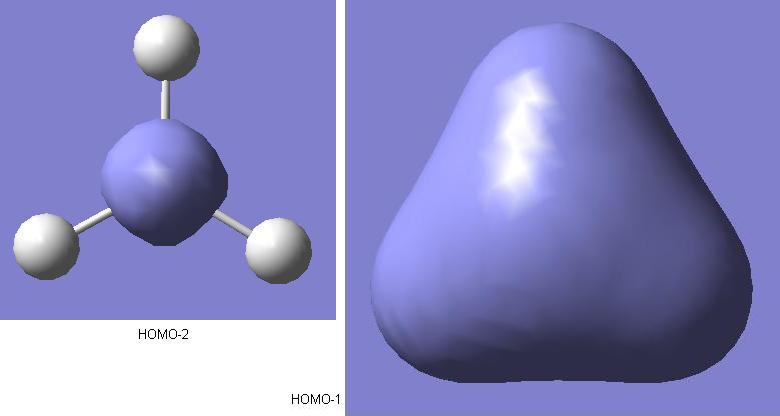After the molecular orbital diagram above was completed, a calculation was performed in order to get an idea of what these molecular orbitals shown in it actually look like. This would then allow comparison to the qualitative prediction made through the method above, and to assess its validity, accuracy and effectiveness. As shown above, these are the calculated predicted molecular orbitals for the HOMO-2 and HOMO-1 levels. For the bonding in this borane molecular orbital diagram, it is the 2s and 2p levels of the boron atom that are taking part. The HOMO-2 level molecular orbital is the non-bonding boron 1s level. The reason that it is not shown on the diagram is that it too low in energy for interaction with the hydrogen 1s orbitals, so will not effect the bonding. The first molecular orbital on the diagram is the HOMO-1. There is a clear resemblance between this qualitative prediction from the MO diagram and the quantitive prediction from the calculation. Early indications show that for this simple BH3 molecule, the qualitative MO analysis in the diagram is useful for giving an idea as to the form of the real molecular orbitals. There are two degenerate molecular orbitals at the [http://en.wikipedia.org/wiki/HOMO HOMO level shown above here. These again show good alignment with what was expected in the MO diagram. However, the limited nature of the method of calculation is demonstrated as well. The two HOMO level degenerate molecular orbitals shown here exhibit imperfect symmetry, which obviously is not expected. If a more time consuming, accurate method with a larger basis set were used for the molecular orbitals calculations, then we would expect the molecular orbitals to be showing the appropriate σ symmetry to a greater degree of accuracy. Comparing the qualitative LUMO from the diagram and the above quantitive prediction from the calculation, they're exactly the same as each other. Construction of the MO diagram is a very good method for predicting simple orbitals such as this, but gives a slightly more vague idea of molecular orbitals that are a little more complicated. Examples of this case would be comparison between the below 2 LUMO+1 level molecular orbitals, and the ones predicted in the diagram. Although these are still easily assigned to the ones in the diagram, the more complicated the molecular orbitals become, the more difficult it becomes to visualise the real molecular orbitals to the qualitative predicted ones.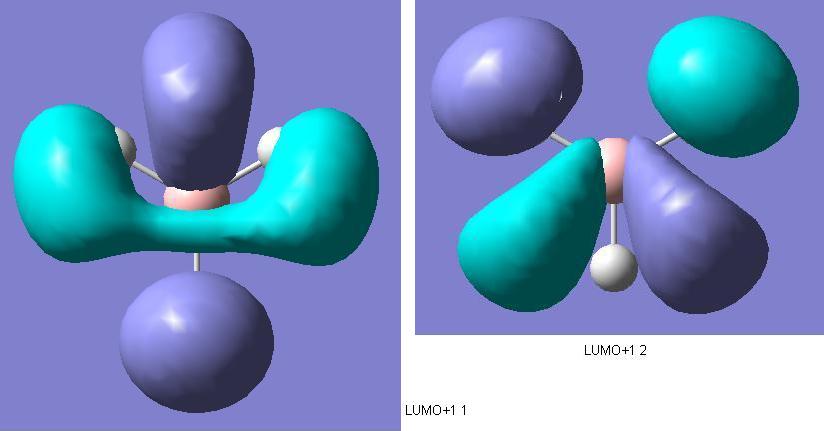

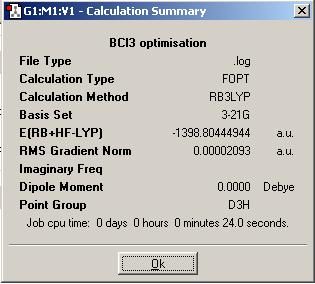
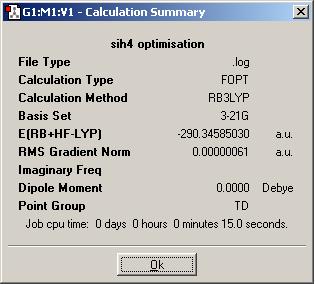
The BCl3 Molecule The BCl3 molecule was also optimised using the B3LYP method with the 3-21G basis set. This produced the following information: • B-H bond length of 1.77504 Å • H-B-H bond angle of 120.0002 ° • Coordinates of atoms in the molecule (in angstroms): Boron at (0.000000, 0.000000, 0.000000), with Chlorines at (0.000000, 1.775043, 0.000000), (1.537232, -0.887522, 0.000000) and (-1.537232, -0.887522, 0.000000). Pentahelicene The SiH4 Molecule Similar basic calculations that were carried out for the BH3 molecule above were performed on another molecule: SiH4. It was optimised (DOI:10042/to-1332 ) using the B3LYP method with the 3-21G basis set - exactly the same method as with the borane. As discussed previously, this has to be the case to allow comparison between the values evolved from the calculation for each molecule to be accurate/valid. This produced the following information: • Si-H bond length of 1.49590 Å • H-Si-H bond angle of 109.47122 ° • Coordinates of atoms in the molecule (angstroms): Silicon at (0.000000, 0.000000, 0.000000), with Hydrogens at (0.863659, 0.863659, 0.863659), (-0.863659, -0.863659, 0.863659), (-0.863659, 0.863659, -0.863659) and (0.863659, -0.863659, -0.863659). Pentahelicene

Isomers of the Mo(CO)4L2 Molecule Pentahelicene Pentahelicene The first part of this section involved the optimisation of the cis (DOI:10042/to-1299 ) and trans (DOI:10042/to-1301 ) isomers of the complex where L = P(Me3)2. Due to this molecule being a lot more complicated than the molecules previously considered in this laboratory, obviously higher level and more intensive/time consuming. For this reason, the calculation was carried out in a number of separate steps. After the molecule was constructed using the molecule builder, the first step was to optimise this using the B3LYP method and a pseudo-potential/basis set 'LANL2-MB' (the 'convergence criteria' were also set to 'loose'). The resulting molecule from the first step was immediately re-optimised, this time using the same method but using the alternative pseudo-potential/basis set 'LANL2-DZ' and setting the 'electronic convergence' to 'ultra fine'. The final step was to make sure that the tendency of the phosphorus atom to become 'hypervalent' was considered (due to low-lying d-orbitals). So far, only s- and p-orbital functions had been considered. This justified a final optimisation by the 'B3LYP/LANL2-MB' method, this time including d-orbital functions. Once this had been completed, this yielded an optimised geometry of the molecule. This was carried out for both isomer, and the result of this optimisation are shown in the 3D representations left. The two isomers are similar in energy, the difference in energy between them is 0.00076730 a.u. (2.015 kJ/mol), with the trans isomer more stable due to it being lower in energy. The bond lengths for Mo-C and Mo-P are longer in the cis isomer than they are in the trans isomer. Trans: 2.02869 , and 2.52471 respectively, whilst cis: 2.03199 , and 2.5891 respectively. Shorter bonds means stronger bonds, thus the trans isomer is more stable overall. Sometimes it is necessary to alter the ligands of a complex in order to stabilise the isomer that provides most use e.g. as a catalyst. It has been found that the trans isomer of the complex examined in this section is the most stable. However if it is the cis isomer that is most the most useful in catalysis, then the phosphorus-based ligands need to be altered to make sure the cis isomer is produced. An efficient way to ensure that the phosphorus ligands are cis to each other in the complex, is to insert a bridge between the two phosphorus atoms, 'locking' them in place. The vibrations and infrared spectra of both of the isomers of the complex were computed using the fully optimised structures as described. The predicted infrared spectra of the cis (DOI:10042/to-1306 ) and trans (DOI:10042/to-1305 ) isomers respectively are pictured below. There were four vibrations for CO found for each complex. For the cis isomer these were at 1961.84 cm-1, 1873.75 cm-1, 1855.48 cm-1, and 1850.06 cm-1. For the trans isomer these were at 1958.28 cm-1, 1885.98 cm-1, 1843.07 cm-1, and 1842.45 cm-1. This is not what is expected for the trans isomer. The cis isomer was expected to have 4 absorption bands but the trans isomer was only expected to have 1. This gives an indication that the optimisation of the structure has not been carried out to a great enough degree of accuracy for accurate computation of the vibrations to be carried out. A literature (REFFF) example has been found to verify this expectation of different numbers of CO vibrations found within the different cis and trans isomers of a similar appropriate complex.

The Ammonia Molecule In this section, it was the ammonia molecule that was examined. Firstly, the effect of symmetry of the molecule on calculation was investigated. The ammonia molecule was optimised starting from three different symmetries to investigate how this alters the calculation. The B3LYP/6-31G method was used for this. Snapshots were taken of the 'summary' of each of the calculations, and are shown below. The 3D representation shown right is the C3v geometry optimised using the MP2/6-311+G(d,p) method. 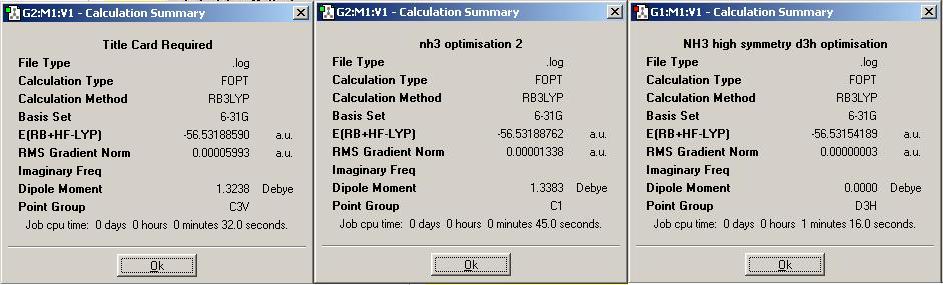Pentahelicene It can be seen that the starting symmetry does affect the final structure. It is possible to tell this from the different dipole moments that are shown. If the final structure obtained was exactly the same in each case, then the dipole moments should be exactly the same. The preferred configuration of ammonia, the molecule with C3v symmetry, has taken the least time to optimise (32.0 secs), and as the molecule moves away from this symmetry, the time for optimisation increases, as shown above, from 45.0 secs to 76.0 secs. The 'Gaussian' program optimises the molecule for the symmetry given to the molecule in the input file. Symmetry will not break in the optimisation unless it is specifically set for the program to 'ignore' this factor. If a high symmetry structure needs to be analysed, the fact that symmetry breaking cannot take place causes the calculation time to be much slower. According to this optimisation, the C1 geometry has the lowest energy. This makes the difference in energy between the highest (D3h) and next lowest (C3v), 0.00034401 a.u. The energy difference corresponds to the energy barrier of inversion => 0.903 kJ/mol. 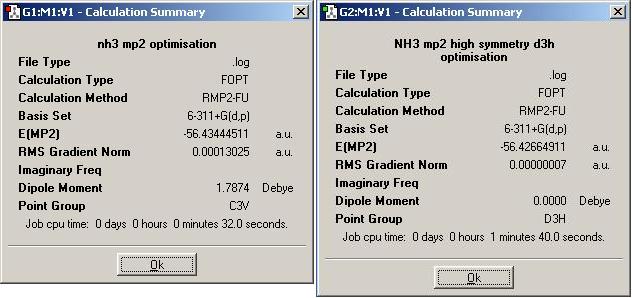Secondly, the ammonia molecule was optimised using a more accurate method in order to find out what effect this had on the calculation. The method used was 'MP2/6-311G+(d,p)'. The pre-optimised molecules of the C3v and D3h geometries from above were used for the starting point of this calculation. Snapshots were taken of the 'summary' of each calculation and are shown below. From the summary snapshot, the time for the optimisation calculation the C3v geometry can be seen as the same for the second method as the simpler first method. However, considering the calculation was carried out on the pre-optimised molecule, the time for calculation has actually increased for the second, more intense calculation. The same is true for the D3h geometry; although it has increased compared to the time for the first, this increase is larger than seen due to the same reasons. The difference in energies between these two geometries is again the barrier energy of inversion. In this case this energy is 0.007796 a.u. The energy calculated here is much higher than the energy calculated for the same factor in the first calculation, but as this is a much more accurate method, it shows good correlation with the experimental value of 24.3 kJ/mol - this difference in energy equates to 20.899 kJ/mol. With the optimised structure found using the MP2/6-311G+(d,p) method above, the vibrations of the ammonia molecule were computed for each geometry. The results are tabulated below. It is seen that there are all positive frequency values for the C3v geometry because it is the ground state configuration. For the D3h geometry, there is 1 negative frequency of -318.051 cm-1, providing evidence that it is indeed the inversion transition configuration as expected. Vibrations in the table with corresponding numbers between each geometry have the same 'character of motion'. The vibrations were visualised, and one was found to follow the same path as the inversion of the molecule. In each case that was vibration 1 shown in the tables. 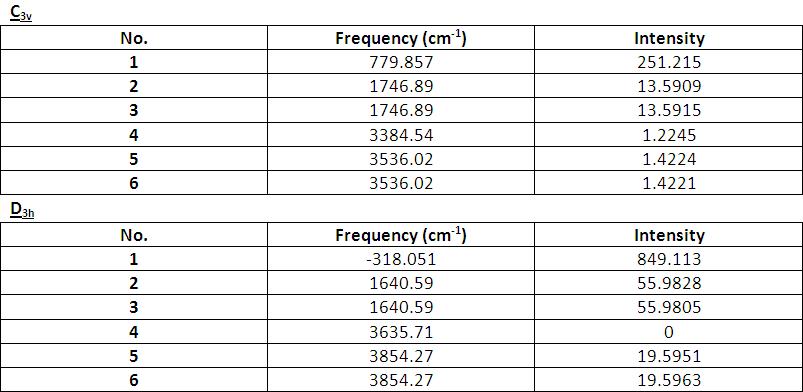References