Rep:Mod:rvirdee3
3rd Year Computational Lab Module 3:
Transition States
Introduction
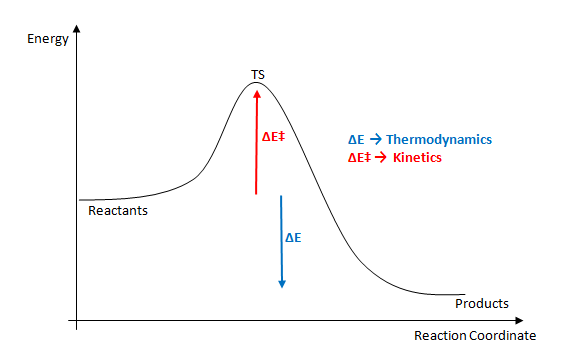
In the first two modules we have solely looked at chemical reactions via the thermodynamics. That is to say, we have only analysed reaction via the energies of the reactant molecules, and the products. In this module however, we shall firstly learn how to find the transition states of simple reactions, and then, look at the energies of these transition states. The energy of a transistion state, and its energy with respect ot the reactants gives us an indication of the kinetics of the reaction. The difference between the energy of the reactant and the transition state is the activation energy of the reaction.
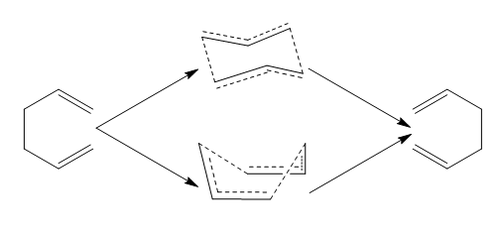
In this module of the lab course, we shall investigate a [3,3] sigmatropic shift in the form of the Cope Rearrangement, and two different Diels Alder Reactions: The reaction between cis-Butadiene and ethylene; and the reaction between 1,3-cyclohexadiene and maleic anhydride. These relatively simple reactions will not be too demanding computationally and are relatively easy to investigate. In the case of the Cope rearrangement, we shall investigate the two possible transition states of the reaction (chair and boat) and how their energy influences which process occurs. In the first case of Diels Alder reaction, there is only one transition state, and we shall use it to help gain some simple understanding of the orbitals involved in the concerted cycloaddition reaction. Then, we shall move onto a more complex case, and investigate the energies of the exo- and endo- transition states, and how their energies dictate which product predominates under real reactions.
The Cope Rearrangement Tutorial
The Cope Rearrangement involves the [3,3] sigmatropic rearrangement of 1,5 dienes. The reaction was developed by Arthur Cope in the 1930-40s and has been shown to be a purely intramolecular process[1]. Over the years, there has been much discussion over the possible mechanisms involved in the reaction, concerted, stepwise and dissociative mechanisms have all been proposed, however, it is now widely accepted that the reaction does go via a concerted mechanism. In this part of the module, we will investigate the Cope Rearrangement of 1,5-hexadiene, a system which has previously been studied computationally, showing a good agreement with experimentally determined values. We can imagine that the transition state of the reaction (which will have no carbon-carbon double bonds) will be similar to cyclohexane, and therefore, we could possibly observe transition states in both the boat and chair conformations. Both of these cases shall be investigated.

Optimisation of Reactants and Products:
In the case of the Cope rearrangement we are going to study (that of 1,5-hexadiene), the products and reactants are the same. Therefore, we only need to do one set of calculations for these. We know that there are numerous possible conformations of this molecule, therefore, we will need to decide which is the most stable (and therefore the most abundant conformer), and which will result in the Cope Rearrangement occurring.
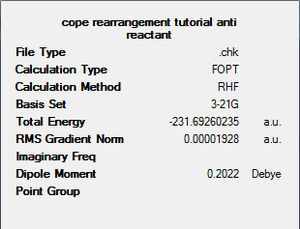
Anti Conformation 1:
The first conformation to be investigated was an anti- conformation, with an anti-periplanar C-C linkage at the central bond. The molecule was drawn in GaussView and then an optimisation calculation was set up. The calculation was set up with the HF/3-21G level of theory, using Hartree-Fock as the method, with the 3-21G basis set. The memory used in the calculation was set to 250MB (to prevent severe error #2070). The energy of the resulting structure was recorded, as was the symmetry.
| Structure |  |
 |
|---|---|---|
Gauche Conformation 1:
The next conformation to be investigated is a Gauche conformation (Gauche linkage between central 4 carbon atoms). Conventionally, we expect that Gauche conformations are higher in energy than anti-periplanar ones due to steric effects. As the case was above with the anti conformation, we set up an optimisation calculation with the molecule drawn using a HF/3-21G level of theory. That was, we can compare the energies of the two conformations drawn. The energy of the conformation was noted, as was the symmetry. A comparison between the energies of the two conformation was also made, so observe which is the more stable.
| Structure | 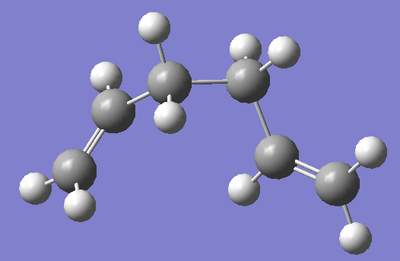 |
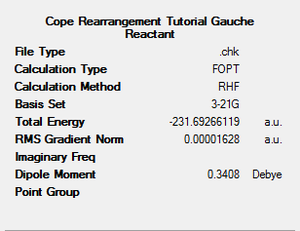 |
|---|---|---|
As we can see, the Gauche conformation is in fact lower in energy than tha Anti conformation. This is not what we would have expected. This is most probably due to attractive Van der Waals forces between the groups bound to the central C-C unit in the molecule. As this conformation is lower in energy than the Anti-1 reactant shown above, we can assume that it would be a more abundant conformation in the reaction mixture.
Gauche Conformation 2 (High Energy):
By complete accident, the most stable Gauche conformation was drawn above. Therefore, for the sake of comparison, the higherst energy Gauche Conformation shall be drawn. This will show that the particular Gauche Conformation above is particularly stable, whereas the majority of Gauche Conformations are in fact higher in energy than the Anti conformations. Again, the molecule was drawn in GaussView, and optimised to a HF/3-21G level of theory so that the results from the calculation could be fairly compared to those conformations above. The data for the absolute energy, the relative energy of this conformation with respect to both the Anti-1 and Gauche conformation above and the symmetry point group of the conformation were recorded.
| Structure | 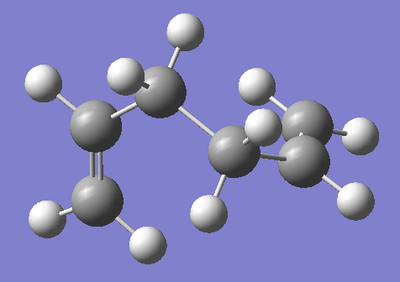 |
 |
|---|---|---|
The data above shows that this Gauche conformation of the molecule is significantly higher in energy than the previous two examples. This goes some way to showing how it is not a rule that Gauche reactants are more stable than Anti ones, in fact it is the opposite that is generally true. However, the case of the Gauche-1 conformation is just an exception.
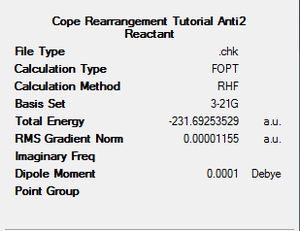
Anti Conformation 2 (Ci symmetry):
It has been shown that the Cope Rearrangement does not occur from any of these conformations of 1,5-hexadiene. The reaction actually occurs via another Anti conformation, one slightly higher in energy, but that has the correct alignment of fragments to allow the reaction to occur. The molecule was drawn in GaussView and again optimised to a HF/3-21G level of theory. The energy of the molecule was recorded, as was its symmetry point group.
| Structure | 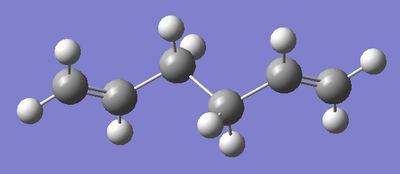 |
 |
|---|---|---|
As discussed above, it is this conformation of the 1,5-hexadiene that undergoes the Cope Rearrangement, so, from now on, we shall use this form of the reactant.
DFT Optimisation of Anti Conformation 2 (Ci symmetry):
We can use the HF/3-21G level of theory in calculations for a crude approximation of energies. However, if we want a better indication of energy of the molecules, we must go to a higher level of theory. As both the reactants and products only contain carboon and hydrogen, we do not have to use a very complicated basis set or calculation type. Therefore, once the Anti conformation with Ci symmetry was optimised to a HF/3-21G level of theory, we set up a DFT calculation with a B3LYP/6-31G (d) level of theory. This will ensure we get a better representation of the energy of the molecule for further comparison. The results are given below.
| Structure |  |
 |
|---|---|---|
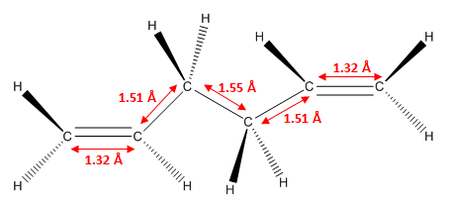
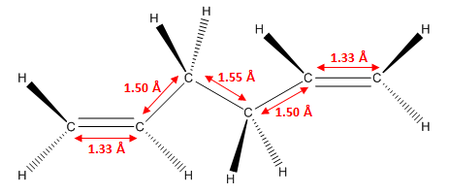
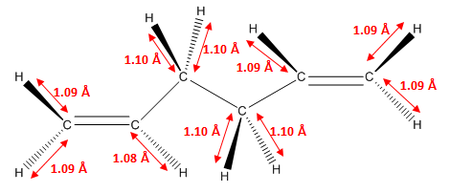
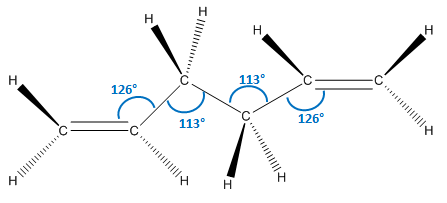
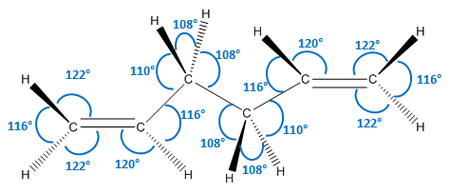
As we can see, the two levels of theory give quite different energies for the molecule. However, as we are using different types of calculations with different levels of theory, we cannot compare the energies of the molecules between the two. However, we can compare geometric parameters, such as bond lengths and bond angles. These are shown below.
| Parameter | HF/3-21G | DFT B3LYP/6-31G (d) |
|---|---|---|
 |
 | |
 |
 | |
 |
 | |
 |
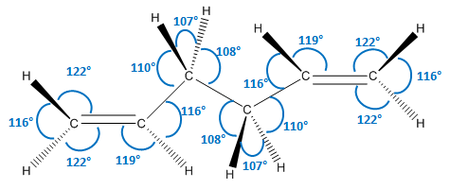 |
As we can see from the data above, there is no significant change in any of the geometric parameters of the two structures once optimised with the different methods. We would not expect a large change. However, there are some notable differences:
- C=C bond lengths are larger in DFT than in HF optimised structure
- C-C bond lengths are smaller in DFT than in HF optimised structure
- C-H bond lengths are larger in DFT than in HF optimised structure
- All bond angles generally stay the same
Frequency Calculation of DFT Optimised Structure:
To observe whether or not we have reached the true ground state of the conformation, we can use the technique of frequency analysis. The first thing to look for is the "low frequencies" of the vibrations. The largest low frequency (11.1923 cm-1) is almost 1 order of magnitude larger than the lowest normal vibration (73.8746 cm-1), thus, we have one indication that we have reached the ground state. We can also look for negative frequencies in the output. The Vibrational Spectrum of the molecule is shown below.

As we can see, there are no negative frequencies to report, therefore, we can say that the optimisation has in fact taken us to a ground state configuration of the anti-2 conformation of 1,2-hexadiene.
Using the data from the frequency calculation, we can also get more useful values for the energy of the molecule. The absolute energy of the molecule that is given in GaussView is the purely electronic energy, i.e. the energy of the molecule at 0 K. This is not the most useful indication of the energy, as all experimental data will be recorded at closer to room temperature. The output .log file of the calculation gives us numerous other measures of the energy which are more useful to us in real life. The 4 energies listed in the output that we are interested in are:
- Sum of electronic and zero point energies: Potential energy at 0 K including zero point vibrational energy.
- Sum of electronic and thermal energies: Potential energy at 298.15 K and 1 atm of Pressure including contributions from translational, rotational and vibrational modes at this temperature.
- Sum of electronic and thermal enthalpies: Same as above, but includes +RT correction term.
- Sum of electronic and thermal free energies: Same as Sum of electronic and thermal energy but includes entropic contribution to free energy.
These values and the value of the electronic energy are given below.
| Electronic Energy (amu) | Sum of electronic and zero point energies (amu) | Sum of electronic and thermal energies (amu) | Sum of electronic and thermal enthalpies (amu) | Sum of electronic and thermal free energies (amu) |
|---|---|---|---|---|
Finding the Transition States:
Now we have found and optimised the conformation of 1,5-hexadiene, our attention now turns to finding the transition state of the Cope Rearrangement. As discussed above, we expect to observe two different transition states, one with a chair-like structure and one with a boat-like structure (analogous to conformations of cyclohexane). First, we shall find the chair transition state of the Cope Rearrangement. There are two different techniques that can be used to do this, and we shall investigate both. Hopefully, we shall obtain identical structures via the two apporaches.
Chair Transition State via Calculating Force Constant Matrix:
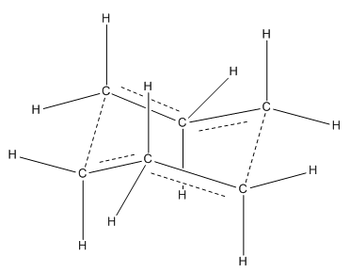
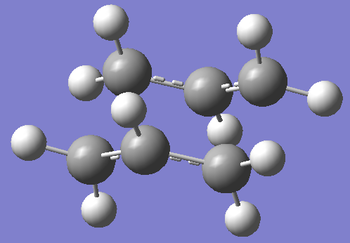
The first way we can find the transition state is by using the Force Constant Matrix. If our starting geometry of the molecule is close enough to that of the transition state, we can let the calculation compute the force constant matrix at the first step. This will let the calculation know which direction results in a negative curvature of the potential energy surface, therefore, facilitating the finding of the transition state. To begin with, an allyl fragment (CH2CHCH2) were drawn in GaussView. This was then optimised to a HF/3-21G level of theory to give the lowest energy structure. Once optimised, the structure was copied twice into a new molgroup, with the fragments eclipsing each other fully, with an inter-fragment distance of 2.2 Å. Once this was done, an opt+freq calculation was set up, with optimisation to TS (Berny). The calculation was set up to compute the force constant once, and te keywords "opt=NoEigen" were used to stop the calculation from crashing if more than one negative frequency was calculated. Once the job was submitted, and the output was opened, we observed the transition state of the Cope Rearrangement via a Chair Transition State. The molecule's identity as a transition state was confirmed by the presence of a vibration with a negative frequency with magnitude 818 cm-1.
| Schematic of Transition State | Calculated Transition State | Vibration Causing Reaction |
|---|---|---|
 |
 |
 |
As we can see from the pictures above, the vibration at -818cm-1 is causing the reaction to occur. We observe two of the terminal carbon atoms moving closer together (representing the formation of the bond) and the other two moving apart (representing the braking of a bond). We also observe the movement of the central carbon atoms towards the terminal carbons that move apart. This represents the movement of the carbon carbon double bonds across the molecule.
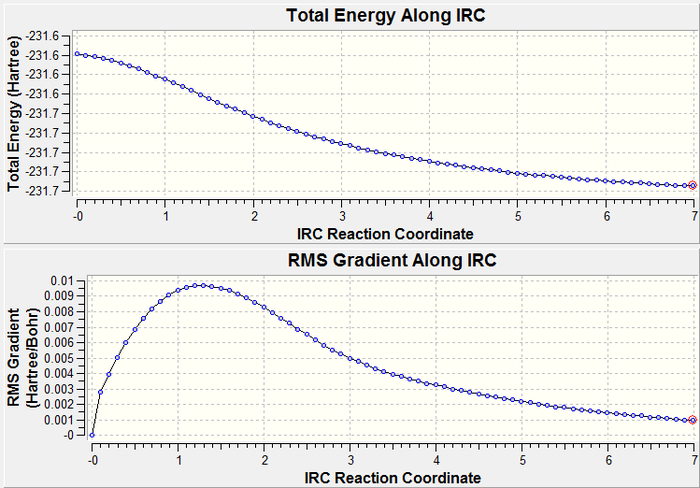
Once the transition state had been found, we set up an IRC calculation to look at the progress of the reaction. IRC (Intrinsic Reaction Coordinate) creates a series of steps from the transition states following the direction in which the gradient of the energy surface is maximum. In this case, this corresponds to the progress of the reaction from the transition state to the final product. As the transition state had been optimised to a HF/3-21G level of theory, the same level was used for the IRC calculation. The force constants were read once and the number of steps was set to 70 to ensure the full transformation could occur. As the movement from the transition state to the reactants and products is the same (i.e. symmetric) we can set up the calculation to only progress forwards, as we know the geometries and energies will be identical for movement towards the product or reactant molecule. Below is shown the form of the molecule at the first and last steps of the calculation, and a plot of the energy and gradient across the calculation. The molecule at the first stage at the IRC calculation corresponds to the transition state, and the last step shows the product of the Cope Rearrangement.
| Steps of IRC Calculation | Progress of IRC Calculation | |
|---|---|---|
 |
 | |
 | ||
Chair Transition State via Freezing Coordinates:
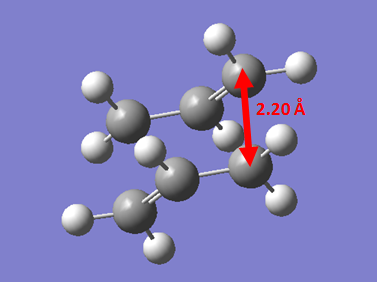
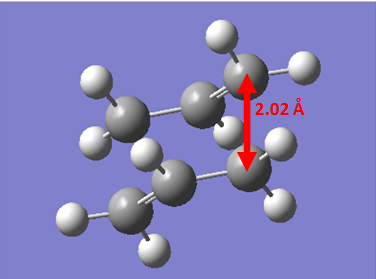
Once the Chair Transition State had been found via an optimisation approach using two fragments resembling the transition state, we investigated another way of finding the Transition State. A new molgroup was set up and the two guess fragments were copied into the box. The, using the Redundant Coordinate Editor, the terminal carbons of the allyl fragments were frozen with the settings of bond and freeze coordinate with a distance between the fragments of 2.2 Å. Then, a normal optimisation calculation was set up and it was noticed that the keywords "opt=ModRedundant" had been included. A HF/3-21G level of theory was used, and the calculation was submitted. Once the calculation had finished, we observed a structure similar to the chair transition state found above, however, the bond making/breaking distance was still set to 2.2Å. This length was then optimised by using the Redundant Coordinate Editor on these lengths, and setting it to bond and derivative. The calculation was then sent, and the output had the fully optimised chair transition state.
| Before Optimisation of Inter-fragment Distance | Before Optimisation of Inter-fragment Distance |
|---|---|
 |
 |
The two structures for the transition states found using either approach were to all intents and purposes identical. The energies of the two forms are given below so a comparison of how similar they really care can be made.
| Method for Finding Transition State | Force Constant Matrix | Freezing Coordinates |
|---|---|---|
As we can see, the two approaches give us optimisations to transition states with the same energy, which is what we would have expected, but it is always worth checking to ensure no mistake has been made with the calculation. The first method (Force Constant Matix) is the best option if you know the general geometry of the transition state you are looking for, and if it can be easily drawn in GaussView. If this is not the case, we can use the case of frozen coordinates to aid us in finding the transition state if we know the geometry of the product.
Boat Transition State via QST2 Calculation:
To find the boat transition state of the Cope Rearrangement, we have to use yet another technique, using a QST2 calculation. In this style of calculation, one draws the reactant and product molecule in the same molgroup (but in different windows within the group) and the calculation will linearly interpolate between the reactant and product to find the transition state. To ensure this occurred, the labels on the all of the atoms in the reactant must correspond to the final position of those atoms in the products as it is via the labels that the calculation will differentiate between atoms in the structure.
| Starting Geometry for QST2 Calculation | Final Geometry for QST2 Calculation |
|---|---|
 |
 |
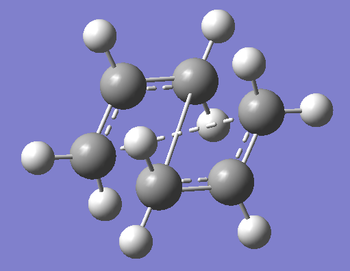
Using these geometries, the calculation was set up using Optimisation to TS (QST2), using the HF/3-21G level of theory. The calculation was submitted and the outcome is what is shown below.
| Schematic of Transition State | Calculated Transition State | Vibration Causing Reaction |
|---|---|---|
 |
 |
 |
As we can see, this is clearly not the correct structure for the transition state. The QST2 calculation will generate the transition state purely by the linear movement of atoms and groups, it will not take into account the rotation of groups about a bond. For the sake of completeness, I ran the IRC calculation for the wrong boat transition state just to see what the results were like.
| Steps of IRC Calculation | Progress of IRC Calculation | |
|---|---|---|
 |
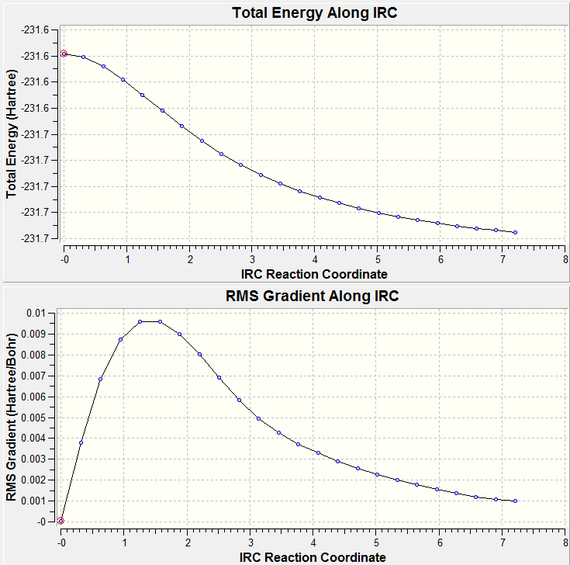 | |
 | ||
The IRC for the reaction from the boat transition state indicates that the programme truly believes that this reaction could occur via this transition state. As stated above, we can dismiss this as a structure as a possible transition state, as the reaction could not occur in this fashion. Therefore, we need to help the calculation by putting the original structure in a conformation closer to the boat transition state. As we are using a QST2 calculation, we need to do this for both the product and reactant molecule, with the labels of the atoms corresponding to where they would move from the reactant to the product.
| Starting Geometry for QST2 Calculation | Final Geometry for QST2 Calculation |
|---|---|
 |
 |
The QST2 calculation was set up, once again using HF/3-21G level of theory, resulting in the correct boat transition state being found. The structure of the found transition state is shown below, with a schematic of the vibration causing the reaction and the energy of the transition state.
| Schematic of Transition State | Calculated Transition State | Vibration Causing Reaction |
|---|---|---|
 |
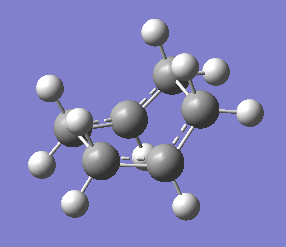 |
 |
For the correct boat transition state, I ran an IRC calculation to monitor the progression of the reaction away from the transition state to the products. As the reaction is symmetric, the calculation was set to run in the forwards direction only. The result of the calculation showing the starting molecule, the final molecule, and the progress of the reaction is shown below.
| Steps of IRC Calculation | Progress of IRC Calculation | |
|---|---|---|
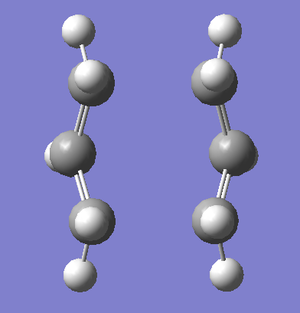 |
 | |
 | ||
As we can see from the energy plot and the derivative of the energy, the molecule becomes more and more stable as we move away from the transition state and towards the product molecule, which is obviously as expected. We shall now move on to look more carefully at the energies of the transition states and their implications on the Cope Rearrangement.
Calculating the Activation Energies of the Cope Rearrangement:
Now we have found both the chair and boat transition states for the Cope rearrangement. Using this information, we can go on to look at the activation energy of the reaction via these two transition states. To do this however, we need to use a higher level of theory to give a more accurate depiction of the transition states, and a better approximation of their energy. Above, we used a HF/3-21G level of theory to find the transition states. Now they have been found, I shall optimise them to a DFT B3LYP/6-31G (d) level of theory. That way, we can compare the energies of the transition states with the optimised version of the lowest energy reactant/product molecule found at the beginning of the module.
DFT Optimisation of Chair Transition State:
Using the transition state from the HF/3-21G level of theory, we set up another optimisation to transition state, this time using the DFT B3LYP/6-31G (d) level of theory. This gave us a more accurate depiction of the chair transition state in terms of structure and energy, and also gave a radically different value for the wavenumber for the vibration representing the reaction. This data is given below.
As we can see, there is a surprisingly large difference in not just energy, but all of the other parameters measured of the transition state between the two levels of theory. Using the higher level of theory, we observe a shorter inter fragment difference, which implies a stronger attractive force between the two fragments. We also observe slightly weaker C-C bonds in the DFT calculation with a small bond angle. The most notable differences are however, the large discrepancies between the vibration and the overall energy of the molecule. We observe a difference in the wavenumbers of about 250 cm-1 which is extremely large. However, as we observe a smaller inter fragment distance, we would think that would imply a stronger attraction between the fragments. That would tell us that the vibration causing the reaction would occur at lower energies. We also see a more stable energy using the higher level of theory, however, strictly speaking, we cannot compare energies from different methods.
DFT Optimisation of Boat Transition State:
Just as the chair transition state structure was further optimised to a higher level of theory, the same reoptimisation of the boat transition state was also run. The results comparing the structures, energies and wavenumbers of vibrations of the boat transition states optimised to the two different levels of theory are shown below.
In the case for the boat transition state, we again see large differences in the parameters taken from the results from the optimisations using the two different levels of theory. At the higher level theory, we observe longer inter-fragment distances and C-C bond lengths, which indicate a weakening of the attractive forces between the fragments and the C-C bonds respectively. Again, we see a large difference in the wavenumber of the vibration of the reaction. However, in this case, we see the inter-fragment attraction decrease, but still observe a decrease in the wavenumber and therefore energy of the vibration, therefore, my initial hypothesis concerning the relationship between the inter-fragment distances and the wavenumber of vibration is wrong. Again, we also see a more stable energy (more negative) using the higher level of theory, but as we have used different calculation techniques, we cannot compare the energies.
Calculating the Activation Energies of the Cope Rearrangement:
Now we have optimised the reactant (and necessarily the product molecule) and the transition states to a high enough level of accuracy using the same calculation methods, we can go on to calculate the activation energy of the Cope Rearrangement via the chair and boat transition states respectively.
| Structure | DFT B3LYP/6-31G (d) | ||||
|---|---|---|---|---|---|
Now we have all the data for the three species of interest all optimised using the same level of theory, we can calculation the activation energy of reaction for the two transition states. Of most interest is comparing the Sum of Electronic and Zero Point Energy of the reactant and each of the transition states, as this will give us the activation energy at 0 K, the other is the Sum of Electronic and Thermal Energy of the reactant and each of the transition states, as this will give us the activation energy under standard conditions (298.15 K and 1 atm of pressure).
| Transition State | Activation Energy at 0 K (kJmol-1) | Activation Energy at 298.15 K (kJmol-1) | Experimental Activation Energy at 0 K (kJmol-1) |
|---|---|---|---|
As we can see from the numbers above, the activation energy for the Cope Rearrangement of 1,5-hexadiene is lower for the chair transition state than it is for the boat transition state. This is understandable, as the transition states are very similar to cyclohexane, and we know cyclohexane favours the chair conformer to minimise steric interactions. We also observe that increasing the temperature from 0 K to 298.15 K has a much larger effect on the activation energy for the reaction via the chair transition state (decreases by 3.7 kJmol-1) than it does for the reaction via the boat transition state (decreases by 2.6 kJmol-1). We can also see that the calculated activation energy for the reaction progressing via the chair transition state matches the experimental data much better than in the case of the boat transition state (chair: calc. is 2.4 kJmol-1 greater, boat: exp is 11.4 kJmol-1 greater). This could be due to the computational method not fully accounting for the steric effects destabilising the boat transition state, under-estimating them, therefore giving a lower energy for that transition state, resulting in a lower calculated activation energy.
Links to Calculation Output Files:
Transition States of Cycloaddition Reactions:
In the previous section of this module, we condsidered the simple intra-molecular process of a [3,3] Cope Rearrangement. Now however, we shall increase the complexity of the problem, and look at cycloaddition reactions. We shall consider two basic reactions, both [4+2] Cycloadditions, more specifically, Diels Alder reactions[2]. Instead of using full quantum methods in this section of the module (such as DFT type calculations), we shall use Semi-Empirical calculation types using AM1 methods. This way, we can easily visualise the fronteir orbitals involved in the reaction, and therefore, using their symmetries, gain an added understanding of the reaction pathways. The two cases we shall consider are
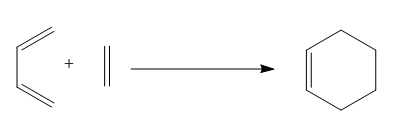
1. The simplest case of the Diels Alder Reaction between cis-Butadiene and ethylene[3].

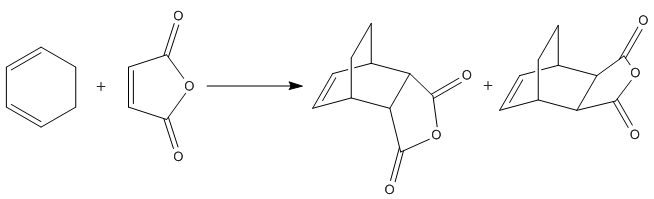
2. The more complex case of the Diels Alder Reaction between 1,3-Cyclohexadiene and Maleic Anhydride[4].

Diels Alder Reaction of cis-Butadiene and Ethylene:
The Diels Alder Reaction of cis-Butadiene and Ethylene is possibly the most simple reaction of this type that can be studied, as we are using the most simple diene (cis-Butadiene) and dienophile (Ethylene). We know that cycloaddition reactions are centred around the HOMO/LUMO orbitals of the reactants, so the first thing that needs to be studied is these orbitals.
AM1 Optimisation of cis-Butadiene:
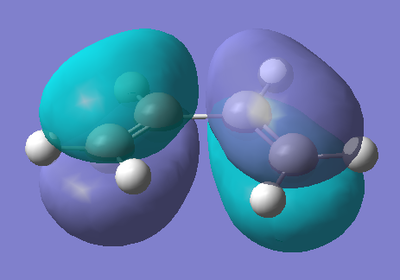
To begin with, cis-Butadiene was drawn in GaussView, and then optimised using a semi-empirical AM1 type calculation. This type of calculation also gives us the molecular orbitals of the molecule, which are needed to be studied to understand the reaction. The results of the optimisation are shown below.
| Energy (amu) | HOMO | LUMO |
|---|---|---|
 |
 |
The HOMO of cis-Butadiene is antisymmetric with respect to the plane of the molecule, with a nodal plane also occurring here. The HOMO is the π orbitals of the alkene functionalities, with an anti-bonding interaction at the central C-C bond, resulting in another nodal plane. The LUMO is also anti-symmetric with respect to the plane of the molecule with a nodal plane. The LUMO is the π* orbitals of the alkene functionalities (and resulting nodal planes at the centre of these π* orbitals), with a bonding interaction at the central C-C bond.
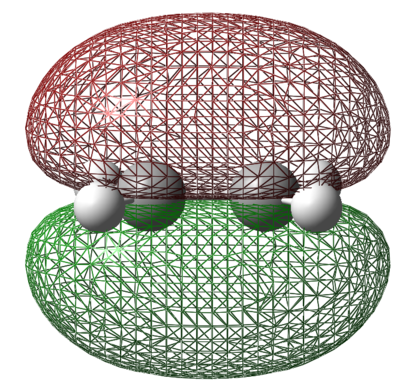
AM1 Optimisation of Ethylene
As the reaction also involves Ethylene, the AM1 optimisation of Ethylene was also run for the sake of completeness. Again, the energy of the molecule from the optimisation is give below, as are both the HOMO and LUMO.
| Energy (amu) | HOMO | LUMO |
|---|---|---|
 |
 |
The HOMO and LUMO of ethylene are what is expected. The HOMO is the π orbital of the alkene functionality which is anti-symmetric with respect to the plane of the molecule. The LUMO of ethylene is the π* orbital of the alkene with a nodal plane through the centre of the bond. The LUMO is also anti-symmetric with respect to the plane of the molecule.
Finding the Transition State of the Reaction:
Now both the reactants have been optimised to the AM1 level of theory, we can go on to look for the transition state of the reaction. To do this, the optimised structures were copied into a new molgroup. Then, they were positioned in the fashion in which we would expect the approach through space of the reactants. The inter-fragment distance was set to approximately 2.0 Å, with the correct alignment of the orbitals involved in the reaction. A optimise to TS (Berry) calculation was set up, with the force constants calculated once, the keyword "opt=NoEigen" was added, and the frequencies were calculated. The level of theory used in the calculation was once again Semi-Empirical AM1. The resulting transition state is shown below, with its energy, and a schematic of the vibration with negative frequency corresponding to the Diels Alder Reaction.
| Transition State | Energy (amu) | Vibration of Reaction | Wavenumber of Vibration (cm-1) |
|---|---|---|---|
 |
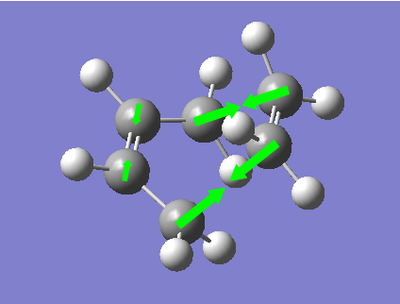 |
The transition state of the reaction is as expected. We observe the ethylene fragment being found above the terminal ends of the double bonds of the cis-Butadiene. In the vibration corresponding to the reaction, we observe the approach of the ethylene molecule towards the end of the double bonds, and the simultaneous bending back of the hydrogens on the ethylene. The ethylene approaches with a synchronous fashion (opposite to the motion of the lowest energy positive vibration where motion is asynchronous) implying that the reaction occurs via a concerted mechanism. We also see an elongation of the double bonds in all the cases indicating the breaking of the bonds into single bonds. We also observe a shortening of the central bond of the cis-Butadiene fragment indicating the formation of a C=C bond.
The bond length of the σC-C bonds being formed in the reaction is given as 2.12 Å. In the transition state, the bonds that were the C=C bonds in the cis-Butadiene reagent have a bond length of 1.38 Å, and the bond length of the bond that will become the C=C in the product has a length of 1.40 Å. This tells us that in the transition states, all of the C-C bonds in the cis-Butadiene fragment have roughly the same bond order as each other. As the bond lengths of the σC-C bonds being formed in the reaction are much longer than typical C-C bonds, we can say that the motion of the molecules from reactants to transition state is mostly down to the changing of the electronic structure of the cis-Butadiene than the formation of the new σC-C bonds.
Now, as we have found the transition state, we can look at its HOMO and LUMO to observe and try and decipher which combination of orbitals from the two reactants result in the Diels Alder Reaction. Below is the results from the calculation of the HOMO and LUMO of the transition state.
| HOMO | LUMO |
|---|---|
 |
 |
From the diagrams of the HOMO and LUMO of the transition state, we can observe which orbitals are involved in the cycloaddition reaction. The HOMO of the transition state shows an interaction between the LUMO of ethylene (π* orbital of C=C) and the HOMO of cis-Butadiene (π orbitals on both alkene functionalities). This tells us that the cycloaddition Diels Alder reaction occurs via the attack of the empty π* orbital of ethylene by the electron rich π orbitals of butadiene. The reaction occurs as we observe a significant spatial overlap of the orbitals in the fragments. This explains why Diels Alder Chemistry is promoted by electron poor dienes and electron rich dienophiles.
Diels Alder Reaction of 1,3-Cyclohexadiene and Maleic Anhydride:
Now we have finished looking at the simple case of the Diels Alder Reaction, we shall consider a more complicated example. Although the molecules are more complicated in this case, the same procedure was used as above to optimise the structure, find the energy of the molecules involved, and generate the molecular orbitals.
AM1 Optimisation of 1,3-Cyclohexadiene:
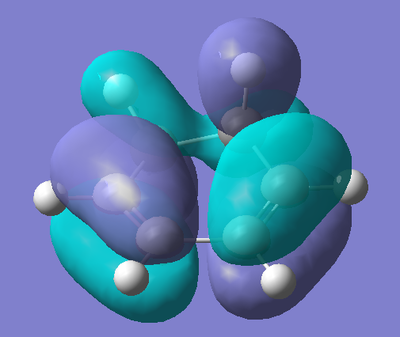
To begin with, 1,3-Cyclohexadiene was drawn in GaussView, and then optimised using a semi-empirical AM1 type calculation. This type of calculation also gives us the molecular orbitals of the molecule, which are needed to be studied to understand the reaction. The results of the optimisation are shown below.
| Energy (amu) | HOMO | LUMO |
|---|---|---|
 |
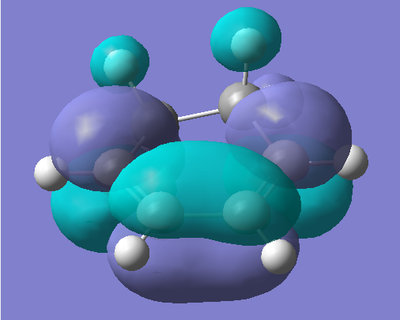 |
The HOMO of 1,3-Cyclohexadiene involves the π orbitals of the alkene functionalities of the molecule with a nodal plane at the central C-C bond (due to the anti-bonding interaction). As the molecule is not planar, we do not observe symmetric molecular orbitals, hence the non-symmetric orbitals on the back two carbons. The LUMO of the fragment shows the π* orbitals of the alkene functionalities, with a bonding interaction at the C-C bond between the two.
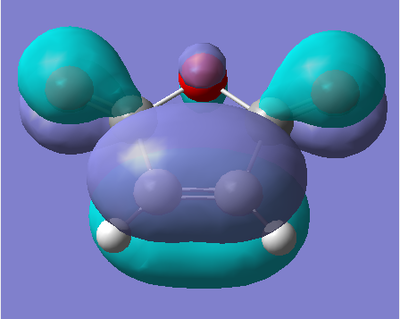
AM1 Optimisation of Maleic Anhydride:
As the reaction also involves Maleic Anhydride, the AM1 optimisation of Ethylene was also run. Again, the energy of the molecule from the optimisation is give below, as are both the HOMO and LUMO.
| Energy (amu) | HOMO | LUMO |
|---|---|---|
 |
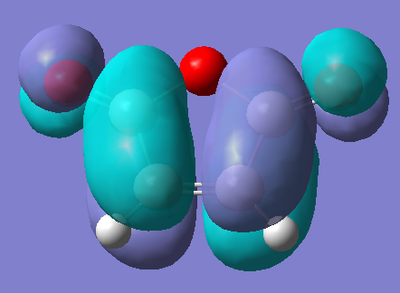 |
The HOMO of maleic anhydride shows the π bond of the alkene functionality in the molecule. We also see the π bond of the carbonyl groups, with an anti-bonding interaction between the alkene π and carbonyl π orbitals. We also see some contribution to the molecular orbital from one of the lone pairs on the oxygen in the ring of the molecule. The LUMO of the molecule shows the interaction between the π* orbitals on the carbonyl and alkene functionalities resulting in a bonding interaction between them. There is no contribution from the oxygen in this case.
Finding the Exo- Transition State of the Reaction:
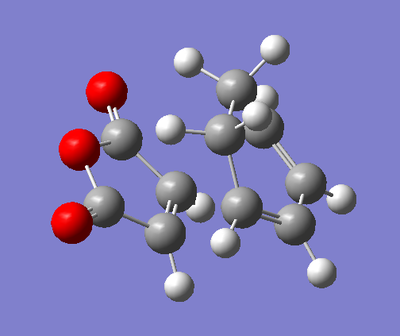
As we are considering a more complex Diels Alder Reaction, the possibilty of Exo- and Endo- products arises. Accordingly, we must consider the transition states of both products. The optimised forms of 1,3-Cyclohexadiene and Maleic Anhydride were copied into the same molgroup and aligned relative to each other in the fashion we would expect of the approach in the reaction. The inter-fragment distance was set to approximately 2.0 Å and the calculation was set up. An opt+freq calculation was run, with optimisation set to TS (Berry) with the force constants calculated once. The AM1 level of theory was used again, and the keywords "opt=NoEigen" were added to prevent the calculation from crashing upon the finding of negative frequencies. The transition state for the exo product is shown below, with its energy, the vibration of the reaction, and the wavenumber of that vibration.
| Transition State | Energy (amu) | Vibration of Reaction | Wavenumber of Vibration (cm-1) |
|---|---|---|---|
 |
 |
In the vibration of the reaction, we observe many processing occurring at the same time. Primarily, the ends of the diene and dienophile approach each other in a synchronous manner implying a concerted reaction. We see a lengthening of the double bonds in both of the molecules which indicates a breaking of their π bonds. A shortening of the σC-C bond in the centre of the diene is also observed which indicates that the formation of a π bond in that position. The ends of the diene and the dienophile are 2.17 Å apart, which indicates even in the transition state, we are a long way from the formation of these bonds.
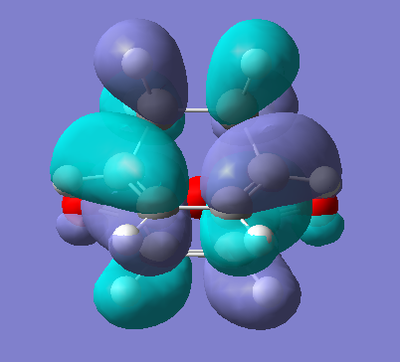
Now, as we have found the exo transition state, we can look at its HOMO and LUMO to observe and try and decipher which combination of orbitals from the two reactants result in the Diels Alder Reaction. Below is the results from the calculation of the HOMO and LUMO of the exo transition state.
| HOMO | LUMO |
|---|---|
 |
 |
Interestingly, the HOMO and LUMO of the transition state of the Diels Alder reaction between 1,3-Cyclohexadiene and maleic anhydride show the overlap of the same orbitals, but in different ways, the overlap between the occupied π orbitals of the diene and the unoccupied π* orbital of the dienophile. The difference arises in how these interactions occur. The HOMO is formed via the constructive addition of these orbitals to each other, whereas the LUMO shows the destructive addition of these orbitals. In the case of the HOMO, we observe a full bonding interaction between the diene and the dienophile, however, in the case of the LUMO, we observe an anti-bonding one, and therefore a nodal plane between the two fragments.
Finding the Endo- Transition State of the Reaction:
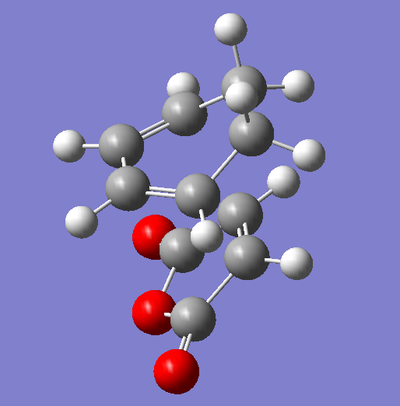
As we have found the exo- transition state, we need to now go on to find the endo- one. The optimised forms of 1,3-Cyclohexadiene and Maleic Anhydride were copied into the same molgroup and aligned relative to each other in the fashion we would expect of the approach in the reaction. The inter-fragment distance was set to approximately 2.0 Å and the calculation was set up. An opt+freq calculation was run, with optimisation set to TS (Berry) with the force constants calculated once. The AM1 level of theory was used again, and the keywords "opt=NoEigen" were added to prevent the calculation from crashing upon the finding of negative frequencies. The transition state for the exo product is shown below, with its energy, the vibration of the reaction, and the wavenumber of that vibration.
| Transition State | Energy (amu) | Vibration of Reaction | Wavenumber of Vibration (cm-1) |
|---|---|---|---|
 |
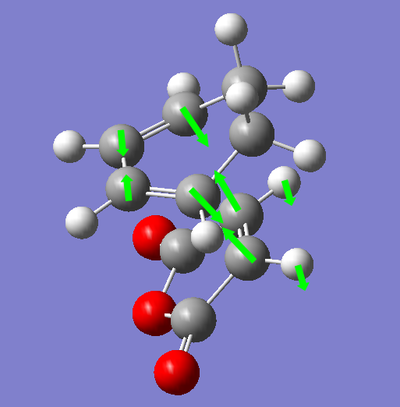 |
In the vibration from the transition state to the product, we observe numerous effects. We see the synchronous approach of the diene and dienophile together implying a concerted reaction to the product molecule. We see a lengthening of the C=C bonds in the diene, implying that the π bond is being broken. We also see a shortening of the central C-C bond between the two alkene functionalities implying that we are seeing the formation of the π bond. The ends of the diene and dienophile are 2.16 Å apart, much longer than a σ bond, therefore, we can propose that the motion from the reaction to the transition state is the electronic reorganisation of the molecules as opposed to the formation of the bond between the two species.
Now, as we have found the endo transition state, we can look at its HOMO and LUMO to observe and try and decipher which combination of orbitals from the two reactants result in the Diels Alder Reaction. Below is the results from the calculation of the HOMO and LUMO of the endo transition state.
| HOMO | LUMO |
|---|---|
 |
 |
Again, in the case of the endo- transition state, we observe the HOMO and LUMO being combinations of the same orbitals, but with different phases. Both molecular orbitals show the overlap between the HOMO of the 1,3-Cyclohexadiene and the LUMO of Maleic Anhydride. In the case of the HOMO, we observe a stabilising effect caused by the constructive addition of these orbitals, and in the LUMO, we observe a destabilising effect due to the destructive addition of these orbitals resulting in a nodal plane between the fragments.
Comparing the Exo- and Endo- Products of the Reaction:
Now we have computed the transition states of the endo and exo products, we can look at the actual product molecules of the Diels Alder reaction between 1,3-Cyclohexadiene and Maleic Anhydride. The 3D structures of these two products are given below.
| Parameter | Exo- Product | Endo- Product |
|---|---|---|
 |
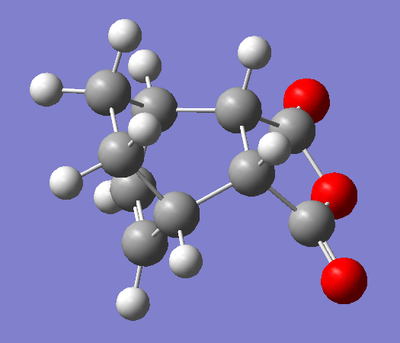 | |
Using the energies of the reactants, the transition states, and the products, we can build up an idea of the stability of the two products from the studied Diels-Alder Reaction, and decide which product is the thermodynamic, and which is the kinetic product. The energies of these species, and the values of ΔEǂ and ΔEreact.
| Parameter | Exo- | Endo- |
|---|---|---|
As we can see, there is very little energy difference between the endo and exo product. Although the endo product is slightly lower in energy than the exo one, the difference of just 1 kJmol-1 is not large enough to say that under thermodynamic conditions the endo product would predominate, we would most probably get mixtures of the two products. The transition state for the endo product is more stable than that of the exo product by 3 kJmol-1, which is probably a large enough difference to observe a significant effect if the reaction was done under kinetic conditions. Therefore, we can say that the endo product is the the kinetic product.
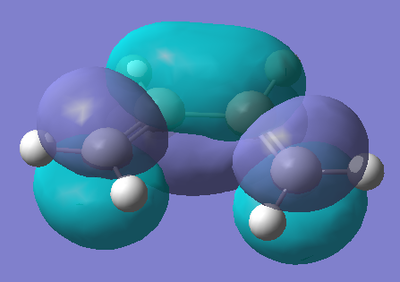
One would initially think that the endo product (and transition state) would be less stable than the exo due to the increased steric bulk around the molecule. However, this is more than compensated for by the presence of a secondary orbital overlap that is present in the transition state for the endo product, but not in the exo one. In order to see this secondary overlap, we need to decrease the isovalue of the Molecular Orbitals to 0.05.
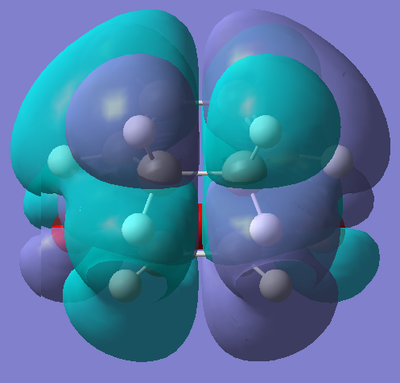 |
 |
|---|
The first picture shows a secondary overlap between one end of the π* orbital of the alkene functionality in the maleic anhydride fragment and the orbitals around the saturated part of the diene. We also see a secondary interaction between the π* orbitals of the carbonyl groups in the maleic anhydride and the π clouds on the alkene functionalities in the diene. It is a combination of these two stabilising secondary effects that give the endo transition state added stability, so much so, it is lower in energy than the exo transition state. Both these effects occur in the HOMO. It has been said in literature that the secondary orbital overlap occurs between the HOMO of the diene and the LUMO of the dienophile [5]. In the case of the exo transition state, we would also expect to observe steric clashes between the carbonyl groups and the oxygen in the ring with the hydrogens bond to the two sp3 carbons in the 1,3-cyclohexadiene ring. This will disfavour the approach of the two fragments and increase the energy of the transition state.
Improving the Calculations:
There are two main areas in which this investigation can be improved, computational aspects, and practical aspects. We could use more accurate calculation types with better basis sets that account for electron correlation effects and include more orbitals amongst others. This would result in the calculated values being more accurate and therefore a better representation of what is actually occurring. We also need to take into account physical aspects of the reaction system, such as steric and substituent effects. By varying the substituents on the species investigated, we could gain a greater understanding of the reaction. We could also go on to investigate solvent effects on the system, and how solvents of different polarity or whether or not they can donate or accept H-bonds can stabilise (or destabilise) the reactants, transition states and products with respect to each other. By accounting for these, we will be able to understand these reactions to a much greater depth.
Links to Calculation Output Files:
| Calculation | Reference |
|---|---|
| AM1 Optimisation of Butadiene | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:CIS_BUTADIENE_AM1_OPTIMISATION.LOG |
| AM1 Optimisation of Ethylene | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:ETHYLENE_AM1_OPTIMISATION.LOG |
| Butadiene + Ethylene TS Optimisation | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:FINDING_TS_OF_CYCLOADDITION_ATTEMPT_1.LOG |
| Butadiene + Ethylene TS Frequency Calculation | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:FINDING_TS_OF_CYCLOADDITION_ATTEMPT_1_FREQ_ANAL.LOG |
| AM1 Optimisation of 1,3-Cyclohexadiene | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:CYCLOHEXADIENE_OPTIMISATION.LOG |
| AM1 Optimisation of Maleic Anhydride | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:MALEIC_ANYHDRIDE_OPTIMISATION.LOG |
| Exo Product Optimisation | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:EXO_PRODUCT_OPTIMISATION.LOG |
| Endo Product Optimisation | https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:ENDO_PRODUCT_OPTIMISATION.LOG |
References:
- ↑ A.Cope et al, J. Am. Chem. Soc., 1940, 62, pp 441-444 DOI:10.1021/ja01859a055
- ↑ O.Diels, K.Alder, Justus Liebig's Annalen der Chemie, 1928, 460 (1), pp 98-122:DOI:10.1002/jlac.19284600106
- ↑ O.Kikuchi, Tetrahedron Letters, 1971, 27, pp 2791-2800:DOI:10.1016/S0040-4020(01)98070-6
- ↑ D.Craig, J.J.Shipman, R.B.Fowler, J. Am. Chem. Soc, 1961, 83 (13), pp 2885-2891:DOI:10.1021/ja01474a023
- ↑ B.Pandey, P.V.Dalvi, Angew. Chem. Int. Ed. Engl, 1993, 32 (11), pp 1612-1613:DOI:10.1002/anie.199316121