Rep:Mod:rvirdee1
3rd Year Computational Lab Module 1: Structure and Spectroscopy
Rajvinder Virdee
Introduction:
In recent times, Computational Chemistry has advanced to such a degree, not only can we use it as a purely theoretical technique, but we can also use to to predict the outcome of chemical reaction to a high degree of accuracy. With the development of computational methods, we can investigate the relative stability of products of a reaction via a purely energetic approach, we can also mathematically predict the molecular orbitals and various spectra (including IR and NMR) to be used as a supplimentary technique to conventional prediction of the outcome of reactions.
We have used various methods in this investigation to study numerous reactions. A molecular mechanics based calculation (MM2[1]) treats molecules in a classical fashion, as simple masses on springs. This allows us to make a simple approximation of the energy by minimizing various energies of the system by treating each individual bond as a spring. By summing this across the whole molecule, we can calculate the derivative of the total energy with respect to a small change in atomic coordinates, and by minimizing this to a set threshold, we arrive at a minimum energy. PM6 is an advance on this technique, and is classified as a semi-quantum technique. The calculation is still effectively based on the idea of masses on a spring, however, it also has some contribution from quantum mechanics in the form of electronic distributions in a molecule, and to a certain limit can discriminate between electron donating and withdrawing groups and their effect on molecular structure. The final model investigated is DFT modelling[2]. This a full quantum mechanical model concerning the spatial dependency of electronic distribution. As it is a full quantum method, it gives the best optimization of the structure.
Various Chemical systems were modelled in the lab, including dimerisations of dienes, nucleophilic addition to pyridinium rings, secondary orbital overlaps, stereochemistries, and ending with the mini-project based on DFT calculations.
The Hydrogenation of Cyclopentadiene dimer:
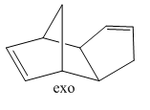
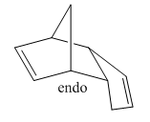
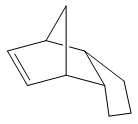
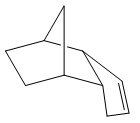
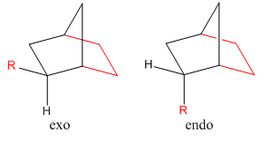
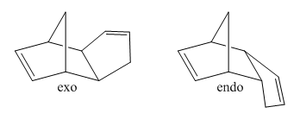
Cyclopentadiene will readily undergo a Diels-Alder [4+2] cycloaddition with another equivalent of itself to form a single dimer. We know that Diels-Alder reactions of such molecules can result in two possible products, namely, exo and endo. These prefixes are used to describe the relative stereochemistry of the added substituent to the longest bridge in the molecule. The "endo-" isomer is the form of the molecule where the substituent is "syn-" with respect to the longest bridge, whereas the "exo-" isomer is the form where the substituent is "anti-" with respect to the longest bridge. Once this has occured, we have 2 different alkene functionalities present in the molecule. The ability for this bond to be hydrogenated will be investigated, and which one is more favourably hydrogenated will also be examined.
Dimerisation of Cyclopentadiene:
 |
 |
|---|
  |
|---|
The Exo and Endo isomers are shown to the left. The bridge highlighted in red is the longest bridge, and the bridge the stereochemistry of the molecule is determined with. Once this has been applied to a bicyclic system such as the dimer of cyclopentadiene, we can asign the two isomers as seen to the left.
The results from the MM2 calculation for the Exo- and Endo- product are given to the left.
All of the energies were calculated by the software package in kcalmol-1, and there then appropriately converted into the standard unit of kJmol-1. The values of each contribution to the total energy have been quoted to the same degree of accuracy as the output from the MM2 force field minimizations, however, the inaccuracies in these have been accounted for by quoting the total energy of each isomer to a single decimal place. We know there is an inherent lack of accuracy in force field methods, and hence, these errors have been compensated for in this way.
As we can see from the calculated data from the minimizations, the exo- product has a lower energy than the endo-, thus indicating that it is the exo-dimer that is the thermodynamically more stable. So, under equilibriating conditions, and the reaction being placed under thermodynamic control, we would expect the exo-dimer to be the predominant product. However, the Diels Alder dimerisation of cyclopentadiene is a reaction that does not occur under equilibriating conditions. Although theoretically, [4+2] cycloaddition reactions are reversible, in practice, they very rarely are. In this case, as the reaction is not reversible, it is said to be under kinetic control.
As we have now deduced that the dimerisation reaction of cyclopetadiene is under kinetic control, we must study the transition states of the two isomers, exo- and endo-, to determine which is the predominant product. We know from the selection rules of [4+2] cycloaddition reactions that the two hydrogen atoms found at the edge where the two cycles meet must be cis to eachother, however, that still does not differentiate between the two possible products. However, as were are using two cyclic (cylcopentadiene) symmetric (C2 symmetry) equivalents of the same compound, one acting as the diene, one as the dienophile, we can look to what is know as "The Endo Rule"[3] for our solution.
| exo product | endo product |
|---|---|
 |
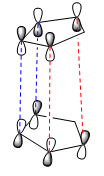 |
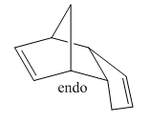
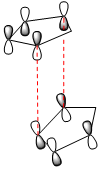
The "Endo Rule" tells us that the endo-product of a [4+2] cycloaddition reaction has the lowest energy transition state, and is thus the kinetic product. Once this idea is extended to the case of cyclic symmetric compounds, we can say that the endo-product is always the predominant product of the reaction. This can be understood by considering the orbital overlap occuring when the diene and dienophile approach in space. We already know that these reactions occur via electron donation from the ends of the π system of the diene into one of the π* bonds of the dienophile, thus making the reaction a HOMO-LUMO based reaction.
The differnce in the orientation of the product is due to the direction in which the dienophile approaches the diene. In the case of the exo-product, the two molecules approach almost edge to edge with overlap between the orbitals at the extremities of the molecules. However, in the case of the endo-product, the two molecules approach one on top of the other. The dashed lines drawn in red in each of the diagrams indicate the interaction between the orbitals that results in the actual reaction, i.e. the formation of the two σ bonds. In each of the two approaches, we observe similar overlap between the two sets of orbitals forming the sigma bond. However, in the case of the endo product, we observe a second favourable overlap, that between the central two lobes of the π system on the diene and the non-reacting π* orbital in the dienophile, demonstrated by the blue dashed lines. The presence of this second favourable interaction between the molecules orbitals creates a stablising effect not present in the exo-approach, and thus lowers the energy of the transition state of the endo-product[4]. This makes this transition state lower in energy that the transition state for the exo-product, and hence why the endo-product is the kinetic product of the Diels Alder reaction resulting in the dimerisation of cyclopentadiene.
Hydrogenation of the Dimer:
 |
|---|
|
|
|---|
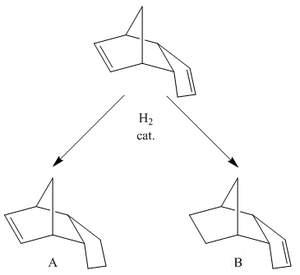
As we have now decided that the dimerisation of cyclopentadiene results in the formation of the endo-product, we can go on to look at the hydrogenation of that coumpound. In the cyclopentadiene dimer, there are two carbon-carbon double bonds, so, what happens if just one equivalent of hyrdogen (H2) is used? Which of the double bonds is preferentially hydrogenated? The mechanism for hyrogenation and the orbitals involved in each will be almost identical, so similar in fact we can consider the two transition states to have the same energy, and thus ignore which product is kinetically more favourable. This can be done as to all intents and purposes, the two double bonds are at the edges of the compound, so in very similar chemical environments, therefore, we can assume there is no steric interaction favouring (or disfavouring) the approach of the reagents causing hydrogenations, and in more general terms, the rate of hyrdogenation of both double bonds is the same. Therefore, this becomes a purely thermodynamic problem.
In light of this, we must now look at the energetic stabilities of each of the hydrogenated products, just as we investigated which dimer was formed. An MM2 force field calculation was set up for each of the two molecules, set to minimize their respective energies (whilst ensuring the product remains in the endo-form). The calculation splits the results into 8 sections, concerning the different energies of the molecule: Stretch; Bend; Stretch-bend; Torsion; Non-1,4 Van der Waals interactions; 1,4 Van der Waals interactions; Dipole-Dipole interactions, and the total energy of the molecule. By analysing this data, we can rationalise which of the two double bonds is preferentially hydrogenated and hopefully, explain why. The results of the calculations are shown in the table to the right. As we can see from the data generated as the output of the calculation, hydrogentation of the carbon-carbon double bond in the 6-membered ring is energetically more favourable than hydrogenation of the bond in the 5-membered one. The energy difference between the two products is quite considerable, 20kJmol-1, the majority of which, as we can see from the data, seems to originate from just two of the determined parameters, Bending, and 1,4 Van der Waals interactions.
|
|
Firstly, we shall consider the difference in the bending energies of the two molecules. Wherever a double bond is positioned in a molecule, it creates an area of rigidity due to restricted rotation, stretching and bending, due to loss of the favourable p-p orbital overlaps. However, where in a molecule the bond is found effects the degree to which this restriction effects these characteristics of the whole molecule. In the cyclopentadiene dimer, the six membered ring and bridge will tend to influence the total energy of vibrations, stretches and bends in the molecule more than the five membered one. Therefore, necessarily, when the double-bond is found in the six membered ring, we observe restricted movement in that area of the molecule, effectively acting like a conformational lock, forcing the molecule into rigidity, hence the high energy of bending. On the other hand, the double bond being positioned in the five membered ring only imparts a small effect on the bending of the molecule, as any restriction is reduced by the σ bonds between it and the ring. Hence, the product in which the double bond is not in the six membered ring, product B, has the lowest, and therefore more stable, contribution to the total energy by bending. To understand why product A has and overal higher contribution to the total energy from 1,4 Van der Waals interactions, we need to consider the three dimensional structure of the molecules. If we look at the three dimensional animations of the products, we can look for the 1,4 Van der Waals interactions that are unfavourable. Once this is done, we can see there are more of these unfavourable interactions for product A, and hence the more unfavourable contribution to the overall energy. We observe very little difference in the numerical answers for the other calculated parameters, the discrepancy between the relative energies of the two molecules is due to bending and 1,4 Van der Waals. Therefore, we can say that product B is the more stable product. So, going back to the posed question, if one equivalent of H2 was added to the endo-dimer of cyclopentadiene (in the presence of the correct catalyst), and the reaction was done under thermodynamic conditions, the product would be product B.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring:
We can extend these techniques we have learnt from the hydrogenation problem above to more complex reaction methods, for example the attack of a nucleophile on an electron deficient system. In this case, we shall investigate the relative stereochemistry of two different pyridinium reagents to see if this approach can help us to decide where, and by which face the nucleophile will approach and attack.
Nucleophilic Attack by Grignard Reagent:
In the first case, we will investigate the attack of a carbon-based nucleophile in the form of a Grignard Reagent on an optically active prolinol derivative. By analysing the electronic distribution throughout the molecule, we can deduce that there is one site that is the most probable site of attack. The reaction can be sumarised in the scheme below. The optically active chiral centre is shown by the carbon labelled with a *.
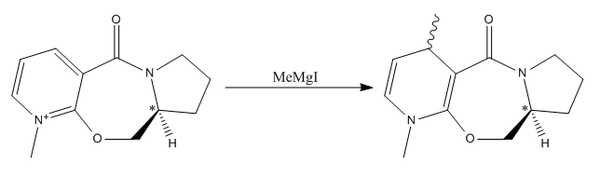
By generating 3D models of the starting material in ChemBio3D, we can see not only is there various stereochemistries around the chiral centre, but we also need to consider the stereochemistry of the carbonyl group with respect to the pyridinium ring. We observe two separate cases for the stereochemistry of that group, it can either be found above the plane of the ring, or below it. These two forms have distinctly different energies, found by using MM2 energy minimizations, and can thus be considered as conformers. The results of these calculations are extremely important to aid the understanding of the orientation of addition of the methyl group and the resulting stereochemistry of the molecule.
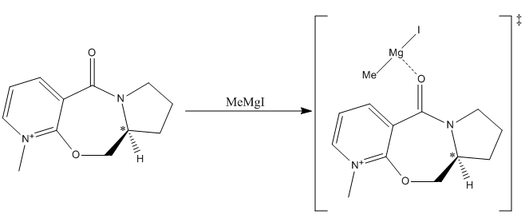

The energy difference of the molecule between the two orientations of the carbonyl group with respect to the pyridinium ring is 6.1kJmol-1, enough to classify the two as conformers. As the conformer with the carbonyl above the plane of the molecule is of lower energy, we can say that it is the most stable conformation of the molecule, and the form that is most present in a sample. This has a major effect on the outcome of the reaction. The attack of a magnesium based grignard reagent on this type of species initially involves an interaction between the magnesium and the carbonyl oxygen[5]. This interaction forces the carbon based nucleophile to attack from the same face as the carbonyl is found with respect to the ring. As we have shown via the MM2 Force Field calculations that the starting product is more stable when the carbonyl is above the plane of the pyridinium ring, therefore, due to the interaction between the carbonyl oxygen and the magnesium in the grignard reagent, the favoured product of the reaction is that with the methyl group also above the plane of the carbonyl. We can demonstrate that the stereochemical control of the reaction is due to this magnesium-oxygen interaction by running MM2 calculations of two forms of the product, one with the methyl group above the plane, one below. The energies of the two forms of the product are almost identical, therefore the preference of products cannot be due to thermodynamics.
Nucleophilic Attack by Aniline:
We can extend this approach to more complicated reagents with other nucleophilic species. We will now investigate the attack of an aniline molecule resulting in transfer of -NHPh as the nucleophilic species. Just as before, we have used the MM2 Force Field to minimize the energies of two forms of the reagent, one with the carbonyl group above the plane of the aromatic system, and the other where the carbonyl is below the plane. However, unlike the previous case, there is a negligible difference in energy between the two forms, which indicate the two conformations are just as likely and therefore both exist in the reaction mixture.

As we can see from these calculated energies, 0.1kJmol-1 is not sufficient for one conformer to be present in a dominant proportion. Therefore, the stereochemical outcome of attack of this molecule by a nucleophile, in this case aniline, must be determined by the energy of the product molecule, not the reagents. Unlike in the case of the Grignard reaction where we could get complexation of the magnesium to the carbonyl oxygen, this time, such interaction cannot occur. Therefore, the product will most probably be determined by the sterics of attack by the aniline, so we would expect the least hindered face of the molecule to be attacked[6].
There is an extremely large energy difference between the two stereoisomers of the substituted product, approximately 100kJmol-1, an extraordinarily large amount. This would imply that the reaction between the pyridinium ion and aniline would only give one product, that where the added phenyl substituted amine is above the plane of the ring system. This stereoisomer of the product would represent almost 100% of the the total product of the reaction when performed under thermodynamic conditions. To further investigate this problem however, we could need to consider 2 other factors that could push the reaction to either stereoisomer:
- Energy of Transition State: The energy of the transition state should be analysed to observe whether or not the thermodynamic product is also the kinetc product. We could have such a case where the kinetic and thermodynamic products of the reaction are different, hence, this is an area that should be further investigated to say which product would dominate under given conditions.
- The Solvent: Different solvents can stabilise similar to differing degrees. We could get the case where one solvent lowers the energy of the second product, and raises that of the first by such significant amounts, the resulting dominant product could infact reverse. This however would be extremely difficult to predict or calculate, and would probably only be resolved via a practical means. We could also be under the conditions where the solvent is in fact aniline, and we would then need to investigate how aniline would interact with each molecule, but again, this would require a more complicated set of calculations than those explored so far.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol:
In the total synthesis of Taxol proposed by Paquette, we observe an intermediate with a carbonyl group that can be formed with two different stereochemistries, the carbonyl pointing up or down. In this molecule, we observe atropisomerism, hence, the two isomers cannot be interconverted in situ. Therefore, it is of upmost importance to synthesize the molecule with the correct stereochemistry of the carbonyl group, as its stereochemistry will dictate any further reactions occuring at that centre. Therefore, it is important to investigate which of the stereochemistries is the most stable and thus the predominant product. Then, further synthesis can be designed to give the final target molecule. In this intermediate, we also observe extremely slow functionalisation of the alkene moiety in the molecule, which is due to the effect known as "Hyperstable Alkenes", which shall also be investigated.

Determining Stereochemistry of the Carbonyl Group:
As discussed above, it is of upmost importance to know the relative stereochemistry of the carbonyl group in the molecule. Any further reaction that is required to be done at that carbonyl to progres the reaction towards the final target molecule (Taxol) will have to be designed to take into account this stereochemistry. The differing stereochemistry of this centre can have a profound effect on the structure of the final product. This importance is accentuated as the target molecule is to be used for medicinal purposes, more specifically, as an anti-carcinogenic drug. To determine which stereochemistry is the most stable, and thus the product most likely to be found in solution, an MM2 Force Field calculation was set up for each of the isomers, set to minimize their energies. Then, we can compare the results, determine which is the most stable, and then design the rest of the synthesis appropriately.
As we can see from the calculations, the more stable stereoisomer of the intermediate is that when the carbonyl group is orientated below the plane of the ring systems. The energy difference of ca. 40kJmol-1 is more than enough to make this isomer to be the dominant product assuming the step forming that product is done under thermodynamic control. Again, to determine whether or not this is truly the case, the synthesis to form the carbonyl group, both reagents and conditions, is required to decide whether or not it is made under thermodynamic or kinetic control, and therefore, we would be able to perform the appropriate calculations to determine which stereoisomer would be the dominant product.
Extraordinary Reactivity of the Alkene Functional Group:
It has been experimentally observed that the reactivity of the alkene moiety in the intermediate of the synthesis is not what is to be expected. One would usually expect reactions such as electrophilic attack, addition, and general functionalisation to be facile in such as system, however, we observe extroaridinarily slow rate of reactions. This can be explained by the phenomenon known as "Hyperstable Alkenes"[7]. An alkene is defined as hyperstable if they have a "negative olefin strain" (negative OS). To calculate the OS, we must compare the values of strain (in our case, torsion) of the alkene, and its hydrogenated equivalent. If the torsion of the hydrogenated product is greater than that of the alkene, then we can call the molecule a Hyperstable Alkene. To do this, MM2 Force Field energy minimizations were performed to calculate the respective energies of the alkene and the hydrogenated product.
Carbonyl Above Ring System:
The results of the MM2 energy minimizations for the intermediate and its hydrogenated product are given below.
As we have defined above, the definition of a hyperstable alkene is that where the hydrogenated product has a higher degree of torsional strain than the alkene, so, in the case of the intermediate where the carbonyl is above the ring...
OS = Torsion(alkene) - Torsion(hydrogenated) = 91.6026 - 101.2337 = -9.6311kJmol-1
Therefore, we can call the case where the carbonyl is above the plane a Hyperstable Alkene.
Carbonyl Below Ring System:
We shall also consider the case of the Carbonyl being below the plane. The results of the MM2 energy minimizations are given below.
As we have defined above, the definition of a hyperstable alkene is that where the hydrogenated product has a higher degree of torsional strain than the alkene, so, in the case of the intermediate where the carbonyl is below the ring...
OS = Torsion(alkene) - Torsion(hydrogenated) = 95.8382 - 105.1253 = -9.2871kJmol-1
Therefore, we can call the case where the carbonyl is below the plane a Hyperstable Alkene.
Bredt's Rule:
Bredt's Rule [8] tells us that for small rings, it is unfavourable to have bridgeheaded alkene functionalities. This is due to excessive strain in the molecule caused by the sp2 hybrid orbitals on the carbon atoms wanting to remain as close to 120o as possible, but being forced away from ideality by the geometry of the complex. If we did have a bridgeheaded alkene functionality, we would be forcing a trans double bond in the cyclic system, which would be too unfavourable due to ring strain and torsional strain. In our case, however, the rings we are dealing with are much better, and the molecule can orientate itself sufficiently to allow a stable geometry of the double bond at an angle as close as possible to 120o.
We can extend the theory of Bredt's Rule to the case of the attack of an electrophile at the electron rich double bond. Due to the steric bulk around the bridge, we would expect the electrophile to attack the less hindered end. This would result in the formation of a carbocation at the point of the bridge. This carbocation would be extremely unstable due to the geometry of the site. Attack of an electrophile at the less hindered end would form a carbocation with the positive charge being in the form of an empty p orbital on carbon, giving it a hybridisation of sp2. The favoured geometry of an sp2 carbon is trigonal planar with coplanar bond-angles of 120o, with an orthogonal empty p orbital. However, the bridge will try to force the geometry closer to a tetrahedral/pyramidal structure, which would be extremely unstable. This would result in attack by electrophile on the alkene moiety to be unfavourable.
Regioselective Addition of Dichlorocarbene:
In previous calculations done so far in this module, we have only considered a Molecular Mechanics approach to determine reactivity and products of reaction. However, this approach does have its downfall, especially when electronic density has a major role to play in the reaction. This failure of the Molecular Mechanics approach can be clearly seen in the example of the dimerisation of cyclopentadiene. MM2 calculations tell us that the exo product should be the dominant product due to its higher stability. However, it does not take into account for the secondary orbital overlap in the endo approach, so discounts the added stability of this interaction. We can overcome this problem by using an approach that will take into account electronic density of the molecule, which as we know has a profound effect on reactivity.
Secondary Orbital Overlap Effecting Reactivity:
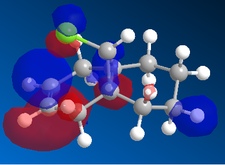
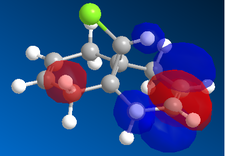
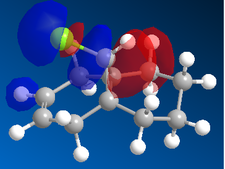
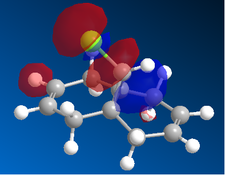
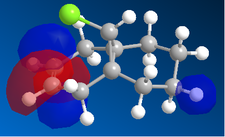
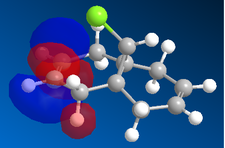
In this section of the module, we will investigate the attack of an electrophile file (e.g. Dichlorocarbene or a peracid) on a specific asymmetric molecule with two alkene functionalities. The Molecular Orbitals of the molecule will be calculated and investigated and using the results, we should be able to predict the site of electrophile attack on the molecule. To fully appreciate this technique, we will make a comparison between the original molecule, and a dihydrogenated version of the molecule with just one alkene group.
| Molecular Orbital | Dialkene | Monoalkene |
|---|---|---|
 |
 | |
 |
 | |
 |
 | |
 |
 | |
 |
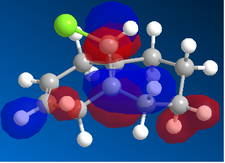 |

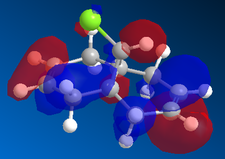
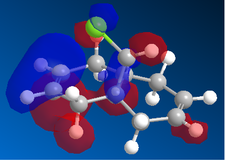
In the orbital defined as HOMO-1 for the dialkene molecule, we can clearly see a secondary orbital overlap between electron density on the chlorine atom, and the π cloud of the double bond endo to it. This overlap coupled with the electronegative characteristic of chlorine would result in electron density being withdrawn out of the π cloud, thus reducing its electron density. This would result in a reduced suseptability towards attack by an electrophile.
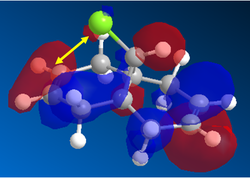
Any attack by an electrophile would occur via attack of the π* orbital of the alkene. In the case of the dialkene, we observe the π* orbital of the alkene exo to the chlorine as the LUMO, therefore, we can expect electrophilic addition to that alkene group to be especially facile. The π* orbital of the alkene endo to the chlorine is the LUMO+2 which is much higher in energy, therefore, attack by an electrophile towards that functional group would be much less favourable.
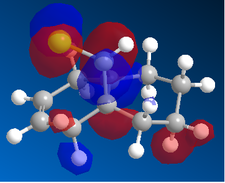
Now, if we consider the case of the monoalkene, we still do see a secondary orbital interaction. However, in this case, the orbitals on the chlorine and the lobe of the π cloud of the alkene are of opposite phases, therefore, this interaction offers no stabilisation of the alkene, in fact, we may observe an destabilisation. Never-the-less, unlike the case of the dialkene, we would not observe any removal of electron density from the the double bond, and therefore, no reduction in suseptability towards attack by an electrophile.
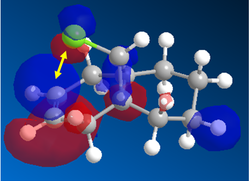
In the case of the monoalkene, the π* orbital of the alkene is in the LUMO+1 orbital (for dialkene, equivalent π* orbital is in LUMO+2), therefore, we can say the equivalent π* orbital for the monoalkene is lower in energy than in the case of the dialkene, and we would therefore expect it to be more suseptable to attack by an electrophile. We can rationalise this as in the case of the monoalkene, we do not observe any secondary orbital overlap to stabilise the carbon-carbon double bond to attack by an electrophile, thus, it is more accessible in energy for the monoalkene than the dialkene.
Calculation of Bond Energies:
Above, we have tried to rationalise the energies of the alkene groups in the molecules by calculating the molecular orbitals, and using the idea of secondary orbital overlaps to see if any stabilisation occurs of either of the groups. We can try and justify these claims by calculating the bond oscillation frequencies using a Gaussian based calculation. To do this, we used the density function approach in Gaussian. Firstly, the molecular structures we optimised using MM2 Force Field, then PM6 MOPAC energy minimizations. Then, the structures were exported to GaussView, and were subjected to B3LYP/6-31G(d,p)Gaussian Geometry Optimization and Frequency Calculation (where B3LYP denotes the approximation used for the orbitals, and 6-31G the basis set used for the calculations.
Dialkene Bond Energies:
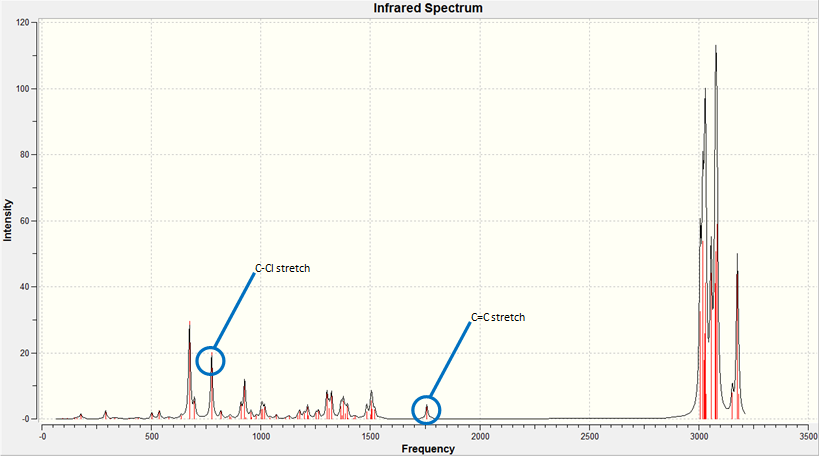
The IR spectrum of the Dialkene molecule was generated using the method described above. Once the vibrations were generated, we used the results to analyse the vibrations of the key functional groups in the molecules, the C-Cl stretch and the two C=C stretches. From the wavenumbers of the vibrations, we can calculate the relative energies of each bond in kJmol-1, a convenient unit to compare across different molecules. The IR spectrum generated and the key vibrations are shown below.
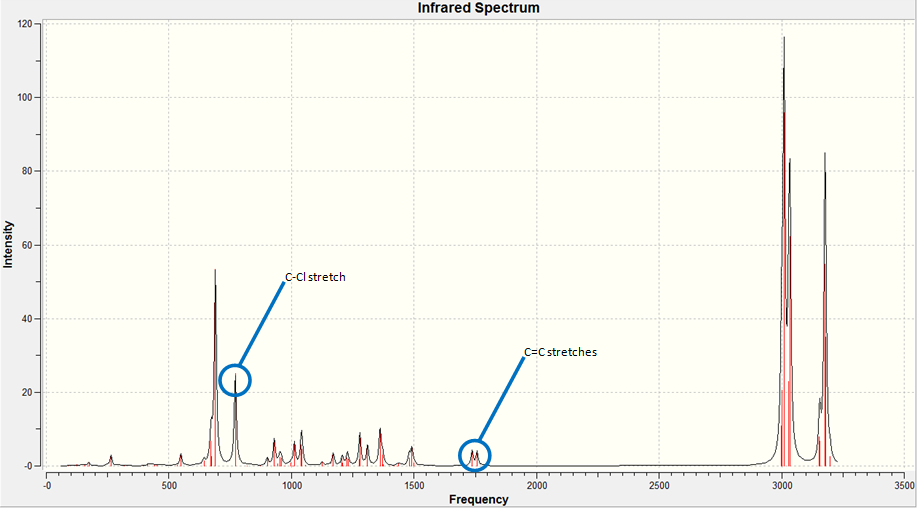
| Vibration | Schematic of Vibration | Energy (cm-1) | Intensity | Energy (kJmol-1) |
|---|---|---|---|---|
 |
||||
 |
||||
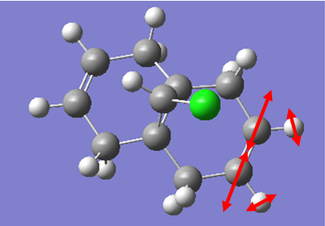 |
As we can see from the energies calculated from the spectra, the endo C=C bond is higher in energy than the exo C=C (by c.a. 1.17%). This indicates that the endo C=C bond is stronger than the exo one, as more energy is required to cause the vibration. This supports the idea that the endo C=C is stabilised by secondary orbital overlap with the chlorine towards attack by an electrophile, whereas the exo C=C does not have any similar stabilisation.
Monoalkene Bond Energies:
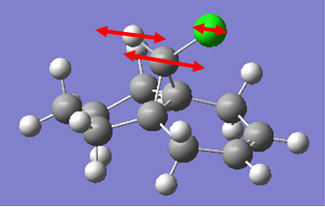
For the monoalkene reagent, the same style of calculation was performed as in the case for the dialkene. The vibrations were calculated generating the IR spectrum, and energies from these in the form of wavenumbers were converted into kJmol-1 to give a better unit to compare between structures.
| Vibration | Schematic of Vibration | Energy (cm-1) | Intensity | Energy (kJmol-1) |
|---|---|---|---|---|
 |
||||
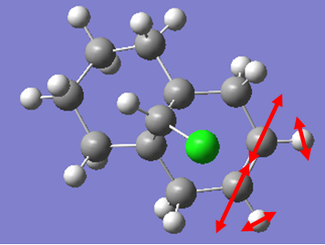 |
In the case of the monoalkene, the energy of the C=C stretch is almost identical to the endo C=C stretch in the dialkene, this was not to be expected, as we would expect the bond to be stronger and more stable in the dialkene than the monoalkene. However, this can be explained by the differing structures of the two molecules. The 6 membered saturated ring bound to the monoalkene has far more flexibility than the unsaturated ring in the case of the dialkene. This would allow the vibration to occur at higher energies, as the more flexible group would tend to act less as a conformational lock damping vibrations.
To fully appreciate the lack of secondary orbital overlap in the case of the monoalkene, we can also compare at the C-Cl stretches. In the case of the monoalkene, the bond is 0.04kJmol-1 stronger than the dialkene. This can be explained by the secondary orbital overlap. In the case of the dialkene, the secondary orbital overlap will allow the chlorine to remove electron density from the π cloud of the alkene group. This would increase the electron density on chlorine and thus polarise the C-Cl bond further. This would result in a destabilisation of the bond thus resulting in the vibration occuring at a lower energy in the case of the dialkene than the monoalkene.
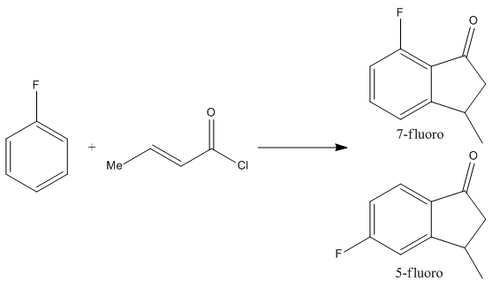
Microwave Assisted One-pot Synthesis of 1-Indanones from Arenes and α,β-unsaturated Acyl Chlorides:
For the DFT based Molecular Orbital method miniproject, I shall be studying the Microwave Assisted One-pot Synthesis of 1-Indanones from Arenes and α,β-unsaturated Acyl Chlorides as performed by W. Yin, Y. Ma, J. Xu and Y. Zhao[9]. In their research, they studied this reaction with numerous reagents, however, the one in particular I shall focus on is the reaction between fluoro-benzene and crotonoyl chloride yielding fluoro-3-methyl-1-Indanones. The reaction forms 2 regioisomers of the prodcut, depending on the oreintation the molecules react in, forming a mixture of the 5-fluoro-3-methyl-1-indanone and the 7-fluoro-3-methyl-1-indanone.
Mechanisms of Formation of Products:
The literature proposes that the reaction occurs in a tandem Friedel-Crafts acylation and a Nazarov Cyclization of the substituted benzene with the α,β-unsaturated acyl chloride in the presence of a Lewis Acid (in the form of AlCl3) and done under microwave irradiation. The synthesis under the conditions I am studying showed very little selectivity of the two isomers with a reported 41:59 ratio 5-fluoro:7-fluoro of the two isomers. This seems to indicate the reaction is almost under no control whatsoever (i.e. very little effect favouring each isomer), implying the reaction is under statistical control making it ideal for this type of study. The proposed origin of the two isomers is due to the two possible sites that the initial Friedel-Crafts acylation could occur, ortho or para on the fluorobenzene.
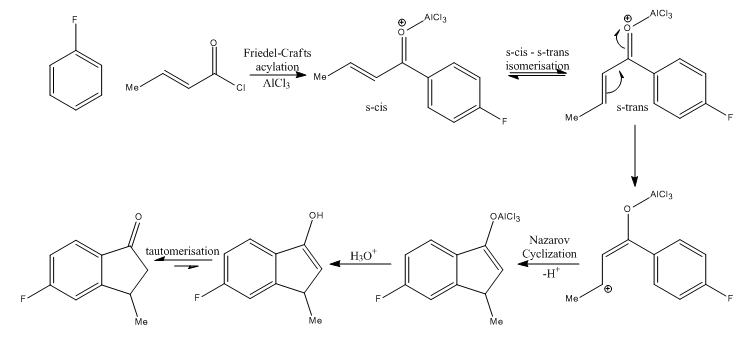
Formation of 5-fluoro-3-methyl-1-indanone:
The proposed reaction mechanism for the formation of the 5-fluoro substituted product is given below. As discussed above, the reaction procedes via an inital Friedel-Crafts acylation with attack the para position with respect to the fluorine, followed by a Nazarov cyclization.
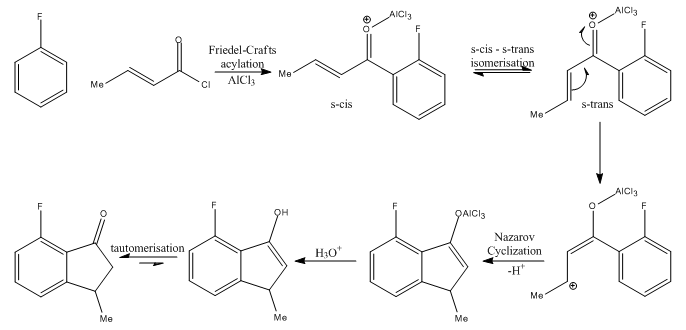
Formation of 7-fluoro-3-methyl-1-indanone:
The proposed reaction mechanism for the formation of the 7-fluoro substituted product is given below. As discussed above, the reaction procedes via an inital Friedel-Crafts acylation with attack at the ortho position with respect to the fluorine, followed by a Nazarov cyclization.
Favouring of 7-fluoro over 5-fluoro product:
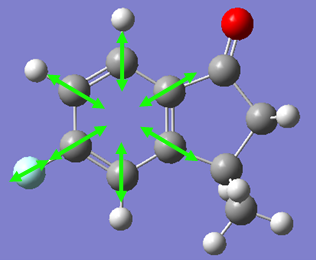
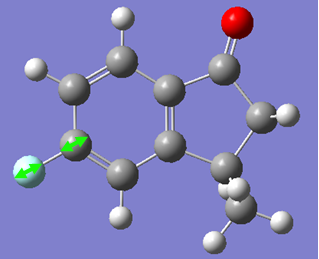
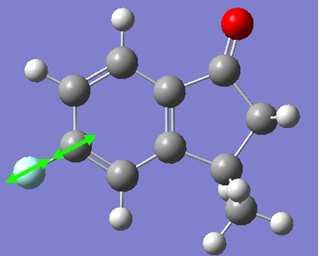
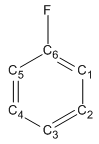
| Carbon | Mulliken Charges | Fluoro-benzene |
|---|---|---|
| ||
To the left, you can see the Mulliken Charges calculated of each of the carbon atoms in the substituted benzene ring. This was done using the MOPAC interface with a PM6 method set to calculate the Mulliken charges. Due to C2 symmetry in the molecule, we can say C1 is equivalent to C5, and C2 is equivalent to C4. From the results from the calculations, we can see that there is a skewed charge distribution on the substituted benzene. C1 and C3 show the highest charge density in the molecule (significantly higher than C2 and C6) therefore we can view these two sites as the most probable sites of attack by the electrophile (acyl cation).
We can see from the data that there is a higher charge density on the C1 position, than the C3 position. It should be noted that attack at C1 corresponds to the 7-fluoro product, and the C3 position the 5-fluoro product. The ration of the Mulliken charges between the C1 and C3 postions is approximately equal to the ratio of the product distribution recorded (1.235 for the Mulliken charges and 1.440 for the product distributions) however, there is a reasonable difference which would seem to imply that the difference in the charge densities is not the only controlling factor in deciding the relative proportion of products in the final reaction mixture.
The reaction conditions used seem to indicate the reaction was done under thermodynamic control. The reagents were stirred at room temperature for 5 hours, then irradiated with microwaves in 10 x 2minute bursts at 185oC. Thus, in order to investigate the reasons behind the observed product distribution, we should calculate the energies of the two products to determine whether the thermodynamically most stable product is the same as the observed predominant product in the reaction (7-fluoro product). This was done in two ways. Firstly, the structures were sent through a MM2 Forcefield energy minimization to determine their energies. Then once that was complete, the optimized structures were run on a PM6 method for energy minimization. It should be noted that the chiral centre present in the product molecules results in two enantiomers of each of the prodcuts causing 4 different products being formed. However, in this case, it is safe to ignore two of the enantiomers at this stage, as we can assume they will have almost identical energies (the enantiomers shall be investigated later). However, to make this assumption as safe as possible, we will consider the same enantiomer for each of the product, the case where the methyl is above the plane of the ring system. The results of the energy minimizations are given below.
A we can see from the calculated data, we seem to contradict ourselves. It seems that the reaction is done under thermodynamic conditions, however, both the MM2 and PM6 calculations imply that it is in fact the 5-fluoro product that is the most stable and hence the thermodynamic product, whereas, the experimental evidence seems to tell us that the 7-fluoro is the predominant product. This seems to tell us that the reaction is not under thermodynamic control, and is in fact under electrostatic control (in this case kinetic), so the initial attack occurs at the most electron rich position on the ring, and the reaction occurs via a non-reversible manner, so once the initial attack occurs to give a bias towards the 7-fluoro product the reaction is forced down one path way. This seems therefore to imply that the reaction stops at an intermediate stage during the 5 hours of stirring at room temperature, and the irradiation of microwaves and heating up to 185o degrees is to promote the Nazarov Cyclization forming the final products.
Characterisation of Products via Infra-red Spectroscopy:
The first analytical technique that could be used to differentiate between the products is IR spectroscopy. By simple observation of the molecules, we do not expect the IR spectra of the two regioisomers to be too different from each other, and, the IR spectra have not been reported in literature, however, for completeness sake at least, it is worth to predict these spectra to calculate what we would expect the spectra of the two isomers to look like in case it was decided that the compounds should be synthesised again, and the IR spectra of the purified products recorded to differentiate between the two.
IR Spectroscopy of 5-fluoro-3-methyl-1-indanone:
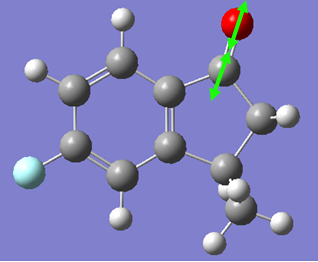
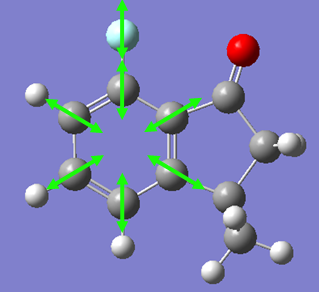
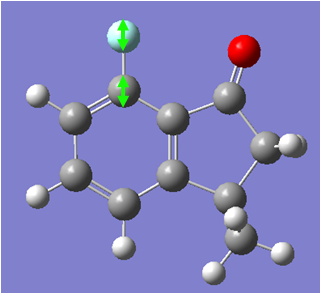
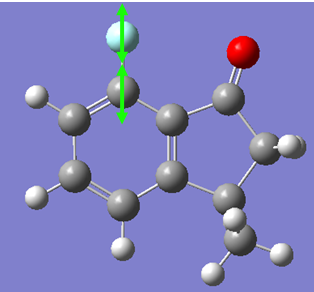
The IR spectrum of the compound was generated as follows. Firstly, the molecule's structure by performing both MM2 and PM6 energy minimizations. Then, a Gaussian calculation was set up to optimize geometry further and to generate the vibrational frequencies. the model used was B3LYP with the 6-31G(d,p) basis set. The results from the calculations can be seen below, with the spectra and the key vibrations picked out.
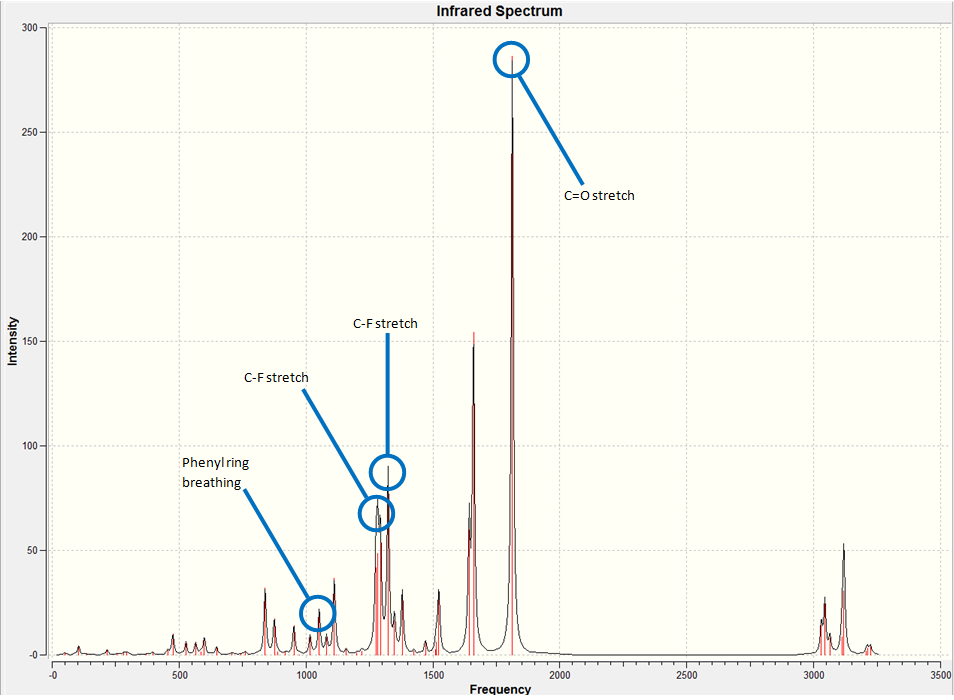
The data generated from the calculation gives us an indication of the bond strength of the various functional groups in the molecule. As expected, the C=O stretch gives an extremely large intensity due to the large change in dipole moment in the vibration (IR spectroscopy can be thought of as measuring changes of dipoles in a molecule at certain energies). These values now give us a benchmark with which to compare the energies of the vibrations in the 7-fluoro isomer. However, we would expect them to be similar.
IR Spectroscopy of 7-fluoro-3-methyl-1-indanone:
The IR spectrum of the compound was generated as follows. Firstly, the molecule's structure by performing both MM2 and PM6 energy minimizations. Then, a Gaussian calculation was set up to optimize geometry further and to generate the vibrational frequencies. the model used was B3LYP with the 6-31G(d,p) basis set. The results from the calculations can be seen below, with the spectra and the key vibrations picked out.
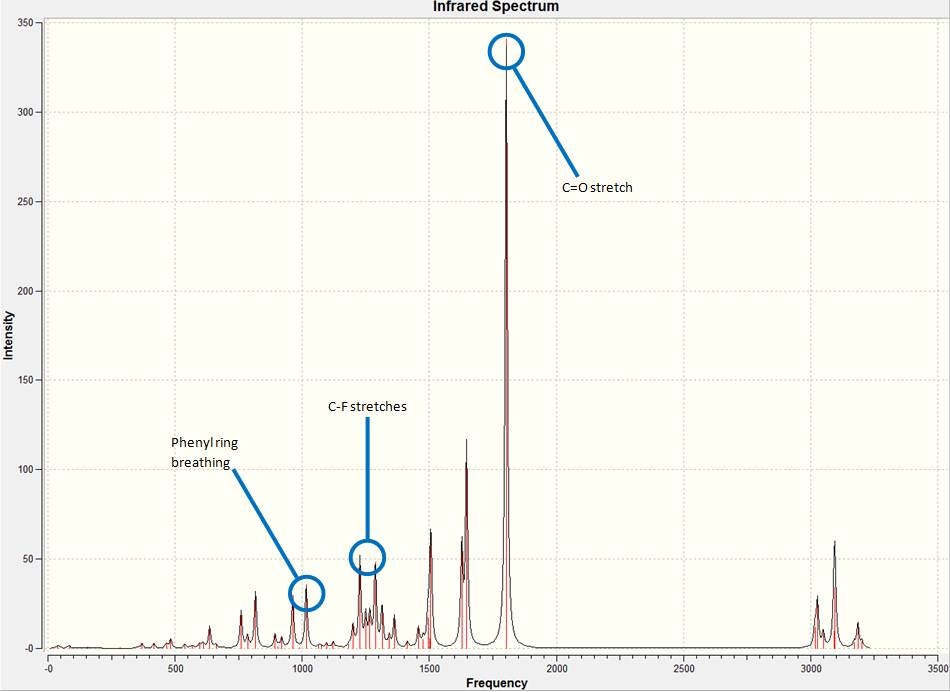
IR Spectroscopy Conclusion:
The data generated from the vibrational calculations is surprising. By inspection, it was expected that the IR spectra of the two compounds would be almost identical. This is true to a certain extent, however, by closer analysis of the data, it could quite possibly be done. All of the key vibrations of the molecule in the 7-fluoro compound occur at lower energies that their corresponding vibrations in the 5-fluoro compound. We also observe different patterns of intensities of the peaks in the spectra and also see a slightly different pattern to the peaks, especially in the range 1000-1500 cm-1. Although characterisation of the two isomers would be possibly be viable via analysis of the IR spectra, it would be extremely difficult, and there are other more straightforward techniques that could be used to differentiate between the two isomers.
Characterisation of Products via NMR:
In the literature, NMR spectroscopy was used to differentiate between the two isomers. Accordingly, calculations were set up in the Gaussian interface to predict both the 13C NMR and the 1H NMR of the two products. Although conventionally we are told to take computer simulations of the 1H NMR with "a pinch of salt(preferably sodium chloride)" in terms of the chemical shift values it predicts, in the case of the molecules analysed, the fit to the experimental data was in fact rather good, asd thus has been included in the report.
1H NMR of 5-fluoro Product:
The 1H NMR of the 5-fluoro product was predicted using a Gaussian calculation. The results and the spectrum generated are shown below.
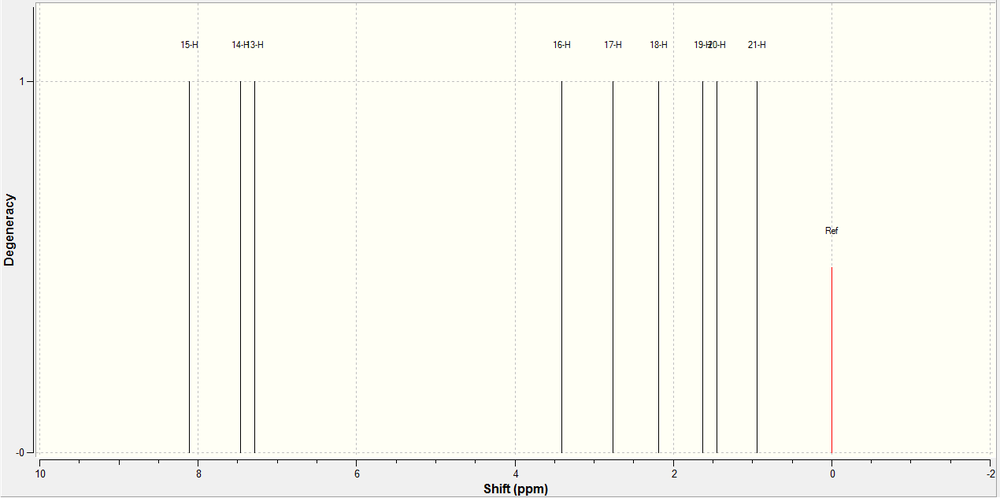
| Hydrogen | 1H Calculated | Schematic |
|---|---|---|
| ||
| Hydrogen | 1H Calculated | 1H Reported |
|---|---|---|
The calculation does not take into account rotations in the molecule, so in the real spectrum we observe time averaging between H21, H20 and H19 into 1 peak, and H13 and H14 although not 1 peak, would be so close in chemical shift, they would most probably be merged into one set of peaks. This is what is observed in the spectrum recorded in literature. We can then average these chemical shifts and compare these to what is recorded in literature and observe the correlation between the recorded spectrum and the calculated one. As we can see from the table above, there is a very good correlation between the calculated data and the experimental data.
13C NMR of 5-fluoro Product:
The 13C NMR of the 5-fluoro product was predicted using a Gaussian calculation. The results and the spectrum generated are shown below.
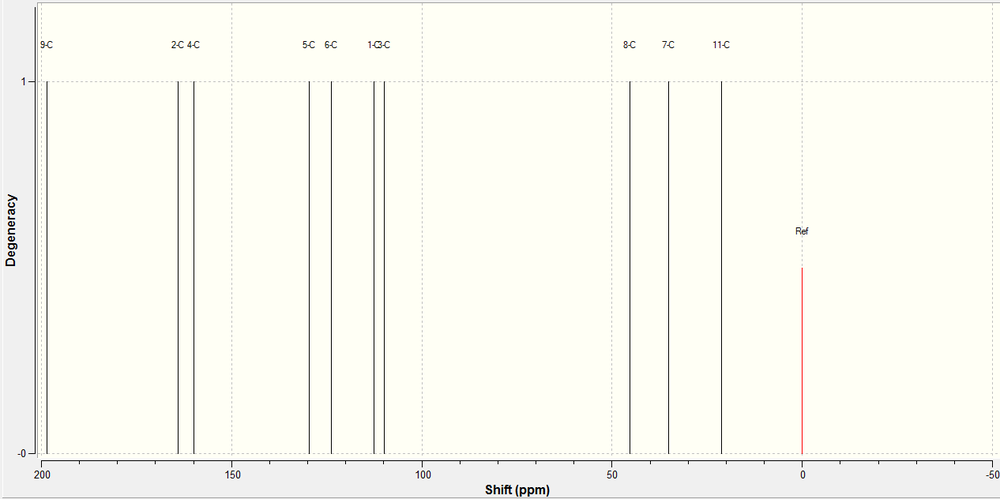
| Carbon | 13C Calculated | 13C Experimental | Schematic |
|---|---|---|---|
| |||
We very rarely observe degenerate carbon atoms in a 13C NMR as they are almost always in different environments to each other. This means that we observe a single peak per carbon in the spectrum, making it easier to analyse the spectra. As you can see from the data above, we get a good correlation between the calculated data and the experimental reported data. We have to understand that there is an intrinsic error in these type of NMR calculations, and this is magnified by the larger chemical shifts, however, we can still say confidently that the correlation between calculated and experimental results is good.
1H NMR of 7-fluoro Product:
The 1H NMR of the 5-fluoro product was predicted using a Gaussian calculation. The results and the spectrum generated are shown below.
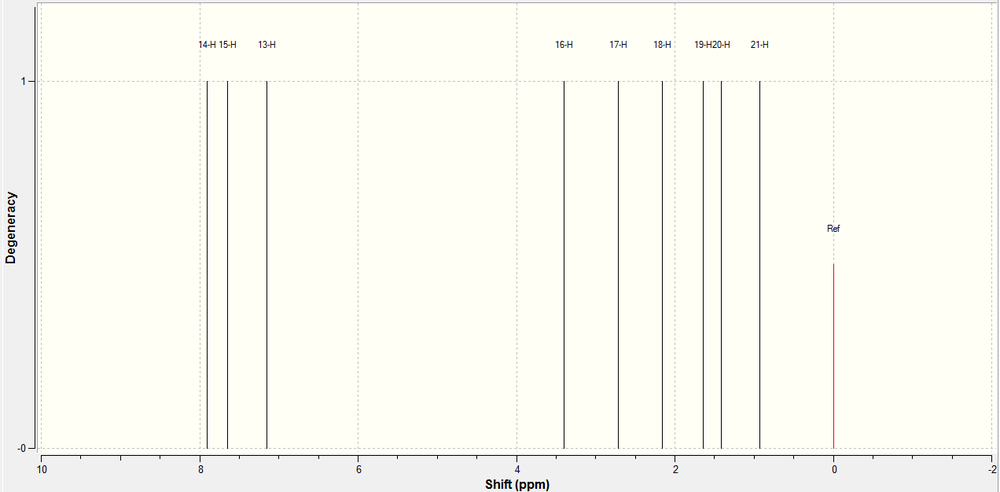
| Hydrogen | 1H Calculated | Schematic |
|---|---|---|
| ||
| Hydrogen | 1H Calculated | 1H Reported |
|---|---|---|
The calculation does not take into account rotations in the molecule, so in the real spectrum we observe time averaging between H21, H20 and H19 into 1 peak, and H13 and H14 although not 1 peak, would be so close in chemical shift, they would most probably be merged into one set of peaks. This is what is observed in the spectrum recorded in literature. We can then average these chemical shifts and compare these to what is recorded in literature and observe the correlation between the recorded spectrum and the calculated one. As we can see from the table above, there is a very good correlation between the calculated data and the experimental data.
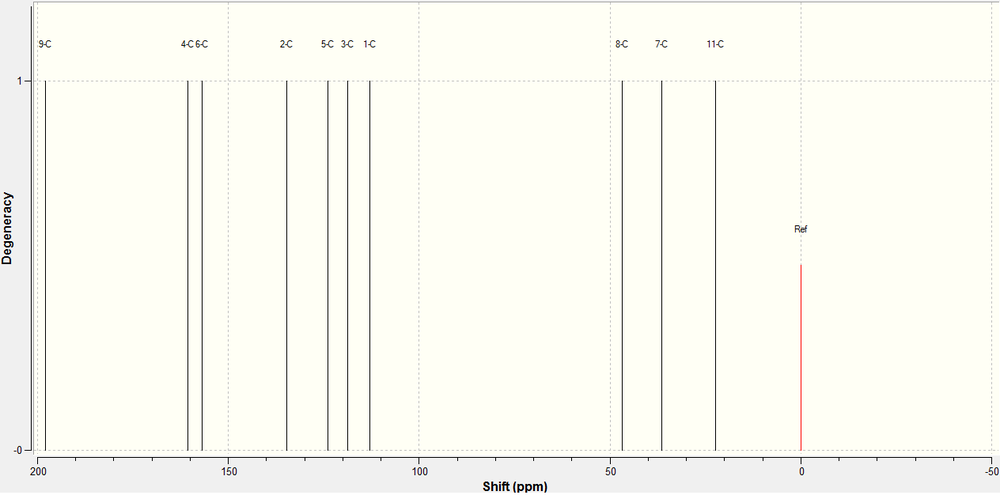
13C NMR of 7-fluoro Product:
The 13C NMR of the 7-fluoro product was predicted using a Gaussian calculation. The results and the spectrum generated are shown below.
| Carbon | 13C Calculated | 13C Experimental | Schematic |
|---|---|---|---|
| |||
We very rarely observe degenerate carbon atoms in a 13C NMR as they are almost always in different environments to each other. This means that we observe a single peak per carbon in the spectrum, making it easier to analyse the spectra. As you can see from the data above, we get a good correlation between the calculated data and the experimental reported data. We have to understand that there is an intrinsic error in these type of NMR calculations, and this is magnified by the larger chemical shifts, however, we can still say confidently that the correlation between calculated and experimental results is good.
NMR Spectroscopy Conclusion:
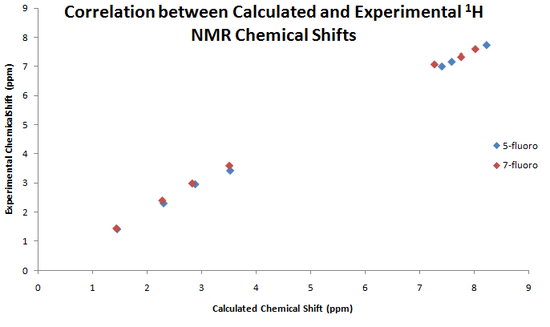
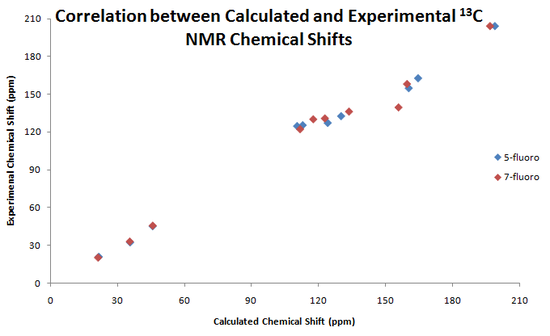
Below are presented graphs showing the correlation between the calculated and experimental chemical shifts of the 1H and 13C NMR.
 |
 |
|---|
As we can see from the data above, NMR would be a good choice to differentiate between the products. Using 13C NMR would be a better choice than 1H NMR as there are more obvious differences between the spectra for the 5-fluoro and 7-fluoro products. The 13C NMR calculation gives values with an error of approximately 3-5ppm, but still, even considering this, the calculations still agree with the data given in the original paper.
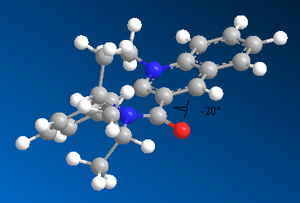
Characterisation of Products via Optical Rotation:
Again, although the optical rotation was not quoted in the literature, it was still calculated for completeness sake. This way, if the rotation was ever measured, we could have an expected value, and also, perhaps once purification was carried out on the products, they could be characterised using the results from the optical rotation.
| Isomer | Enantiomer | Optical Rotation |
|---|---|---|
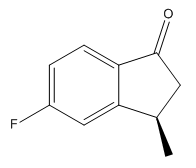 |
||
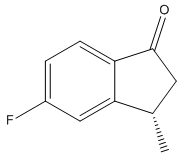 |
||
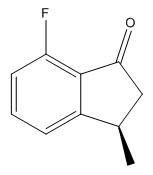 |
||
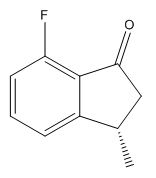 |
The values of the optical rotation calculations give very small angles. These are probably too small to be used to characterise the products, as we would classify a reasonably sized rotation somewhere in the region of 100o. What is interesting though is the signs of the optical rotation for corresponding enantiomers. In the cases where the two methyl groups are on the same side of the ring, we observe optical rotations of different signs. We can rationalise this by considering the dipole moments of the two products. Light has both electronic and magnetic contributions, and would therefore interact with different dipoles in different ways. The dipoles of the 5-fluoro and 7-fluoro products are 2.69D and 4.59D respectively (taken from the output file of the Gaussian geometry optimization calculation). As the dipoles are so different, we would observe different interactions of light with the two molecules, and hence the radically different optical rotations.
Conclusion:
In conclusion, we can confidently say that the NMR assignment of both the 1H and 13C spectra are correct. We have also seen the possibility of using either IR spectroscopy or Optical Rotation to differentiate between the two products. In the case of IR, the spectra do show slightly different patterns in the region between 1000-1500 cm-1, however, the differences are marginal, and in the case of an actual spectra being recorded these could be absorbed into noise or slight inaccuracies in the recording of the spectrum. Therefore, we can discount IR spectroscopy as a valid technique to differentiate between the products. In the case of optical rotation, again, there are noticeable differences between the two isomers, however, again, the actual reading is so small, experimentally determining them would result in large errors. We can therefore discount optical rotation to differentiate between the two products, but it could be used to determine the relative amount of enantiomers made in the reaction due to the difference in the sign for the corresponding enantiomers of the 5- and 7-fluoro products. Therefore, in conclusion, we can say that the use of NMR was most probably the best way to differentiate between the two products due to the significant differences in the spectra of the two products.
References:
- ↑ N.Allinger, J. Am. Chem. Soc., 1977, 99(25), pp 8127–8134:DOI:10.1021/ja00467a001
- ↑ J. Chem. Phys., 2005, 124:DOI:10.1063/1.2148954
- ↑ R.Jarret, J.New, R.Hurley & L.Gillooly J. Am. Chem. Soc. 2001, 78 pp1262:DOI:10.1021/ed078p1262
- ↑ Clayden, Greeves, Warren & Worthers Organic Chemistry 2008 7th Edition pp912-916
- ↑ A.Schlutz, L.Flood, J.Springer, J. Org. Chem., 1986, 51 (6), pp 838–841:DOI:10.1021/jo00356a016
- ↑ Chem. of Hetrocyclic Compounds, 1994, 30(11-12), pp 1331–1385:DOI:10.1007/BF01172864
- ↑ W.Maier, P.Schleyer, J. Am. Chem. Soc., 1981, 103, pp 1891–1900:DOI:10.1021/ja00398a003
- ↑ G.Buchanan, G.Jamieson, Tetrahedron, 1972, 28 (4), pp 1123-1127:DOI:10.1016/0040-4020(72)80172-8
- ↑ W.Yin, Y.Ma, J.Xu, Y.Zhao, J. Org. Chem., 2006, 71 (11), pp 4312–4315:DOI:10.1021/jo060022p