Jump to content

Rep:Mod:rt90

From ChemWiki

Module 3a: The Cope Rearrangement Tutorial


Introduction

The aim of this module was to characterise the transition structures on potential energy surfaces, for two reactions using computational chemistry. The Cope rearrangement and the Diels Alder cycloaddition, which was under investigation, are larger systems than ones where specific formulae can be applied to solve the energy and the structural determination cannot be calculated easily using molecular mechanics/force field methods. This is because they do not consider changes in bonding type/electronic distribution, and what bonds are being made/broken. Molecular orbital-based methods are used; these solve the Schrodinger equation numerically and use the local shape of a potential energy surface to locate a transition state structure. Barrier heights and reaction paths can also be calculated using this method.

Optimizing the reactants and products

Cope rearrangement
Anti-3
Gauche-3
Anti-2

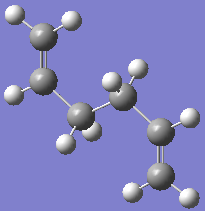
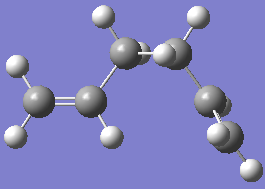
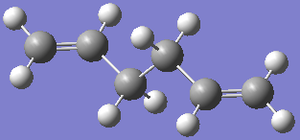
The first reaction under investigation is the Cope rearrangement of 1,5-hexadiene, shown left. This [3,3]-sigmatropic shift rearrangement goes through a chair or boat transition state, although the later is higher in energy. In the past this reaction has been the centre of controversy, however computational chemistry allows us to predict the stability of the transition states. Good experimental agreement has been obtained using the method described below. The transition states were be drawn out using Gaussview, the structures optimised to obtain a minimum, symmetrised for the point group and the vibrational frequencies calculated and viewed. These results were then compared with literature.

A molecule of 1,5-hexadiene with anti-periplanar confirmation was drawn - as there are 4 possibilities 'anti-3' from Appendix 1[1] was chosen. The structure was cleaned to tidy up the different bond lengths and angles and the structure was optimised - method: Hartree-Fock, basis set: 3-21G, %mem 250MB, changed under the Link 0 tab. Once complete the .chk file was downloaded for analysis[2]. The final structure has symmetry, more specifically its point group is C2h symmetry, found by looking at Edit->Symmetrize and the energy/Hartree is -231.68907. This data matches what is in the appendix.

A gauche confirmation, number 3, was then chosen out of the 6 possibilities and optimised in the same way[3](the file was originally on SPECRa but was accidently deleted). The point group is C1 and the energy/Hartree -231.69081 - the point group matches what is in the appendix and the energy is extremely close. The gradient is again close to 0, but less so than the previous structure. It is expected and was found that the Gauche conformer would be higher in energy because, in this conformer the alkene groups are next to each other in the Newman projection. In the anti-periplanar conformation they are opposite each other, this reduces the steric clash between the electron dense orbitals of the alkenes, hence bringing its energy down. Based on the results obtained, the gauche-3 conformer is slightly more stable than the anti-3 conformer. This can be explained by considering σ C-H and π* C=C the interactions, which result in more stabilisation than the steric clash between the C=Cs, hence bringing its energy down.

Based on this, it was predicted that the lowest energy conformation of 1,5-hexadiene would be gauche-1. The structure was drawn out and optimised; the point group was found to be C2 and the energy/hartree -231.6872. The anti-2 conformer was then drawn, it had Ci symmetry and an energy/hartree -231.69254 which is again the same as that given in appendix 1. As visually and numerically it is confirmed that the structures are the same, the molecule was optimised again - method: B3LYP, basis set: 6-31G*(/6-31G(d))[4]. The point group remained the same, however there was a reduction in energy/hartree to -234.61172 because this uses a more accurate basis set than the previous method. A minor change in geometry was also noted, as the bond angles between the alkane linkages(middle atoms) was 111.3o, now 112.7o and the alkene/alkane linkages(end 3 atoms) 124.8o to 125.3o. The alkene bond lengths increased from 1.316Å to 1.334Å, whereas the alkane bond lengths slightly decreased from 1.509 and 1.553Å to 1.504 and 1.548Å. The HF/3-21G calculation therefore underestimates the bond length for alkenes, overestimates the bond lengths for alkanes, and underestimates the bond angles.

The B3LYP/6-31G* of the anti-2 conformation was then used to run frequency calculations at the same level of theory. This is because the final energies from optimisation are based on the energy of the molecule on the bare potential energy surfaces. By ensuring that the vibrational frequencies are real and positive, we can confirm that the transition state is at a minima (te critical point). Additional calculations and terms need are used in this calculation, and thus allow for comparison with the literature.

IR spectrum

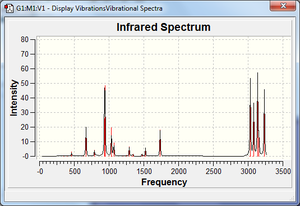
Once the job was finished the summary file was checked to ensure we still had the same molecule, as the energy was the same we did[5]. The vibrations were then checked - this showed all positive and no imaginary frequencies. The IR spectrum on the left shows both C-H alkane and C-H alkene vibrations, as expected. The file was then viewed and the following thermochemistry data was extracted: 

- Thermochemistry -
-------------------
Sum of electronic and zero-point Energies=           -234.469188
Sum of electronic and thermal Energies=              -234.461839
Sum of electronic and thermal Enthalpies=            -234.460894
Sum of electronic and thermal Free Energies=         -234.500773



The first sum is the potential energy at 0K, this value includes the zero-point vibrational energy, the second is the energy under standard conditions (298.15K and 1 atm - rotational, vibrational and translational contributions), the enthalpy of this incorporates RT and the final term looks at this and the entropic contribution. The sum of electronic and zero-point energies was compared to the literature value of -234.3287[6];. This value is slightly higher than the literature value by 0.140488 hartree, which considering the same methods are being used, is a higher difference than expected.

Optimizing the "chair" and "boat" transition structures

Chair TS optimisation 2
Chair TS optimisation 3

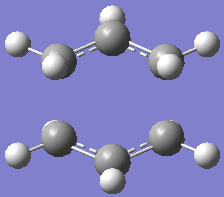
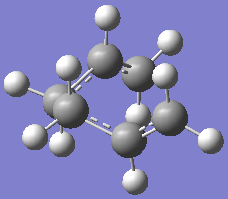
The main ways in which the transition state of these structure was optimised was by computing the force constants at the start of the calculation, using a redundant coordinate editor and using a new method QST2. Activation energies for the Cope rearrangement via these transition structures were also calculated and the IRC (intrinsic reaction coordinate) was run. As both of these structures are made up of 2 C3H5 fragments, of different symmetry (C2h and C2v), a fragment was drawn and optimised using HF/3-21G.

Chair: As the optimised structure looked like one half of the structure in appendix 2[7], 2 of these fragments were orientated so they looked like the chair transition state given and were approximately 2.2Å apart. The transition state was then optimised manually, which relies on knowing the reaction coordinate and having a good guess for the transition state geometry to work. The following parameters were selected - job type: Opt+Freq, optimise to a: TS (Berny), calculate force constants: once, method: HF, basis set: 3-21G and additional keywords: Opt=NoEigen, which prevents the calculation crashing if there is an imaginary frequency present. At 818cm-1 an imaginary frequency was found which corresponded to the Cope rearrangement and the energy/hartree was -231.3501[8].

The structure was optimised again using the frozen coordinate method (optimisation 2, left). The redundant coord editor was used on the one terminal carbon from each fragment that would form/break a bond during this process - bond and freeze coordinate were selected. This process was repeated with the other 2 terminal carbon atoms. The structure was minimised using job type: optimisation and HF/3-21G theory, although Opt=ModRedundant was left in additional keywords. The result looks the same as the previous method, except that the bond forming/breaking distances are now fixed at 1.803Å and the energy/hartree has decreased slightly to -231.6103.[9]. These distances were now optimised (optimisation 3, right) using the redundant coord editor again and making new coordintes. This time, freeze coordinate was not chosen, instead derivative was selected. The transition state optimisation was used again - everything was kept the same except calculate the force constants was left as never. It was found that the distance between two of the terminal C atoms has significantly changed and both are different at 1.55 and 4.39Å and the energy/hartree again fell, but by less this time to -231.6917[10]. The bond angle between the carbons has also changed from 118.3o to 125.0o. This is because the restriction on these distances has been removed and so the molecule bends to a new transition state minima.

Boat TS pre-optimisation
Boat TS optimisation

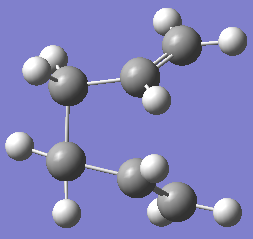
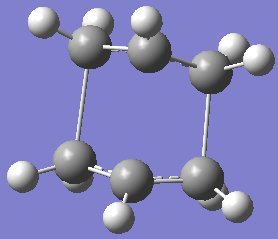
Boat: This structure was optimised using the QST2 method because the reactants and products could be stated; from this the calculation works out the transition state between the two structures. The anti-2 structure was again used, on this the numbering of the atoms was changed manually on the product to match the reactant. When Gaussian was run - job type: opt + freq, optimise to: TS (QST2). This failed because rotation around the central bonds was not considered during optimisation. This had to be done manually by changing the dihedral angle to 0o and the angle between the inside carbons to 100o. This time the job was successful and there was only one imaginary frequency at 1154cm-1 and its energy/hartree was -231.5254[11]. This method is only reliable when the reactants and products are close to the transition state, therefore the QST3 method can be used instead. The optimised chair structure looks like 2 of the anti-2 conformers of 1,5-hexadiene, whereas the boat structure looks similar to gauche-3.

The IRC (intrinsic reaction coordinate) method was then carried out on an optimised chair structure so the minimum energy path from a transition state to the local minimum on a potential energy surface could be followed. Small geometry steps are calculated in the direction where the slope of the energy surface is steepest, going down to a minimum. From Gaussian - job type: IRC, follow IRC: forward direction, calculate force constants: once, compute more points: N=50 so that more points are considered along the IRC. The bond distance between the terminal carbons was 1.975Å, although the geometry is still not at a minimum. The forces were therefore computed at every step - whilst this is the most reliable method it cannot be carried out on large systems because it is expensive. The bond distance was 1.803Å[12], which is the same as the value obtained in the previous optimisation.

The activation energy for both transition structures was calculated by reoptimising the structures differently - method: B3LYP, basis set: 6-31G*, starting from the HF/3-21G optimised structures. For the chair - energy/hartree: -234.5587, bond distance between terminal carbons: 1.554Å and 4.536Å[13],. The bond distances are similar to the other method, however the energies are lower because it is a different method of optimisation. The same can be found with the optimised boat, where the energy is: -234.5593.

If we look at the activation energy the experimental ones are 33.5±0.5kcalmol-1 chair, and 44.7±0.5kcalmol-1 boat at 0K. From the thermochemistry data, the activation energy for the chair was - 33.95 (0K) and 33.69kcalmol-1 (298.15K), whereas for the boat - 42.17 (0K) and 41.32 (218.15K). Both values are quite close to the literature, which reflects the fact a better basis set was used.

Module 3b: The Diels Alder Cycloaddition

Introduction

Diels Alder cycloaddition 1
Diels Alder cycloaddition 2

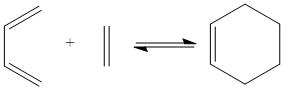
The transition states and shapes of the molecular orbitals for the Diels Alder cycloaddition (4s + 2s pericyclic reaction) was examined in this section. The bonds are formed when the π orbitals of the dieneophile interact with the π orbitals of the diene. When this happens the HOMO/LUMO on each reactant can interact to give a bonding and anti-bonding MO. The reaction is allowed when they do overlap, but if they have different symmetrical properties then the reaction is forbidden because overlap is not possible. Two cases were looked at - where the diene and edienophile were substituted and unbsubstituted, as the former results in secondary orbital effects. The orbitals can be labelled as symmetric or anti-symmetric - the HOMO of ethylene and the LUMO of butadiene are symmetric, whereas LUMO of ethylene and the HOMO of butadiene are anti-symmetric. The resultant adduct, which has 2 new σ bonds is anti-symmetric.

Cis-butadiene + ethylene transition structures

To begin with cis-butadiene was drawn out and Gaussian used to optimised its structure - method: HF, basis set: 3-12G[14]. In order to compute the transition state geometries, ethylene was also optimised the same way using Gaussian[15] and the product cyclohexene[16]. The HOMO and LUMO orbitals were visualised and the relevant data has been given below.

tr>
HOMO cis-butadieneLUMO cis-butadieneHOMO ethyleneLUMO ethylene
Orbital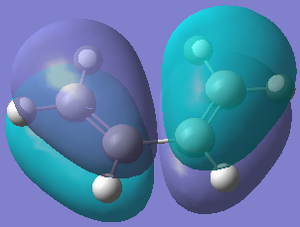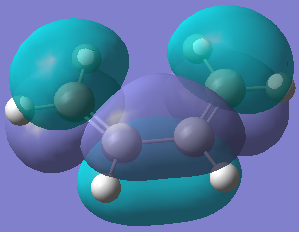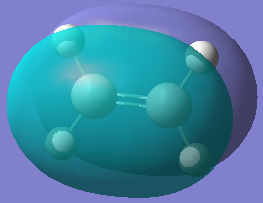
Energy/hartree-0.3430.017-0.3690.177
SymmetryAnti-symmetricSymmetricSymmetricAnti-symmetric


HOMO cyclohexneLUMO cyclohexene
Orbital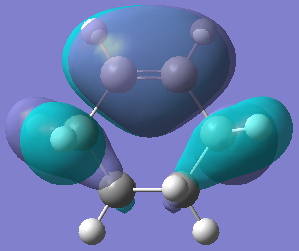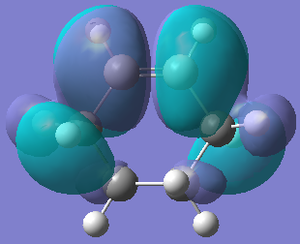
Energy/hartree-0.3420.198
SymmetrySymmetricAnti-symmetric



The two fragments were then orientated so they resembled the product, with each of the terminal C atoms being set approximately 2.2Å apart. The QST2 method outlined above was then used by correctly orientating and number the reactants and products. The HOMO and LUMO of the transition state orbtials were plotted and the relavent data has again been given below[17].

HOMO TSLUMO TS
Orbital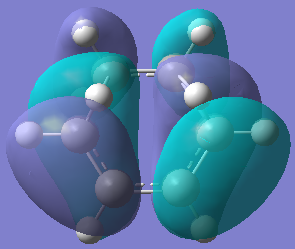
Energy/hartree-0.3020.142
SymmetryAnti-symmetricSymmetric



TS vibration

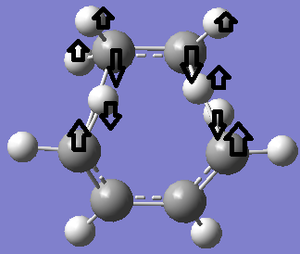
The bond lengths of the partly formed σ C-C bonds is 2.209Å. Typical sp3 C-C bond lengths are 1.54Å, whereas sp2 is 1.5Å[18] and the C van der Waals' radius is 1.70Å[19]. The bond length of the partially formed σ C-C bonds is not close to any of these, in fact it is much longer, which indicates that the molecule is in a transition state and is between the bond forming and breaking process. The vibrations that correspond to the reaction path at the transition state are shown on the left - the imaginary frequency was at 818cm-1 and shows that the formation of the two bonds is synchronous because the arrows move in the same direction. However, the lowest positive frequency at 167cm-1 is asynchronous because they move in different directions. The HOMO from butadiene and the LUMO from ethylene are used in the formation of the transition state MO because they are both anti-symmetric. They therefore have the same symmetry and as a result the reaction is allowed.





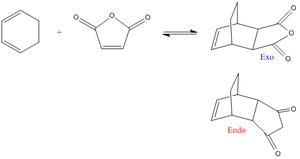
Cyclohexa-1,3-diene + maleic anhydride transition structures

To begin with the structures of cyclohexa-1,3-diene and maleic anhydride were drawn out and optimised using job type: optimisation, method: HF, basis set: 3-12G. The orbitals were then analysed - cyclohexa-1,3-diene[20]; maleic anhydride[21].

HOMO cyclohexa-1,3-dieneLUMO cyclohexa-1,3-dieneHOMO maleic anhydrideLUMO maleic anhydride
Orbital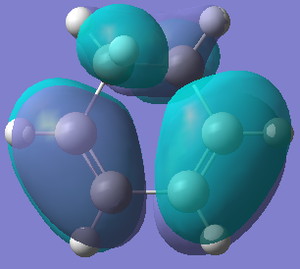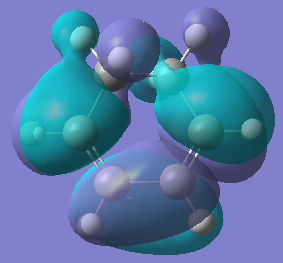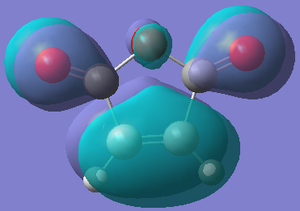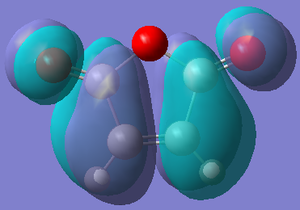
Energy/hartree-0.3020.136-0.3690.177
SymmetryAnti-symmetricSymmetricSymmetricAnti-symmetric



Exo product: The two fragments were then orientated so they resembled the product, with each of the terminal C atoms being set approximately 2.1Å apart. Transition state optimistion was run on the system - job type: opt+freq, optimise to a: TS(Berny), calculate force constants: once, method: HF, basis set: 3-12G. More details about this method are outlined above. The .chk file is analysed in more detail below[22]. Scans were run on the endo product, but there were problems in getting it working and eventually the scans returned the exo product again.

HOMO exo-productLUMO exo-product
Orbital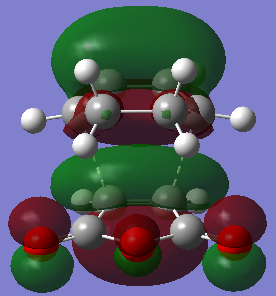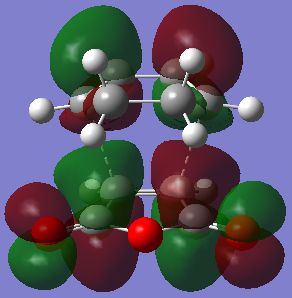
Energy/hartree-0.3550.058
SymmetrySymmetricAnti-symmetric



The bond lengths of the partly formed σ C-C bonds for the endo-product is 2.836Å.

References

  1. ↑ ChemWiki appendix 1, http://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Appendix_1
  2. ↑ Anti-3 optimisation, SPECRa Chemistry Repository: Item 10042/to-6201, DOI:10042/to-6201
  3. ↑ Gauche-3 optimisation, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:Gauche3.fchk‎
  4. ↑ Anti-2 optimisation, SPECRa Chemistry Repository: Item 10042/to-6204, DOI:10042/to-6204
  5. ↑ Anti-2 frequency, SPECRa Chemistry Repository: Item 10042/to-6205, DOI:10042/to-6205
  6. ↑ O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10336. DOI:10.1021/ja00101a078
  7. ↑ ChemWiki appendix 2, http://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Appendix_2
  8. ↑ Chair TS optimisation + frequency, SPECRa Chemistry Repository: Item 10042/to-6208, DOI:10042/to-6208
  9. ↑ Chair TS optimisation, SPECRa Chemistry Repository: Item 10042/to-6209, DOI:10042/to-6209
  10. ↑ Chair TS optimisation + frequency 2, SPECRa Chemistry Repository: Item 10042/to-6213, DOI:10042/to-6213
  11. ↑ Chair TS optimisation + frequency 2, SPECRa Chemistry Repository: Item 10042/to-6214, DOI:10042/to-6214
  12. ↑ Chair IRC, SPECRa Chemistry Repository: Item 10042/to-6228, DOI:10042/to-6228
  13. ↑ Chair optimisation, SPECRa Chemistry Repository: Item 10042/to-6229, DOI:10042/to-6229
  14. ↑ Cis-butadiene optimisation, SPECRa Chemistry Repository: Item 10042/to-6242, DOI:10042/to-6242
  15. ↑ Ethylene optimisation, SPECRa Chemistry Repository: Item 10042/to-6242, DOI:10042/to-6242
  16. ↑ Cyclohexene optimisation, SPECRa Chemistry Repository: Item 10042/to-6299, DOI:10042/to-6299
  17. ↑ Diels Alder optimisation, SPECRa Chemistry Repository: Item 10042/to-6300, DOI:10042/to-6300
  18. ↑ M. A. Fox, J. K. Whitesell, Organische Chemie., 1994, Specktrum
  19. ↑ A. Bondi, J. Phy. Chem., 1964, 68, 441. DOI:10.1021/j100785a001
  20. ↑ Cyclohexa-1,3-diene optimisation, SPECRa Chemistry Repository: Item 10042/to-6295, DOI:10042/to-6295
  21. ↑ Maleic anhydride optimisation, SPECRa Chemistry Repository: Item 10042/to-6293, DOI:10042/to-6293
  22. ↑ Exdo product optimisation, SPECRa Chemistry Repository: Item 10042/to-6311, DOI:10042/to-6311
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:rt90&oldid=820690"