Rep:Mod:rt60

Module 1a: Structure and Spectroscopy

The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

Introduction

Molecular modelling can be used to predict the structure and reactivity of organic compounds of known, as well as unknown reactions. The examples that follow provide an insight into what molecular modelling is capable of. The molecular mechanics methods implemented involve the general procedure of optimising a molecule's molecular geometry so that its energy is at a minimum, relating this energy to a factors such as angle strain, bond length, van der Waals' forces and steric effects.

The model is however limited because is is based on experimental data of known molecules. The kinetics of a reaction are therefore very difficult to predict because the structure and energy of the transition state would have to be known. Molecules with certain functional groups, metal ions or those which have unusual bonding cannot be modelled with this method, therefore the quantum mechanical treatment has to be used. The same problem applies to ones that are aromatic, hyperconjugated and/or have stereoelectronic effects because the electronic distribution of the molecule would be required.

The programme used to carry out these calculations is ChemBio3D - in particular the Allinger MM2 molecular mechanics model.

The hydrogenation of cyclopentadiene dimer

Exo product

Hydrogenation product 1

Endo product

Hydrogenation product 2

1,3-Cyclopentadiene, which can be formed from dehydrocyclisation of 1,3-pentadiene , will slowly dimerise at room temperature to give two isomers. Preferentially, the endo product is formed over the exo product in an intermolecular Diels-Alder reaction. Whilst the exo product was found to be lower in energy, 31.9kcal mol^-1 exo vs 34.0kcal mol^-1 endo, and is therefore the thermodynamically more stable product, the endo product is formed faster. Our results also show that the endo-product has more strain in the system, shown by the increased torsion energy in the endo product, 7.67kcal mol^-1 exo vs 9.51kcal mol^-1 endo. However, what the model cannot rationalise is that the p-orbitals on the substituents of the dienophile overlap with the p-orbitals on the diene in a favourable interaction, which stabilises, what appears to be in terms of numbers, the "unfavourable" product. The reaction is therefore kinetically controlled, favouring kinetics over thermodynamics. Whilst the reaction is reversible, the activation barrier to the reverse process is high enough that over time, the thermodynamic product does not form and thus predominate.

The endo product can then be hydrogenated to give two products. Various energies for each product, given below in kcal mol^-1, were then analysed in order to investigate which is more stable. It can be seen from the data below most of the energies are fairly similar, apart from the bending energy, which is the largest contributor to the difference in total energy. Hydrogenation product 2 will be formed over 1 because it is the more stable, as its total energy is lower. This is backed up by comparing the total energy of the endo product to these two energies - hydrogenated product 1 would result in an increase in total energy, which is unfavourable, especially given that product 2 decreases the total energy of the system. Whilst now similar, both torsion energies are now higher, reflecting increased strain in the system. For product 1, this is compensated for in other ways.

	Stretching	Bending	Torsion	Van de Waals	Dipole-dipole	Total energy
Product 1	1.23	18.7	12.8	6.04	0.38	36.9
Product 2	1.12	13.0	12.4	4.44	0.45	29.6

Stereochemistry of nucleophilic additions to a pyridinium ring (NAD+ analogue)

Reagent 1

Reagent 2

Product 1

Product 2

The optically active derivative of prolinol was investigated first. It was found that when the energies were minimised in the MM2 force-field, the energy values given in the table below were obtained, in kcal mol^-1. The MeMgI component could not be included in the calculation because the programme gives a warning, stating that 'No atom type was assigned to the selected atom' when attempts are made to minimise the energy. The reaction is highly stereo- and regioselective, therefore MeMgI reacts predominantly para to the positive nitrogen atom as opposed to ortho. This is because MeMgI coordinates to the carbonyl oxygen, directing the Me group and thus attack onto the para position. The geometry of the carbonyl group favours this process because it is angled towards the pyridine ring. Whilst attack can occur above or below the plane of the ring, it was found that the lowest possible conformation is the one shown left.

The second reagent reagent to be investigated is shown right, which is reacted with aniline. Again energy values obtained for the lowest energy configuration have been given in the table below in kcalmol^-1. The reaction is again highly selective, forming a single disteroisomer with >95% yield. The amine reacts on the opposite face to the carboyl lactam, such that attack is directed again onto the para position in relation to the N+ ion. The attack is initiated by the lone pair on the N atom of aniline, which is directed into this plane of attack by the carbonyl group, as in the previous example. The chiral axis defined by the carbonyl is the main reason for the high (diastereofacial) selectivity seen in the molecule.

These models can be improved by implementing the quantum mechanical approach on the system, most importantly, taking into account molecular orbital theory. As stated before, this molecular mechanics model is based on experimental data and makes a number of key simplifications; namely it does not consider the electronic distribution in the molecule (aromaticity, frontier orbital interactions, etc). Also, MeMgI could not be taken into account in the first system, since metal ions can normally not be processed by the system.

	Stretching	Bending	Torsion	Van de Waals	Dipole-dipole	Total energy
Reagent 1	2.04	14.2	5.22	16.5	-3.98	43.2
Reagent 2	3.96	11.7	9.72	29.3	-4.88	63.4

ChemBio3D has a bug which affects the molecular mechanics force field when applied to the N+ atom. As a result, the calculations were repeated using the MOPAC molecular orbital method, as the bug affects the energy and geometry values obtained. The PM6 method was specifically chosen; the results of the calculations are given below. The total energies are considerably higher than that obtained from the MM2 method, indicating that the systems are less stable than previously thought. This also highlights the extent of the error. The geometry of the molecule was also looked at by analysing the dihedral angle between the carbonyl group and the aromatic ring. The dihedral angle much larger for the second reagent compared to the first, which can be seen when looking at the molecule. It is considerably distorted, backing up the idea that there is more strain in the molecule resulting in a higher energy. However, these angles are still considerably lower than 90°, which reflects the fact the carbonyl group directs incoming nucleophilic attack.

	Heat of formation/kcal mol-1	Dihedral angle/°
Reagent 1	93.9	20°
Reagent 2	156	45°

Stereochemistry and reactivity of an intermediate in the synthesis of Taxol

Isomer 1a

Isomer 2a

Isomer 1b

Isomer 2b

The intermediate in the total synthesis of Taxol can have two configurations, the carbyonyl group can either face up or down. Both of these isomers were investigated to determine which was more stable. The energies obtained, in kcalmol^-1, when the MM2 force-field was run are given below - the alkene isomers have been labelled 'a'. It is clear from the data that the first isomer, in which the carbonyl group is pointing up, is more stable. There is less steric clash between the carboyl and neighbouring groups when it is in this configuration, which is backed up by the data as the van der Waals' interaction is lower. The bending energy and stretching energies are also lower, implying that isomer 1a is closer to the ideal energy than 2a. Finally, the torsion energy is slightly higher for isomer 2a, meaning that there is more strain in the system.

Upon hydrogenation of both isomers, both isomers have a resultant increase in the total energy; they have been labelled 'b'. This suggests that the alkene is more stable than the alkane, which can be explained by looking closer at the specific energies. For both hydrogenated products, the stretching energy is higher, so the bond lengths are even further away from what is ideal, resulting in increased strain on the molecule. The bending energies are also higher for both the hydrogenated prodcuts (and when comparing isomer 1 to isomer 2), which suggests that the bond angles are much more distorted compared to the equilibrium bond angels. Whilst the torsion energies are similar, they are still somewhat raised, again indicating that there is increased strain on the molecule. Finally the van der Waals' forces are (almost) zero, suggesting that the attraction between molecules, and again their stability, has decreased. The reasons for all the rise in repulsion and the reduction in stabilisation is due to the extra electron density in the molecule. The addition of two hydrogen atoms in a tertiary and secondary position (the former being more important) will cause an increase in steric clash between orbitals, which distorts the molecule and brings it further away from ideality. Overall, we can attribute the decrease in stability going from the alkene to alkane to alkene hyberstability.

	Stretching	Bending	Torsion	Van de Waals	Dipole-dipole	Total energy
Isomer 1a	2.55	10.7	19.6	12.5	-0.181	44.3
Isomer 1b	3.08	16.5	22.4	15.3	0.00	58.0
Isomer 2a	2.78	16.4	21.4	14.1	0.14	54.4
Isomer 2b	5.07	27.0	23.5	20.1	0.00	79.0

The isomers were also optimised using the MMFF94 force-field, but this only gives a value for the total energy, as opposed to a breakdown of the individual components. It can be seen in the table below that these energies, in kcal^-1 show the same relationship in terms of stability as the MM2 energies. The values are however considerably higher because this force-field performs calculations on a broad set of molecules, as opposed to specific ones such as small molecules. The accuracy of this model is therefore likely to be lower in this case.

	Total energy
Isomer 1a	60.6
Isomer 1b	76.3
Isomer 2a	80.5
Isomer 2b	114.8

Modelling using semi-empirical molecular orbital theory

HOMO

LUMO

HOMO-1

LUMO+1

LUMO+2

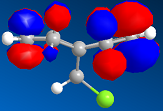
This section moves on from the classical treatment of a molecule to the more advanced quantum mechanical approach. In order to do this, the geometry of the molecule needs to be established by minimising the energies again. The total energy of the molecule calculated using the MM2 approach was 17.9kcal mol^-1. The MOPAC/PM6 method was gave a relatively similar value of 19.7kcal mol^-1 for the heat of formation, so the MM2 method is reasonably accurate for this molecule. The latter method, however, is an approximate representation of the valence-electron molecular wavefunction; more specifically of the HOMO which is reactive towards electrophiles. Rotation is restricted around the carbon upon which the Cl and H atom reside, so the two alkenes are different. We can deduce that the alkene furthest away from the Cl atom will be the more reactive of the two because, for an incoming nucleophile there is less steric hinderance on this face because the H atom is much smaller, and therefore electron rich, than the Cl atom. This double bond is the most nucleophilic.

The model backs this prediction up when we investigate the HOMO, HOMO-1, LUMO, LUMO+1 and LUMO+2 molecular orbtials, shown to the sides. Firstly, it shows that our model does distinguish between the two alkenes. From this we can see that there is a build of electron density anti to the Cl atom on the LUMO, whereas on the HOMO this build up is syn to the Cl atom, so the alkene anti to the Cl atom will be attacked.

When the double bond anti to the Cl atom is hydrogenated, the MM2 force field shows that the energy is raised to 22.4kcal mol^-1, suggesting the alkene is more stable than the alkane. However, the MOPAC/PM6 method gives a negative heat of formation value, -2.43kcal mol^-1. If we break down the energy values for each of the systems further using the MM2 method, we can see where there is stability in each molecule. The stretching energies are very low for both, so the current bond lengths are quite ideal; strain on both molecules from this contributer is very low. The bending energies are slightly higher, but again both are similar so comparisons cannot be drawn here. The torsion energies are both raised, but the alkene more so which shows that there is increased strain in the molecule. The dipole-dipole interactions are also more favourable in the diene. This ultimately suggests that the diene is more stable.

	Stretching	Bending	Torsion	Van de Waals	Dipole-dipole	Total energy
Diene	0.63	4.80	7.62	5.78	0.11	17.9
Alkene	0.88	4.69	10.8	7.04	0.07	22.4

IR diene

IR alkene

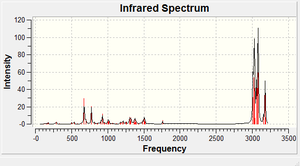
The IR spectra of both the hydrogenated product and the starting material were then examined to see what effects the C-Cl bond has on the vibrational frequencies of the molecule. The versions of the molecule which had already been minimised by ChemBio3D were subjected to further geometric optimisation before the IR spectra were calcuated. The 3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation was used using 'SCAN' as opposed to the laptop because it takes a long time to run. The output file, .fchk, was opened in Gaussview to get the IR spectra, shown below. The Cl-C and C=C stretching frequencies have been tabulated and also given below. Going from the diene to the alkene the C-Cl bond becomes slightly lower in frequency, and is more rigid. This implies that the bond has become a higher in energy upon hydrogenation, but the difference is negligible. The same applies to the other C=C vibration. However, the difference between the C=C vibrations is where the clearest comparison can be drawn. The double bond which was hydrogenated has a lower frequency, and is higher in energy and more rigid than the other bond. This is because there is less orbital overlap from the Cl atom into the LUMO of the alkene, which is an anti-bonding orbital. The bond therefore shows more double bond character than the other bond, hence it is more reactive.

	C-Cl/cm-1	C=C/cm-1
Diene	771	1737, 1757
Alkene	775	1758

Module 1b: Structure and Spectroscopy

Structure based mini-project using DFT-based molecular orbital methods

Introduction

In this section a reaction reported in primary literature (Tetrahedron: Asymmetry) was investigated. This reaction gives rise to two non-isomeric products, but only the first, highlighted by the red box, was chosen.(1S,4R,5R,6S)-4-cyano-5,6-dihydroxycyclohex- 2-enyl acetate, (+)-10 has two possible distereoisomers. Computational techniques were implemented to predict the ¹³C NMR spectrum in order to predict the structure, and thus distinguish between the two isomers. The IR spectra, dihedral angles, J-coupling values and optical rotations were also investigated.

Isomer 1

Isomer 2

The compound was prepared in the following manner: "Lipase from R. miehei (50 mg) was added to a solution of (±)-4 (62 mg, 0.400 mmol) in tetrahydrofuran (5 ml) containing vinyl acetate (3 equiv). The suspension was shaken (300 rpm) at 45°C, aliquots were drawn at regular time intervals and monitored by TLC (MeOH/CH2Cl2) and gas chromatography. After 24h the reaction was quenched, the catalyst filtered off, and the filtrate evaporated to dryness in vacuum. The residue was purified by flash chromatography on silica gel (MeOH/CH2Cl2 gradient) affording compound (+)-10 (36.32 mg, 0.184 mmol, 46% yield) as an oil."

As with the previous examples the MM2 and MOPAC/PM6 minimisation was carried out and tabulated; all values are in kcalmol^-1. The results are fairly similar, which was expected as they are disteroisomers. The stretching energies are very low, suggesting that the bond lengths are quite close to what is ideal, whereas the bending energies are slightly higher, indicating the bond angles are distorted compared to the equilibrium bond angles. The torsion energies are however low, so there is little strain on the molecule. The van der Waals' forces indicate some attraction in the molecule which promotes stabilisation and the dipole-dipole energies indicate poliarity in the molecule, caused by a number of electronegative atoms in the molecule. Whilst both total energies are low, isomer 2 is marginally less than 1. Isomer 1 is however the predominant product at a 98% yield, suggesting that other factors aside thermodynamic ones are more influential in determining which product forms. This product has retention of stereochemistry, so the reaction is not S_N2 in nature (it is more likely to be S_N1 as this results in a racemic mixture).

	Stretching	Bending	Torsion	Van de Waals	Dipole-dipole	Total energy	Heat of formation
Isomer 1	0.97	6.57	-0.74	8.32	8.13	21.5	-139
Isomer 2	0.86	6.63	-0.95	8.87	6.32	18.5	-136

Predicting the ¹³C NMR spectrum of a compound

NMR allows for conformation that the expected product has formed, as it analyses the different environments the nuclei under investigation is in. It should be able to distinguish between the two disteroisomers; although it is only the angle at which the carbon causing the isomerisation has changed, the resultant environments should differ slightly. The experimentally recorded ¹³C spectrum for this compound, in ppm, is as follows:

Experimental - ¹³C NMR (CD₃OD): 171.2 (1C, CO), 125.8 (1C, C-3), 122.5 (1C, C-2), 120.9 (1C, CN), 76.4 (1C, C-6), 71.4 (1C, C-5), 70.1 (1C, C-4), 36.7 (1C, C-1), 20.9 (1C, –CH3).

Isomer 1 was drawn out and an MM2 optimisation, followed by a MOPAC/PM6 was run on it. A Gaussian input file was then created: job Type - minimise, method - DFT=mpw1pw91, basis set - 6-31G(d,p). This particular method was chosen over the B3LYP because it gives better results for the NMR properties. After being edited to read '# mpw1pw91/6-31g(d,p) opt(maxcycle=25) (...etc)' the file was sent off to SCAN for geometry optimisation. The returned file could then be prepared for NMR by changing the top line in the file to '# mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=methanol)'. The NMR for the compound was run in methanol, as opposed to the more commonly used solvent chloroform because the literature spectrum was recorded in the former. The result, which was downloaded as a Gaussian log file, was then opened in Gaussview. For the NMR spectrum the selected nucleus was obviously C, and the appropriate reference value was TMS mPW1PW91/6-31G(d,p) GIAO. From this, the individual peaks were selected to obtain the NMR values; which has scope for error because the position at which the peak was clicked on was not exact. The same procedure was then repeated with isomer 2, and the obtained values, in ppm are:

Isomer 1 - ¹³C NMR (CD₃OD): 168.2 (1C, CO), 129.0 (1C, C-3), 125.0 (1C, C-2), 115.5 (1C, CN), 71.3 (1C, C-6), 70.7 (1C, C-5), 69.9 (1C, C-4), 36.9 (1C, C-1), 25.3 (1C, –CH3).

Isomer 2 - ¹³C NMR (CD₃OD): 167.9 (1C, CO), 129.9 (1C, C-3), 122.1 (1C, C-2), 117.6 (1C, CN), 80.5 (1C, C-6), 80.3 (1C, C-5), 74.1 (1C, C-4), 41.6 (1C, C-1), 18.7 (1C, –CH3).

As none of the peaks for isomer 1 are more than 5ppm out, it can be assumed that the correct configuration was reported in the literature. For the second isomer, some of the peaks are out of range of the literature (but not by considerable amounts, ~1-9ppm) which confirms that this the experimental NMR is not of this one. For this molecule, the method is shown to be quite accurate in predicting the ¹³C NMR spectrum; the correct number of peaks has been calculated and at the correct shifts in relation to the experimental. A ¹H spectrum was not run because it needs greater precision in order to get successful results.

Predicting the ³J H-H couplings of a compound

Isomer 1

Isomer 2

Although ¹H spectra could not be computed, the ³J coupling could be calculated based on the data obtained from the NMR predictions. ChemBio3D was used to save a 3D model of each isomer as a .mol file, which was then opened in an online programme called Janocchio, which gave the coupling constants. For each isomer, the relevant hydrogens have been assigned a number to make the coupling constants clearer. The ones reported in the literature and calculated are as follows; all values are in Hz:

	H-1	H-2	H-3	H-4	H-5	H-6
Literature	dd = 7.9, 2.0	ddd = 10.0, 2.1, 2.0	ddd = 10, 2.2, 2.7	ddd = 9.7, 2.9, 2.2	t = 9.7	dd = 9.7, 8.0
Isomer 1	dd = 3.9, 1.8	ddd = 4.4, 4.1, 1.8	ddd = 4.4, 3.9, 1.5	ddd = 3.1, 3.0, 1.5	dd = 8.2, 3.1	dd = 8.2, 3.9
Isomer 2	dd = 8.4, 0.16	ddd = 8.4, 6.3, 1.7	ddd = 8.2, 6.3, 5.4	ddd = 5.4, 2.6, 2.7	dd = 8.2, 2.6	dd = 8.4, 8.2

Not only are experimental and computational values are extremely different, in one case a double doublet was obtained when the experimental NMR reports a triplet. This suggests that the bond angles for both optimised molecules are wrong, Janocchio is not calculating the coupling constants correctly or, much less likely the J-couplings reported are incorrect (but the chance of this is minimal). Another way of obtaining J-coupling constants would be to use Gaussian, which would allow us to check the source of the error. This is a quantum mechanical approach, but since it has high accuracy the procedure takes a very long time to run. Both sets of isomers also have very different coupling constants when compared to one another.

Predicting the IR spectrum of a compound

IR spectrum

The IR spectrum is a useful way of checking what functional groups are present in the molecule, and whether or not this matches up to what was expected. It is a quick analytical method, but it cannot alone predict the structure of a molecule. In the literature an IR spectrum was not recorded of this compound, however one has been computed. Both isomers will show the same IR because they have the same functional groups, therefore only one was run.

	C=O/cm-1	C=C/cm-1	C=N/cm-1	O-H/cm-1
Isomer	1854	1745	2357	3814

These stretches are in line with what would be expected if an IR spectrum were to be recorded because the functional groups are vibrating in the correct regions, and there are not any vibrations present that were unexpected. The This shows that the programme seems to be computing this molecule with good accuracy. With no IR data present for this compound, this cannot be confirmed.

Predicting the optical rotation (OR) and the electronic circular dichroism (CD/UV-Visible) spectrum of a compound

Optical density investigates how a plane of polarized light interacts with a molecule, which is especially important with chiral molecules. This light will rotate in an equal and opposite direction through each of the disteroisomers. The nature of this calculation means that it is highly sensitive to slight changes in molecules, therefore a full quantum mechanical approach has to be implemented over a more simpler one that could be used for the other spectra. The molecule under investigation qualifies for this calculation because its optical rotation has been reported to be >100, which is essential because the method is unreliable if the value is below this.

To run the optical rotation, the following line had to be inserted in the top line of the optimized geometry file before submission '# cam-b3lyp/ 6-311G(d,p) polar(optrot) scrf(IEFPCM,solvent=chloroform) CPHF=RdFreq'. The Cambridge method was chosen because it is better than the normal one in predicting the chiro-optical properties of a molecule. For the asymmetric molecule, it calculates the [alpha]D optical rotation components. The incident wavelength chosen is 589nm because this is the sodium D line. In order to make a better comparison, both isomers were run because they should give equal and opposite rotations. The method is very sensitive to changes in a molecule, but it is only reliable when [Alpha]D > 100°. For isomer 1 [Alpha] ( 5890.0 A) = +246°, but for isomer 2, [Alpha] ( 5890.0 A) = -55.7°. Both are different to the literature value of +102°, suggesting that either the optimised geometry of both isomers is incorrect or there is an error in the calculations which gave rise to these values.

The circular dichroism spectrum looks at the how left and right circularly polarized light is absorbed; it is similar to a UV spectrum but it uses chiral light instead. It is used on optically active chiral molecules because whilst the intensities should expected to be the same for each electron transition, the signs should be opposite, such that the spectra are a mirror image of each other. This calculation is much more sensitive to changes in the structure of the molecule, so there is a lot more scope for error. For this molecule, the first 20 electronic singlet excitations were included. The top line of the file was changed to '# cam-b3lyp/6-311G(d,p) td(NStates=20) scrf(IEFPCM,solvent=chloroform)'. Whilst this technique was run for each isomer, it was not possible to draw a spectrum on Gaussview for either; the procedure was repeated but the same problem still occurred.

Conclusion

As shown by the numerous examples, computational techniques have their benefits but also limitations in predicting the structure and reactivity of a variety of compounds. Not being able to handle aromatic, hyperconjugated, etc compounds is a heavy limitation of the MM2 model, however its prediction when these functionalities are not present is very accurate. Other methods have shown similar successes. It can therefore be concluded that computational techniques are extremely useful in not only providing an idea of what product has been obtained from a reaction, or the structure and reactivity of a certain molecule, but in the mini-project and other examples it shows the ability to distinguish between two isomeric products. Although not free of errors, done correctly it has the potential to confirm data obtained from an experiment or check that the correct product has been predicted and synthesised.

As a side note, out of all the techniques investigated in the mini-project, the ¹³C NMR was by far the most useful - it had the highest accuracy and NMR is one of the most useful techniques in determining the structure of the molecule. The IR spectrum, whilst less important, allowed for a quick check of the functional groups in the molecule. The other 3 techniques - J-coupling, optical rotation and electronic circular dichroism were much less useful because of either the errors associated in the programmes, or the structure itself, whether this be the molecule itself or the way it was drawn and optimised.