Jump to content

Rep:Mod:rs7913TSmmk

From ChemWiki

Introduction

Non-linear chemical systems undergoing a reaction may be displaced in 3N-6 degrees of freedom, where N is the number of atoms in the system. This number corresponds to the number of vibrational modes the system has; for a linear molecule this number would be 3N-5. A 2-dimensional potential energy surface can be used to display how potential energy varies with any two of these degrees of freedom. Often, displacing a reactant along different degrees of freedom can lead to the formation of different products, as can be seen in Figure 1.

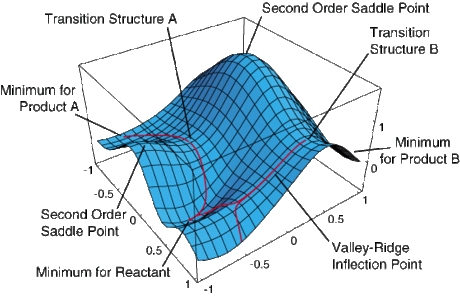
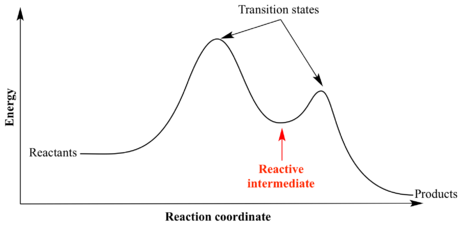
Figure 1: A typical potential energy surface.

A transition state is a maximum in potential energy along one of these reaction coordinates, and hence a stationary point (first derivative dE/dr = 0) with a negative second derivative along this reaction coordinate (d2E/dr2 = -ve). Chemical systems always seek to minimise potential energy, therefore they will tend towards minimums in potential energy, hence transition states have a fleeting existence and cannot be characterised. Furthermore, chemical reactions do indeed proceed via the lowest energy route possible, so a transition state is a maximum along a minimum energy path from reactants to products. This means that a transition state is a saddle point on a potential energy surface, as can be seen in Figure 2, and that the second derivative along all other reaction coordinates is negative. Minimums in such potential energy surfaces are stationary points with a positive second derivative along all reaction coordinates, and correspond to reactants, products or intermediates in a chemical reaction. Using a simple harmonic approximation for molecular vibrations (as the chemical system is displaced along a particular reaction coordinate), the second derivative d2E/dr2 is equal to the force constant, k, for the vibration.

Figure 2: Energy profile for a reaction that proceeds via an intermediate.


Computational Optimisation Methods

Programs like Gaussian use the LCAO approach to approximate molecular orbitals (MOs) from an atomic orbital (AO) basis set, and there are an infinite number of AOs that could be included. The larger the basis set, the better the approximation, however the calculation will take longer and require more computing power. The PM6 and B3LYP (d) optimisation methods were used in this lab. The PM6 method is semi-empirical; it uses empirical data in place of solving some integrals in the Hamiltonian matrix when carrying out LCAO as well as using density functional theory (DFT), Haretree-Fock (HF) and molecular mechanics methods. DFT solves the Hamiltonian matrix with respect to the electron density of the system, whereas the HF method solves the Hamiltonian matrix with respect to the individual electronic positions. The B3LYP method is a hybrid method that uses DFT and HF methods to solve the Hamiltonian matrix a priori. It is more accurate than the PM6 method, which does itself yield reasonable results, however the calculations do take a relatively long time. For this reason, in the lab the PM6 method was used to generate initial geometries, which were then optimised using the B3LYP method in Exercise 2. In Exercises 1 and 3, the PM6 optimisation was sufficient to carry out the required analysis.

The Reaction of Butadiene with Ethylene

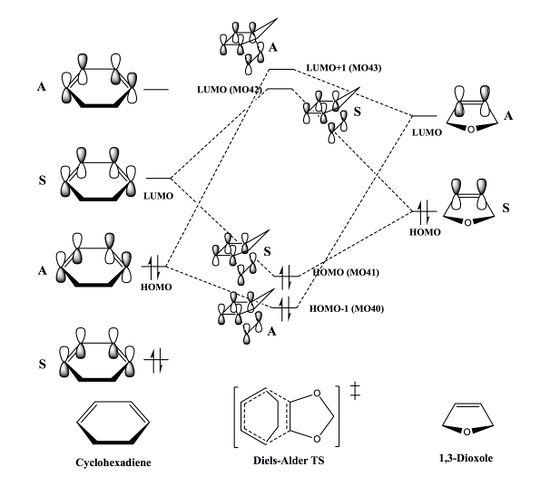
The reaction of butadiene with ethylene is known as a Diels-Alder reaction, and is also often referred to as a [4+2] cycloaddition. It is a classed as a pericyclic reaction, being concerted and proceeding via a (6-membered) cyclic transition state. Atomic orbitals of the same symmetry as well as similar energy can be considered to interact to give the MOs in the product, with symmetry conserved. This is confirmed by inspection of the MOs of the transition state (Figure 4), and considering which atomic orbitals have been combined (LCAO) to create these MOs. Only orbitals of the same symmetry interact since only this combination gives rise to non-zero overlap. This is confirmed by examination of the transition state MOs 16-19, each of which are a combination of butadiene and ethylene MOs of the same symmetry. Empirically derived Woodward-Hofmann rules are often used to predict whether thermal pericyclic reactions will proceed and the reason why these rules hold is based around this idea of orbital symmetry. Since this reaction is a [π4s+π2s] cycloaddition (proceeds via a suprafacial-suprafacial interaction between a conjugated 4π electron system (the diene) and a 2π electron system (the dienophile)), it is thermally allowed according to the Woodward-Hofmann rules.[1]

Table 1: Symmetry of orbital interactions and the resulting orbital overlap.
Interaction Orbital Overlap Integral
symmetric-symmetric non-zero
antisymmetric-antisymmetric non-zero
symmetric-antisymmetric zero
Butadiene LUMO
Ethylene LUMO
Butadiene HOMO
Ethylene HOMO

Figure 3: The frontier MOs of butadiene and ethylene, optimised at the PM6 level.

MO16 (HOMO-1)
MO18 (LUMO)
MO17 (HOMO)
MO19 (HOMO+1)

Figure 4: The HOMO-1, HOMO, LUMO and LUMO+1 of the transition state.


Figure 5: Molecular orbital diagram for the formation of the butadiene/ethylene transition state.

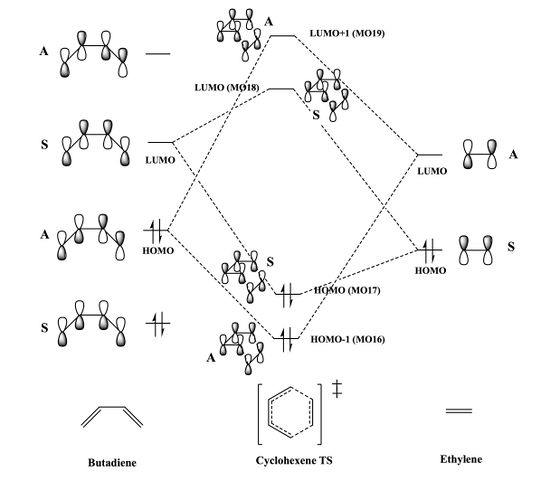
Computed energies of the butadiene and ethene frontier MOs confirm that this is a normal electron demand reaction, where the HOMO of the diene and LUMO of the dienophile are closest in energy and interact most strongly[2][3], giving rise to MOs 16 and 19. This is reflected in the MO diagram for the formation of the butadiene/ethylene transition state (Figure 5). It is conventional for the diene to be the more electron rich component in the reaction. In contrast, inverse electron demand occurs when the HOMO of the dienophile and LUMO of the diene are closest in energy and give rise to the strongest interaction. Inverse electron demand often takes place when the diene bears electron-withdrawing substituent(s) and/or the dienophile bears electron-donating substituent(s).

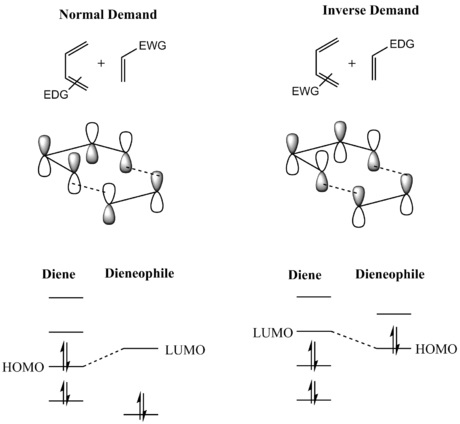
Figure 6: Frontier molecular orbitals and electron demand in Diels-Alder reactions.

However, the frontier molecular orbitals - the HOMO-1 and HOMO, and LUMO and LUMO+1 - of the transition state are very close in energy, which indicates that this reaction could be between a normal and inverse electron demand reaction. This is reasonable, since neither the dienophile is not bearing any electron withdrawing substituents, and the diene does not bear any electron donating substituents. Calculations were carried out using the PM6 optimisation method; one could gain a more accurate insight into the electron demand of this reaction by repeating calculations using a more accurate method, for example B3LYP.

C-C Bond Lengths of the Reactants and Product

Table 2: C-C bond lengths of the reactants, transition state, and product.
Distance Reactants Transition State Product
C1-C2 1.335 1.380 1.501
C2-C3 1.468 1.411 1.337
C3-C4 1.335 1.380 1.501
C4-C5 - 2.114 1.537
C5-C6 1.327 1.382 1.535
C6-C1 - 2.115 1.537

Van der Waals radius of the C atom: 1.70 Å

sp2 C=C bond length: 1.33 Å

sp3 C-C bond length: 1.54 Å

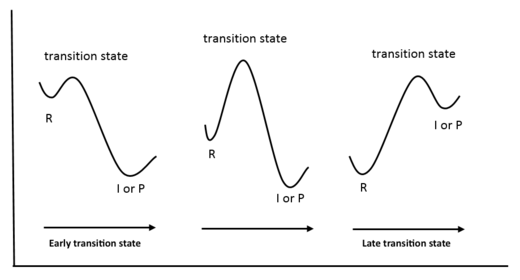
In the transition state, atoms C4 and C5, and C6 and C1, lie 2.114 Å apart. This is consistent with the formation of C-C single bonds, since the distance more is in between double the Van der Waals radius of the C atom (3.40 Å) and the sp3 C-C bond length (1.54 Å). By analysing the IRC calculated for the reaction (at the PM6 level), it was found that these bond lengths decrease fairly linearly from the transition state separation (2.114 Å) to a distance of 1.537 Å, which is consistent with an sp3 C-C bond. The distances C1-C2 and C3-C4 both increase from around 1.335 Å in the reactant (butadiene) to 1.501 Å in the product, and in the transition state this distance is 1.380 Å - in between the sp2 C=C and sp3 C-C bond lengths. This is consistent with the C=C double bonds in butadiene becoming C-C single bonds in cyclohexene. The distance between atoms C2 and C3 decreases from 1.448 Å in the reactant (butadiene) to 1.337 Å in the product, and is 1.411 Å in the transition state - in between sp3 C-C and sp2 C=C bond lengths. This is consistent with the C-C bond in butadiene becoming the C=C double bond in cyclohexene. The distance C5-C6 increases from 1.327 Å in the reactant (ethylene) to 1.535 Å in the product, and is 1.382 Å in the transition state - in between sp2 C=C and sp3 C-C bond lengths. This is consistent with the C=C double bond in ethylene becoming a C-C single bond in cyclohexene. It can be seen that the C-C distances in the transition state are considerably closer to those in the reactants than the product. This indicates that this reaction has an early transition state according to the Hammond Postulate[4], since the interconversion between the reactants and transition state involves a smaller reorganisation of molecular structure than that for the interconversion between the transition state and product, hence the reactants and transition state lie closer in energy. Of course, the fact that this reaction is exothermic confirms that it has an early transition state. This is illustrated in Figure 7.

Figure 7: Reaction energy profiles illustrating early and late transition states.

Frequency Analysis of the Transition State

As mentioned in the introduction, a transition state has a negative second derivative with respect to energy (d2E/dr2) along one reaction coordinate - that corresponds to the reaction path - but a positive second derivative with respect to all other degrees of freedom. It was also noted that a minimum in a potential energy surface will of course have a positive second derivative with respect to all reaction coordinates. Gaussian does use a simple harmonic approximation for molecular vibrations (as the chemical system is displaced along a particular reaction coordinate), hence the second derivative d2E/dr2 is equal to the force constant, k, for the vibration, as noted earlier. Hence, a frequency analysis can be carried out to easily confirm whether a computed structure corresponds to a minimum in the potential energy surface (reactant, product or intermediate) or a transition state. For simple harmonic motion, the frequency of a vibration, ω, is equal to the square root of the force constant, k, divided by the reduced mass of the system, m:

ω = √(k/m)

Therefore, a minimum will have only positive frequencies for displacements along all reaction coordinates, and a transition state will have only one imaginary frequency, along the reaction coordinate that corresponds to the reaction path at the transition state. This imaginary frequency is represented as a negative number in Gaussian.

The vibration shown in Figure 8 is at '-948.25' cm-1, and corresponds to the reaction path at the transition state. This symmetric vibration clearly displays that the formation of the two new C-C bonds is synchronous, and is the only negative vibration at this transition state.

Figure 8: Vibration at '-948.25' cm-1.

The lowest energy vibration (Figure 9) is at 145.12 cm-1, and it can clearly be seen that this does not correspond to the Diels-Alder reaction discussed.

Figure 9: Vibration at 145.12 cm-1.

The Reaction of Cyclohexadiene and 1,3-Dioxole

The two oxygen atoms on 1,3-dioxole are electron-withdrawing by induction, however they are overall strongly electron-donating due to resonance, i.e. π-conjugation involving the C=C π* orbital and the lone pairs on the oxygen atoms in the same plane. This results in destabilisation of frontier MOs of the dienophile in this Diels-Alder reaction, resulting in inverse electron demand as explained in the previous section. Inverse electron demand is confirmed by the fact that the HOMO of the dienophile (1,3-dioxole) and LUMO of the diene (cyclohexadiene) are closer in energy than the HOMO of the diene and the LUMO of the dienophile. This is illustrated in the MO diagram (Figure 13) for the cycloaddition.

The geometries involved in this cycloaddition were first located at the PM6 level, however this less accurate computational method resulted in negative reaction barriers being calculated, which were of course inaccurate. Therefore, all geometries were subsequently optimised at the B3LYP/6-31G(d) level, and the reaction barrier and energy for both the endo and exo reactions were calculated as follows.

Cyclohexadiene LUMO
1,3-Dioxole LUMO
Cyclohexadiene HOMO
1,3-Dioxole HOMO

Figure 10: The frontier MOs of cyclohexadiene and 1,3-dioxole, optimised at the B3LYP level.

MO40 (HOMO-1)
MO42 (LUMO)
MO41 (HOMO)
MO43 (HOMO+1)

Figure 11: The HOMO-1, HOMO, LUMO and LUMO+1 of the endo transition state, optimised at the B3LYP level.

MO40 (HOMO-1)
MO42 (LUMO)
MO41 (HOMO)
MO43 (HOMO+1)

Figure 12: The HOMO-1, HOMO, LUMO and LUMO+1 of the exo transition state, optimised at the B3LYP level.

Figure 13: Molecular orbital diagram for the formation of the cyclohexadiene/1,3-dioxole transition state.
Table 3: Free energies of the reactants, transition states and products.
Species Sum of electronic and thermal Free Energies (Hartree/Particle) Sum of electronic and thermal Free Energies (kJ/mol)
Cyclohexadiene -233.324375 -612593.19
1,3-Dioxole -267.068132 -701187.43
Endo TS -500.332146 -1313622.15
Endo Product -500.418691 -1313849.37
Exo TS -500.329164 -1313614.32
Exo Product -500.417322 -1313845.78
Table 4: Calculated reaction barriers and energies for the endo and exo reactions.
Endo Reaction Barrier (kJ/mol) Endo Reaction Energy Exo Reaction Barrier Exo Reaction Energy
-1313622.15 - (-612593.19 - 701187.43) = 158.47 -1313849.37 - (-612593.19 - 701187.43) = -68.75 -1313614.32 - (-612593.19 - 701187.43) = 166.30 -1313845.78 - (-612593.19 - 701187.43) = -65.16

The endo product is both kinetically and thermodynamically favoured over the exo product, since the endo reaction barrier is lower and the reaction energy is more negative. In the LUMO of the endo transition state (Figure 11), a favourable secondary orbital interaction can be seen between the oxygen p-orbitals (lone pairs) on 1,3-dioxole and the cyclohexadiene π-system, which stabilises this transition state. No such interaction can be seen in the exo transition state (Figure 12), since the oxygens are pointing away from the cyclohexadiene π-system. Although the endo product is more sterically hindered than the exo product, it's stability can once again be attributed to a similar orbital interaction between the oxygen p-orbitals (lone pairs) and the C=C double bond (π-MO) in the cyclohexane ring. This interaction can be seen in the HOMO of the endo product, however in HOMO of the exo product, once again because the oxygens are pointing away from the C=C double bond, this interaction cannot be seen.

Xylylene-SO2 Cycloaddition

The PM6 method was used to optimise the structures involved in this reaction, and IRCs were calculated at this level.

Figure 14: IRC visualisation for the Endo Diels-Alder reaction.
Figure 15: IRC visualisation for the Exo Diels-Alder reaction.
Figure 16: IRC visualisation for the Cheleotropic reaction.

In the IRCs calculated (Figures 14,15,16), one can see that the 6-membered ring regains aromaticity, releasing a considerable amount of energy. This makes xylylene highly thermodynamically unstable, and the numerous decomposition pathways possible mean xylylene is kinetically unstable as well. Aromaticity seems to be regained slightly before the formation of the heterocycle - this is most apparent in the cheletropic reaction - and is testament to the fact that a substantial amount of energy is released on regaining aromaticity.

As for the reaction between cyclohexadiene and 1,3-dioxole, the reaction barrier and energy for each reaction was calculated. However, these calculations were carried out using thermochemical data from optimisations at the PM6 level. The results seem reasonable, so the structures involved were not further optimised using a more precise method such as B3LYP.

Table 5: Free energies of the reactants, transition states and products.
Species Sum of electronic and thermal Free Energies (Hartree/Particle) Sum of electronic and thermal Free Energies (kJ/mol)
O-Xylylene 0.178061 467.499
SO2 -0.119269 -313.141
Endo TS 0.090559 237.763
Endo Product 0.021704 56.984
Exo TS 0.092079 241.753
Exo Product 0.021453 56.325
Cheletropic TS 0.099062 260.087
Cheletropic Product 0.000000 0.000
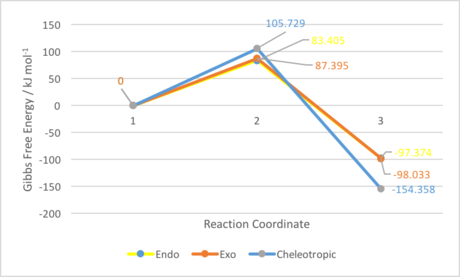
Table 6: Calculated reaction barriers and energies for the endo, exo and cheletropic reactions.
Endo Reaction Barrier (kJ/mol) Endo Reaction Energy (kJ/mol) Exo Reaction Barrier (kJ/mol) Exo Reaction Energy (kJ/mol) Cheletropic Reaction Barrier (kJ/mol) Cheletropic Reaction Energy (kJ/mol)
237.763 - (467.499 - 313.141) = 83.405 56.984 - (467.499 - 313.141) = -97.374 241.753 - (467.499 - 313.141) = 87.395 56.325 - (467.499 - 313.141) = -98.033 260.087 - (467.499 - 313.141) = 105.729 0.000 - (467.499 - 313.141) = -154.358

As can be seen, the endo product is favoured kinetically over the exo product, which is in turn favoured kinetically over the cheletropic product by a considerable amount. This could be attributed to the fact that a more hindered 5-membered ring is forming in the cheletropic transition state, compared to the 6-membered ring that is being formed in the Diels-Alder transition states. Furthermore, in both Diels-Alder transition states there is a considerably favourable orbital interaction between the oxygen p-orbital (lone pair) that will be incorporated into the ring and the diene in the same plane; no such interaction can be seen in the cheletropic transition state. The fact that the endo reaction barrier is lower than that for the exo reaction could be attributed to a favourable secondary orbital interaction between the diene and the oxygen pointing towards the ring in the endo TS but away in the exo TS, however this is not a strong interaction, and is not clear-cut in the MOs computed.

However, the cheletropic product is thermodynamically favoured by a relatively large amount. This can be attributed to the fact that the sulfur-oxygen double bond (in the cheletropic product) is considerably stronger than a sulfur-oxygen and carbon-oxygen single bond (in the Diels-Alder products). Therefore, carrying out the reaction under equilibrating, thermodynamic conditions will result in formation of the cheletropic product. The exo product is thermodynamically favoured over the endo product by a small amount. This could be attributed to slightly less steric hindrance involving the terminal oxygen atom pointing away from the ring in the exo product, compared to towards the ring in the endo product. However, this effect will not be great since neither the exo nor endo products are greatly hindered, since they are both planar bicyclic systems. These results must be treated with some caution since the less accurate PM6 method was used for the optimisations; once again, a more accurate method such as B3LYP could be used to optimise the structures and gain more reliable results for the energetics of this reaction.

Figure 17: Reaction profile displaying the endo, exo and cheletropic paths of the Xylylene-SO2 cycloaddition.

Conclusion

Computational optimisations were carried out to study three cycloaddition reactions; that between butadiene and ethylene, cyclohexadiene and 1,3-dioxole, and xylylene and SO2. This allowed for rationalisation of the thermodynamic and kinetic profiles of these reactions, however thermochemical results were not always accurate using the semi-empirical PM6 method - in these cases the structures that were of concern were further optimised using the more accurate B3LYP method, which yielded plausible results. This was necessary to get reasonable results for the reaction of cyclohexadiene and 1,3-dioxole.

References

  1. ↑ R. B. Woodward and R. Hofmann, J. Am. Chem. Soc., 1965, 87, 395-397. 
  2. ↑ L. Salem, J. Am. Chem. Soc., 1968, 90, 543-553.
  3. ↑ G. Klopman, J. Am. Chem. Soc., 1968, 90, 223.
  4. ↑ G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334-338.

Appendix 1: Log Files For Calculations Carried Out

The Reaction of Butadiene with Ethylene

Calculation PM6
Butadiene RS7913_BUTADIENE.LOG
Ethylene RS7913_ETHYLENE.LOG
Transition State RS7913_BUTADIENE_ETHYLENE TS.LOG
IRC RS7913_BUTADIENE_ETHYLENE_IRC.LOG
Cyclohexene RS7913_CYCLOHEXENE_PRODUCT.LOG

The Reaction of Cyclohexadiene and 1,3-Dioxole

Calculation PM6 B3LYP
Cyclohexadiene - Jmol included
1,3-Dioxole - Jmol included
Endo Transition State - Jmol included
Endo Product - RS7913_ENDO_PRODUCT_B3LYP.log
Endo IRC RS7913_ENDO_TS_IRC.LOG -
Exo Transition State - Jmol included
Exo Product - RS7913_EXO_PRODUCT_B3LYP.log
Exo IRC RS7913_EXO_TS_IRC.LOG -

Xylylene-SO2 Cycloaddition

Calculation PM6
Xylylene RS7913_Xylylene_PM6.log
SO2 RS7913_SO2_PM6.log
Endo Transition State RS7913_Endo_TS_PM6.log
Endo Product RS7913_Endo_product_PM6.log
Endo IRC RS7913_Endo_IRC.log
Exo Transition State RS7913_Exo_TS_PM6.log
Exo Product RS7913_Exo_Product_PM6.log
Exo IRC RS7913_Exo_IRC.log
Cheletropic Transition State RS7913_CHELETROPIC_TS.LOG
Cheletropic Product RS7913_Cheletropic_Product_PM6.log
Cheletropic IRC RS7913_Cheletropic_IRC.log
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:rs7913TSmmk&oldid=820682"