Rep:Mod:rs6112inorgcomplab

Week 1

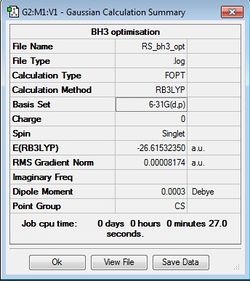
BH₃ Optimisation

B3LYP/3-21G

Optimisation log file here.

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000010 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000045 0.000060 YES RMS Displacement 0.000013 0.000040 YES	Optimised Molecule

B3LYP/6-31G(d,p)

A better basis set was used to get a more accurate optimisation of BH₃. It was observed that the energy calculated was different from that calculated using the 3-21G basis set.

Optimisation log file here.

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000653 0.001800 YES RMS Displacement 0.000415 0.001200 YES	Optimised Molecule

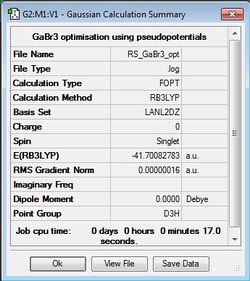
GaBr₃ Optimisation

B3LYP/LANL2DZ

Optimisation file: DOI:10042/31141 .

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES	Optimised Molecule

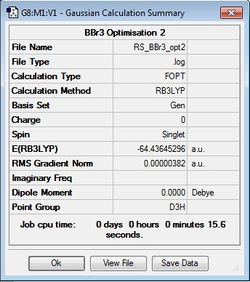
BBr₃ Optimisation

B3LYP/6-31G(d,p)LANL2DZ

Optimisation file: DOI:10042/31148 .

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES	Optimised Molecule

Geometry Information

The computed bond lengths and bond angles are shown in the table below.

Geometry Data

	BH3	BBr3	GaBr3
r(E-X) Å	1.19	1.93	2.35
θ(X-E-X) degrees(º)	120.0	120.0	120.0

Analysis of Results

Changing the central atom does not affect the geometry of the molecule since the molecule remains trigonal planar with the same symmetry, D_3H. Hence the bond angles for all three compounds are 120.0º, as expected for a trigonal planar compound where the three ligands want to be as far apart as possible to minimise electronic repulsion. However, changing the central changes the bond length between the central atom and the ligand. The bond length increases as the atoms are changed to larger atoms. Bond length differences could also be due to differences in bond order and bond strength.

Comparing between BH₃ and BBr₃, as the ligand is changed from H to Br, the E-X bond length increases from 1.19 Å to 1.93 Å. The increase in bond length is mainly due to the atomic radius of Br being larger than that of H. H and Br are similar in that they both form single bonds with the central boron atom. However H only has one valence electron while Br has seven valence electrons and has more diffuse orbitals. Also for Br, its filled p orbitals can overlap with the electron cloud of the central atom, allowing it to donate some of the electron density back to the central atom. Hence some degree of backbonding can occur with the Br ligands but not for H ligands as they are too small and cannot donate electron density back to the central atoms. This makes the B-Br bond stronger than the B-H, hence the bond length does not increase a lot from B-H to B-Br due to a higher bond strength.

Comparing between BBr₃ and GaBr₃, as the central atom is changed from B to Ga, the E-X bond length increases from 1.93 Å to 2.35 Å. This is due to the larger atomic radius of Ga compared to B since it is further down the group. The bond length does not increase as much since Ga is in the same row as Br and there is better overlap between the similarly sized orbitals of Ga and Br, as compared to between the orbitals of B and Br. The Ga-Br bond is hence also stronger than the B-Br bond and would have a higher bond dissociation energy.

B and Ga are both Group III elements, hence they both have only three valence electrons and form electron-deficient EX₃ compounds. Ga is a larger atom than B hence its orbitals are more diffuse and there is a fair amount of shielding by the inner electron shells from the nuclear charge.

Bonding

Bonds are interactions between atoms that hold them together due to the attractive electrostatic forces present between the atoms, lowering the overall energy of the molecule. It is also visualised as the overlap of individual atomic orbitals to form molecular orbitals. There are different kinds of bonds: strong bonds such as covalent and ionic and weaker bonds such as hydrogen bonds. Stronger bonds have a higher force constant and have higher energy. For covalent bonds, the higher the bond order, the greater is the strength of the bond. For example, N ≡ N bond is a strong bond with a bond order of 3 and bond dissociation energy of 962 kJ/mol. A C-C bond is an example of a medium bond with a bond order of 2 and bond energy of 368 kJ/mol. On the other hand, I — I is a weak bond with a bond energy of 151 kJ/mol due to the poorer overlap between the large diffuse orbitals of the iodine atoms. A very weak bond such as a hydrogen bond would have a bond energy of 20 kJ/mol .

For some structures where expected bonds are not drawn in by GaussView, it does not mean that there is no bond present. It means that the distance between the two atoms exceed the average bond length. GaussView draws bonds based on distance calculations and comparisons to the average bond length for those atoms, so it does not draw the bonds that exceed a certain distance value. There can be attractive forces between the atoms even if their distances are further apart than the threshold, hence there can be still molecular interactions between the atoms.

Frequency Analysis

BH₃:B3LYP/6-31G(d,p)

Frequency file: here

Summary Data	Low Modes
	Low frequencies --- -10.1940 -10.1821 -3.1776 0.0008 0.0579 0.4920 Low frequencies --- 1162.9850 1213.1461 1213.1463

Vibrational spectrum for BH₃

Frequency (cm-1)	Intensity	IR active?	Type	Symmetry
1164	93	Yes	Bend	A2"
1213	14	Very slight	Bend	E'
1213	14	Very slight	Bend	E'
2583	0	No	Stretch	A1'
2716	126	Yes	Stretch	E'
2716	126	Yes	Stretch	E'

|

There are only three peaks observed in the IR spectrum at 2716, 1213 and 1164 (cm^-1) because one of vibrations is IR inactive, while the two of the peaks are due to two degenerate sets of vibrations. Vibrations are only IR active if they result in a change in dipole moment of the molecule. The vibration at 2583cm^-1 is an symmetric stretch with the three hydrogen atoms moving away from the central atom at the same time, hence there is no change in dipole moment and no IR peak observed. The peaks at 1213cm^-1 and 2716cm^-1 due to two sets of degenerate vibrations, which are bending and asymmetric stretching respectively. These vibrations are IR active as they cause a change in the dipole moment of the molecule.

GaBr₃:B3LYP/6-31G(d,p)

Frequency file: DOI:10042/31190

Summary Data	Low Modes
	Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982

Vibrational spectrum for GaBr₃

Frequency (cm-1)	Intensity	IR active?	Type	Symmetry
76	3	Very slight	Bend	E'
76	3	Very slight	Bend	E'
100	9	Very slight	Bend	A2"
197	0	No	Stretch	A1'
316	57	Yes	Stretch	E'
316	57	Yes	Bend	E'

|

Analysis of Results

The frequency of a vibration is proportional to the square root of the ratio of the force constant to the reduced mass as shown in the equation below.

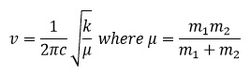
For Ga-Br the reduced mass is a lot larger than that of B-H, hence the frequencies of the vibrations are at a lower range. The difference in frequencies also indicate that the force constants for the B-H and Ga-Br bonds are different. The stronger the bond, the larger the force constant, the higher the frequency of vibration.

Comparison of A2" umbrella motion

	BH3	GaBr3
Image
Frequency (cm-1)	1164	100
Intensity	93	9

For the A2" umbrella motion, the frequency of the vibration is 1164cm^-1 with an intensity of 93 for BH₃, while it is 100cm^-1 with an intensity of 9 for GaBr₃. The nature of the vibration has changed because for BH₃, the three hydrogen atoms can be seen to be moving back and forth and the boron atom appears to be stationary, while for GaBr₃, the three Br atoms appear to be stationary as the central Ga atom moves back and forth. This could be because the Br atoms are heavier than the H atoms, hence they do not appear to move as much as the H atoms do. The frequency and intensity of the vibration is hence much lower for GaBr₃ compared to BH₃.

The same method and basis set must be used for the optimisation and frequency analysis calculations to ensure that the calculations are being carried out with the same approximations and on exactly the same molecule with the optimised geometry. The same method must be used to ensure that the operator for the Schrodinger equation is the same, and the same basis set should be used to ensure that the wavefunctions used for the calculations are the same. A simpler basis set is less accurate; for example, a calculation done using the 3-21G basis set gives less accurate result compared to that being done using the 6-31G set. The same basis set should be used for optimisation and frequency analysis to ensure that the results are useful. The purpose of carrying out a frequency analysis is to find the second derivative of the function to determine if the stationary point found is indeed a minimum point, instead of a maximum point where the first derivative is also zero. The frequencies calculated should be all positive showing that the minimum energy has been found from the optimisation. However if negative frequencies are shown in the output, it could mean that a transition state was found or that optimisation was unsuccessful. The six low frequencies represent the translational and rotational frequencies, and they should be close to zero and within the range (+/- 15 cm^-1), if not the optimisation should be repeated with a tighter convergence criteria.

BH₃ MO analysis

MO diagram for BH₃

There are no significant differences between the real and LCAO MOs. The phase distribution in the real MOs are as shown in the LCAO MOs, and the nodes are present as predicted in the LCAO MOs. It is difficult to estimate the energy levels and relative ordering of the levels in LCAO MOs as accurately as in the real MOs, but the LCAO approach is useful for understanding the general shape and interactions within the MOs. However, in the real MOs it is observed that the distinction between the orbitals are not as distinct as in the LCAO MOs. This shows that the electrons are not as localised as predicted in the LCAO MOs. It shows that MO theory is a generally good way of predicting the real MOs and hence useful in bonding analysis, though it is necessary to take note that in real MOs the electrons are more delocalised over the whole molecule.

NH₃ (Ammonia)

B3LYP/6-31G(d,p)

Optimisation of the NH₃ molecule was carried out using the B3LYP method and 6-31G(d,p) basis set.

Optimisation log file : DOI:10042/31397

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000008 0.000040 YES	Optimised Molecule

Frequency Analysis

Frequency file: DOI:10042/31399 .

Summary Data	Low Modes
	Low frequencies --- -0.0138 -0.0026 -0.0009 7.0783 8.0932 8.0937 Low frequencies --- 1089.3840 1693.9368 1693.9368

Population Analysis

Population Analysis file: here

Charge distribution

Using the NBO analysis, the charges on the different atoms can be visualised as shown in the image below. Nitrogen is highly electronegative compared to hydrogen, hence it bears a negative charge and draws electron density to itself. Each hydrogen atom then bears a positive charge of +0.375.

Charge Distribution	Specific NBO Charges
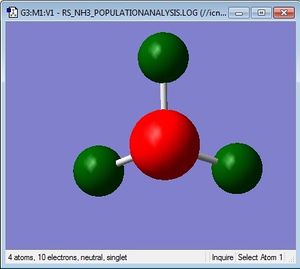
Charge Limits: -1.125 to 1.125	N: -1.125 H: 0.375

Ammonia-Borane

B3LYP/6-31G(d,p)

Optimisation log file here.

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000139 0.000450 YES RMS Force 0.000063 0.000300 YES Maximum Displacement 0.000771 0.001800 YES RMS Displacement 0.000338 0.001200 YES	Optimised Molecule

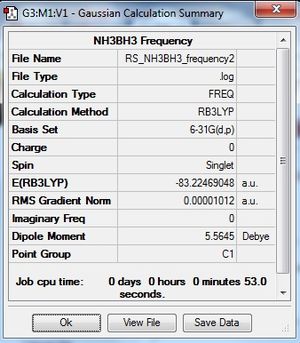
The bond angle for H-B-H was found to be 114°, and found to be 108° for H-N-H. The H-N-H bond angle is close to the bond angle expected for a sp³ hybridised nitrogen atom. The H-B-H angle is distorted from the 120° in a trigonal planar structure to 114° in this structure, as the molecule bends to reduce the incoming electronic repulsion from the NH₃ molecule.

Frequency Analysis

Frequency file: here

Summary Data	Low Modes
	Low frequencies --- -9.4461 -0.0009 -0.0008 0.0010 16.2529 20.7469 Low frequencies --- 263.8367 633.1258 638.9460

The low frequencies were found to be out of the acceptable range. Hence the optimisation of the molecule was rerun with a tighter convergence criteria to give a more accurate result and frequency analysis was done on the reoptimised molecule to give low frequencies with the range.

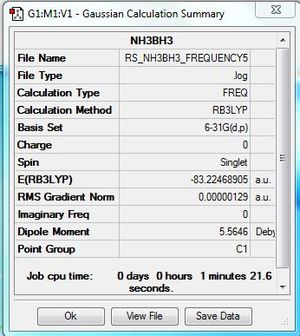
2nd Optimisation log file DOI:10042/31393 . 2nd Frequency file DOI:10042/31392 .

Summary Data	Low Modes
	Low frequencies --- -5.9230 -0.4126 -0.0009 0.0008 0.0013 2.1250 Low frequencies --- 263.4101 632.9573 638.4387

The molecule was successfully optimised using the 6-31G basis set.

The energies of the molecules optimised using the same basis set and method were used to calculate the dissociation energy of the N-B bond.

E(NH₃)= -56.5577687 au

E(BH₃)= -26.6153235 au

E(NH3BH₃)= -83.2246905 au

ΔE=E(NH₃BH₃)-[E(NH₃)+E(BH₃)]= -0.0515983 au = - 135.79 kJ/mol

NH₃ and BH₃ are joined by a dative bond, with N donating its lone pair of electron into the empty orbital of the electron deficient B. The bond energy calculated is quite low, and similar to that of a weak I-I bond, so it shows that the B-N bond is weak. This is as expected as a dative bond is not strong and does not have a high bond order.

Aromaticity Mini Project

Overview

In this project, the structure of benzene was optimised and its MOs were computed and analysed. They were then used as a basis for comparison with its isolectronic analogues, namely boratabenzene, pyridinium and borazine.

Benzene Optimisation & MO Analysis

B3LYP/6-31G(d,p)

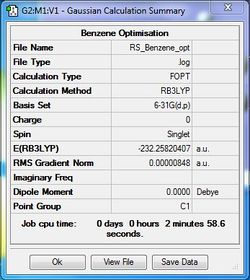
Benzene was optimised using the B3LYP as method and 6-31G as the basis set.

Optimisation file: DOI:10042/31262 . The details of the successfully optimised molecule are shown in the table below.

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000013 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES	Optimised Molecule

Frequency Analysis

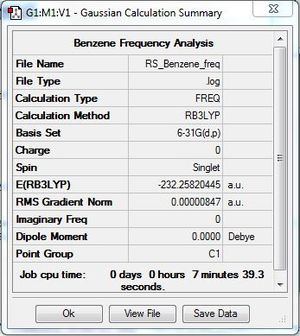
Frequency file: DOI:10042/31270 .

Frequency analysis was carried out to ensure that the optimised benzene molecule was at the minimum energy state. The low frequencies were within acceptable range and no negative frequencies were obtained for the second line. This ensured that the optimisation of the benzene molecule successfully found a minimum energy point.

Summary Data	Low Modes
	Low frequencies --- -3.9004 0.0004 0.0004 0.0009 5.4182 7.6326 Low frequencies --- 414.5262 414.5887 621.0907

Population Analysis

The MOs of benzene were computed and then viewed from the .fch file as follows. Population analysis file: DOI:10042/31278 .

From the visualisation of the MOs, it was noticeable that many of the valence MOs had sigma contributions and that the bonding was not as simplistic as depicted in most MO diagrams of benzene.

MO diagram

Center part of MO diagram of benzene

This MO diagram shows the real MOs based on calculations on the right side, and the LCAO MOs deconstructed from the real MOs on the left side. Only the valence orbitals are shown (MOs 7 to 27) as the core orbitals (MOs 1 to 6) are too deep in energy for interactions. The MO lowest in energy on the diagram is the totally symmetric sigma bonding MO. The MO highest in energy on the diagram is the pi antibonding unoccupied MO. It is interesting to note that the sigma antibonding orbitals are lower in energy than the pi antibonding orbitals. There are also other MOs which have overall antibonding character but are still relatively low in energy. Those with antibonding interactions through bonds are higher in energy than those with antibonding interactions through space. MOs with a larger number of nodes are higher in energy as there are more antibonding interactions within the MOs. For example, the e_1u bonding MOs have one nodal plane each, and are lower in energy than the e_2g bonding MOs which have two nodal planes each.

Relation to Aromaticity

Aromaticity is the delocalisation of electron density around a conjugated, planar ring of atoms. According to Hückel's rule, a cyclic molecule with 4n+2 π electrons (where n is an integer) is said to be aromatic. Benzene contains six pi electrons and follows the Hückel's rule for aromaticity where n=1, hence is considered to be aromatic. Its isoelectronic analogues, boratabenzne, pyridinium and borazine are also aromatic. Although the chemical structure of benzene is drawn to be a six carbon ring with three C=C bonds and three C-C bonds, it can be seen from the MOs that the electron density from the π bonds are spread out evenly around the whole bond. This can be seen most clearly in the pi totally bonding MO, while the π electron density is spread out evenly around the ring of six carbon atoms. While MOs contain formally only 2 electrons each, the distinction between the MOs are not clear in the real computed MOs, and the electron density is visualised as over the whole space of atoms in the MO diagram as shown above. Also, the presence of 6 πelectrons in benzene means that π bonding MOs, including the HUMO and the fully bonding π MO, are fully occupied and contribute to the overall stability of the molecule. If there were only 4 π electrons in the structure, the doubly degenerate HOMO would be each singly filled, leading to an unstable antiaromatic molecule as predicted by the Hückel's rule.

In addition, the MOs computed show that the aromatic stability of benzene is not only due to the π electrons occupying the bonding π MOs, but also due to the formation of strong σ bond within the σ framework. The six-membered ring is free of ring strain and the σ bonding and some antibonding MOs are lower in energy than the π MOs and are completely filled, contributing to the stability of the benzene molecule.

NBO Analysis

Charge Distribution	Specific NBO Charges
Charge Limits: -0.239 to 0.239	C: -0.239 H: 0.239

The charge distribution shows that carbon is more electronegative than hydrogen, hence it bears the negative charge in the molecule. The charges cancel out for each CH unit and since benzene is symmetrical about the C6 axis, the charge is evenly distributed throughout the molecule.

Based on the NBO analysis, it also can be seen that each carbon atom formed 3 essentially sp² hybrid orbitals which each interact with the sAO of one hydrogen atom and the sp² hybrid orbital of two adjacent carbons. Each carbon also has one unhybridised p orbital (100% p orbital) which forms the delocalised pi system. This p orbital has an occupancy of 1.67.

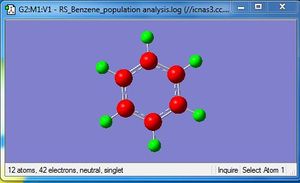
Boratabenzne Optimisation

B3LYP/6-31G(d,p)

Boratabenzene was optimised using the same method and basis set as for benzene.

Optimisation file: DOI:10042/31326 .

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000013 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES	Optimised Molecule

Frequency Analysis

Frequency file: DOI:10042/31332 .

Summary Data	Low Modes
	Low frequencies --- -7.2703 -0.0007 -0.0005 0.0007 3.1509 4.5207 Low frequencies --- 371.2965 404.4156 565.0825

The low frequencies were close to zero and showed that optimisation was successful.

Population Analysis

Population analysis file: DOI:10042/31333 .

MOs were visualised using the .fch file from the population analysis. It was observed that while the MOs were similar to those of benzene in terms of general ordering and nodes in MOs, the ordering of some MO levels were different and most importantly, MOs that were degenerate in benzene were no longer degenerate in boratabenzene due to the lack of symmetry, caused by the substitution of a boron atom for a carbon atom.

NBO Analysis

Charge Distribution	Specific NBO Charges
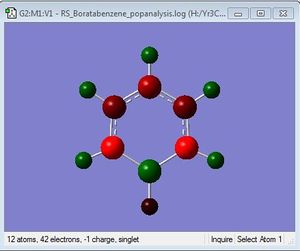
Charge Limits: -0.588 to 0.588	B:0.202 C: -0.340, -0.250, -0.588 H: 0.186, 0.179, 0.184, -0.096

The boron atom carries a positive charge as expected, as it is a less electronegative atom compared to carbon. The carbon atoms carry most of the negative charges within the molecule.

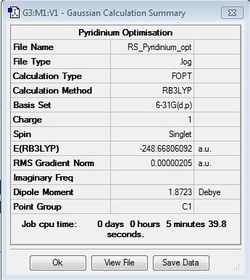
Pyridinium Optimisation

B3LYP/6-31G(d,p)

Pyridinium molecule was successfully optimised using the same method and basis set as benzene.

Optimisation file: DOI:10042/31341 .

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000010 0.000060 YES RMS Displacement 0.000004 0.000040 YES	Optimised Molecule

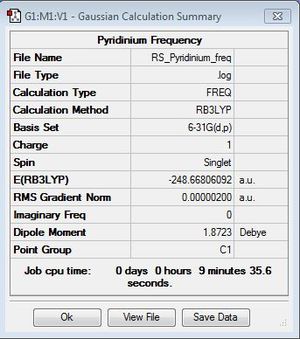
Frequency Analysis

Frequency file: DOI:10042/31270 .

Summary Data	Low Modes
	Low frequencies --- -9.3855 -2.9634 -0.0006 0.0005 0.0006 0.8971 Low frequencies --- 391.9002 404.3426 620.1994

Low frequencies were close to zero showing that a minimum energy state was successfully found for pyridinium.

Population Analysis

Population analysis file: DOI:10042/31360 .

The MOs were visualised using the .fch file from the population analysis. The energy levels of the MOs for pyridinium were lower in energy compared to those of benzene. This is consistent with what is expected as nitrogen being the more electronegative would have AOs deeper in energy as compared to carbon, hence overall the MOs are deeper in energy.

NBO Analysis

Charge Distribution	Specific NBO Charges
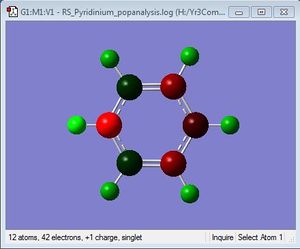
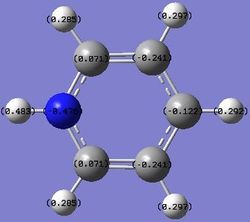
Charge Limits: -0.483 to 0.483	N: -0.476 C: 0.071, -0.241, -0.122 H: 0.483, 0.285, 0.297, 0.292

Nitrogen is shown to bear the largest negative charge as it is the most electronegative atom in the molecule. The charges on the atoms add up to +1, since pyridinium is a positively charged molecule, to make it isoelectronic with benzene.

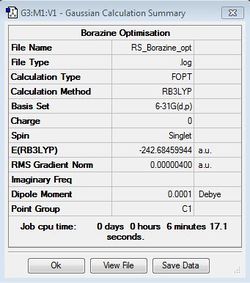
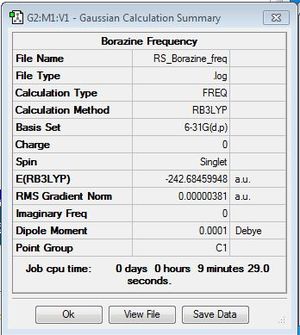
Borazine Optimisation

B3LYP/6-31G(d,p)

Borazine molecule was successfully optimised using the same method and basis set as benzene.

Optimisation file: DOI:10042/31340 .

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000009 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000027 0.000060 YES RMS Displacement 0.000008 0.000040 YES	Optimised Molecule

Frequency Analysis

Frequency file: DOI:10042/31346 .

Summary Data	Low Modes
	Low frequencies --- -7.2861 -0.0010 -0.0007 -0.0003 4.1726 7.4070 Low frequencies --- 289.5824 289.7072 404.4525

Low frequencies were within the acceptable range and hence showed that optimisation of borazine was successful in finding the minimum energy state.

Population Analysis

Population analysis file: DOI:10042/31360 .

MOs of borazine were visualised and were observed to show the most similarity to benzene among the three analogues in terms of energy levels and shapes of the MOs. This is probably due to the higher symmetry of borazine compared to the other two analogues.

NBO Analysis

Charge Distribution	Specific NBO Charges
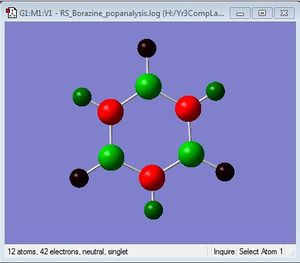
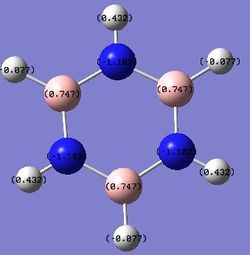
Charge Limits: -1.102 to 1.102	B: 0.747 N: -1.102 H: -0.077, 0.432

The charge distribution in borazine is as expected, with the more electronegative nitrogen atom bearing the negative charge and the less electronegative boron atom bearing the positive charge.

Comparison of Charge Distribution

	Benzene	Boratabenzene	Pyridinium	Borazine
Dipole Moment (Debye)	0.00	2.85	1.87	0.00
Charge Distribution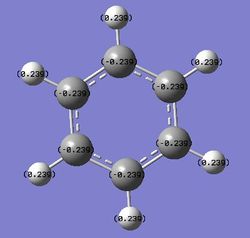
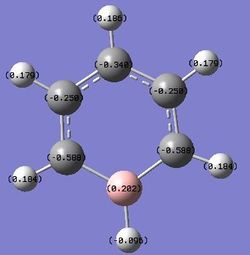
Specific NBO Charges	C: -0.239 H: 0.239	B:0.202 C: -0.340, -0.250, -0.588 H: 0.186, 0.179, 0.184, -0.096	N: -0.476 C: 0.071, -0.241, -0.122 H: 0.483, 0.285, 0.297, 0.292	B: 0.747 N: -1.102 H: -0.077, 0.432

Benzene is symmetrical about the C6 axis, hence it has an even charge distribution among the six carbon atoms and six hydrogen atoms and no dipole moment. Each carbon atom has a charge of -0.239 and each hydrogen atom has a charge of +0.239, showing that the electron density is on the carbon atoms, due to carbon being more electronegative than hydrogen. The charges cancel out and benzene is an overall neutral molecule.

Substituting one of the CH units for a BH and NH in boratabenzene and pyridinium respectively breaks the symmetry and causes an uneven charge distribution throughout the molecule, resulting in a dipole moment in both molecules. Nitrogen is more electronegative compared to carbon, while boron is less electronegative compared to carbon. In the images above, it can be clearly seen that the electron density is shifted to the more electronegative atoms in the molecule.

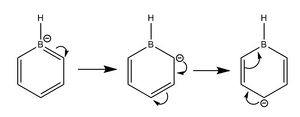
For boratabenzene, the electron density is shifted more to the five carbon atoms, while the boron atom bears a positive charge of +0.202. The hydrogen atom adjacent to the boron has a negative charge of -0.095, and is the only delta negative hydrogen in the molecule. This is because hydrogen is slightly more electronegative than boron, causing the B-H bond to be polarised. The carbon atoms adjacent to the boron atom each have a negative charge of -0.588, and are more negatively charged than the carbons which are two positions further away from the boron atom. This is due to the difference in electronegativity between carbon and boron, causing the C-B bond to be polarised as well, and hence the carbons are highly negatively charged. The carbon furthest away from boron is however more negatively charged than those in the meta positions, with a charge of -0.340. This is due to the resonance structures of boratabenzene, which the negative charge is on the ortho and para positions as shown below, so there is more electron density on the ortho and para carbon atoms. The other hydrogen atoms on the five carbon atoms are all positively charged, though less positively charged as compared to the hydrogen atoms in benzene. The charges on all the atoms add up to -1, as boratabenzene molecule bears an overall negative charge.

Resonance structures of boratabenzene

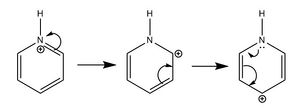
For pyridinium, the electron density is shifted more to the electronegative nitrogen atom, and it bears a negative charge of -0.476. The carbons at the ortho and para positions have a higher positive charge due to the resonance structures of pyridinium as shown above. The carbons are also positively charged due to the polarised C-N and the electron withdrawing effect of nitrogen. The hydrogen atom bonded to nitrogen is very positive, with a charge of +0.483, due to the electronegative nitrogen withdrawing electron density. The other hydrogen atoms each also carry a positive charge, but the charge gets smaller as the distance from the electronegative nitrogen increases. The charges on all the atoms add up to +1, as pyridinium molecule bears an overall positive charge.

Resonance structures of pyridinium

Borazine is a symmetrical about the C3 axis and hence charges cancel out around the ring of atoms and borazine has no dipole moment. The nitrogen atoms and boron atoms have charges of -0.102 and +0.747 respectively. These charges are observed to be of a higher value as compared to the nitrogen and boron atoms in boratabenzene and pyridinium and this is due to the increased difference in electronegativity between nitrogen and boron. This causes the B-N to be more polarised and the atoms to carry higher charges. Overall the charges cancel out and borazine is a neutral molecule.

Comparison of MOs

Three different MOs of benzene and its analogues were compared in the following tables.

	Benzene	Boratabenzene	Pyridinium	Borazine
Fully bonding pi MOs (17th MO)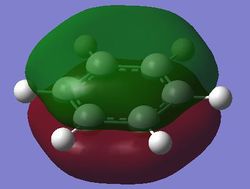
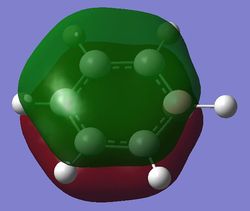
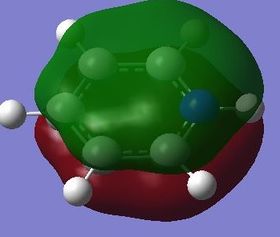
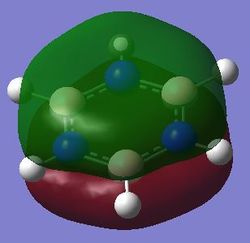
Energy (au)	-0.35994	-0.13210	-0.64062	-0.36133

The fully bonding pi MOs of the four molecules are shown as above. The electron density is spread over the top and bottom of the ring, with a nodal plane through the plane of the ring. For benzene each of the carbon atoms in the ring contribute one p orbital to this MO, and since the energy of the atoms are the same, the electron density is spread even over the plane. When the carbon atom is substituted by a more electropositive boron atom in boratabenzene, it is observed that the whole electron cloud is shifted slightly away from the boron atom. In pyridinium, the opposite is true; due to the electronegativity of nitrogen, more of the electron cloud is shifted towards the nitrogen atom. Hence for pyridinium and boratabenzene, the pi electron cloud is not symmetric about the axis perpendicular to the ring. The MO of borazine shows the same even spread of electron density as benzene due to the symmetry of the molecule. The energy of the MOs of benzene and borazine are about the same, while that of boratabenzene is higher and that of pyridinium is lower due to electronegativity differences.

	Benzene	Boratabenzene	Pyridinium	Borazine
Bonding pi MOs (20th MO)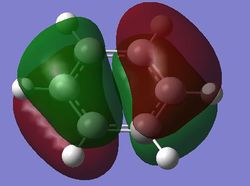
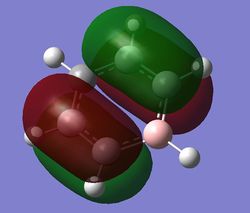
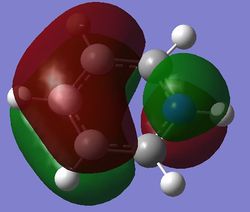
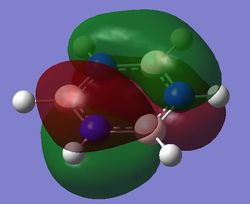
Energy (au)	-0.24690	-0.03492	-0.50847	-0.27594
Bonding pi MOs (21st MO)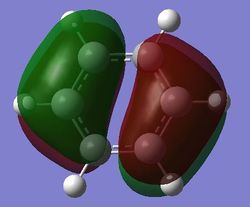
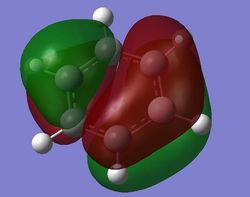
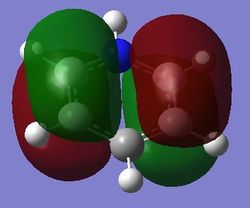
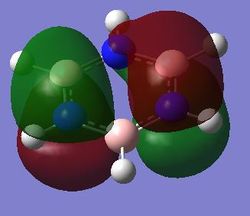
Energy (au)	-0.24690	0.01095	-0.47886	-0.27594

For benzene, the 20th and 21st MOs are degenerate and together form the HOMO. Each MO has a nodal plane through the plane of the ring and another nodal plane perpendicular to the plane of the ring. For the 21st MO, it can be seen that the nodal plane perpendicular to the plane of the ring runs through the centre of two carbon atoms, while for the 20th MO, the nodal plane perpendicular to the plane of the ring runs through two C-C bonds. The same is observed for pyridinium and borazine; however, the ordering of the two levels was swapped for boratabenzene. For boratabenzene, the 21st MO, not the 20th, contains the nodal plane that runs through two C-C bonds.

For benzene and borazine, the 20th and 21st MOs are degenerate due to the symmetry of the molecules. For pyridinium and boratabenzene, these two MOs are of different energy levels due to the difference in electronegativity of the two substituted atoms, causing the symmetry of the molecule to be disrupted. It can be observed that for the MOs of pyridinium and boratabenzne above, the two lobes are uneven in size. This is especially noticeable for the 21st MO of boratabenzene and the 20th MO of pyridinium. For boratabenzene, the three carbon atoms opposite the boron atom have a smaller lobe, while for pyridinium, the three carbon atoms opposite the nitrogen atom have a larger lobe. The difference is more distinctly seen in pyridinium as the electronegativity difference between C and N is larger.

Effects of substitutions on MOs

Boron, carbon and nitrogen are elements in the second row of the periodic table, with consecutive atomic numbers. Since electronegativity increases across the period, nitrogen is the most electronegative out of these three, and boron is the most electropostive. The difference in electronegativities account for many of the effects seen from substituting the atoms. The electronegativitities of the atoms are shown in the table below.

	Hydrogen	Boron	Carbon	Nitrogen
Pauling electronegativities values	2.20	2.04	2.55	3.04

Loss of degeneracy

Benzene is a highly symmetrical molecule and hence there are degenerate energy levels in the MO diagram. Replacing a CH unit with BH and NH in boratabenzene and pyridinium respectively breaks the D_6H symmetry of the molecule hence these energy levels are no longer degenerate in the MO diagram. Most of the MOs are similar in terms of shape, but the electron density and size of the lobes are slightly different, causing the MOs to have some variations in energy levels and to be no longer degenerate. The ordering of the MOs could also then be changed slightly. For borazine, some symmetry is lost due to the replacement of C-C units with B-N units; however, the molecule still has D_3H symmetry, so there is a lesser extent of degeneracy lost.

Differences in energy of the MOs

The energy of the AOs of boron, carbon and nitrogen follow the electronegativity trend of these atoms. Nitrogen is the most electronegative hence its AOs are deeper in energy. Hence when a carbon atom is replaced by a nitrogen atom in pyridinium, it is observed that the bonding MOs formed are generally lower in energy compared to those of benzene and nitrogen would be expected to have a larger contribution to the LCAO of the bonding MOs. For boratabenzene, it is observed that the energy levels of the MOs are mostly above 0, showing that they are higher in energy due to the boron AOs being higher in energy than that of carbon. The energy levels can be seen in the table below.

	Benzene	Boratabenzene	Pyridinium	Borazine
Energy Levels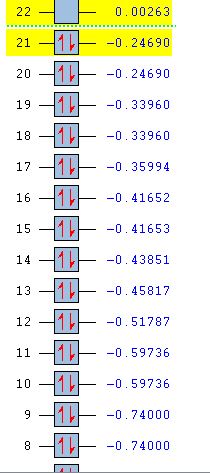
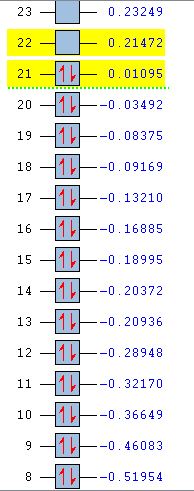
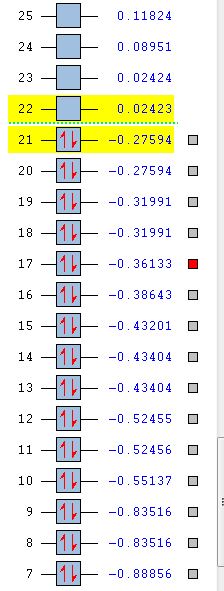