Rep:Mod:rr1210
All calculations were carried out using Gaussian on inputs generated in Gaussview 5.
BH3: Analysis of a simple molecule
Using the 3-21G basis set
A molecule of BH3 was created and each B-H bond set to an initial length of 1.5Å. A DFT optimisation was performed using the B3LYP method and 3-21G basis set.
Item Value Threshold Converged?
Maximum Force 0.000090 0.000450 YES
RMS Force 0.000059 0.000300 YES
Maximum Displacement 0.000352 0.001800 YES
RMS Displacement 0.000230 0.001200 YES
Predicted change in Energy=-4.580970D-08
Optimization completed.
-- Stationary point found.
Log file for BH3 optimisation.
B-H bond lengths: 1.19Å (lit: 1.19Å)[1] H-B-H angle: 120° (lit: 120°)[2]
From both the item table and the summary table gradient value we can see that the calculation has converged successfully. The values obtained for both bond lengths and angles match the literature values well.
Using the 6-31G(d,p) basis set
The log file from the optimisation using the 3-21G basis set was used as a starting point for a further optimisation using the 6-31G(d,p) basis set. The "nosymm" keyword was also added at this stage.
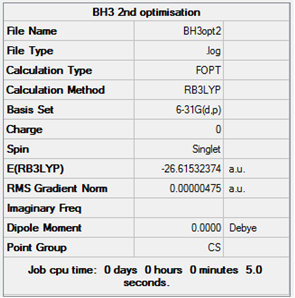
Item Value Threshold Converged?
Maximum Force 0.000010 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000039 0.001800 YES
RMS Displacement 0.000025 0.001200 YES
Predicted change in Energy=-5.356817D-10
Optimization completed.
-- Stationary point found.
Log file for the second BH3 optimisation.
B-H bond lengths: 1.19Å H-B-H bond angle: 120°
Comparing the calculation completed using the 3-21G basis set with the calculation using the 6-31G(d,p) set we can see that both the values in the item table and the gradient in the summary are much smaller for the 6-31G(d,p) which tells us that we are closer to the energy minimum for the molecule and therefore have a better optimisation than before.
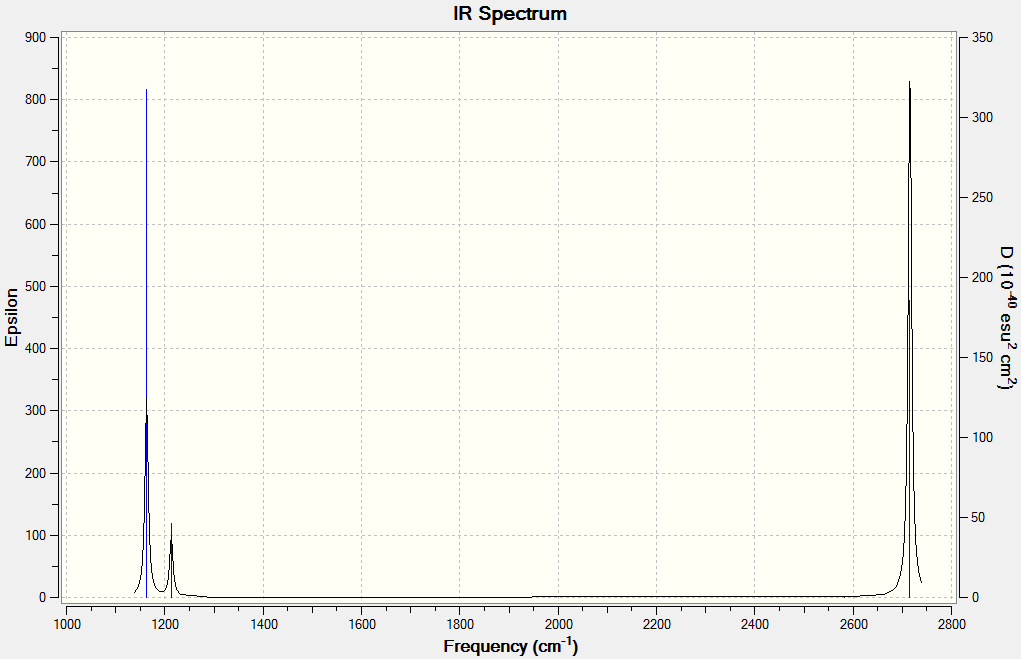
Frequency analysis
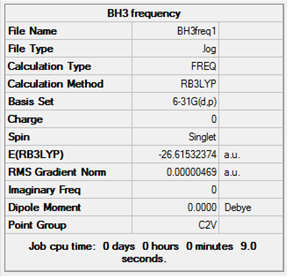
Log file for the frequency calculation of BH3.
Low frequencies --- -20.0769 0.0002 0.0004 0.0005 10.1432 10.2434 Low frequencies --- 1162.9613 1213.1631 1213.2257
| No. | Form of the vibration | Description of motion | Frequency | Intensity | Symmetry D3h |
|---|---|---|---|---|---|
| 1 |  |
The boron atom moves backward and forward, as do the hydrogen atoms, with the boron atom remaining equidistant from each hydrogen atom. The boron atom is furthest forward when the hydrogen atoms are furthest back. | 1163 | 93 | A"2 |
| 2 |  |
Two hydrogen atoms move up and down simultaneously, in the plane of the molecule. The remaining hydrogen and boron atom move up and down slightly, in the plane, opposing the motion of the other atoms. | 1213 | 14 | E' |
| 3 |  |
The boron atom is stable. One hydrogen moves from side to side in an extreme movement within the plane of the molecule. The other two hydrogen atoms move around the boron atom together, in the plane, following the movement of the top hydrogen atom. When the top hydrogen atom is furthest to the left, the other two hydrogen atoms are also at the leftmost point in their movement and vice verse. | 1213 | 14 | E' |
| 4 |  |
The boron atom is stable. All three hydrogen atoms simultaneously move in and out from the boron atom along the lines of their bonds. | 2582 | 0 | A'1 |
| 5 |  |
One hydrogen atom and the boron atom are stationary, whilst the other two move in and out from the boron atom along their bonds in an alternating fashion. | 2715 | 126 | E' |
| 6 |  |
The boron atom is stable, and all three hydrogen atoms move in and out along their bonds. Two move together, in opposition to the third. | 2715 | 126 | E' |
The six vibrations calculated only give three peaks in the IR spectrum because one is not IR active and there are two pairs of degenerate stretches which absorb at the same frequency, giving two peaks for four vibrational modes.
Molecular orbital diagram
The qualitative LCAO MO diagram shows large similarity to almost every calculated MO. This shows that LCAO is a useful technique, at least for smaller molecules.
TlBr3: Using pseudo potentials
Optimisation using LanL2DZ
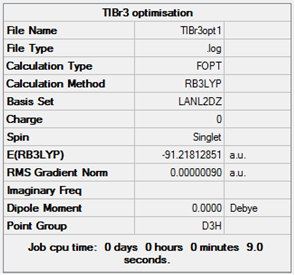
As thallium and bromine are heavy elements, in the sixth and fourth row of the periodic table respectively, pseudo potentials can be used within the basis set to approximate the effects of the many low energy atomic orbitals within the elements. This allows for much faster calculations on heavy elements. The basis set used was LanL2DZ.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.0842871D-11
Optimization completed.
-- Stationary point found.
Link to the calculation files on D-space.
Tl-Br distance: 2.65Å (lit: 2.52Å)[3] Br-Tl-Br Angle: 120° (lit:120°)[4]
The structure given (trigonal planar) agrees with the literature, however the bond lengths calculated are slightly longer than the literature value.
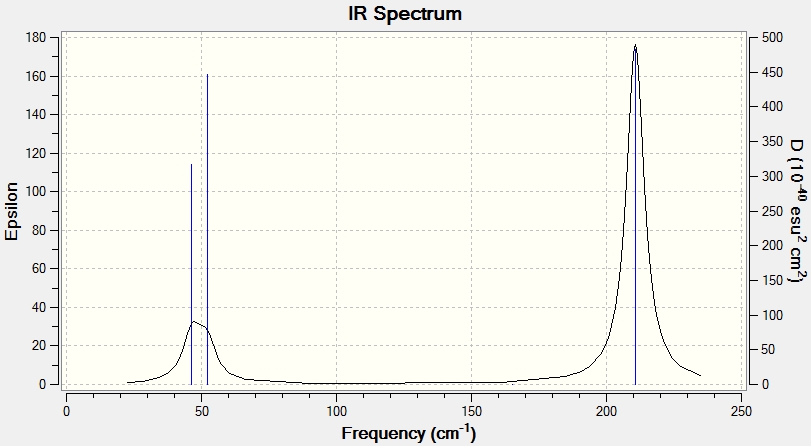
Frequency analysis
The frequencies of the optimised TlBr3 structure were calculated.
Link to the frequency calculation d-space.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
BBr3: Mixing basis sets and pseudo potentials
Optimising a Molecule of BBr3
As BBr3 has a mixture of small and large atoms, a mixture of basis sets and pseudo potentials was used. For the boron atom 6-31G(d,p) was used, and for the bromine atoms LanL2DZ was used.
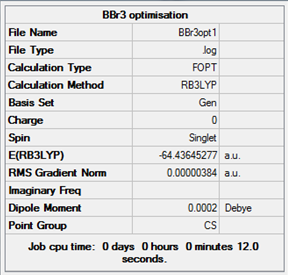
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000037 0.001800 YES
RMS Displacement 0.000024 0.001200 YES
Predicted change in Energy=-4.102661D-10
Optimization completed.
-- Stationary point found.
Log file for the optimisation of BBR3.
B-Br distance:1.93Å Br-B-Br Angle:120°
Comparing BH3, BBr3 and TlBr3 bond lengths and structures
| BH3 | BBr3 | TlBr3 |
|---|---|---|
| 1.19Å | 1.93Å | 2.65Å |
What difference does changing the ligand have? Changing the hydrogen atoms for bromine atoms gives a longer bond distance because bromine atoms are larger.
How are H and Br similar, how are they different? Both elements need to form a single covalent bond to get the right number of electrons, however bromine also has three lone pairs, two of which can back bond into the p-orbital of the boron atom, strengthening the bond.
What difference does changing the central element make?
Changing boron to thallium gives a longer bond distance, as thallium is a larger element.
How are B and Tl similar, how are they different?
Both elements are in group three and are therefore electron deficient. However thallium is a much larger element.
In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?
Gaussview does not draw a bond if the atoms are over an arbitrary distance apart. This doesn't mean there is no bond - just that the bond is long.
Comparing the vibrational modes of BH3 and TlBr3
| No. | Point group | Frequency in BH3 | Frequency in TlBr3 |
|---|---|---|---|
| 1 | A"2 | 1163 | 52 |
| 2 | E' | 1213 | 46 |
| 3 | E' | 1213 | 46 |
| 4 | A'1 | 2582 | 165 |
| 5 | E' | 2715 | 211 |
| 6 | E' | 2715 | 211 |
All the atoms in BH3 are much lighter than their counterparts in TlBr3, and this accounts for most of the differences in the vibrational modes and IR spectra. The period of a vibration is proportional to the weight of the two ends of the spring (using the ideal classical model) so therefore the frequency of a heavier ended spring will be lower. Overall this is the main change between the two spectra and so they are similar in ordering and in relative distances between vibrations.
There is one instance of reordering however, in going from BH3 to TlBr3 we see that the order of A"2 and E' is swapped.
NH3: NBO analysis
Optimisation
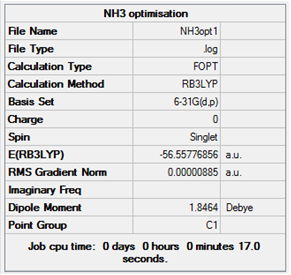
Log file for the optimisation of NH3.
Item Value Threshold Converged?
Maximum Force 0.000024 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000079 0.001800 YES
RMS Displacement 0.000053 0.001200 YES
Predicted change in Energy=-1.629727D-09
Optimization completed.
-- Stationary point found
Frequency calculation
Log file for the frequency calculation
Low frequencies --- -30.8045 -0.0014 -0.0008 -0.0007 20.2188 28.2150 Low frequencies --- 1089.5530 1694.1235 1694.1861
NBO analysis
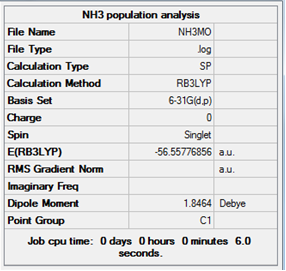
Log file for the population analysis of NH3.
The colour range is from +1 to -1. Nitrogen: -0.717 Hydrogen: +0.239
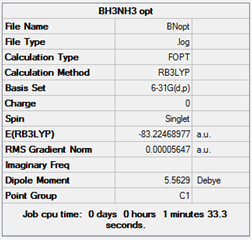
Association energies
The optimisation was again completed using b3lyp/6-31G(d,p) to allow for relevant comparison between products and reactants.
Item Value Threshold Converged? Maximum Force 0.000167 0.000450 YES RMS Force 0.000035 0.000300 YES Maximum Displacement 0.000915 0.001800 YES RMS Displacement 0.000403 0.001200 YES Predicted change in Energy=-1.161219D-07 Optimization completed. -- Stationary point found.
Link to the optimisation log file.
A frequency calculation was performed in order to check that the structure was optimised to a minimum rather than a maximum or stationary point.
Low frequencies --- -18.4759 -0.0012 -0.0010 -0.0010 9.5755 21.8281 Low frequencies --- 263.0781 631.3304 637.1936
E(BH3)= 26.61532374 E(NH3)= 56.55776856 E(NH3BH3)= 83.22468922
The separate molecules are 0.05159747au lower in energy. So breaking the bond between the two groups corresponds to a 135Kjmol-1 energy release.
Mini-project: Main group halides
In this project I will investigate the conformers, vibrations and MOs of the four isomers of Al2Cl4Br2, and find out which isomer is most stable.
Isomers and point groups
Below are the isomers under investigation, along with the point group assignments.
Optimisation
Each isomer was optimised using the full basis set 6-31G(d,p) on the aluminium and chlorine atoms and a pseudo potential LANL2DZdp on the bromine atoms. The table below contains the item and summary tables for each optimisation. To see the .log files for the calculations click the isomer number in the table. Isomer M is the monomer, optimised for comparison.
| Isomer | Summary table | Item table |
|---|---|---|
| 1 |  |
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000210 0.001800 YES RMS Displacement 0.000088 0.001200 YES Predicted change in Energy=-4.533044D-09 Optimization completed. -- Stationary point found. |
| 2 |  |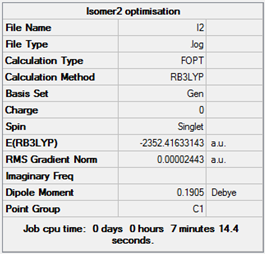
Item Value Threshold Converged? Maximum Force 0.000078 0.000450 YES RMS Force 0.000029 0.000300 YES Maximum Displacement 0.001248 0.001800 YES RMS Displacement 0.000569 0.001200 YES Predicted change in Energy=-9.764899D-08 Optimization completed. -- Stationary point found. |
| 3 |  |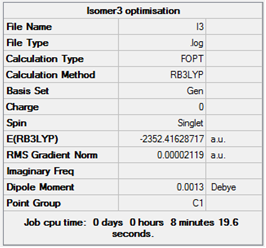
Item Value Threshold Converged? Maximum Force 0.000050 0.000450 YES RMS Force 0.000019 0.000300 YES Maximum Displacement 0.000597 0.001800 YES RMS Displacement 0.000288 0.001200 YES Predicted change in Energy=-3.860775D-08 Optimization completed. -- Stationary point found. |
| 4 |  |
Item Value Threshold Converged? Maximum Force 0.000097 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.001366 0.001800 YES RMS Displacement 0.000556 0.001200 YES Predicted change in Energy=-1.312890D-07 Optimization completed. -- Stationary point found. |
| M |  |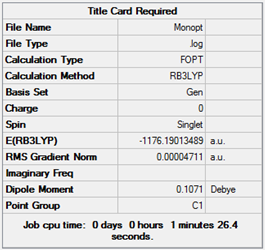
Item Value Threshold Converged? Maximum Force 0.000157 0.000450 YES RMS Force 0.000082 0.000300 YES Maximum Displacement 0.000757 0.001800 YES RMS Displacement 0.000570 0.001200 YES Predicted change in Energy=-1.010363D-07 Optimization completed. -- Stationary point found. |
Energies
| Isomer | Energy/KJmol-1 | Energy relative to isomer 1/KJmol-1 |
|---|---|---|
1.  |
6176242 | 0 |
2.  |
6176268 | 26 |
3.  |
6176268 | 26 |
4.  |
6176254 | 12 |
M.  |
6176180 | -62 |
From the energies computed it is found that the single monomer is approximately 60KJ/mol lower in energy, and therefore much more stable than the dimer. This matches with the observed lack of dimers of AlCl2Br in experiments/literature.
The most stable conformer has the bromine atoms in the bridging positions. As bromine is a larger atom it is probably most stable with two bonds than chlorine. This idea is supported by the second most stable isomer also having a bridging bromine, and the highest energy conformers having two bridging chlorine atoms.
The two conformers with two bridging chlorine atoms are similar in energy whether the bromine atoms are on the same or opposite sides, again supporting the idea that the stability is proportional to the number of bromine atoms bridging.
Frequencies
| Isomer | Summary table | Low frequency lines |
|---|---|---|
| 1 |  |
Low frequencies --- -2.4637 0.0028 0.0028 0.0030 2.0527 4.1270
Low frequencies --- 16.4709 63.6214 86.1342
|
| 2 |  |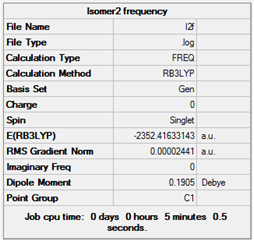
Low frequencies --- -3.9621 -0.7340 -0.0022 -0.0019 -0.0018 3.0162
Low frequencies --- 18.9792 51.1904 72.2557
|
| 3 |  |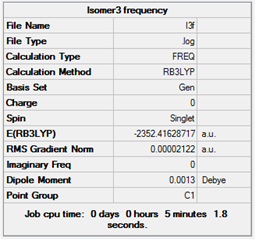
Low frequencies --- -5.0138 -0.1488 -0.0023 0.0014 0.0022 2.1597
Low frequencies --- 18.4967 49.1917 72.9216
|
| 4 |  |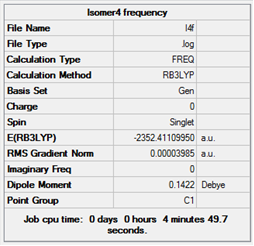
Low frequencies --- -2.6638 -1.3896 0.0019 0.0033 0.0036 3.6638
Low frequencies --- 17.2456 55.8013 80.0773
|
Isomer 1 IR spectrum
Isomer 2 IR spectrum
Isomer 3 IR spectrum
Isomer 4 IR spectrum
Comparison
| Isomer | Number of modes | Number of IR active modes |
|---|---|---|
1. |
18 | 9 (7 large) |
2. |
18 | 18 (12 large) |
3. |
18 | 11 (7 large) |
4. |
18 | 18 (12 large) |
Vibrational modes are only only visible in the IR spectrum if their motion causes the electric dipole of the molecule to change. For this reason the isomers with a lower symmetry group have the most peaks. Why this is can be seen easily in the case of isomer four which is C1; the low level of symmetry means the two bromine atoms are affected differently by every vibration and therefore every vibration changes the dipole moment and gives a peak.
MO calculation
The molecular orbitals of isomer 1, the most stable isomer, were calculated using an energy job, with the same 6-31G(d,p) and LanL2DZ basis set and pseudo potential combination. The keyword pop=full was used and NBO set to "full". Below is the summary table of the calculation. Link to the log
There are 124 molecular orbitals, of which 54 are fully occupied.
5 MOs visualised
| MO | Description of interaction |
|---|---|
13 |
The terminal chlorine atoms each have a p-AO. There are favourable through space interactions between the two chlorine atoms on each side of the molecule, and disfavourable through space interactions across the molecule. Overall the favourable interactions are stronger as the distance they bridge is shorter. Also the MO has all the electron density focused close to the electronegative chlorine atoms so it is very low in energy overall. |
23 |
There is a favourable, short, through space interaction between two s-AOs on the Aluminium atoms. |
29 |
There is something similar to a pi antibonding orbital on the two aluminium atoms. |
30 |
This is similar to a pi bonding orbital orbital on the aluminium atoms however is it slightly higher in energy than the 'antibonding' MO. |
53 |
This MO has p-AOs on each chlorine and bromine atom, arranged in mainly antibonding orientations, giving it a high energy. |
References
- ↑ Kawaguchi,Kentarou Journal of Chemical Physics, 1992, 96, 3411 - 3415
- ↑ Kawaguchi,Kentarou Journal of Chemical Physics, 1992, 96, 3411 - 3415
- ↑ Blixt, Johan; Glaser, J; Mink, J; Persson, I; Persson, P; Sandstroem, M Journal of the American Chemical Society, 1995, 117, 5089-5104
- ↑ Blixt, Johan; Glaser, J; Mink, J; Persson, I; Persson, P; Sandstroem, M Journal of the American Chemical Society, 1995, 117, 5089-5104