Rep:Mod:roguezimbo
Module One
Introduction
The aim of computational chemistry within the organic synthesis is to model structure and reactivity of organic molecules. In this wiki, two methods are implemented for the computational analysis of organic molecules: MM2 (molecular mechanics) and DFT-based molecular orbital theory.
The MM2 procedure only calculates the potential energy of the molecule, and is based on the following assumptions[1]
1. Nuclei and electrons are considered as single particles
2. Atoms are treated as spheres
3. Bond angle bending, bond stretching, bond torsion (twisting) and through space (non-bonded) interactions are all defined by separate potential functions, all of which are defined by empirically derived parameters (bond force constants/equilibrium values/Leonard-Jones Potential)
The overall potential energy of the molecule is then defined as the sum of 6 terms:
Potential energy = Stretch + Bend + Stretch-bend + Torsion + Non-1,4 van der Waals + 1,4-van der Waals + dipole/dipole
· Stretch – represents the energy required to change the bond length.
· Bend – represents the energy required to distort the bond angle from the optimal value.
· Torsion – represents the energy required to twist the bond from the ideal/minimum energy conformation.
· Non-1,4 van der Waals – represents the energy for through space interactions between pairs of atoms that are separated by more than 3 atoms.
· 1,4-van der Waals – represents the through space interaction for atoms separated by 2 atoms or less.
· Dipole/dipole – represents the energy resulting from the interaction of bond dipoles.
Modelling Using Molecular Mechanics
The Hydrogenation Of Cyclopentadiene Dimers
At temperatures above -80⁰[2], cyclopentadiene will thermally react in a diels alder reaction to form a dimer, which exists as one of two possible isomers, the exo- form and the endo- form:

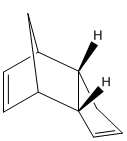
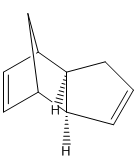
From a thermodynamic point of view, the exo-dimer is the more stable dimer, as shown by steric energy calculations using MM2 calculations on ChemBio3D:
| Structure | Exo-dicyclopentadiene (kcalmol-1) | Endo-dicyclopentadiene (kcalmol-1) | Difference In Energy (kcalmol-1) |
| Stretch (kcal/mol) | 1.2848 | 1.2503 | 0.0345 |
| Bend (kcal/mol) | 20.5795 | 20.8492 | -0.2697 |
| Stretch-Bend (kcal/mol) | -0.8379 | -0.8357 | -0.0022 |
| Torsion (kcal/mol) | 7.6559 | 9.5109 | -1.855 |
| Non-1,4-VDW (kcal/mol) | -1.4174 | -1.5434 | 0.126 |
| Total Energy (kcal/mol) | 31.8765 | 33.9975 | -2.121 |
The reason that the endo-product is thermally more is due to 1,4 strain carbons on the two rings, which is lees sever than the 1,4,-strain between the analogous carbon and hydrogen in the endo-product:


As shown, the exo-dimer is more thermodynamically stable molecule by a value of 2.121kcalmol-1. However, experimentation1 shows that, at room temperature and pressure, thermal dimerization of cyclopentadiene results in a ratio of 99.5:1 products, in favour of the endo-product.
This is because the transition state for the formation of the endo-product is lower in energy than that of the exo-product, and, at room temperature, the reaction is irreversible hence the kinetic endo- Normal 0 false false false EN-GB X-NONE X-NONE product is dominantly formed. The transition state is stabilised by secondary orbital interactions stabilising the transition state, allowing faster formation of the product2. The mechanism of the dimerization is as follows[3]:

Hydrogenation Of Endo-Product
There are 2 alkene links in the endo-cyclopentadiene dimer which can be hydrogenated, and so partial hydrogenation can result in one of two possible isomers:

The steric energies of the 2 possible products were calculated as before:
| Structure | Product 4 (kcalmol-1) | Product 3 (kcalmol-1) | Difference (kcalmol-1) |
| Bend | 14.5232 | 18.9396 | -4.4164 |
| Stretch-Bend | -0.5492 | -0.7609 | 0.2117 |
| Torsion | 12.4981 | 12.1275 | 0.3706 |
| Non-1,4 VDW | -1.0693 | -1.5068 | 0.4375 |
| 1,4-VDW | 4.5117 | 5.7293 | -1.2176 |
| Dipole/Dipole | 0.1406 | 0.1613 | 0.2493 |
| Total Energy | 31.1521 | 35.9266 | -4.7745 |
The energy calculations show that product 1 is the thermodynamically more stable dihygrogenated product by a value of 4.4164kcalmol-1. The dominant factor in determining the more stable product is the difference in bending energy- the bend energy of product 2 is larger than that of product 1 by a value of 4.4164kcalmol-1 because of strain on the remaining C=C double bond. The orbitals of each of the alkenes are sp2 hybridized, and so the ideal bond angle between each of the groups attached to the two carbons is 120⁰. MM2 measurements of ChemBio3D shows that the angle between the carbons on product 1 is 112.4⁰ and on product 2 is 107.6⁰, resulting in more severe strain on product 2 than product 1. Product 1 is therefore the more thermodynamically stable product for this reason.
Stereochemistry And Reactivity Of An Intermediate In The Synthesis of Taxol
A precursor for Taxol (an anti-cancer drug) is an oxy-cyclodecene based structure, which exists as one of two possible isomers:
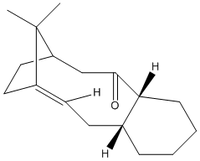

MM2 measurements of the energy of the isomers resulted in the following:
| Structure (kcalmol-1) | Up Isomer (kcalmol-1) | Down Isomer (kcalmol-1) |
| Stretch | 2.7847 | 2.6211 |
| Bend | 16.5425 | 11.3404 |
| Stretch-bend | 0.43 | 0.344 |
| Torsion | 18.2561 | 19.661 |
| Non-1,4 VDW | -1.5578 | -2.1577 |
| 1,4-VDW | 13.1091 | 12.8714 |
| Dipole/dipole | -1.725 | -2.0022 |
| Total energy | 47.8396 | 42.683 |
Overall, the “down” isomer is the more stable isomer, by a value of 5.1566. The dominant term in the energy difference between the two molecule is the bend energy- the difference between the two products is 5.2058kcalmol-1- the difference is due to the strain carbonyl carbon- it is an sp2 hybridised atom hence the ideal bond angle is 120⁰. The C-C-C bond angle for the “down” isomer is 119.7⁰, very close to the ideal angle of 120⁰. The C-C-C bond angle for the “up” isomer, however is 126⁰ which is a very large distortion, resulting in a large steric strain on the molecule and destabilisation of the overall structure relative to the “down” isomer:


The “olefin strain energy” is defined as the difference between the strain energy of an olefin and that of the alkane it is derived from[4] . The hydrogenated products for the 2 isomers are as follows:


The energies of the hydrogenated products are as follows:
| Structure | Hydrogenated Up isomer (kcalmol-1) | Hydrogenated Down Isomer (kcalmol-1) |
| Stretch | 2.9708 | 2.8479 |
| Bend | 17.6675 | 14.2295 |
| Stretch-Bend | 0.6802 | 0.6663 |
| Torsion | 23.0706 | 22.1011 |
| Non-1,4 VDW | -1.442 | -2.6437 |
| 1,4-VDW | 16.1262 | 15.8816 |
| Dipole/dipole | -1.7739 | -1.7261 |
| Total energy | 57.2994 | 51.3566 |


The olefin strain energy of the alkenes 9 and 10 are therefore:
Olefin strain energy of 9 = 47.8396 - 57.2994 = -9.4598kcalmol-1
Olefin strain energy of 10 = 42.6830 - 51.3566 = -8.6736kcalmol-1
These two isomers are examples of hyperstable olefins- the alkene forms are more stable than the alkane forms which they are derived from. The main source of this difference in strain energy is due to 2 reasons:
1. Additional Van der Waal forces between hydrogen atoms of the molecules in the alkane which are not present in the alkene. The Van der Waal radius of hydrogen is 1.05Å- hence, any 2 hydrogens which are less than 2.10Å from each other will experience repulsive Van Der Waal forces, destabilising the molecule. Below are pictures of the molecules, where destabilising Van der Waal forces are present in the alkane which were not present in the alkene:
  |
2. Additional torsional energy in the alkane, which occurs at the previous bridgehead alkene carbon:


An ideal sp3 C-C-C bond angle is 109.4⁰. The above images show that the C-C-C angles at the carbon for molecules 9 and 10 are 119.2⁰ and 118.8⁰- both of which are far from the ideal angle, resulting in destabilisation of the molecule in the form of steric torsional energy.
Modelling Using Semi-Emperical Molecular Orbital Theory
Computational chemistry can also be used to estimate electron densities and molecular orbitals: this is of vital importance in consideration of chemical reactivity of the molecule. MM2 calculations are of little use in this case, as it will only calculate the steric energies of the molecule, ignoring any electronic factors.
Regioselective Addition of Dichlorocarbene
The two alkene bonds found in the bicyclo-compound 12 are found to react at different rates upon addition of electropillic compounds, such as dichlorocarbene4: the C=C bond which is endo- to the chlorine is found to react before the exo- C=C bond:

Initial MM2 minimisation of the unreacted diene molecule resulted in the following energies:
| Structure | Bicyclohexadiene molecule (kcalmol-1) |
| Bend | 4.7308 |
| Stretch-bend | 0.0397 |
| Torsion | 7.6623 |
| Non-1,4 VDW | -1.0641 |
| 1,4-VDW | 5.7953 |
| Dipole-dipole | 0.1124 |
| Total energy | 17.8945 |
Measurement of the C-C=C bond angles on each of the two sides of the molecule gives results of 123.7⁰ for the C=C bond which is endo- to the chlorine and 123.2⁰ for the bond exo- to the chlorine. Both of these results are very similar, and so any steric strain on the double bonds are approximately equivalent. Therefore, steric energy calculations using MM2 cannot be used to rationalise the difference in reactivity between the two bonds.
Molecular orbital theory and calculation of the distribution of electron density is therefore required for this problem. Electophillic addition occurs due to interaction of the HOMO of the alkene during the electrophilic addition of the carbene. PM6 calculations of the HOMO resulted in the following molecular orbital:

The molecule is of CS symmetry (E, σh). However, this molecule has no mirror line of symmetry (σh) and is therefore not an applicable calculation of the HOMO molecular orbital. The calculation was therefore repeated, using RM1 procedure, yielding the following molecular orbitals:





The HOMO of the molecule, as shown, is mainly found on the C=C bond endo- to the chlorine- henceforth, the alkene link endo- to the chlorine is more susceptible to electrophilic attack.
Consider the HOMO of the same molecule, except the chlorine has been replaced with a hydrogen:
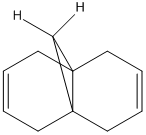

As shown, the HOMO is spread over both of the alkene links equally. As a result, both of the alkene links are isoenergetic and equally reactive towards electrophilic attack. Literature shows4 that the chlorine atom lowers the energy of the exo-alkene due to a secondary orbital interaction between the C-Cl σ* and the C=C bond, therefore lowering the energy of the C=C bond:

Infrared Analysis
Consider the dihydrogenated form of the bicyclohexadiene, compound 13:
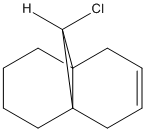
The IR scans of compounds 12 and 13 were calculated using the Gaussian interface and the C=C and C-Cl are recorded below:
| Compound | 12 | ' | 13 | ' |
| Frequency/cm-1 | Stretching mode | Frequency/cm-1 | Stretretching mode | |
| C-Cl | 770.86 |  |
774.87 |  |
| C=C (endo-) | 1757.35 |  |
1758.1 |  |
| C=C (exo-) | 1737.03 |  |
N/A |
As expected, the C-Cl bond is at a higher vibrational frequency. This is because the exo- C=C π bond is no longer present to overlap with the C-Cl σ* orbital, thereby weakening the C-Cl bond and lowering the stretching frequency.
The endo- alkene bond is almost unaffected by the change, because there was no orbital overlap with the exo- bond. Any change in the vibrational frequency is due to steric changes within the molecule.
The overall IR of the two compounds 12 and 13 are:


Monosaccharide Chemistry: Glycosidation
Glycosiation is a reaction in which a leaving group on the anomeric centre of a sugar via nucleophillic attack:

The easiest method for selectively preparing either the α-anomer or the β-anomer is by using neighbouring group participation- by choosing the group R’ so as to stabilise the intermediate so as to favour one of the isomers. One of the most common R’ groups is the acetyl group, -OC(O)CH3:

Axial Acetyl Group
If the acetyl group is on the axial position, the C=O bond of the acetyl group can be situated above the plane of the oxonium C=O bond (termed conformer A) or below the plane of the oxonium C=O bond (termed conformer A’):
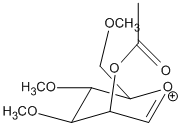

Energy calculation using MM2 and heat of formation calculation using MOPC/PM6 yielded the following results:
| Structure | A (kcalmol-1) | A’ (kcalmol-1) |
| Stretch | 2.5355 | 2.5737 |
| Bend | 12.1904 | 8.5122 |
| Stretch-bend | 1.003 | 0.9272 |
| Torsion | 1.715 | 3.1857 |
| Non-1,4 VDW | -0.2623 | -2.3521 |
| 1,4-VDW | 18.8428 | 19.2732 |
| Charge/Dipole | -18.6513 | -1.6125 |
| Dipole/Dipole | 7.7557 | 3.0066 |
| Total Energy | 25.1262 | 33.513 |
| Heat of formation (MOPAC/PM6) | -91.66198 | -77.17801 |
As expected, conformer A is more stable, because of the stabilising interaction between the axial O lone pair and the π* C=O bond.
Upon nucleophillic addition of the acetyl group onto the oxonium C=O results in 2 possible conformers, C and C’:

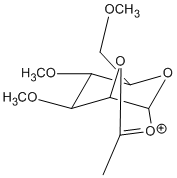
Energy calculations of the two conformations and heat of formation using MOPAC/PM6 yielded the following results:
| Structure | C (kcalmol-1) | C’ (kcalmol-1) |
| Stretch | 1.9792 | 2.7039 |
| Bend | 12.5544 | 18.1056 |
| Stretch-bend | 0.7129 | 0.8173 |
| Torsion | 7.6314 | 8.1949 |
| Non-1,4 VDW | -3.3549 | -3.4449 |
| 1,4-VDW | 17.8067 | 19.5065 |
| Charge/Dipole | -7.4317 | -0.4366 |
| Total Energy | 29.4266 | 44.5317 |
| Heat of formation (MOPAC/PM6) | -91.6682 | -69.47866 |
The conformer C is more therefore more stable, because C' is destabilised by ring torsion around the 5-membered ring.
It should be noted that the heat of formation for A is -91.66198 and for C is -91.6682: the two isomers are within 0.00622Kcalmol difference in energy. This is because there is very little change in the conformation of the molecules:- the O=C O angle in isomer A is 104.7⁰ and the O C non-bonded distance is 1.599A. In C isomer, the O=C-O angle is 104.7⁰ and the O-C bond distance is 1.599A:


As there is a great deal of overlap between the lone pair of the acetyl O and the π* orbital of the oxonium C=O in isomer A, (angle between them= 104.7⁰; maximum overlap occurs at 107⁰ according to Burgi-Dunitz theory) the short non-bonded distance between anomeric C and acetyl O is stabilised.
On the other hand, the heat of formation of A’ is and for C’-77.17801 is -69.47866. There is a large difference between the two values in this case (7.69935kcalmol-1). This is because there is a very large difference in the conformations of the molecules: the O=C O angle for A’ is 156.2⁰ and the non-bonded C O distance is 3.558A- both values are too large for overlap. For C’ on the other hand, the O=C-O bond angle is 113.1⁰ and the anomeric C- acetyl O bond distance is 1.586A. Despite the additional orbital overlap, the molecule is overall destabilised due to additional ring torsion at the acetyl bond while forming the 5-membered ring.
Equatorial Acetyl Group
A similar argument can be applied to this case where there are 2 possible conformations for the initial oxonium ion, B and B’:
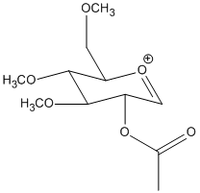
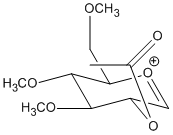
Energies of the 2 molecules are as follows:
| Structure | B (kcalmol-1) | B’ (kcalmol-1) |
| Stretch | 2.6128 | 2.3548 |
| Bend | 12.1328 | 9.5017 |
| Stretch-bend | 1.0387 | 0.8042 |
| Torsion | 1.1901 | 1.8317 |
| Non-1,4 VDW | -1.0164 | -2.231 |
| 1,4-VDW | 17.9419 | 19.4949 |
| Charge/Dipole | -9.1936 | -9.6778 |
| Dipole/Dipole | 5.5126 | 5.6447 |
| Total Energy | 30.2188 | 27.7232 |
| Heat of formation (MOPAC/PM6) | -88.73046 | -75.39869 |
As expected, conformer B is more stable (more negative heat of formation), because of the stabilising interaction between the axial O lone pair and the π* C=O bond. These conformers highlights the reason why MM2 is unreliable for these calculations: MM" relies only on steric energies to predict the overall energy of the molecule, ignoring these important secondary orbital overlaps.
Upon nucleophillic addition of the acetyl group onto the oxonium C=O results in 2 possible conformers, D and D':
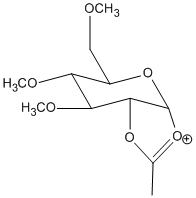

Energies of the two conformations are as follows:
| Structure | D (kcalmol-1) | D’ (kcalmol-1) |
| Stretch | 2.0818 | 2.7356 |
| Bend | 19.676 | 22.1463 |
| Stretch-bend | 0.7677 | 1.0431 |
| Torsion | 8.6644 | 8.1302 |
| Non-1,4 VDW | -2.3999 | -2.4564 |
| 1,4-VDW | 17.4026 | 18.2471 |
| Charge/Dipole | -10.2949 | -2.1477 |
| Dipole/Dipole | -0.3835 | -0.9213 |
| Total Energy | 35.143 | 46.7786 |
| Heat of formation (MOPAC/PM6) | -88.40613 | -64.68683 |
Again, conformer D is more stable than conformer D'.
Analogous to the axial acetyl group, B and D are almost isoenergetic (energy difference of 0.32433) due to only a very small difference i conformations. On the other hand, B' and D' are both very different in energy, due to a large change in conformation resulting in increased ring torsion around the 5-membered ring.
Mini-Project: The Total Synthesis of (-)-Cubedol
Cubedol is an organic alcohol which was prepared and examined in detail by D.M. Hodgson et al.[5]:

In order to investigate the spectroscopic properties of the molecule, the conformational energy was first minimised using MM2 on ChemBio3D, resulting in the following structure:
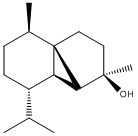
The MM2 energy of the molecule is as follows:
| ' | Cubidol (kcalmol-1) |
| Stretch | 2.2453 |
| Bend | 9.661 |
| Stretch-bend | -0.5152 |
| Torsion | 20.9702 |
| Non-1,4 VDW | -3.5165 |
| 1,4 VDW | 9.678 |
| Dipole/dipole | 0.3501 |
| Total energy | 38.873 |
The conformational energy was then minimised using the Gaussian procedure. Using Gaussian, the NMR; IR and optical rotation were then measured and compared to the literature values.
Infrared Analysis
Infrared analysis of the molecule resulted in the following overall IR:

Tabulated below are selected computationally measured stretching frequencies, and the stretching frequencies as measured by Hodson et al.:
As shown, the computationally measured values are in agreement with the literature values for all but one of the measurements: the O-H stretch. The O-H stretching frequency is highly dependent on the solvent (ie. Whether H-bonding or not), and the computationally measured method did not bring into account the solvent.
NMR Analysis
The calculated 13C NMR of the compound is as follows:

13C NMR was measured using Gaussian. Tabulated below are the literature and calculated values:

| Carbon | Gaussian calculated/ppm | Literature/ppm | Error |
| 1 | 41 | 33.4 | -7.6 |
| 2 | 40.1 | 29.5 | -10.6 |
| 3 | 50.2 | 36.3 | -13.9 |
| 4 | 78.8 | 80.3 | 1.5 |
| 5 | 37.3 | 39 | 1.7 |
| 6 | 35.3 | 22.6 | -12.7 |
| 7 | 39.5 | 44.1 | 4.6 |
| 8 | 20.5 | 26.4 | 5.9 |
| 9 | 25 | 31.7 | 6.7 |
| 10 | 31.9 | 30.8 | -1.1 |
| 11 | 30 | 33.6 | 3.6 |
| 12 | 21.1 | 18.7 | -2.4 |
| 13 | 31.4 | 27.9 | -3.5 |
| 14 | 23 | 20.1 | -2.9 |
| 15 | 21.3 | 19.6 | -1.7 |
As shown, the calculated NMR values for the attached methyl groups (C11 and C12) and the iso-propyl group (C13, C14 and C15) are all accurate (within 5 ppm of literature values), because there are not many possible conformations. However, the NMR measurements of the carbons in the two cyclohexane rings are very inncaurate due to the many possible configurations of the ring.
- ↑ ChemBio3D Help Index: MM2 dynamics
- ↑ Malgorzata Jamróz, Slawomir Galka, Jan Dobrowolski, Journal of Molecular Structure, 2003, (634), 225-233.DOI:10.1016/S0166-1280(03)00348-8 10.1016/S0166-1280(03)00348-8
- ↑ Waren, Wothers, McLaden and Greeves, Organic Chemistry, p. 915.
- ↑ Willhelm Maler and Paul von Ragué Schleyer, J. Am. Chem Soc., 1981 (103), 1891-1900.DOI:10.1021/ja00398a003
- ↑ David M. Hodgson, Saifullah Salik and David J. Fox, Journal of Organic Chemsitry,2010, 75 (7), 2157-2168.DOI:10.1021/jo9022974




