Rep:Mod:rkf75
BH3
Optimization and Frequency calculations
Method- RB3LTP
Basis set- 6-31G(d.p)
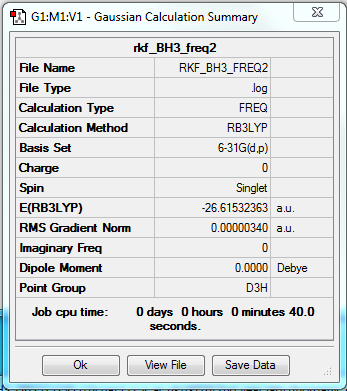
File- File:RKF BH3 freq.log
Low frequencies --- -0.6577 -0.3697 -0.0054 13.3878 16.8566 16.8694 Low frequencies --- 1163.0432 1213.2142 1213.2169
Item Value Threshold Converged?
Maximum Force 0.000007 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000027 0.001800 YES
RMS Displacement 0.000013 0.001200 YES
Predicted change in Energy=-2.724889D-10
Optimization completed.
-- Stationary point found.
Vibrations
Frequency IR Intensity IR active Vibration type 1163 93 Yes Symmetric bend 1213 14 Yes Symmetric bend 1213 14 Yes Anti symmetric bend 2582 0 No Symmetric stretch 2715 126 Yes Anti symmetric stretch 2715 126 Yes Anti symmetric stretch
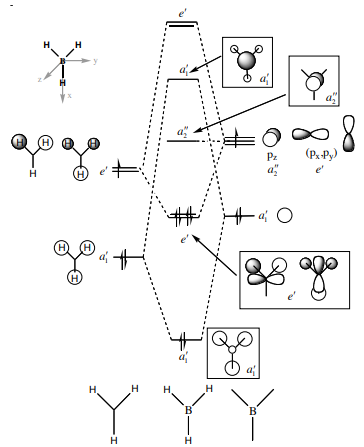
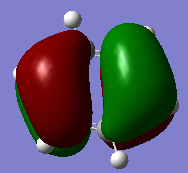
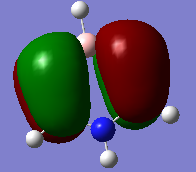
Molecular Orbitals
Molecular orbital diagram for BH3 [1]
a1' orbital comparison
e' orbital comparison
LUMO orbital comparison
There is no significant difference in these diagrams suggesting that qualitative MO theory is useful and quite accurate.
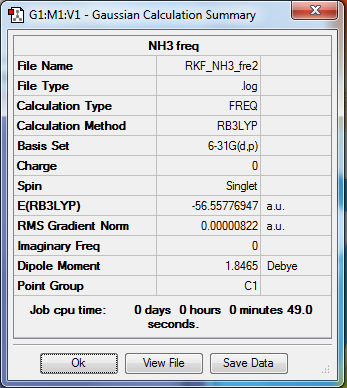
NH3
Optimization and Frequency calculations
Method- RB3LTP
Basis set- 6-31G(d.p)
File- File:RKF NH3 FRE2.LOG
Low frequencies --- -18.4182 -0.0006 0.0004 0.0004 20.7066 60.3683 Low frequencies --- 1089.5087 1694.0771 1694.1906
Item Value Threshold Converged?
Maximum Force 0.000016 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000039 0.001800 YES
RMS Displacement 0.000017 0.001200 YES
Predicted change in Energy=-5.925237D-10
Optimization completed.
-- Stationary point found.
NH3BH3
Optimization and Frequency calculations
Method- RB3LTP
Basis set- 6-31G(d.p)
File- File:RKF NH3BH3 FRE.LOG
Low frequencies --- -0.0009 -0.0008 0.0004 18.0575 28.4116 40.0963 Low frequencies --- 266.4888 632.3850 639.5950
Item Value Threshold Converged?
Maximum Force 0.000114 0.000450 YES
RMS Force 0.000062 0.000300 YES
Maximum Displacement 0.000701 0.001800 YES
RMS Displacement 0.000431 0.001200 YES
Predicted change in Energy=-1.783463D-07
Optimization completed.
-- Stationary point found.
Energy Calculations for NH3BH3
E(NH3)= -56.55776947 a.u.
E(BH3)= -26.61532363 a.u.
E(NH3BH3)= -83.22469072 a.u.
ΔE=[E(NH3)+E(BH3)]-E(NH3BH3)= (-26.61532363-56.55776947)+83.22469072= 0.05159762 a.u. = 135.47 kJ mol -1
The energy of C-C bond is around 350 kJ mol-1 and so this bong is much weaker in comparison
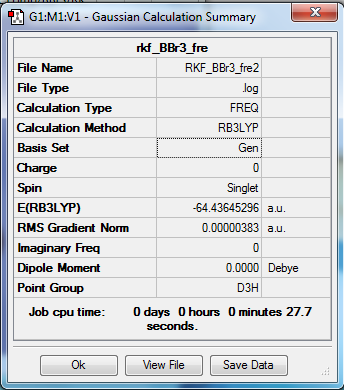
BBr3
Optimization and Frequency calculations
Method- RB3LTP
Basis set- Gen
File- File:RKF BBr3 fre2.log
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000018 0.001200 YES
Predicted change in Energy=-4.106155D-10
Optimization completed.
-- Stationary point found.
Benzene
Optimization and Frequency calculations
Method- RB3LTP
Basis set- 6-31G(d.p)
File- File:Rkf 1BEN FRE.LOG
Low frequencies --- -11.6728 0.0003 0.0003 0.0004 6.6686 15.6846 Low frequencies --- 414.0392 414.6031 621.0860
Item Value Threshold Converged?
Maximum Force 0.000193 0.000450 YES
RMS Force 0.000094 0.000300 YES
Maximum Displacement 0.000787 0.001800 YES
RMS Displacement 0.000368 0.001200 YES
Predicted change in Energy=-4.828252D-07
Optimization completed.
-- Stationary point found.
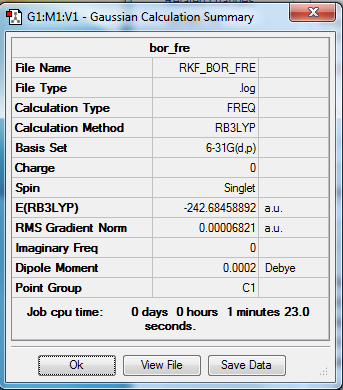
Borazine
Optimization and Frequency calculations
Method- RB3LTP
Basis set- 6-31G(d.p)
File- File:RKF BOR FRE.LOG
Low frequencies --- -15.9978 -11.0410 -0.0015 -0.0014 -0.0012 4.1543 Low frequencies --- 288.8151 289.7885 404.2303
Item Value Threshold Converged?
Maximum Force 0.000203 0.000450 YES
RMS Force 0.000068 0.000300 YES
Maximum Displacement 0.000362 0.001800 YES
RMS Displacement 0.000136 0.001200 YES
Predicted change in Energy=-1.262843D-07
Optimization completed.
-- Stationary point found.
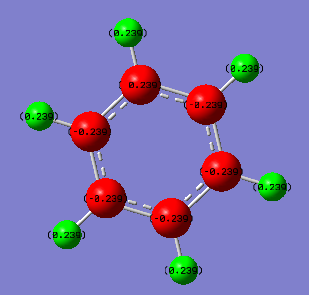
Charge Distribution in Benzene and Borazine
Benzene Borazine
C atoms = -0.084 N atoms = -0.471
B atoms = +0.307
H atoms = +0.084 H(N) atoms = +0.250
H(B) atoms = -0.087
Carbon and hydrogen have similar electronegativities and therefore the charge difference is very small. Carbon is more electeronegative and therefore ends up with a small negative charge. The symmetry of benzene means that all hydrogen atoms have the same charge.
In borazine nitrogen is more electronegative than hydrogen but boron is less electronegative than hydrogen. This results in hydrogen having both negative and positive charges depending on its position around the ring. Boron and hydrogen have electronegativities even more similar than carbon and hydrogen and therefore the hydrogens bonded to boron have an even smaller charge than in benzene. The boron atoms are experiencing the electronegativity difference from both bonded nitrogen atoms as well as the small impact from the hydrogen resulting in boron having a much larger charge. Nitrogen is significantly more electronegative than every other atom present resulting in a strong negative charge.
Compared to benzene, borazine contains significantly stronger charges and less symmetry.
Smf115 (talk) 00:39, 17 May 2018 (BST)Clear tabulation of the charges and good mention of the symmetry and electronegativities to analyse the charge differences.
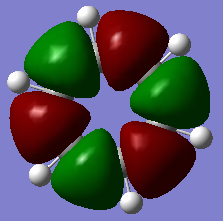
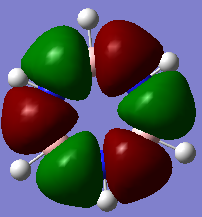
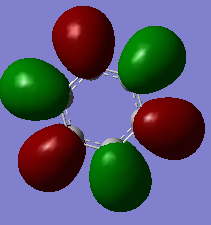
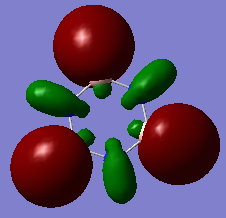
Molecular Orbitals of Benzene and Borazine
| Benzene | Borazine | Discussion |
|---|---|---|
 |
 |
These orbitals are very similar for both benzene and borazine. It is formed from p orbitals parallel to the ring on each carbon in benzene and on each boron and nitrogen in borazine. The orbitals are arranged alternating polarities so that there is overlap of the same phase between each atom in both borazine and benzene. |
 |
 |
these orbitals are formed from the p orbital on each atom in the ring that is facing out towards the hydrogen atom in combination with the s orbital from the hydrogen atom. In both molecules the s orbitals are alternating phases. In benzene the p orbitals are arranged so that the phases match with the h atoms. In borazine the p orbitals are all arranged with the same phases meaning where there is matching with the h 1s orbital the molecular orbital is made larger and where they do not match the molecular orbital is much smaller. |
 |
 |
These molecular orbitals are formed from p orbitals on the ring atoms and p orbitals on the hydrogen atoms all perpendicular to the ring. On each side of benzene 3 carbon p orbitals are orientated in each direction and therefore overlap and there is also bonding of the same phase with 2 h atoms. In borazine only 2 carbons p orbitals are in the same phase on each side and 1 h atom has orbitals that the phases on each side. |
Smf115 (talk) 00:13, 17 May 2018 (BST)Nice range of MOs, however, it hasn't been labelled which ones they are. Consider some of the key terminology such as sigma- or pi-, bonding and antibonding, when comparing the MOs as the discussion doesn't cover a lot of the necessary points. The AO contributions aren't quite correct but a good attmept has been made to recognise them.
Aromaticity
The common view of aromaticity is the non-bonded p orbitals in benzene overlapping to form rings of electron density above and below the carbon ring. For benzene there is a molecular orbital that closely resembles this idea however there are so many more molecular orbitals are not at all seen in this simple model of benzene. Any aromatic compound must follow Huckel's rule of having 4n+2 π electrons. This means that borazine is also considered aromatic. In borazine each atom on the ring does not have 1 partially filled p orbital and therefore the simple view for benzene no longer holds for all aromatic compounds. In borazine there is a lone pair on nitrogen atoms and an empty p orbital on each boron. It could be assumed that each nitrogen donates one electron to a boron and therefore the same system would exist as that in benzene however it can be seen from the molecular orbital and charge density analysis performed that this is not true. Nitrogen holds a partial negative charge and therefore holds on to electrons stronger and would not likely donate one to boron.
The calculated molecular orbitals of both compounds consist of many different bonding and antibonding π orbital combinations which are filled. This shows that there is significantly more going on within the molecule that simply all π orbitals overlapping to form 2 nice rings. For example the orbitals pictured last above. These orbitals are an example of the existence of antibonding character within the p orbital rings. It shows that the ring formation depends entirely on the phase orientation of each and every p orbital around the ring. The simple view or aromaticity assumes that these orbitals are all in line and therefore is not an accurate description of what aromaticity is.
Smf115 (talk) 00:11, 17 May 2018 (BST)Good description of the key concepts of aromaticity. Good ideas but they aren't quite correct, for example ring formation doesn't rely entirely on phase orientation and mention of further points, such as sigma-aromaticity, would be good to see.
Smf115 (talk) 00:42, 17 May 2018 (BST)A good attempt overall, however, some key information and ideas are missing throughout.
References
[1] P. Hunt, Lecture 4 Tutorial Problem Model Answers, from http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf accessed on 23/5/18.