Rep:Mod:rjw36

Transition states are defined as the critical configuration, at the highest point of the most favorable reaction pathway on a potential energy surface. Characterizing these critical states is important when understanding the mechanism of a reaction. However due to their transitory existence, it is not possible to make experimental measurements on their structure. Estimations can be made by considering Hammond's postulate and using computational methods to calculate activation energy. Previous studies have done this by using a fitted formula involving an analytical function of atomic coordinates, however this proves insufficient for larger molecules.


The transition states for the Cope re-arrangement and Diels Alder reaction were studied using a different, molecular orbital based method. This involved running optimizations at different levels of theory (HF/3-21G and B3LYP/6-31G*) , solving the Schrodinger Equation and locating transition structures from the local shape of each potential energy surface. From this the preferred reaction mechanism was determined and favored transition state for both reactions. Overall a conclusion was drawn as to which level of theory provided the most accurate data set giving values near to any experimental measurements.

Cope Rearrangement

Figure 1: Cope Re-arrangement of 1,5 hexadiene

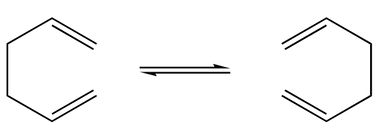
The Cope Re-arrangement is [3,3] sigma tropic shift of 1,5 dienes that occurs in a pericyclic fashion. Named solely after its inventor Arthur Cope , 1,5 hexadiene re-arranges in a thermally driven reaction yielding a product isoenergetic to its reactant. The reaction is believed to occur via a 'concerted' mechanism that passes through a transition state resembling either a 'chair' or 'boat' structure. Previous research concludes that the boat conformer lies significantly higher in energy, however the exact transition state in undefined. 1,5 hexadiene has possible 'anti' and 'gauche' stereoisomers because of the free rotation around the sp3 hybridized skeletal carbons. The different conformers will be investigated, along with the low energy minima and transition state structures to give a better understanding of the preferred mechanism.

Nf710 (talk) 15:28, 20 January 2016 (UTC) good knowledge of the mechanistics behind the reaction, you could have shown more knowledge of the computational methods

Chair Transition State	Boat Transition State

1,5 Hexadiene Conformers


A total of 8 energetically different conformers were possible and 2 of each linkage were investigated. Each conformer was optimized to compute energy values and associate symmetry point groups.


The first structure drawn was an anti conformer that had a dihedral angle of 180°. It was 'cleaned' using the clean function and optimized using the HF/ 3-21G basis set. It had an energy value of -231.692601805 a.u, and a C2 symmetry point group. 
This structure was identified specifically as the ‘’Anti 1’’ conformer on comparison to Appendix 1 Reference [3].

Anti 1			Structure
File Name	Attempt Anti1		Anti 1
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69260235	a.u
RMS Gradient Norm	0.00001824	a.u
Imaginary Freq
Dipole Moment	0.2021	debye
Point Group	C2





Anti 1 log file.

The second molecule drawn had the opposing 'gauche' linkage giving rise to a dihedral angle of 68°. The same HF/3-21G optimization conditions were applied yielding a structure with an energy of -231.69266 a.u and a point group of C1. This was identified as the ‘Gauche 3’ conformer.

Gauche 3			Structure
File Name	react_gauche3		Gauche 3
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.69266120	a.u
RMS Gradient Norm	0.00001176	a.u
Imaginary Freq
Dipole Moment	0.3406	debye
Point Group	C1

Gauche3 log file.

Energy Analysis

Figure 2: MO diagram showing HOMO of gauche 3 conformer.

Drawing Newman projections of 1,5 hexadiene would suggest that one of the anti conformers would be the lowest energy structure. In this conformer the bulky alkene groups are anti-periplanar to one another, with a dihedral angle of 180°, so any steric interaction is minimized.

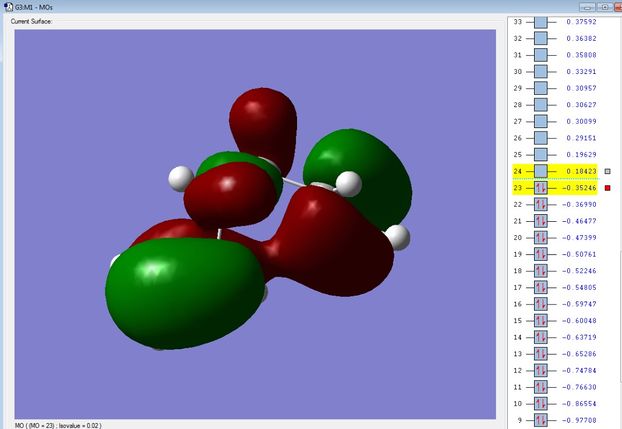
However, the optimized structures show it is the 'Gauche 3' conformer that is the lowest in energy. Inspection of the molecular orbitals show a favourable bonding interaction exists between the π orbitals of each terminal alkene, seen in Figure 2. This gives a strong stabilizing effect and lowers the overall energy of the molecule.

Nf710 (talk) 15:32, 20 January 2016 (UTC) Good use of the MOs to explain the ordering

Comparison of energy theory levels using Anti 1,5 Hexadiene conformer

The ‘anti 2’ conformer was optimized to two different levels of theory. The first optimization was run at the HF/3-21G level, whilst the second optimization was carried out at the more advanced B3LYP/6-31G* (6-31G(d)) level. As expected the use of different theory levels yielded optimized structures with different energies. However the point group in both optimizations remained unchanged.

Nf710 (talk) 15:34, 20 January 2016 (UTC)IT MAKES NO SENSE TO COMPARE DIFFERENT LEVELS OF THEOREY. They have different terms in the hamaltonian so it is meaningless

The change in geometry was measured by comparing the carbon-carbon bond lengths and dihedral angles. Minimal changes were visible in C2-C3 and C3-C4 bond lengths, however the greatest change was in C1-C2 length. The more advanced optimization showed an increased alkene bond length closer in proximity to the average literature length of 1.33 Å. But with the largest difference being 0.2 Å, it can be concluded changing the theory level does not significantly impact the geometry of the anti 2 conformer. Both basis sets will yield similar results for geometry calculations, with the only influencing factor being the running cost of each. A lower level basis set can be run at a lower cost.

Anti 2			Structure
File Name	attempt1_Anti2_		Anti 2 3-21G
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Charge	0
Spin	Singlet
Total Energy	-231.692535279	a.u
RMS Gradient Norm	0.00001891	a.u
Imaginary Freq
Dipole Moment	0.0000	debye
Point Group	Ci

Anti 2 3-21G log file.

Anti 2			Structure
File Name	Anti2_optimisation6-31G(d)		Anti 2 6-31G*
File Type	.chk
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	6-31G(d)
Charge	0
Spin	Singlet
Total Energy	-234.61171063	a.u
RMS Gradient Norm	0.00001249	a.u
Imaginary Freq
Dipole Moment	0.0000	debye
Point Group	Ci

Anti 2 6-31G* log file.

	Bond Lengths (A)			Dihedral Angle (°)
	C1-C2	C2-C3	C3-C4	C1-C2-C3-C4	C2-C3-C4-C5
HF/3-21G	1.31613	1.50891	1.55275	-114.669	180.000
B3LYP/6-31G*	1.33350	1.50419	1.54816	-118.600	180.000

Frequency Analysis

Figure 3: IR Spectrum of Anti 2 conformer showing

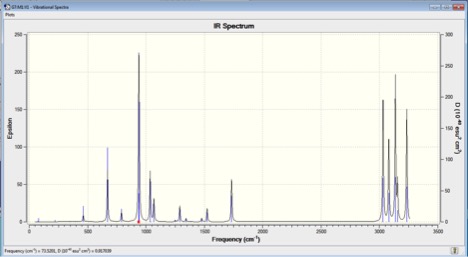
A Frequency analysis was carried out to confirm that all the optimizations had run to a minimum. This would allow computed energy values to be compared to measured experimental data. The frequency calculations showed all positive vibrations, with the absence of any imaginary frequencies. Had the reaction not gone to a minimum imaginary values would have been detected and shown in the IR spectrum, Figure 3. The spectrum depicts an expected C-C bond stretch at 2900 cm^-1.

The Thermochemical data extracted from the frequency calculation gives a more detailed account of potential energies. A range of enthalpies and energy values were found at 0K, 298.15 K and 1 atm. In the sum of electronic and thermal energies translational, rotational and vibrational contributions were expected, however at 0K the zero point energy is made up of the vibrational residue within the molecule. The Enthalpy and Free energy values both have corrective terms added to them. The 'RT' term is added to the enthalpy (H = E + RT) whereas a entropic term is added to the free energy value (G= H -TS).

Nf710 (talk) 15:41, 20 January 2016 (UTC) Very in detailed freqiency analysis but we generally only do this so that we can she that it is not at a transition state, checking there are no imaginaries

Mode	Frequency (cm-1)	Infared	Thermochemistry
1	73.52	0.0169	Sum of electronic and zero-point Energies	-234.469219
2	80.53	0.1204
3	121.00	0.0000
4	220.28	0.1577	Sum of electronic and thermal Energies	-234.461869
5	348.90	0.0000
6	394.63	0.0000
7	462.23	2.9021	Sum of electronic and thermal Enthalpies	-234.460925
8	625.75	0.0000
9	669.43	19.9859
10	778.30	4.0616	Sum of electronic and thermal Free Energies	-234.500809
11	938.37	10.8004
12	938.51	0.0000

Animation of Mode 1

Anti 2 6-31G* Frequency analysis log file.

Optimizing ‘Chair’ and 'Boat' conformers

The chair transition state was investigated first. An allyl fragment (C₂H₅) was drawn and optimized at the HT/3-21G level. The optimized structured was copied and pasted across and the 2 new fragments orientated to resemble a rough example of the chair transition state. The molecule was symmetrized and the terminal alkene ends set apart 2.2 Å.

The chair transition state was optimized by 2 different methods:

1.) Computing Force Constants

2.) Frozen co-ordinate method

Computing Force Constants

In this method the force constants were computed by calculating a force constant matrix (Hessian) that was continually updated on optimzation. This method was possible because we had a guess idea that the transition state of the Cope Re-arrangement near resembled a chair structure.

The chair conformer was optimized to a transition state via the TS(Berny) Job Type with the force constants set to be calculated once and the ‘Opt=NoEigen’ keywords added to stop the programme crashing.

The frequency calculation showed one imaginary vibrational mode at 818 cm^-1 confirming a transition state had been found. This mode was imaginary because the acting force and displacement of the molecule were in opposite directions. Using the relationship between frequency and force constant (k), from the Quantum Harmonic Oscillator, a negative k value would give an imaginary frequency.

$\overline{\nu }=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu }}$

The vibration mode showed an animation corresponding to to the Cope Rearrangement. 


Chair Structure			Structure	Frequency (cm-1)
File Name	Chair_Opt_Method1		Chair TS	-818.01
File Type	.log			209.70
Calculation Type	FREQ			396.07
Calculation Method	RHF			419.22
Basis Set	3-21G			422.21
Charge	0			497.28
Spin	Singlet			528.26
Total Energy	-231.61932230	a.u		574.97
RMS Gradient Norm	0.00003004	a.u		876.18
Imaginary Freq	1			876.71
Dipole Moment	0.0000	Debye		905.21
Point Group	C2h			909.68

Mode 1: Animation of Cope Re-arrangement Chair TS M1

Chair Optimization Method 1 Log File.

Frozen Co-ordinate Method

The Frozen Co-ordinate Method involved freezing the 2 terminal carbons on each allyl fragment using the Reductant Coordinator Editor. The frozen structure was optimized to a transition state at the HF/3-21G level of theory and the optimized product had terminal bonds still at a length of 2.2 Å. These bonds were optimized to a transition state in the second optimization, and a simultaneous frequency calculation was run. Similarly a single imaginary frequency was detected at roughly 818 cm^-1 with an animation confirming the Cope re-arrangment.

Chair Structure			Structure	Frequency (cm-1)
File Name	Attempt1_chairopt_freeze		Chair TS	-817.89
File Type	.log			209.63
Calculation Type	FREQ			395.89
Calculation Method	RHF			419.16
Basis Set	3-21G			421.94
Charge	0			527.94
Spin	Singlet			574.70
Total Energy	-231.61518514	a.u		876.18
RMS Gradient Norm	0.00325807	a.u		876.61
Imaginary Freq	1			905.27
Dipole Moment	0.0000	debye		909.62
Point Group	C2h			1019.08

Mode 1: Animation of Cope Re-arrangement Chair TS M2

Chair Optimization Method 2 Log File.

QST2 Method

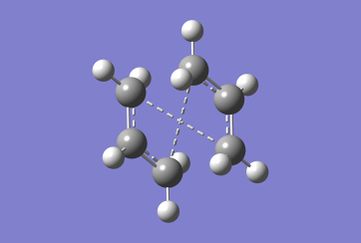
The boat transition state was optimized using the QST2 method, whereby transition state calculations were carried out by interpolating between the reactants and products. These were drawn in separate windows of GaussView by duplicating optimized Ci conformers of 1,5-hexadiene (Anti 2). The atoms on the reactant and product were re-orientated to appear as mirror images and 
the atoms on the product molecule were renumbered as to match outcome of the Cope Re-arrangement (Figure 4).

This structure was optimized to a transition state using TS(QST2) method to the HF/3-21G level of theory. The angles of the structure did not resemble that of a typical boat conformation and the job submitted failed as expected. The molecule appears mismatched with overlapping bonds because it has translated across during bond formation (Figure 5).

Figure 4

Figure 5

The dihedral angles were changed to 0° and the inside C-C-C angle for both C2-C3-C4 and C3-C4-C5 was made equal to 100°. This resembled a more 'boat' type structure. The transition state optimization was re-run and confirmed as successful by detected frequency at -839.90 cm^-1.

Boat Structure			Structure	Frequency (cm-1)
File Name	boat_attempt4_angles1		Boat TS	-839.90
File Type	.log			155.22
Calculation Type	FOPT			381.93
Calculation Method	RHF			395.21
Basis Set	3-21G			441.92
Charge	0			459.27
Spin	Singlet			459.83
Total Energy	-231.60280242	a.u		494.22
RMS Gradient Norm	0.00001962	a.u		858.44
Imaginary Freq	1			865.37
Dipole Moment	0.1583	debye		872.11
Point Group	C			886.06





Mode 1: Cope Re-arrangement Boat TS

Boat Optimization QST2 Log File.

IRC and Activation Energies

It is not possible to predict from the boat and chair transition states the exact conformer of the product. But the IRC tool in Gaussian View allows the minimum energy path to be followed on a potential energy surface. This path runs from the transition state down to the local minima, which can be assigned by comparing its energy values with the known energy of each conformer.

Figure 6: IRC of Chair TS- Optimized by Method 2

An IRC was run on the chair transition state. The reaction co-ordinate was computed in a single direction because of its know symmetry -if this were not the case then the calculations would be run in both directions. The force constant was selected as being calculated always and the number of points set to 50.

The IRC showed 44 intermediate geometries from the reaction, but on inspection these did not appear to have reached a minimum. This was achieved by taking the 44th intermediate and running a standard HF/3-21G minimum optimization. This was not the only way to achieved the minimum however it was the fastest approach. The only limitation with this being that if the minimum wasn't close enough to the local minima, it could give the wrong conformer. The optimized conformer was identified as Gauche 2 from its energy value (-231.6166700 a.u.).

The activation energies of both transition states were calculated and compared at the HF/3-21G and BLYP/6-31G* level of theory. This involved re-optimizing previous formed chair and boat structures to the higher theory level and performing simultaneous frequency calculations. The thermodynamic data was used to calculate activation energies using the conversion rate 1 Hartree = 627.509 kcal/mol. As predicted the Boat TS had a higher energy barrier compared to the Chair due to the slight angle strain of the skeletal carbons. The activation energy data at 0K shows that the more advanced theory gives values closer to or within the experimental range. The lower basis set appears to be less accurate when calculating activation energies. Therefore it can be concluded that when performing energy calculations, the B3LYP/6-31G* is the better basis set to use and gives a more realistic picture of the molecules electron density. More selection is required when deciding on a level of theory for energy compared to geometry.

IRC Animation	Optimized Minimum Structure
	Gauche 2 Conformer

Gauche 2 Log File.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466705	-231.461345	-234.556931	-234.414908	-234.408980
Boat TS	-231.602802	-231.450928	-231.445299	-234.543079	-234.402356	-234.396012
Reactant (anti2)	-231.692710	-231.539539	-231.532565	-234.611711	-234.469219	-234.461869

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	34.08	33.19	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.33	44.7 ± 2.0

Chair 6-31G* Optimization Log File.

Boat 6-31G* Optimization Log File.

Nf710 (talk) 15:48, 20 January 2016 (UTC) Your energies are correct This was a good report however you could have shown more understanding of the underlying methods

Diels Alder Reaction

Figure 7: Diels Alder forming Cyclohexadiene

Figure 8: Diels Alder reaction of 1,3 cyclohexadiene and Maleic Anhydride

(Small typo in Fig 7. Please reference any images that you haven't made Tam10 (talk) 15:09, 11 January 2016 (UTC))

Diels Alder is a type of pericyclic [4+2] cycloaddition resulting in the formation of 2 new carbon-carbon σ bonds. The reaction involves the conjugated π system of a diene interacting with the π orbitals of a dienophile in a concerted manor. In most cases the dienophile is a substituted alkene with bonding electron donating or electron withdrawing R groups. The electronic character of the R groups and approaching trajectory of the reactants are two factors that influence the regio and stereo selectivity of this pericyclic reaction . The Woodward Hoffman rules can be applied to gain a better understanding and identify a reaction as allowed or forbidden. This will depend on the orbital overlap between the HOMO and LUMO. Allowed reactions take place when there is a low energy barrier, and forbidden reactions when there is a high energy barrier. Specifically forbidden reactions take place when the orbitals have different symmetry properties but there is no significant orbital overlap. Although they are unlikely to occur, they can still take place if there is a large energy input into the system.

The simplest example of a [4+2] cycloaddition is the reaction of 1,3-butadiene with ethylene. The 4π electrons from 1,3 butadiene interact with the 2π electrons from ethylene. The computed calculations run on this reaction will confirm that the principal interactions involve the π/ π* orbitals of ethylene and the HOMO/LUMO of butadiene, and prove that the HOMO of ethylene and the LUMO of butadiene are both symmetric whereas the the LUMO of ethylene and the HOMO of butadiene are antisymmetric. This is an example of a prototypical reaction but has limited information about the formation of exo and endo products.

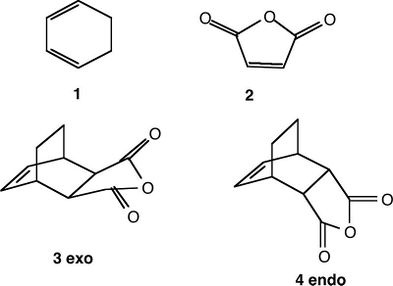
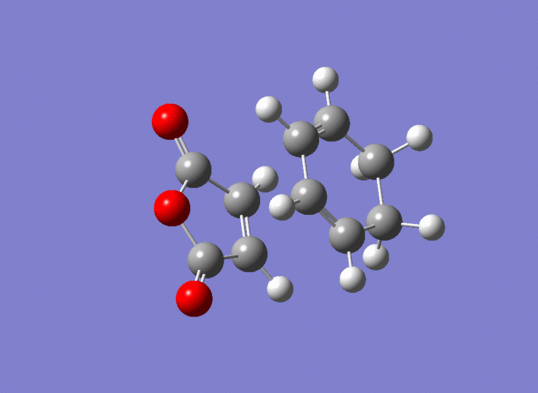
A study was conducted on a second Diels Alder between 1,3 cyclohexadiene (1) and Maleic Anhydride (2). This has the possibility of forming 2 distinct stereoisomer products- 3-exo and 4-endo. 'Endo' and 'Exo' describe the orientation of the substituents on the dienophile as it approaches the diene. In the exo orientation the substituents are facing upwards towards the diene whereas in the endo orientation the substituents are facing downwards and can interact with the conjugated π system in 1,3 cyclohexadiene. The favoured stereoisomer will depend on the energy of the transition state. The endo rule states that the endo product is usually the major isomer due to favouring secondary orbital interactions. Computed methods were used to compare the different transition states on this reaction pathway and investigate which product is favoured. The methods used for both these reactions are based on quantum mechanics.

Cis-butadiene and Ethylene HOMO and LUMO's

Cis-Butadiene was optimised to a minimum at the Semi-Emperical AM1 level of theory and the HOMO and LUMO Molecular Orbitals were depicted. It was found with respect to the reaction plane the HOMO was antisymmetric (a) and the LUMO was symmetric (s).

HOMO	LUMO

Butadiene Opt Log File.

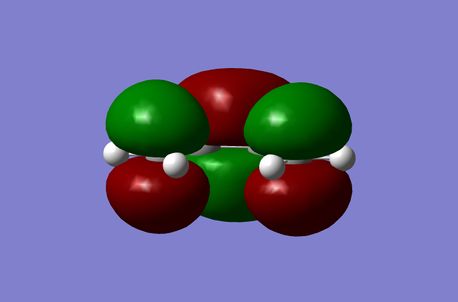
Simiilarly ethylene was optimised to a minimum at the Semi-Emperical AM1 level of theory with the opposite outcome. The HOMO was symmetric whereas the LUMO appeared antisymmetric.

HOMO	LUMO

Ethene Opt Log File.

Transition State- cis-Butadiene and Ethylene

Figure 8: Proposed Transition State of ethylene and 1,3-butadiene {4+2} cyclcoaddition

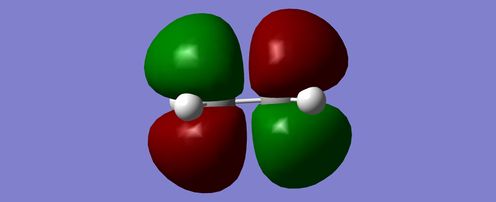
The transition state will be made up of a combination of the molecular orbitals above. If the overlap is from the:

Pair 1- HOMO from butadiene and LUMO from ethene

Pair 2- HOMO from ethene and the LUMO from cis-butadiene

Pair 1 is the normal electron demand reaction and is the favoured case for most Diels Alder reactions, whereas Pair 2 is the inverse electron demand. The HOMO and LUMO of the transition state will be either pair 1 or pair 2.

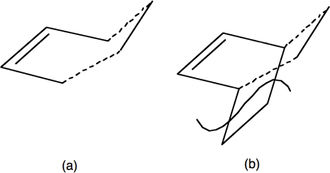
The transition state was optimized using the 'Computed Force Constant' method. Based on previous research, it was predicted to be an envelope structure a, which maximizes orbital overlap between the π orbitals in ethene and the π system in butadiene. The structure was build in Gaussian View by drawing structure b (Figure 8) and removing the lower CH₂-CH₂ fragment. The dashed inter-fragment distances were set to a distance of 2.2 Å. and the structure optimized to a transition state at the Semi-Emperical AM1 level of theory and frequency calculation run. Force constants were calculated once.

The optimization shows a transition structure which resembles structure a. The partially formed double bond between C2-C3 on cis-butadiene appears with a bond length of 1.39747 Å. This is inbetween the standard sp² and sp³ hybridized carbon-carbon bond lengths, 1.33 Å and 1.54 Å respectively. The other partially formed bonds in the transition state are the σ carbon-carbon bond between the 2 reactants. The computed structure measures these carbons with a distance of is 2.1 Å, deviating slightly from the set distance of 2.2 Å. At this length it is concluded that there is a high probability of orbital overlap between the 2 carbons. From the carbon Van de Waals radius, 170 pm, it can be assumed that any 2 carbon atoms with a separation distance lower than 2.4 Å will show some kind of orbital interaction.

Frequency Results show a single imaginary frequency at -956.29 cm^-1 corresponding to the formation of two new σ bonds. Seen from the simulation, the bond formation is synchronous and is the only vibrational frequency illustrating the approach trajectory of the 2 reactants. The second lowest frequency corresponds to the rotation of ethene around its central axis.

Envelope Structure			Structure	Frequency (cm-1)
File Name	ENVELOPE TS OPT		Envelope TS	-956.29
File Type	.log			147.20
Calculation Type	FREQ			246.63
Calculation Method	RAM1			272.41
Basis Set	ZDO			389.68
Charge	0			422.10
Spin	Singlet			505.97
Total Energy	0.11165465	a.u		629.65
RMS Gradient Norm	0.00001072	a.u		685.48
Imaginary Freq	1			729.50
Dipole Moment	0.5606	debye		816.76
Point Group	C1			876.38

Mode 1: Confirming Transition State optimization.

Envelope TS Opt Log File.

IRC and Product Minimization

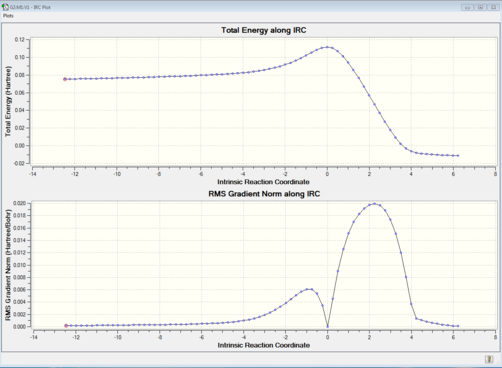
Further IRC calculations were run to confirm the correct transitition state had formed and the minimum on the reaction profile corresponded to cyclohexene. The IRC was run in both directions whilst set to compute a force constant throughout. The level of theory was kept the same as the previous optimization (SE AM1) and the plotted results shows a successful anti-symmetric reaction profile with a distinct difference in energy levels between the reactants and the products. An animation of the IRC illustrates the correct Diels Alder reaction is taking place. A minimum optimization was run on the IRC product to confirm it was cyclohexene.

Figure 9: IRC showing the Diels Alder reaction between cis-butadiene and ethylene

IRC Animation	Optimized Minimum Structure
	Cyclohexene

IRC Minimum Opt. Log File.

Transition State MO Analysis

The HOMO of the transition state is antisymmetric and corresponds to Pair 1- HOMO from butadiene and LUMO from ethene.

This confirms that this reaction is an example of a Normal Electron Demand Diels Alder and that Pair 1 has the lowest energy difference between the HOMO and LUMO. These orbitals will interact in the favoured reaction pathway. The LUMO of the transition state is antisymmetric and corresponds to Pair 2.

HOMO	LUMO

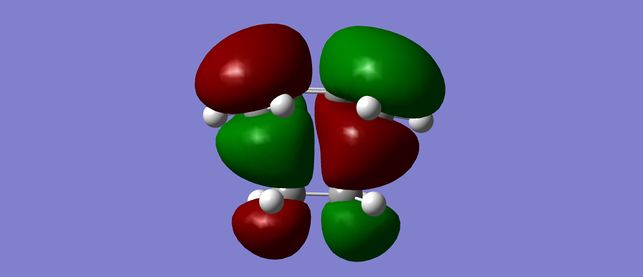
Diels Alder Regioselectivity

Regio-selectivity was investigated in the reaction between 1,3-cyclohexadiene and maleic anhydride forming exo and endo products.

On drawing the transition states the previous Diels Alder envelope structure was used as a template. It was modified by addition of a CH₂-CH₂ and a maleic anhydride group. Optimizations and simultaneous frequency calculations were run on both structures at the Semi-Emperical AM1 level of theory. Only one level of theory was used to enable an accurate comparison between the two transition states.

3-Exo Structure

The exo structure was confirmed as a transition state on analysis of the relative frequencies and the simulation of mode 1 shows a Diels Alder reaction. The summary information is given below. The Jmol file confirms the state is exo because the maleic group appears to be facing upwards towards the diene whereas the corresponding 2 hydrogens have a downwards orientation.

3 Exo TS			Structure	Frequencies
				Mode	Vibration (cm-1)
File Name	3 Exo TS Opt		3 exo	1	-812.21
File Type	log.			2	60.87
Calculation Type	FREQ			3	123.87
Calculation Method	RAM1			4	139.21
Basis Set	ZDO			5	167.50
Charge	0			6	218.92
Spin	Singlet			7	234.76
E(RAM1)	-0.05041985	a.u		8	257.83
RMS Gradient Norm	0.00000305	a.u		9	359.45
Imaginary Freq	1			10	390.63
Dipole Moment	5.5640	debye		11	446.60
Point Group	C1			12	500.83

3 Exo TS Mode 1 Simulation

Exo TS Opt Log File.

4-Endo Structure

The endo transition structure was confirmed by a similar analysis. The imaginary frequency at -806.38 shows a cycloaddition reaction and the summary information appears different to the exo structure, confirming a different transition state. Looking at the structure there is a clear visible difference between the two transition states, the maleic group appears to be pointing downwards, away from the 1,3 conjugated π system of 1,3-cyclohexadiene and hence this is the endo transition state.

Although both structures have been identified as transition states IRC calculations need to be run to ensure they both correspond to the same product. This will also provide more information into the differences between the exo and endo reaction pathways.

4 Endo TS			Structure	Frequencies
				Mode	Vibration (cm-1)
File Name	4 Endo TS Opt		4 endo	1	-806.38
File Type	log.			2	62.43
Calculation Type	FREQ			3	111.74
Calculation Method	RAM1			4	113.60
Basis Set	ZDO			5	166.38
Charge	0			6	188.07
Spin	Singlet			7	221.77
E(RAM1)	-0.05150480	a.u		8	241.44
RMS Gradient Norm	0.00000652	a.u		9	340.34
Imaginary Freq	1			10	392.29
Dipole Moment	6.1661	debye		11	447.54
Point Group	C1			12	492.38

4 Endo TS Mode 1 Simulation

Endo TS Opt Log File.

Comparison of Endo and Exo States

(I can't find any mention of steric effects or a comparison of the geometry Tam10 (talk) 15:09, 11 January 2016 (UTC))

IRC

IRC's were run in both directions on the endo and exo transition states. It was intially set to use 20 points along the reaction profile, however the graph produced didn't appear to reach to a minimum. This was then increased to 50 points and the 'Recorrect Steps' set to Never to avoid the calculation crashing. The profiles produced appear as mirror images of each other. The reaction profile shows both reaching a maximum at around 0 and a clear energy barrier between the reactants and product. Looking at the animations of both IRC's explains their differences. The animation for the 3 exo shows the reaction profile produced is in the reverse direction, i.e the bicyclic product dissociating to its reactants, whereas the endo reaction profile is in the forward direction. However they both show the same Diels Alder reaction and the formation of the same carbon-carbon σ bonds.

The energy values of both endo and exo products were calculated in the IRC. The endo product appeared lower in energy at -0.15927 a.u compared to the exo product at -0.158531 a.u. Although the difference in energies is small this shows that the endo product is the most stable in energy, namely the thermodynamic product.

3-Exo IRC	4-Endo IRC

3-Exo IRC Log File.

4-Endo IRC Log File.

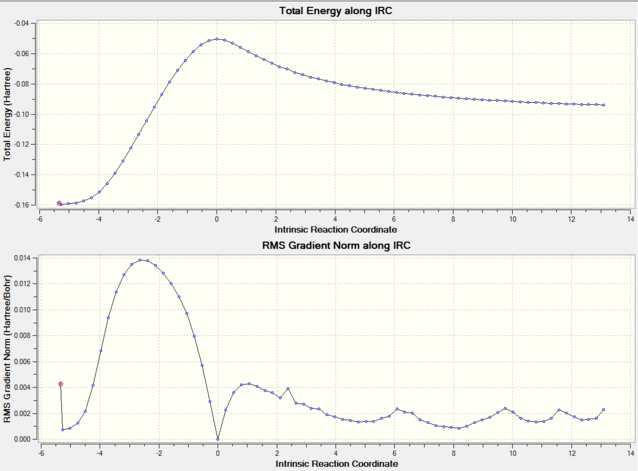
HOMO's

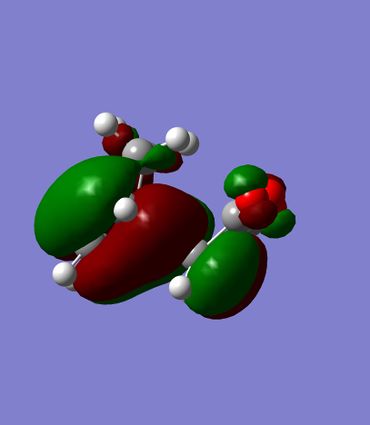
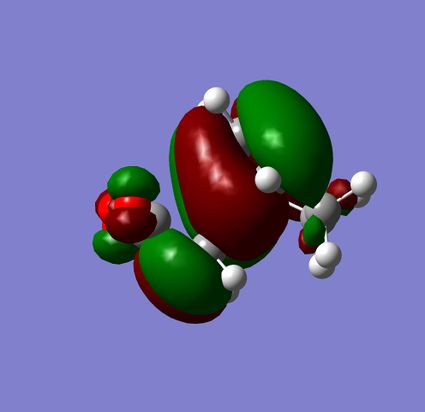
The HOMO's of both transition states were visualized. They show very similar molecular orbital pictures which appear to be mirror images of one another. In both transition states there is an anitbonding interaction between the oxygen atoms of the maleic anhydride group and the its skeletal carbons. The nodes appear to be out of phase. As expected there is a large amount of density at the centre of the transition state where the new 2 new σ bonds are forming.

The HOMO shows little interaction between the (C=O)-O-(C=O)- fragment and the rest of the molecule. Zooming in further to the HOMO shows a small node corresponding to the p orbital of oxygen and larger nodes of C=O resembling a p orbital. The carbons making up the (C=O)-O-(C=O)- fragment appear only to interact with other carbons in the Maleic anhydride group. Therefore it can be concluded that looking at the HOMO of the transition state provides little informaiton into any possible stabalising effects present.

HOMO of 3-exo	HOMO of 4-endo
HOMO of 3-exo (C=O)-O-(C=O)- fragment	HOMO of 4-endo (C=O)-O-(C=O)- fragment

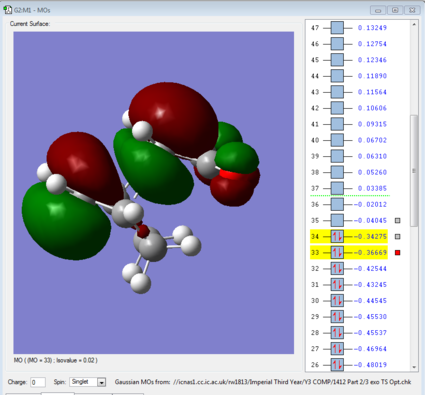
Secondary Orbital Effect

The secondary orbital effect was not visible in the HOMO's of both transition states, however further inspection showed it was visible in MO 33 (- 1 HOMO). Both transition states were orientated to the same viewpoint to enable an accurate comparison. In the 4 endo structure there is an in phase interaction between the oxygen atoms on the -C(=O)-C-C(=O) Maleic Anhydride fragment and carbons making up the 4π conjugated system. This has a stabilizing effect on the structure and hence is the reason why the endo product appeared lower in energy in the IRC. Although there appears to be some out of phase bonding between the carbonyl groups and the skeletal maleic anhydride fragment, this is counteracted by the stabilizing effect.

The exo product does not show any stabilizing secondary orbital overlap effects.

3-exo	4-endo

Activation Energies

The final comparison made between the exo and endo transition state was a comparison of their corresponding energies.

In order to calculate activation energies, the 2 reactants had to be drawn in Gaussian View and optimized to the same level as the transition state, Semi Emperical AM1. The electronic energies were calculated using the optimized log files taking into considering the zero point correction. The conversion rate of 1 Hatree = 627.509 kcal/mol was used.

The activation energy for the endo product is lower than the activation energy for the exo product, with the difference between the two being 0.68 kcal/ mol. This shows that the reaction pathway with the endo transition state is the favoured reaction route and has the lowest energy barrier. In this example the endo product is also the kinetic product of the Diels Alder reaction.

	Electronic Energy (Hatrees)	Electronic Energy (kcal/ mol)	Activation Energy (kcal/ mol)
Maleic Anhydride	- 0.121764	- 76.408080
1,3 Cyclohexadiene	0.027712	17.389546
Total Reactants	- 0.094052	-59.018534
3 exo	-0.050419	- 31.6384069	27.38
4 endo	- 0.051505	- 32.319882	26.70

Conclusion

In Conclusion, the 2 different examples of pericyclic reactions have been successfully evaluated using computational calculations giving results close to experimental data. This confirms that although computational methods use approximations, they are a good reflection of the true nature of a reaction. The Cope Re-arrangement confirmed that for geometry calculations there is no basis set preference, however for energy calculations a more advanced basis set gives a more accurate theoretical result. It was found using 6 Molecular orbitals better reflects the 'mould' of electron density and following the Arrhenius equation, the greater the temperature the lower the activation energy.

In terms of activation energies, the results show that the Chair TS was the lowest in energy and hence the kinetically favored reaction pathway for the Cope Re-arrangement. Whereas in the Diels Alder reaction the kinetic and thermodynamic product were both identified to follow the reaction pathway with the endo transition state. This confirmed the hypothesis to be correct.

Further computational studies could be conducted on the Diels Alder reaction using a different level of theory. This would enable a greater understanding in the basis level that best represents the reaction. This has already been identified for the Cope Re-arrangment as 6-31G* basis set.