Rep:Mod:rebeccalee3
Cope Rearrangement - 1,5-Hexadiene
Introduction
The cope rearrangement is also known as a [3,3]-sigmatropic shift. For a very long time, the mechanism was subject to a lot of controversy. Nowadays, its reaction is accepted to be a concerted one via the chair or boat transition state structure. The boat structure lies a bit above the chair in energy.
Past papers have shown that the B3LYP/6-31g(d) level of calculation has proven quite accurate in giving activation energies and enthalpies. The purpose of this part of the project is to calculate this for 1,5-hexadiene.
Initial Optimizations
1,5-hexadiene was drawn in gaussview as a linear chain with an anti linkage about the central four C atoms. The structure was cleaned to prepare for the calculations. For the first optimization, the app conformation was analyzed with a fixed 180.0° dihedral angle between the central four C atoms.
The optimization was run with the Hartree-Fock (HF) method with the 3-21G basis set. The initial settings of %mem=6MW in the Link 0 tab caused the last link of the calculation to abort. This was changed to 10MW in order to ensure that the calculation would run successfully.
The rest of the conformations were optimized using the same method and basis set as the initial optimization.
The table below shows the summary of each optimization (which was taken by opening the .chk file). When the point group was not indicated the molecule was edited with Edit --> Symmetrize. This was also used as a way to check the point group given in the summary table, as in most cases it reported C1, which is not the case for most of the molecules.
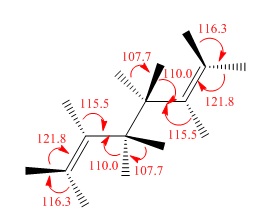
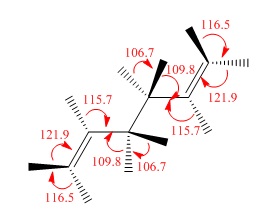
All app conformations had a fixed dihedral angle of 180.0°, and gauche had a fixed angle of 60.0°. The structures were changed by changing the angles of the terminal groups.
| Conformation | Structure | Point Group | Reference point group [1] | Energy HF/3-21G (a.u.) | Reference energy HF/3-21G(a.u.) [1] | Relative Energy (kcal/mol) | Summary & .log file of Optimization |
|---|---|---|---|---|---|---|---|
| Gauche 1 |  |
C2 | C2 | -231.68771613 | -231.68772 | 3.10 | 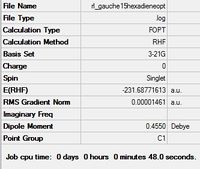
|
| Gauche 2 |  |
C2 | C2 | -231.69166702 | -231.69167 | 0.62 | 
|
| Gauche 3 |  |
C1 | C1 | -231.69266120 | -231.69266 | 0.00 | 
|
| Gauche 4 |  |
C2 | C2 | -231.69153032 | -231.69153 | 0.71 | 
|
| Gauche 5 |  |
C1 | C1 | -231.68961573 | -231.68962 | 1.91 | 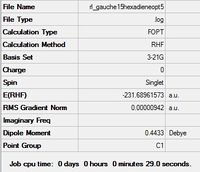
|
| Gauche 6 |  |
C1 | C1 | -231.68916016 | -231.68916 | 2.20 | 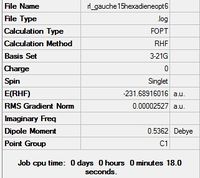
|
| App 1 |  |
C2 | C2 | -231.69260236 | -231.69260 | 0.04 | 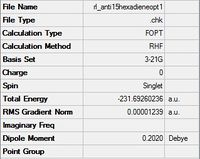
|
| App 2 |  |
Ci | Ci | -231.69253528 | -231.69254 | 0.08 | 
|
| App 3 |  |
C2h | C2h | -231.68907066 | -231.68907 | 2.25 | 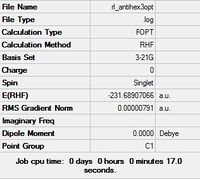
|
| App 4 |  |
C1 | C1 | -231.69097055 | -231.69097 | 1.06 | 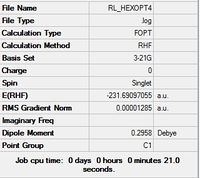
|
Gauche shows a large steric clash in comparison to the app conformation, and thus it can be guessed initially that the most stable conformation will be one of the app ones. In this case, the largest groups (vinyl) will be furthest away from each other, and due to this more favorable orientation the energy of the conformation should be more stable.
However, comparing all these structures above shows that the Gauche 3 conformer is the most stable. This contradicts the rationalization made earlier using sterics as the main factor. Thus it can be seen that there are other important factors that affect the stability of the conformations.
HF vs. DFT optimizations
It has been shown that the app 2 conformation is the reactant in this reaction. Since the HF optimization is not a very accurate method to use, the DFT method was used in order to increase the accuracy of the optimization of the molecule.
| Conformation | Structure | Point Group | Energy DFT B3LYP/6-31G(d) (a.u.) | Relative Energy (kcal/mol) | Summary & .log file of Optimization |
|---|---|---|---|---|---|
| App 2 | 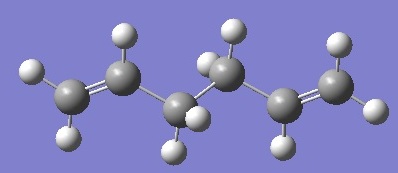 |
Ci | -231.61172164 | 50.79 | 
|
The energy from this method is a lot lower than that calculated for the HF optimization, however due to the different method and basis sets used these two results cannot actually be compared.
Job run time: HF/3-21G 21.0 sec., DFT B3LYP/6-31G(d) 2 min 28 sec.
Both optimizations give the same point group, however the bond lengths and angles do have a slight change. This shows that while the HF/3-21G optimization is not very accurate, it is still a pretty good calculation to use for estimations.
This also shows that it is helpful to first run a rough estimate of the structure in order to bring it down to the minimum, and then to further optimize it with a better method and basis set. This would also help reduce the time taken for the latter optimization.
Vibrational analysis
One use of the frequency analysis is that it gives an indication as to whether or not the optimization gave a minimum structure. This is shown in the .log file, in the "low frequencies" section.
The first line shows how accurate the optimization is, and the second line shows whether or not the given structure is a minimum. If there is a negative frequency in this line, it indicates that the structure is a maximum.
Low frequencies --- -5.6835 -2.3459 -2.0879 -0.0006 -0.0005 -0.0005 Low frequencies --- 71.1991 85.6862 116.1457
The information above corresponds to data from the .log file of the HF/3-21G optimization + frequency calculation.
Low frequencies --- -9.2070 -0.0012 -0.0010 -0.0006 4.0343 13.7709 Low frequencies --- 74.3306 81.0035 121.5399
The information above corresponds to the frequency calculation of the DFT B3LYP/6-31G(d) optimized structure. It shows good accuracy and that the structure is a minimum.
While both give a similar result in the frequency analysis, this is probably due to the small differences in their structures. However, it is best to use a better method and basis set wherever possible.
Thermochemistry analysis
Sum of electronic and zero-point Energies= -234.469205 Sum of electronic and thermal Energies= -234.461859 Sum of electronic and thermal Enthalpies= -234.460915 Sum of electronic and thermal Free Energies= -234.500779
The data above gives energy information taken at 298.15 K.
The first gives information on the potential energy when at 0 K + the zero-point vibrational energy: E = Eelec + ZPE. The second gives information on the energy when at 298.15 K and 1 atm pressure, including translational, rotational, and vibrational energy contributions at these conditions: E = E + Evib + Erot + Etrans. The third gives information on the correction for RT (particularly important for dissociation reactions): H = E + RT The fourth gives information on the energy, including the entropic contribution: G = H - TS.
Optimizing the chair transition structure
There is more than one method of optimizing transition states (TS): 1) computing force constants at the beginning of the calculation, 2) using the redundant coordinate editor, and 3) using QST2.
Method 2 was not run because the method would not work as described.
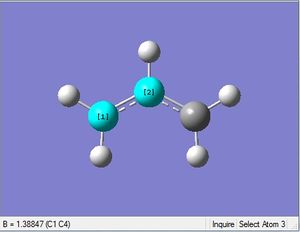
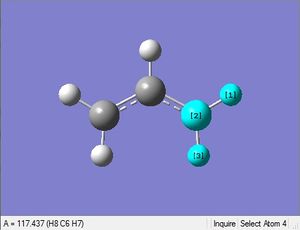
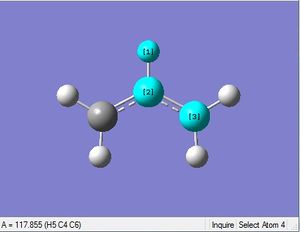
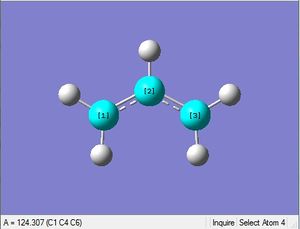
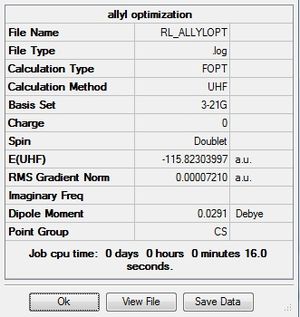
First an allyl fragment was optimized with the HF method and 3-21G basis set.
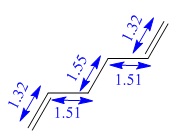
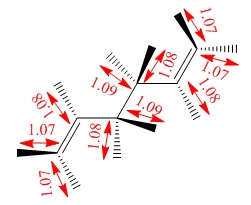
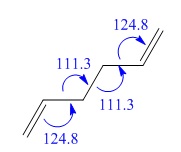
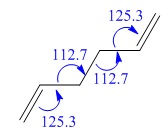
| C-H length | C-C length | H-C-H angle | H-C-C angle | C-C-C angle | Summary & .log file |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
|
| 1.07Å | 1.39Å | 117.4° | 117.9° | 124.3° | .log file |
This optimized fragment was then used to create a rough estimate of the chair TS. All of the following calculations used the HF method and 3-21G basis set.
Method 1
The Opt+Freq job was selected with optimization to a TS (Berny). The force constants were chosen to calculate once, with Opt=NoEigen as an additional keyword. This keyword helps prevent the calculation crashing if more than one imaginary frequency is detected during the job. This often happens if the guessed structure isn't close enough to the actual structure of the TS.
| C-C distance | Summary & .log file | Animation |
|---|---|---|
 |
 |
Vibration animation |
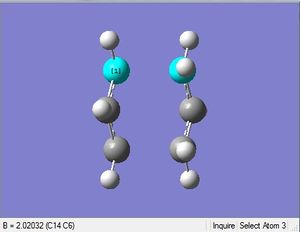
| 2.02 Å | .log file |
The imaginary frequency is -818 cm-1. The above vibration animation shows that it undergoes the Cope rearrangement.
IRC method
This method allows the minimum energy path to be followed from a given TS, down to its local minimum on the potential energy surface.
The job type chosen is IRC, with the forward direction selected as the molecule is symmetrical. The force constants are chosen to be calculated always with the number of points along the IRC changed to 25.
| Structure of first step | Structure of last step | RMS gradient | Energy path | Summary & .log file |
|---|---|---|---|---|
 |
 |
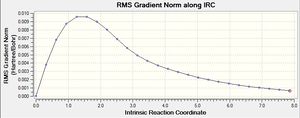 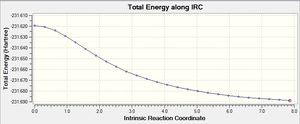 |
 .log file .log file
|
The .chk files shows that the minimum geometry hasn't been found yet. This leaves three options: 1) run a normal optimization on the last point 2) restart the IRC with a larger number of points, and 3) redo the IRC specifying that the force constant must be calculated at every step.
The second method was attempted, with all the same settings except for the number of points along the IRC was changed to 50.
| Structure of first step | Structure of last step | RMS gradient | Energy path | Summary & .log file |
|---|---|---|---|---|
 |
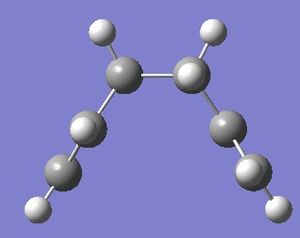 |
 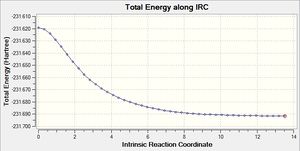 |
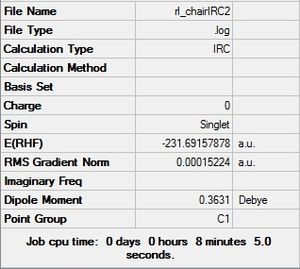 .log file .log file
|
Next, the first method was attempted using the normal optimization settings.
| Structure | Summary & .log file |
|---|---|
 |
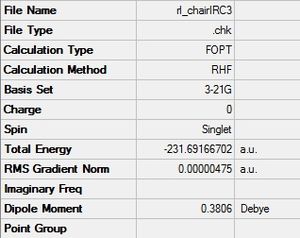 .log file .log file
|
Optimizing the boat transition structure
The QST2 method was used in order to optimize the boat structure. The first step was to number the molecules of the reactant and products in order to ensure the correct [3,3] reaction. Two of the Ci optimized molecule were copied into a new file in order to see the reactant and product side by side. The numbers were changed accordingly.
The job type was selected as Opt+Freq, with TS (QST2) selected. The HF method and 3-21G basis set was used again.
The job fails however, and results in a chair-like transition state that is more dissociated. What the calculation did was that it only translated the allyl fragment without considering rotation around the central bonds.
Thus the structures were then modified to have the C-C-C-C dihedral angle at 0°, and the C-C-C inside angles at 100°. This was done for both structures.
| Before | After |
|---|---|
 |

|
The job was set up again with the same options, and this time the calculation converged.
| Structure | Summary & .log file | Imaginary vibration animation |
|---|---|---|
 |
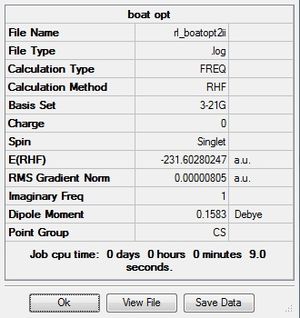 .log file .log file |
Link to animation |
The imaginary frequency is -840 cm-1.
This shows that sometimes the guessed structure needs to be close to the desired minimum. It can be seen here that changing the dihedral angles and the inner c-c-c angles has allowed gaussian to correctly give the boat, rather than the chair, TS. The final energy here is -231.60280247 a.u., whereas for the chair transition state the final energy is -231.61932246 a.u.. This shows that the chair transition state is slightly more stable than the boat TS. The C-C bond length for the boat TS is 2.14Å, which is longer than that for the chair (2.02Å). This also supports the fact that the chair TS is more stable, as a shorter bond is stronger and thus more stable. The CH2 groups causes more destabilization in the boat TS as they are closer together and in the same plane.
The imaginary frequency obtained in the chair TS was 818 cm-1, and for the boat it is slightly higher at 840 cm-1. Both the animations show one end bond breaking and the other end of the molecule bond making.
Since the same method and basis set was used to obtain the chair and boat TS, the two different methods can be compared. Both of the TS (Berny) and TS (QST2) methods show to be quite accurate in optimizing the TS. However, the latter method is a lot more tedious as the atoms need to be re-numbered. Thus if the reactants and products are quite large, this will prove to be too time consuming. Thus the TS (Berny) method should be sufficient enough for these types of calculations.
Activation energies
This is the same as for the earlier optimizations:
Sum of electronic and zero-point Energies= -231.466698 Sum of electronic and thermal Energies= -231.461339 Sum of electronic and thermal Enthalpies= -231.460394 Sum of electronic and thermal Free Energies= -231.495204
The data above gives energy information taken at 298.15 K.
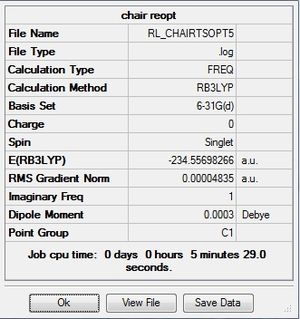
Chair optimization comparison
As described before, the DFT B3LYP/6-31G(d) method and basis set are more accurate than the HF/3-21G method and basis set. The latter was used to initially optimize the chair TS, then the former was used to re-optimize it.
| Parameter | HF/3-21G | DFT B3LYP/6-31G(d) |
|---|---|---|
| Structure |  |
|
| Inter-fragment distance (Å) | 2.02 | 1.97 |
| C-C bond length (Å) | 1.39 | 1.41 |
| C-C-C bond angle (°) | 120.5 | 120.0 |
| Dihedral angle (°) | 68.4 | 65.2 |
| Imaginary vibration (cm-1) | -818 | -566 |
| Final Energy (a.u.) | -231.61932239 | -234.55698266 |
| Summary & .log file |  .log file .log file |
 .log file .log file
|
As stated before, optimizations with different methods and basis sets cannot be directly compared, but here instead it is used as a way to confirm that the DFT method is more accurate in its calculation. The final energy shows that the DFT method is more accurate as the difference in energy shows a more stable minimum found. The inter-fragment distance is also shorter for the DFT method, showing a stronger bond. There is also a very large difference in imaginary vibration wavenumber. The HF method has one that is a lot higher than that of the DFT method. A larger wavenumber means a less stable energy, thus the DFT method has a lower wavenumber in comparison to the HF method.
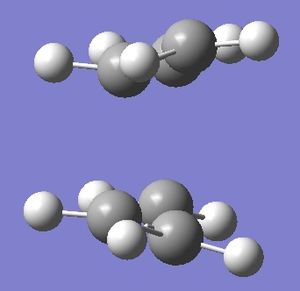
Boat optimization comparison
The same thing was carried out for the boat TS.
| Parameter | HF/3-21G | DFT B3LYP/6-31G(d) |
|---|---|---|
| Structure |  |
|
| Inter-fragment distance (Å) | 2.14 | 2.21 |
| C-C bond length (Å) | 1.38 | 1.39 |
| C-C-C bond angle (°) | 121.7 | 122.3 |
| Dihedral angle (°) | 64.8 | 64.1 |
| Imaginary vibration (cm-1) | -840 | -531 |
| Final Energy (a.u.) | -231.60280247 | -234.54309271 |
| Summary & .log file |  .log file .log file |
 .log file .log file
|
Again there is a different method used so a direct comparison is difficult, however it can be seen again that the boat TS is more accurately optimized with the DFT method. Again there is a huge difference in the imaginary vibration, as with the chair TS, however unlike the chair TS the inter-fragment distance increased with the DFT method. Thus the initial rationalization may be incorrect.
Calculating the activation energies
Sum of electronic and zero-point Energies= -234.414931 Sum of electronic and thermal Energies= -234.409011 Sum of electronic and thermal Enthalpies= -234.408067 Sum of electronic and thermal Free Energies= -234.443815
The table above corresponds to the energies of the chair TS with the DFT B3LYP/6-31G(d) method and basis set.
Sum of electronic and zero-point Energies= -234.402335 Sum of electronic and thermal Energies= -234.396001 Sum of electronic and thermal Enthalpies= -234.395057 Sum of electronic and thermal Free Energies= -234.431745
The table above corresponds to the energies of the boat TS with the DFT B3LYP/6-31G(d) method and basis set.
The values are all very similar, with the ones for the boat lower, showing that the chair TS is more stable than the boat TS.
Diels-Alder Cycloaddation Reactions
Cis-butadiene and ethylene
The diene in this reaction is cis-butadiene, which is a conjugated 4π e- system. The dienophile is ethylene, which is a 2π e- system. Thus this reaction is a [4+2] cycloaddition reaction, also known as a diels-alder reaction.
Optimization and HOMO-LUMO analysis
Both the diene and dienophile were optimized initially using the HF method with the 3-21G basis set. Both were then further optimized using the DFT method with B3LYP 6-31G(d) basis set.
These optimizations gave the following .log files: HF/3-21G butadiene optimization, DFT/B3LYP butadiene optimization; HF/3-21G ethylene optimization, DFT/B3LYP ethylene optimization.
The final structure of the diene gave a C2v point group, a final energy of -155.98594960 a.u., a dipole moment of 0.09 Debye, and a RMS gradient norm less than 0.001, which shows the optimization worked. The final structure of the dienophile gave a D2h point group, a final energy of -78.58745827 a.u., a dipole moment of 0.00 Debye, showing it is highly symmetrical, and a RMS gradient norm less than 0.001. These results are shown in the following table:
| 1,3-butadiene | ethylene |
|---|---|
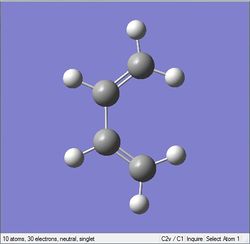 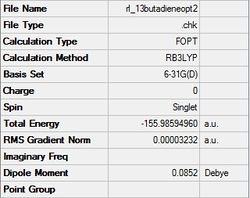 |
 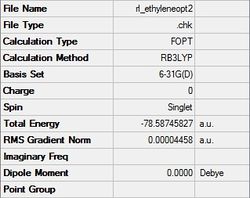
|
Next, a frequency calculation was run using the DFT optimized files of each molecule. This will give the ability to visualize the HOMO-LUMO molecular orbitals (MOs). The Semi-Empirical method was used with the AM1 basis set.
This gave the following .log files: MO analysis of butadiene; MO analysis of ethylene.
The .chk files were used in order to visualize the HOMO and LUMO orbitals of each molecule. The visualization of these MOs will help understand the reaction by looking at the symmetry of the orbitals with respect with the σv plane:
| 1,3-butadiene | |||
|---|---|---|---|
| HOMO | LUMO | Summary | |
| MO | 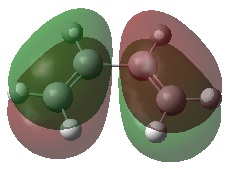 |
 |
|
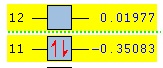
| Energy (a.u.) | -0.35083 | 0.01977 | |
| Symmetry | Antisymmetric | Symmetric | |
| ethylene | |||
|---|---|---|---|
| HOMO | LUMO | Summary | |
| MO | 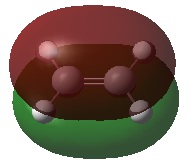 |
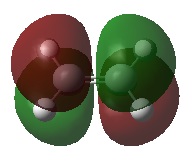 |
|
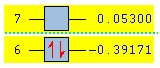
| Energy (a.u.) | -0.39171 | 0.05300 | |
| Symmetry | Symmetric | Antisymmetric | |
By looking at these MOs, it can be seen that the HOMO of 1,3-butadiene and the LUMO of ethylene are both antisymmetric, showing that they will have favorable overlap. Thus it can be expected that these two MOs will interact. The HOMO-LUMO gap here is 0.40383 a.u.. Similarly, the HOMO of ethylene and the LUMO of 1,3-butadiene are both symmetric, showing favorable overlap. Thus it can be expected that these two MOs will interact. The HOMO-LUMO gap here is 0.41248 a.u..
The smaller HOMO-LUMO gap will be favored as this means the overlap will be better and thus the interaction will be stronger. This means that the splitting and the stabilization of the resultant molecule will be greater.
This type of reaction is a 2N+2 reaction, with n=2. Thus since this is a thermodynamically occuring reaction it is a suprafacial one. The two fragments form the cyclic compound. Since the orbitals have similar symmetry and the energy gap isn't too great, then the orbitals will be able to interact quite well.
The HOMO=LUMO gap with the HOMO as butadiene and LUMO of ethylene is smaller, and thus this is the more favored combination of MOs. Thus this makes sense with the definition of the butadiene as the diene and the ethylene as the dienophile in this type of reaction.
Transition state analysis
For this analysis, the simplest method was used as it proved accurate enough and less tedious.
The initial guess of the structure was the ethylene a bit above the butadiene. First, the job was set to Opt+Freq, with method HF and basis set 3-21G. The force constants were calculated once and the keyword Opt=NoEigen was used as well to ensure the calculation doesn't crash. The second time the reaction was run the same options were used except with DFT method and B3LYP/6-31G(d) basis set. This gave the following results:
| Parameter | HF/3-21G | DFT B3LYP/6-31G(d) |
|---|---|---|
| Structure | 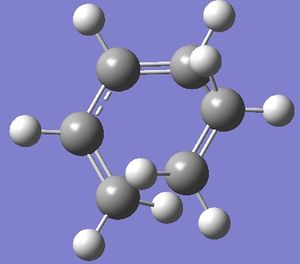 |

|
| Imaginary frequency (cm-1) | -820 | -524 |
| Final energy (a.u.) | -231.60320850 | -234.544 |
| Summary & .log file | 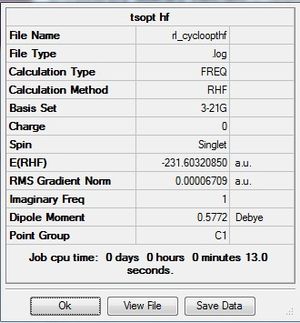 .log file .log file |
 .log file .log file
|
These results are similar to those of the butadiene and ethylene, as the imaginary frequency values and energies confrim the DFT method is a better method.
MO analysis of the HOMO & LUMO of the TS
For this the DFT B3LYP/6-31G(d) method was used.
| Parameter | HOMO | LUMO |
|---|---|---|
| MO structure |  |

|
| MO energy (a.u.) | -0.2170 | -0.00166 |
| Symmetry | Asymmetric | Symmetric |
| Summary & .log file | 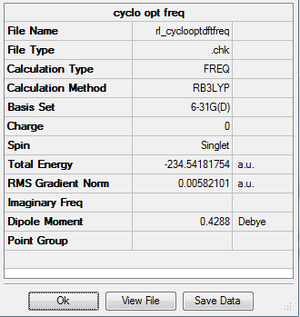 .log file .log file |
|
These can be compared like those of butadiene and ethylene. The symmetry shows that the two reactants form the product via a concerted cycloaddition, with an electron rich 1,3-butadiene HOMO and an empty π* orbital of ethylene LUMO.