Rep:Mod:ray2310
The molecule of BH3
Optimisation using Method B3LYP and Basis Set of 3-21G
Calculation method:B3LYP/3-21G
The optimised B-H bond length is 1.19 Angstrom.
The optimised H-B-H bond angle is 120.0 degrees.
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000350 0.001800 YES RMS Displacement 0.000229 0.001200 YES Predicted change in Energy=-4.546985D-08 Optimization completed. -- Stationary point found.
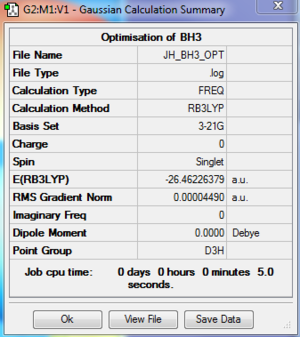
Optimisation file: File:JH BH3 321G file.LOG
Optimisation using Method B3LYP and Basis Set of 6-31G (d,p)
Calculation method:B3LYP/6-31G(d,p)
The optimised B-H bond length is 1.19 Angstrom.
The optimised H-B-H bond angle is 120.0 degrees.
Optimisation file: File:JH BH3 OPT 631G.LOG
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000049 0.001800 YES RMS Displacement 0.000025 0.001200 YES Predicted change in Energy=-9.283977D-10 Optimization completed. -- Stationary point found.
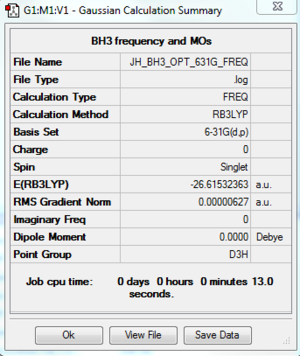
E(BH3)= -26.61532 a.u.
Low frequencies --- -6.8246 -1.4177 -0.0056 0.7248 7.6960 7.8255 Low frequencies --- 1162.9713 1213.1658 1213.1685
BH3 |
Frequency file: File:JH BH3 OPT 631G FREQ.LOG
Vibrational spectrum of BH3
wavenumber (cm-1) Intensity (arbitrary units) symmetry IR active? type 1163 93 A1 yes out-of-plane bend 1213 14 E very slight bend 1213 14 E very slight bend 2582 0 A1 no symmetric stretch 2716 126 E yes asymmetric stretch 2716 126 E yes asymmetric stretch

There are less than six peaks in the spectrum because there are only five IR active vibrational modes. Furthermore, the existence of degenerate modes leads to fewer peaks in the spectrum. There are two degenerate bending modes at 1213 cm-1 and two degenerate asymmetric stretching modes at 2716 cm-1. Hence, there are only 3 peaks in the IR spectrum.
Smf115 (talk) 19:15, 23 May 2018 (BST)Correct assigment of the vibrational modes and explaination of the 3 peaks visualised. However, the symmetries of the vibrations are incorrect suggesting that the molecule has the wrong point group.
Molecular Orbitals of BH3
The MO energy levels from 1 to 8 are explored and illustrated as shown below. The first four MOs are occupied and the LUMO is the fifth MO.
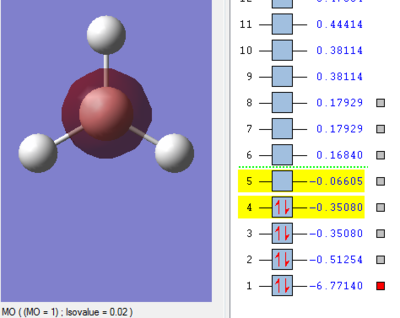
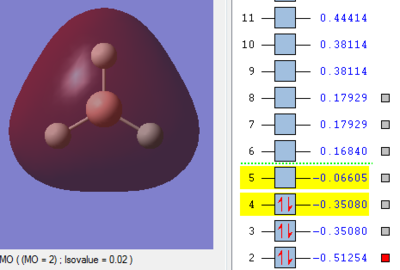
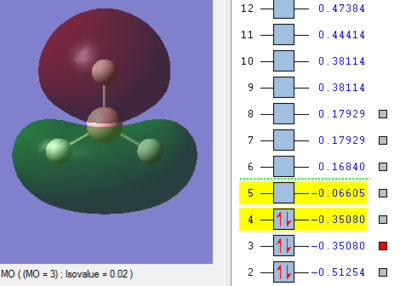

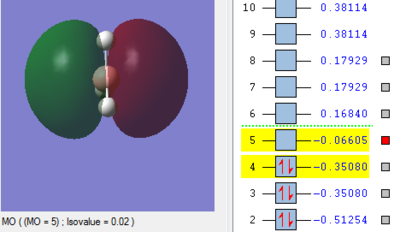
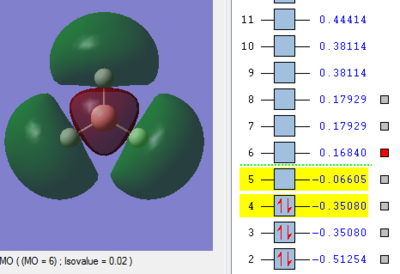
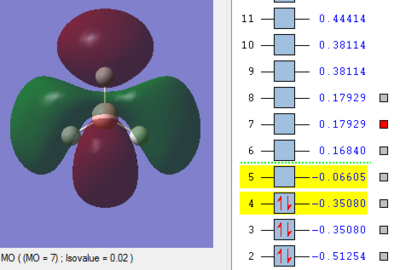

Smf115 (talk) 19:15, 23 May 2018 (BST)Good and clear visualisation of the MOs required.
Comparison of real MOs to "LCAO" MOs
The real MOs are compared to the "LCAO" MOs, which are illustrated in the diagram shown below. [1]

Through the comparison, it is observed that the computed MOs have slightly different shapes of surfaces from those in the LCAO MOs diagram. However, there are 3 occupied molecular orbitals filled by 6 electrons in both "LCAO" and computed MOs diagrams. The computed MOs diagram also shows the 1s orbital of boron. It also shows that the LUMO, MO 5, is non-bonding as predicted in the LCAO diagram. Since the LUMO is low in energy and non-bonding, the filling of electrons into it will not affect the B-H bonds. Furthermore, both MOs diagrams indicate that the molecule is a Lewis Acid due to the existence of non-bonding LUMO to accept electrons.
The comparison suggests that the LCAO (linear combination of atomic orbitals) provides an approximation for the molecular orbitals of a molecule. It does not have a high degree of accuracy but it manages to reflects the real situation to some extent. It is useful to predict the shapes of molecules and the bond strengths efficiently using a few basic rules.
Overall, the computed MOs diagram conforms to the predicted diagram.
Calculation of Association Energy
Optimisation of NH3
Calculation method: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000039 0.001800 YES RMS Displacement 0.000013 0.001200 YES Predicted change in Energy=-3.862150D-10 Optimization completed. -- Stationary point found.

E(NH3)= -56.55777 a.u.
Low frequencies --- -8.5646 -8.5588 -0.0047 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
NH3 |
Frequencies file: File:JH NH3 631G FREQ.LOG
Optimisation of NH3BH3
Calculation method: B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000113 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000701 0.001800 YES RMS Displacement 0.000347 0.001200 YES Predicted change in Energy=-1.717355D-07 Optimization completed. -- Stationary point found.

E(NH3BH3)= -83.22469 a.u.
Low frequencies --- -12.2585 -0.0008 -0.0004 -0.0003 19.3973 43.3115 Low frequencies --- 266.3451 632.1223 638.3345
NH3BH3 |
Frequencies file: File:JH NH3BH3 631G FREQ.LOG
Calculation of Association Energy of NH3BH3
E(BH3)= -26.61532 a.u.
E(NH3)= -56.55777 a.u.
E(NH3BH3)= -83.22469 a.u.
△E=E(NH3BH3)-[E(BH3)+E(NH3)]
△E=-0.05160 a.u.
△E=-135 kJ/mol
The calculated association energy reflects the energy released by forming the B-N dative bond. The B-N dative bond is a weak bond in comparison to other bond enthalpies. [2]
Smf115 (talk) 19:13, 23 May 2018 (BST)Correct calculation and consideration given to the accuracy of the final result. Good reference used but it would be good to quote a specific bond dissociation energy as comparison.
Optimisation of BBr3 using a mixture of basis-sets and pseudo-potentials
Calculation method:B3LYP/6-31G(d,p)LANL2DZ
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000018 0.001200 YES Predicted change in Energy=-4.106155D-10 Optimization completed. -- Stationary point found.

E(BBr3) = -64.43645 a.u.
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
BBr3 |
Frequency file:File:JH BBr3 freq.log
Aromaticity
There are four conditions that determine the aromaticity of a molecule. If any of these conditions is violated, then the molecule is not considered to be aromatic.
- An aromatic molecule must be cyclic. - An aromatic molecule must be planar. - An aromatic molecule must have a conjugated system. - An aromatic molecule must have [4n+2] pi electrons. (Hückel's rule)
There must be a continuous ring of p-orbitals so that every atom around the ring is capable of conjugation with each other. This also allows for the pi electrons to be delocalised around the ring, which increase the stability. Hence, the molecule cannot be represented by one structure but rather a resonance hybrid.
Benzene
Calculation method:B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000087 0.000300 YES Maximum Displacement 0.000757 0.001800 YES RMS Displacement 0.000321 0.001200 YES Predicted change in Energy=-3.962814D-07 Optimization completed. -- Stationary point found.

E(benzene)=-232.25821 a.u.
Low frequencies --- -2.1456 -2.1456 -0.0089 -0.0043 -0.0043 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
Benzene |
Frequency file: File:JH BENZENE FREQ.LOG
Borazine
Calculation method:B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000207 0.000450 YES RMS Force 0.000066 0.000300 YES Maximum Displacement 0.000318 0.001800 YES RMS Displacement 0.000101 0.001200 YES Predicted change in Energy=-1.131367D-07 Optimization completed. -- Stationary point found.

E(borazine)= -242.68458 a.u.
Low frequencies --- -12.8733 -12.5498 -8.3846 -0.0110 0.0434 0.0625 Low frequencies --- 289.0631 289.0745 403.8252
Borazine |
Frequency file:File:JH BORAZINE FREQ.LOG
Comparison of Charge Distribution between Benzene and Borazine


Benzene Borazine Charge on C -0.239 N/A Charge on H 0.239 0.432 (attached to N) and -0.077 (attached to B) Charge on B N/A 0.747 Charge on N N/A -1.102
In the molecule of benzene, carbon (2.55 Pauling units) is slightly more electronegative than hydrogen (2.20 Pauling units). Hence, the carbon atom bears a negative charge indicating that it draws electron density towards itself. In the molecule of borazine, nitrogen (3.04 Pauling units) is more electronegative than boron and hydrogen. Thus, it bears a negative charge and the hydrogen attached to it has a positive charge. Since boron (2.04 Pauling units) is slightly more electropositive than hydrogen (2.20 Pauling units), it bears a positive charge while the hydrogen attached to boron has a negative charge.
Smf115 (talk) 18:53, 23 May 2018 (BST)Nice explaination of the charges due to the electronegativities of the atoms. However, the answer needed to be developed a bit further, explaining the difference between the polarisation of the N-H and B-H bonds more clearly, for example. Additionally, the charge distribution of the molecules should be highlighted by the same colour range to allow for clear comparison.
Comparison of Comparative MOs between Benzene and Borazine


MO 7 is the valence orbital at the lowest energy level. This σ orbital is symmetric and in-phase bonding in both benzene and borazine. The benzene MO is more symmetrical than that of borazine. The borazine MO does not cover all the H atoms, which means that it lacks the contribution from some H atoms. It is clearly illustrated that the H atoms attached to the boron atoms do not contribute to the σ1 orbital. It is because the nitrogen is more electronegative and has a higher electron density. Thus, the MO is not evenly distributed around the ring due to the polarity of the pi-system. The shape of the MO corresponds to the fact that both molecules have a planar and conjugated structure.


MO 14 of benzene and MO 15 of borazine are the σ2 orbitals. The σ orbital is also highly symmetric and out-of-phase bonding in both molecules. The planar MO reflects the fact that both molecules have a planar structure.


MO 21 is the valence orbital at the highest energy level. This pi orbital is out-of-phase bonding in both molecules but the benzene MO is more symmetrical than that of borazine. The borazine MO does not cover all the H atoms, which indicates that not all H atoms contribute to the MO evenly. This is another example of the MO being affected by the polarity of the pi-system. The more electronegative H atoms, which are attached to the electropositive boron atoms, do not contribute to the MO as much as those attached to the electronegative nitrogen atoms. Thus, the concept of overlapping pz AOs is not sufficient enough to support all the aromatic molecules.
Traditionally, the origin of aromaticity is associated with the planar structure. However, it is presently well known that aromaticity does not necessarily have to be planar and planarity of aromatic molecules can be destroyed easily. For example, benzene in the crystalline state at 20 K is not planar but has a chair conformation due to the the strong intermolecular forces in the crystal lattice. However, this does not violate the fact that benzene is an aromatic molecule. Furthermore, pseudoaromaticity can arise from the aromaticity of non-alternant pi-electron system. [3] Overall, the concept of overlapping pz AOs forming a planar pi system is not sufficient to describe the aromaticity. Furthermore, the criteria for defining the aromaticity of a cyclic delocalised pi-electron system has been updated as shown below.
- It is more stable than its olefinic analogues by an energy called “resonance energy”, RE (nowadays oftennamed aromatic stabilization energy, ASE); - It has bond lengths intermediate between those oftypical single and double bonds; - When it is put in an external magnetic field a p-elec-tron ring current is induced, leading to an increased dia-magnetic susceptibility and typical diatropic chemicalshifts of exocyclic protons in 1H NMR spectra; - In addition, aromatic compounds generally undergo reac-tions in which the p-electron structure is conserved (theso-called aromatic substitution). [3]
Smf115 (talk) 19:12, 23 May 2018 (BST)Good identification of the MOs as pi- or sigma- and as bonding or antibonding. However, the comparison could have been a bit more detailed, considering the actual symmetry of the orbitals or the contributing AOs for example. The lay out of the updated criteria for aromaticity is good and the concept of requiring a planar structure is discussed well. To improve the key concepts inclusing Huckel's rule could have been discussed further and other aspects of aromaticity. How MO 21 illustrates how overlapping pz AOs is a bad description of aromaticity is a good idea that isn't explained clearly enough to show how the conclusion is reached. The attempt to use the MOs visualised to explain this is good though.
Smf115 (talk) 19:12, 23 May 2018 (BST)Overall a good first section with more relevant discussion required in places for the project section.
References
- ↑ Hunt. P., 'Lecture 4 Tutorial Problem Model Answers', lecutre notes, Molecular Orbitals in Inorganic Chemistry CHEM50001, Imperial College London.
- ↑ W., P., 2010. Shriver & Atkins' Inorganic Chemistry. Oxford University Press.
- ↑ 3.0 3.1 Palusiak, M. and Krygowski, T. (2007). Application of AIM Parameters at Ring Critical Points for Estimation of π-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings. Chemistry - A European Journal, 13(28), pp.7996-8006.
Cite error: <ref> tag with name "enthalpies" defined in <references> group "" has no content.
Cite error: <ref> tag with name "aromatic" defined in <references> group "" has no content.
