Rep:Mod:qwt11 inorg ionicliquids
Mini Project - Ionic Liquids: Designer Solvents
Qian Wen Tan
CID: 00700342
Introduction
Ionic liquids are ionic salts in the liquid state due to their low melting points. This is an anomaly from the usual ionic salts which have high melting points due to the high lattice energies caused by the strength of the ionic bonds. Hence, ionic liquids have their own special properties that can be engineered accordingly, leading to them being known as designer solvents. In this computational project, the properties of 3 'onium' ions and the influence of functional groups are explored.
Comparison of selected 'onium' cations
The selected 'onium' cations are [N(CH3)4]+, [P(CH3)4]+ and [S(CH3)3]+.
[N(CH3)4]+
Data
DOIs
Optimisation: DOI:10042/26160
Frequency Analysis:DOI:10042/26161
Population Analysis:DOI:10042/26162
Summary of results
| Calculation | Optimisation using 6-31G(d,p) | Frequency Analysis | Population Analysis |
|---|---|---|---|
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FREQ | SP |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 | 1 |
| Spin | Singlet | Singlet | Singlet |
| E(RB3LYP) | -214.18126735 a.u. | -214.18126735 a.u. | -214.18126735 a.u. |
| RMS Gradient Norm | 0.00003015 a.u. | 0.00002996 a.u | - |
| Dipole Moment | 0.0002 Debye | 0.0001 Debye | 0.0002 Debye |
| Point Group | C1 | C1 | C1 |
| Job cpu time | 0 days 0 hours 9 minutes 24.3 seconds | 0 days 0 hours 9 minutes 6.3 seconds | 0 days 0 hours 1 minutes 12.7 seconds |
Final sets of forces and displacements for optimisation using 6-31G(d,p)
Item Value Threshold Converged?
Maximum Force 0.000081 0.000450 YES
RMS Force 0.000020 0.000300 YES
Maximum Displacement 0.000667 0.001800 YES
RMS Displacement 0.000189 0.001200 YES
Predicted change in Energy=-6.645118D-08
Optimization completed.
-- Stationary point found.
Final sets of forces and displacements for frequency analysis
Item Value Threshold Converged?
Maximum Force 0.000071 0.000450 YES
RMS Force 0.000030 0.000300 YES
Maximum Displacement 0.001133 0.001800 YES
RMS Displacement 0.000312 0.001200 YES
Predicted change in Energy=-1.258655D-07
Optimization completed.
-- Stationary point found.
Low frequencies
Low frequencies --- -19.4468 -12.6357 -0.0006 -0.0004 0.0009 5.1478 Low frequencies --- 178.8418 282.0168 285.4548
Optimisation was performed using the basis set 6-31G(d,p). The RMS gradient norm is <0.001 and close to 0 for all calculations. In addition, all calculations also converged. The energy is calculated to be -214.18126735 a.u. for all. The 6 low frequencies (first line) are also within the required range of +/-30cm-1. In addition, the second set of frequencies have positive values, indicating minimum energies. All 3 calculations have similar dipole moments.
Selected Molecular Orbitals (MOs)
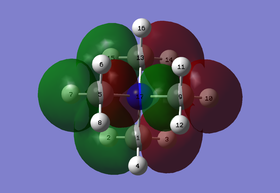
MO analysis were performed on 5 selected MOs of [N(CH3)4]+. These are MO #6, #10, #15, #17 and #21.
(I) MO 6: highly bonding
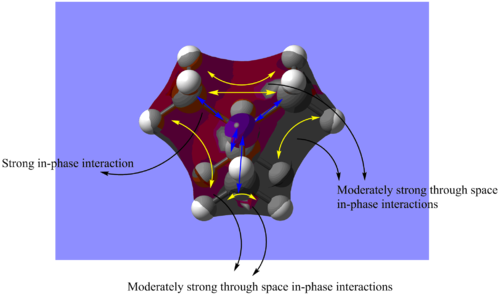
Figure 1.1: Molecular Orbital 6 - highly bonding
Referring to Figure 1.1, MO 6 is a highly bonding MO where there are strong in-plane interactions between the s atomic orbitals of N and the C atoms (blue arrows), while the H atoms are not involved. In addition, there are also multiple moderately strong through space interactions between the orbitals(yellow arrows). There is no presence of any nodes as all the orbitals are in phase. Overall, this leads to a highly bonding MO. The MO is also highly delocalised with the orbitals overlapping such that the overall orbital covers nearly the whole molecule. The calculated energy is -1.19646a.u..
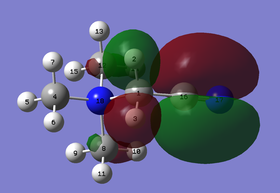
(I) MO 10: bonding
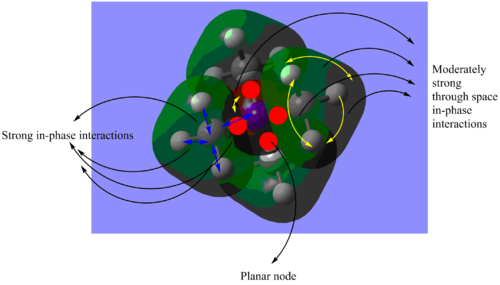
Figure 1.2: Molecular Orbital 10 - bonding
Referring to Figure 1.2, MO 10 is a bonding orbital with 4 planar nodes (red circles). The nodes are the nodes in each p orbital of the C atoms. At each methyl group, the p orbital of C atom overlaps with the s orbital of the H atoms (nlue arrows). The orbitals formed have moderately strong through space in-phase interactions (yellow arrows). However, the through space in-phase interactions between methyl groups are weak. As a result the orbitals are localised at each methyl group. The opposite phase of the p orbitals of the C atoms also overlap with the s orbital of the N atom. As a result, there is strong out-of-phase interactions between the opposite phases. The central orbital is also quite localised on N. Overall the MO has more bonding interactions than anti-bonding interactions. The calculated energy is -0.80745 a.u..
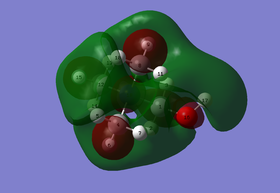
(I) MO 15: non-bonding
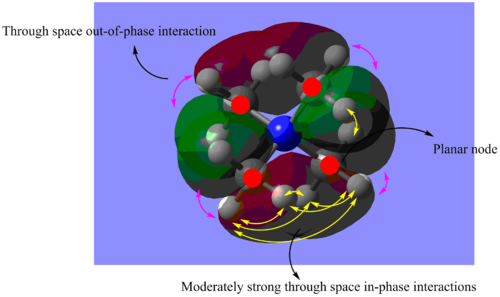
Figure 1.3: Molecular Orbital 15 - non-bonding
Referring to Figure 1.3, there are 4 planar nodes present at each C atom in MO 15. As a result, s orbitals of 2 H atoms of one methyl group will overlap with the p orbital of the C atom with in-phase interactions. This orbital will then form through space in-phase interactions with another similarly formed orbital at the methyl group beside it(yellow arrows). The remaining H atom will then form strong through space in-phase interaction with another H atom from another methyl group (yellow arrow), in addition to forming orbital overlap with the other phase of the p orbital of C atom. This pattern is consistent for all methyl groups present. Due to the presence of nodes, there is change of phase in the orbitals. Hence, strong through space out-of-phase interactions can be observed between H atoms in a single methyl group (pink arrows) and between orbitals with different phases in general. The N atom does not participate in this MO. The overall MO is non-bonding as the interactions are cancelled out by the anti-bonding interactions. The Mo is also delocalised as orbitals are formed from through space overlaps. The calculated energy is -0.62246a.u..
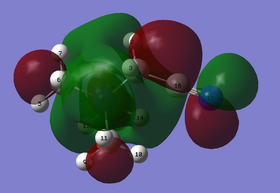
(I) MO 17: anti-bonding

Figure 1.4: Molecular Orbital 17 - anti-bonding
Referring to Figure 1.4, MO 17 consists of 4 planar nodes at each C atom. 2 of the H atoms are not involved. Strong in-phase interaction can be seen between 2 H atoms in 2 of the methyl groups (yellow arrows), which also overlaps with p orbital of the C atom that has the same phase. The s orbital remaining H atom in the methyl group then overlaps in-phase with the other phase of the p orbital of the C atom. This occurs for all the methyl groups. The N atom is not involved in this MO. As the orbitals are of alternating phases, weak through space out-of-phase interactions (blue arrows) and strong out-of-phase interactions (pink arrows) can be observed, with the strength dependent on the distance between the orbitals. The change of phases are due to the presence of the planar nodes. In addition, there is also weak through space in-phase interactions between orbitals of the same phase (purple arrow). Overall, the MO is considered to be anti-bonding as there are many out-of-phase interactions. The MO is also largely delocalised due to the through space interactions. The calculated energy is -0.58034a.u..
(I) MO 21: highly anti-bonding

Figure 1.5: Molecular Orbital 21: highly anti-bonding
Referring to Figure 1.5, MO 21 consists of 5 planar nodes at all the C atoms and the N atom. There are presence of strong in-phase overlap of the s orbitals of 2 H atoms in methyl group with the p orbital of the C atom. This occurs for all the methyl groups but 2 of the methyl groups have the same phase while the other 2 are of different phase. The remaining H atom then overlaps with the p orbital of the N atom and the other s orbital of the H atom on another methyl group. This also happens for the last 2 H atoms but with an opposite phase. As a result, there are multiple strong out-of-phase interactions(pink arrows). Hence, the overall MO is highly anti-bonding and delocalised. The calculated energy is -0.57933a.u..
[P(CH3)4]+
Data
DOIs
Optimisation: DOI:10042/26163
Frequency Analysis:DOI:10042/26164
Population Analysis:DOI:10042/26165
Summary of results
| Calculation | Optimisation using 6-31G(d,p) | Frequency Analysis | Population Analysis |
|---|---|---|---|
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FREQ | SP |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 | 1 |
| Spin | Singlet | Singlet | Singlet |
| E(RB3LYP) | -500.82701295 a.u. | -500.82701307 a.u. | -500.82699130 a.u. |
| RMS Gradient Norm | 0.00000467 a.u. | 0.00000445 a.u. | - |
| Dipole Moment | 0.0001 Debye | 0.0001 Debye | 0.0002 Debye |
| Point Group | C1 | C1 | C1 |
| Job cpu time | 0 days 0 hours 22 minutes 5.2 seconds | 0 days 0 hours 20 minutes 25.0 seconds | 0 days 0 hours 1 minutes 53.5 seconds |
Final sets of forces and displacements for optimisation using 6-31G(d,p)
Item Value Threshold Converged?
Maximum Force 0.000011 0.000015 YES
RMS Force 0.000003 0.000010 YES
Maximum Displacement 0.000051 0.000060 YES
RMS Displacement 0.000017 0.000040 YES
Predicted change in Energy=-1.415870D-09
Optimization completed.
-- Stationary point found.
Final sets of forces and displacements for frequency analysis
Item Value Threshold Converged?
Maximum Force 0.000021 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000476 0.001800 YES
RMS Displacement 0.000173 0.001200 YES
Predicted change in Energy=-4.142589D-09
Optimization completed.
-- Stationary point found.
Low frequencies
Low frequencies --- -8.3301 -0.0012 0.0026 0.0032 2.1241 15.6018 Low frequencies --- 156.3266 191.6596 192.4282
Optimisation was performed using the basis set 6-31G(d,p). The RMS gradient norm is <0.001 and close to 0 for both. In addition, all calculations also converged. The 6 low frequencies (first line) are also within the required range of +/-30cm-1 as tight convergence criteria was chosen and the keyword 'int=ultrafine scf(conver=9)' was used to ensure that. In addition, the second set of frequencies have positive values, indicating minimum energies. However, upon close inspection of the energy levels, all of them are different for all 3 calculations although frequency analysis and population analysis were done using the optimised molecule from the optimisation using 6-31G(d,p). This occurred despite repeating the calculations. Having consulted the demonstrator, I was advised to leave the calculations as they are since the same file was used for further calculations. All 3 calculations have similar dipole moments.
[S(CH3)3]+
Data
DOIs
Optimisation: DOI:10042/26188
Frequency Analysis:DOI:10042/26189
Population Analysis:DOI:10042/26195
Summary of results
| Calculation | Optimisation using 6-31G(d,p) | Frequency Analysis | Population Analysis |
|---|---|---|---|
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FREQ | SP |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 | 1 |
| Spin | Singlet | Singlet | Singlet |
| E(RB3LYP) | -517.68327532 a.u. | -517.68327532 a.u. | -517.68326973 a.u. |
| RMS Gradient Norm | 0.00000328 a.u. | 0.00000326 a.u. | - |
| Dipole Moment | 0.9651 Debye | 0.9651 Debye | 0.9651 Debye |
| Point Group | C1 | C1 | C1 |
| Job cpu time | 0 days 0 hours 23 minutes 16.3 seconds | 0 days 0 hours 8 minutes 58.5 seconds | 0 days 0 hours 0 minutes 36.3 seconds. |
Final sets of forces and displacements for optimisation using 6-31G(d,p)
Item Value Threshold Converged?
Maximum Force 0.000097 0.000450 YES
RMS Force 0.000041 0.000300 YES
Maximum Displacement 0.001015 0.001800 YES
RMS Displacement 0.000312 0.001200 YES
Predicted change in Energy=-1.682889D-07
Optimization completed.
-- Stationary point found.
Final sets of forces and displacements for frequency analysis
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.001786 0.001800 YES
RMS Displacement 0.000618 0.001200 YES
Predicted change in Energy=-1.159186D-08
Optimization completed.
-- Stationary point found.
Low frequencies
Low frequencies --- -4.3477 -0.0008 -0.0008 0.0036 6.9781 9.4617 Low frequencies --- 161.8789 199.6201 200.6687
Optimisation was performed using the basis set 6-31G(d,p). The RMS gradient norm is <0.001 and close to 0 for both. In addition, all calculations also converged. The 6 low frequencies (first line) are also within the required range of +/-30cm-1. In addition, the second set of frequencies have positive values, indicating minimum energies. Tight convergence criteria was chosen and the keyword 'int=ultrafine scf(conver=9)' was used to ensure that the frequency analysis calculation converged. Once again, the problem of having different energies occurred despite repeating the calculations. As a result, the calculations were left as such as the optimised molecule was used for frequency analysis and population analysis. All 3 calculations have the same dipole moment of 0.9651D.
Comparisons between [N(CH3)4]+, [P(CH3)4]+ and [S(CH3)3]+
Comparison of geometries
In the following table, X is given to be the heteroatom, which can either be N, P or S.
| Molecules | [N(CH3)4]+ | [P(CH3)4]+ | [S(CH3)3]+ |
|---|---|---|---|
| X-C bond length/Å | 1.51 | 1.82 | 1.82 |
| C-H bond length/Å | 1.09 | 1.09 | 1.09 |
| H-C-H angle/o | 110.0 | 109.0 | 109.4/111.1 |
| H-C-X angle/o | 108.9 | 109.9 | 107.3/110.6 |
| C-X-C angle/o | 109.5 | 109.5 | 102.3 |
Bond lengths
The calculated C-N bond length of 1.51Å is close to the reported value of 1.496(2)Å[1] in [N(CH3)4][BrO3F2]. The calculated C-P bond length of 1.82Å is also close to the reported value of 1.830(5)Å[2] in [Co(CCH){P(CH3)3}4]. Finally, the calculated C-S bond length of 1.82Å is also in good agreement with the reported value of 1.813Å[3] in (SCH3)2.
It can be observed that the C-N bond is significantly shorter than the C-P and the C-S bond. This is because N is in the second period of the Periodic Table of Elements, while P and S are in the third period, hence it is much less diffused with a larger effective nuclear charge. As a result, there is less electron-electron repulsion during bond formation. In addition, the orbital size is much similar to that of C, which is beside it in the Periodic Table of Elements, hence there will be better orbital overlap between N and C as compared to between P and C or S and C. Hence, a stronger bond will be formed, leading to a shorter C-X bond. The calculated P-C and S-C bond lengths are the same as P and S are just beside each other in the Periodic Table of Elements, hence they will have similar orbital overlap with C.
All the C-H bond lengths are identical, indicating that the heteroatom has no influence on them.
Bond angles
The angles about C-X-C for [N(CH3)4]+ and [P(CH3)4]+ are 109.5o, which ties in with the tetrahedral geometry. In the cations, N and P each loses 1 valence electron to be left with 4 valence electrons. All 4 electrons on N and P are used for bonding with the 4 methyl groups. Hence, the geometry about N and P is tetrahedral, which is clearly seen from the 109.5o. Sulfur belongs to group 16 on the Periodic Table of Elements. Hence, after removing 1 valence electron, there will be 5 valence electrons left. Out of the 5 valence electrons, only 3 are used for bonding with 3 methyl groups, leading to a lone pair found on S. As a result, [S(CH3)3]+ has a trigonal pyramidal structure with an angle of 102.3o. The angle is smaller than that of [N(CH3)4]+ and [P(CH3)4]+ as the lone pair - bond pair repulsion is much greater. Hence the calculations have confirmed the structures of the 'onium' ions.
[S(CH3)3]+ is found to have 2 values each for the H-C-H bond angles and the H-C-S bond angles. This is due to the presence of the lone pair on S, which results in greater repulsion to the H atoms that are close to it. As a result the angle is reduced for the H-C-H and H-C-X angles for those H atoms close to S.
NBO Charge Analysis
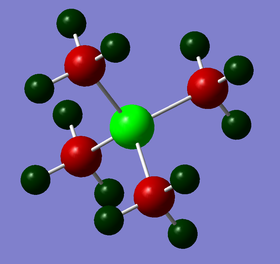
| Molecules | [N(CH3)4]+ | [P(CH3)4]+ | [S(CH3)3]+ |
|---|---|---|---|
| Charge by colour | 
|
|
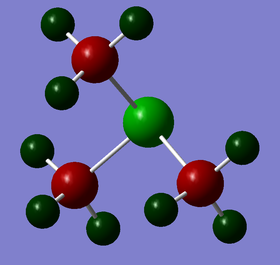
|
| Labelled charges | 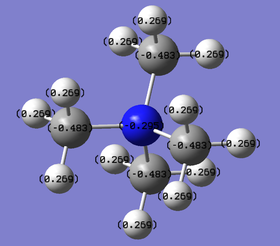
|

|
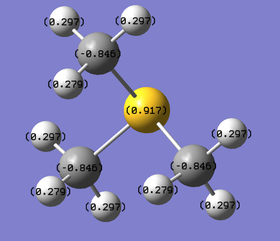
|
| Charge values | N: -0.295 C: -0.483 H: +0.269 |
P: +1.667 C: -1.060 H: +0.298 |
S: +0.917 C: -0.846 H: +0.297 |
The charge range is set to be -1.700 to +1.700 to allow proper comparison. Red indicates a negative charge and the lighter it is, the more negative the value. Similarly, green indicates positive charge, and the lighter it is, the more positive it is. Although all 3 cations are singly charged, they show different charge distribution as seen above.
The charges of the heteroatoms N, P and S tie in with their electronegativity where N > S> P. Hence, P is seen to have the highest positive charge of +1.667 while N is seen to be negatively charge with a value of -0.295. Comparing the charges on the C atoms in all 3 cations, it can be observed that they show great differences, with the C atom in [N(CH3)4]+ being the least negative (-0.483) while the C atom in [P(CH3)4]+ being the most negative (-1.060). This is in line with the previous argument; the C atom that is attached to the more negatively charge heteroatom will be relatively more positive. The H atoms for [P(CH3)4]+ and [S(CH3)3]+ have similar charge values. However, the H atoms in [N(CH3)4]+ are slightly less positive. This is due to the less negatively charged C atoms. Overall, all 3 cations have their charges summed up to 1, which is expected. However, although N is usually drawn to hold the formal +1 charge in the cation, it can be observed that it is still negatively charged due to its electronegativity.
NBO Population Analysis
| Molecules | Relative contributions/ % | Electronegativities[4] | Difference in electronegativities (X-C) |
|---|---|---|---|
| [N(CH3)4]+ | ( 33.65%) 0.5801* C 1 s( 20.78%)p 3.80( 79.06%)d 0.01( 0.16%) ( 66.35%) 0.8145* N 17 s( 25.00%)p 3.00( 74.96%)d 0.00( 0.03%) |
C: 2.55 N: 3.04 |
0.49 |
| [P(CH3)4]+ | ( 59.57%) 0.7718* C 1 s( 25.24%)p 2.96( 74.67%)d 0.00( 0.08%) ( 40.43%) 0.6358* P 17 s( 25.00%)p 2.97( 74.15%)d 0.03( 0.85%) |
C: 2.55 P: 2.19 |
0.36 |
| [S(CH3)3]+ | ( 48.67%) 0.6976* C 1 s( 19.71%)p 4.07( 80.16%)d 0.01( 0.14%) ( 51.33%) 0.7164* S 13 s( 16.95%)p 4.86( 82.42%)d 0.04( 0.63%) |
C: 2.55 S: 2.58 |
0.03 |
The NBO population analysis data above shows the % contribution of the C atom and the X atom (N/P/S) to the C-X bond. In general, the orbitals at C and X are all sp3 hybridised orbitals although the contribution from the s orbital and the p orbital slightly deviates for the C atoms in [N(CH3)4]+ and [S(CH3)3]+. It is also noted that the S atom has the largest deviation as it has more diffused orbitals so the hybridisation deviates from sp3. When looking at their relative contributions, the trend shows a decreasing contribution from the X atom where N >S > P. In particular, C contributes more to the C-X bond than P in [P(CH3)4]+.
This can be explained by looking at the respective electronegativities of the atoms and the difference in electronegativities between C and X. In general, all the C-X bonds are covalent with varying degree of ionic character according to the magnitude of the differences in electronegativities. The electronegativity difference in the C-X bond decreases from C-N > C-P > C-S. In a bond, the more electronegative atom is expected to have a larger relative contribution as it has a high tendency to draw the electron pair to itself. This is observed above, in each C-X bond, the more electronegative atom (N for [N(CH3)4]+, C for [P(CH3)4]+ and S for [S(CH3)3]+) shows a greater contribution. In addition, the relative contribution is related to the difference in electronegativity between C and X. For [N(CH3)4]+, the electronegativity difference (0.49) is the greatest, hence N contributes significantly more than C to the C-N bond. On the other hand, the electronegativity difference between C and S in [S(CH3)3]+ is very small, such that each of them contributes about the same % to the C-X bond, with S contributing slightly more as it is slightly more electronegative than C.
With such an observation, it will be expected that the electronegativity difference indicates that N should hold large negative charge while C should hold large positive charge in the C-N bond. Yet this is not observed in the charge distribution. In fact, the charge distribution shows a negative charge for N and an even more negative charge for C. This is because the N atom no longer has the usual 5 valence electrons, but instead, has only 4 valence electrons as a cation is formed. As a result, this will reduce the electronegativity of the N atom, hence decreasing its negative charge. In addition, the overall positive charge is delocalised throughout the cation and not localised on the N atom, hence the negative charge on N is maintained.
Further explanation is derived from the fact that C and N are beside each other in the Periodic Table of Elements. As a result, the orbital overlap in the formation of the C-N bond is large. This can lead to a contribution of the electronegativity on N to the C atom, which can then lead to a more negative charge than usual. More importantly, the C atoms are surrounded by electropositive H atoms. Given that the overall charge is +1, the overall charge distribution has to be distributed such that the sum of all the charges = 1 while at the same time, maintaining the negative charge on the electronegative N and the positive charge on the electropositive H atoms. As a result, this lead to negative charges on C atoms, despite them being more electropositive than N, which is unexpected. In this case, C-N bond has the highest ionic character out of all the C-X bonds due to the greatest electronegativity difference.
For the C-P bond, it can be seen that P is more electropositive than C. This also ties in with the charge distribution seen above, where P has a charge of +1.667 and C has a charge of -1.060. In this case, it is expected for C to have a negative charge as it is more electronegative relative to P. Furthermore, with the formation of a cation, the P atom has 1 less valence electron, leading to a greater positive charge. Since P is electropositive, the +1 charge will be localised on it. Furthermore, the C atoms are now surrounded by electropositive P atom and H atoms. Hence, they will be highly negatively charged. Overall, this corresponds to the % contribution where P contributes less as it is more electropositive. Once again, the C-P bond has ionic character as the electronegativity difference is 0.36.
For the C-S bond, there is very small electronegativity difference between C and S (0.03). Hence, the C-S bond can be considered non-polar and is highly covalent. This means that there is nearly equal % contribution from each atom to the C-S bond, which is observed. Although S is slightly more electronegative than C, it has a charge of +0.917 while C has a charge of -0.846. This contradictory data indicates that the overall +1 charge of the cation is localised on S.
Formal charge in [NR4]+
Traditionally, the 'formal' positive charge on N is shown to be localised on N in [N(CH3)4]+. This is because there is one valence electron removed from N to give only 4 valence electrons which will bond with the methyl groups. However, as seen previously, the N atom in [N(CH3)4]+ has a charge value of -0.295, implying that it is incorrect to draw the positive charge on N. Instead, this positive charge is delocalised to all the H atoms in [N(CH3)4]+ as they are the most electropositive atoms in the molecule.
Influence of functional groups
In order to observe the influence of functional groups on the ionic liquids, data were calculated for [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+.
[N(CH3)3(CH2OH)]+
Data
DOIs
Optimisation: DOI:10042/26270
Frequency Analysis:DOI:10042/26271
Population Analysis:DOI:10042/26272
Summary of results
| Calculation | Optimisation using 6-31G(d,p) | Frequency Analysis | Population Analysis |
|---|---|---|---|
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FREQ | SP |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 | 1 |
| Spin | Singlet | Singlet | Singlet |
| E(RB3LYP) | -289.39470724 a.u. | -289.39470724 a.u. | -289.39471219 a.u. |
| RMS Gradient Norm | 0.00000048 a.u. | 0.00000053 a.u. | - |
| Dipole Moment | 2.1357 Debye | 2.1357 Debye | 2.1356 Debye |
| Point Group | C1 | C1 | C1 |
| Job cpu time | 0 days 0 hours 29 minutes 13.0 seconds | 0 days 0 hours 24 minutes 6.7 seconds | 0 days 0 hours 1 minutes 1.4 seconds |
Final sets of forces and displacements for optimisation using 6-31G(d,p)
Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000015 0.000060 YES
RMS Displacement 0.000004 0.000040 YES
Predicted change in Energy=-7.863587D-12
Optimization completed.
-- Stationary point found.
Final sets of forces and displacements for frequency analysis
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000066 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-1.186848D-11
Optimization completed.
-- Stationary point found.
Low frequencies
Low frequencies --- -8.4541 -5.0324 -1.1157 -0.0009 -0.0009 -0.0008 Low frequencies --- 131.1059 213.4594 255.7116
Optimisation was performed using the basis set 6-31G(d,p). The RMS gradient norm is <0.001 and close to 0 for both. In addition, all calculations also converged. The 6 low frequencies (first line) are also within the required range of +/-15cm-1. In addition, the second set of frequencies have positive values, indicating minimum energies. All 3 calculations have similar dipole moments. It can be observed that the energy from the population analysis is slightly different from that of the optimisation and frequency analysis. However, as previously advised, the calculation was left alone since the optmised molecule was used for population analysis.
[N(CH3)3(CH2CN)]+
Data
DOIs
Optimisation: DOI:10042/26210
Frequency Analysis:DOI:10042/26211
Population Analysis:DOI:10042/26212
Summary of results
| Calculation | Optimisation using 6-31G(d,p) | Frequency Analysis | Population Analysis |
|---|---|---|---|
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FREQ | SP |
| Calculation Method | RB3LYP | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) | 6-31G(d,p) |
| Charge | 1 | 1 | 1 |
| Spin | Singlet | Singlet | Singlet |
| E(RB3LYP) | -306.39376383 a.u. | -306.39376383 a.u. | -306.39377031 a.u. |
| RMS Gradient Norm | 0.00000040 a.u. | 0.00000053 a.u. | - |
| Dipole Moment | 5.7642 Debye | 5.7642 Debye | 5.7640 Debye |
| Point Group | C1 | C1 | C1 |
| Job cpu time | 0 days 0 hours 23 minutes 35.6 seconds | 0 days 0 hours 26 minutes 37.3 seconds | 0 days 0 hours 1 minutes 21.4 seconds. |
Final sets of forces and displacements for optimisation using 6-31G(d,p)
Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000040 0.000060 YES
RMS Displacement 0.000007 0.000040 YES
Predicted change in Energy=-9.002465D-12
Optimization completed.
-- Stationary point found.
Final sets of forces and displacements for frequency analysis
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000074 0.001800 YES
RMS Displacement 0.000020 0.001200 YES
Predicted change in Energy=-3.467927D-11
Optimization completed.
-- Stationary point found.
Low frequencies
Low frequencies --- -2.5807 -0.0009 -0.0007 -0.0004 7.1537 9.6772 Low frequencies --- 91.7766 154.0307 210.9339
Optimisation was performed using the basis set 6-31G(d,p). The RMS gradient norm is <0.001 and close to 0 for both. In addition, all calculations also converged. The 6 low frequencies (first line) are also within the required range of +/-30cm-1. In addition, the second set of frequencies have positive values, indicating minimum energies. All 3 calculations have similar dipole moments. Once again, it can be observed that the energy from the population analysis is slightly different from that of the optimisation and frequency analysis. However, as previously advised, the calculation was left alone since the optmised molecule was used for population analysis.
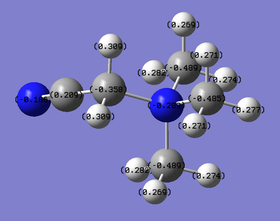
Comparison of charge distribution on [N(CH3)4]+, [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+
The charge range has been set to -0.725 to 0.725 for proper comparison. Red represents negative charge where the more negative it is, the lighter the red colour. Similarly, green represent positive charge where the more positive it is, the lighter the green colour. The effect on the charge distribution with a change in functional groups can be seen by observing the difference in charge distributions when comparing [N(CH3)4]+, [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+. -OH is an electron donating group (EDG) while -CN is an electron withdrawing group (EWG).
At first glance, by replacing one H atom on -CH3 to -OH, the charge on the central N atom became more negatively charged while doing so with -CN lead a less negatively charge N atom. This is because -OH is an EDG that can donate electron density to the central N atom due to the lone pairs on O. Similarly, -CN draws the electron density away from the central N atom, hence making it less negative.
It can also be observed that the C atoms on the non-substituted methyl groups are not significantly affected by the change in functional group, with their charge values only slightly more negative (ranging from -0.485 to -0.494 than that found in [N(CH3)4]+ (-0.483). In addition, the C atoms now have varying charge values as the overall structure is no longer symmetrical with a proper tetrahedral structure. Hence the charge distribution will vary a little. This is confirmed by looking at the N-C bond lengths where the N-COH (1.53Å) and N-CN (1.55Å) bonds are both longer than the N-CH3 (1.50-1.51Å).
The effect of -OH as an EDG can be observed by looking at the charge value of the C atom attached to it. Unlike the other C atoms, this particular C atom has a positive charge value of 0.088. This seems unexpected as -OH is expected to donate more electron density and the C atom should have an even more negative charge value. However, O is a highly electronegative atom and will be expected to withdraw electron density from its surrounding atoms. As a result, it has a charge value of -0.725. In additional, this causes the hydroxyl H atom to be highly electropositive (+0.521) when compared to the H atoms found on the methyl groups (+0.269 to +0.282). The H atoms of the methyl groups have similar charge values to those found in [N(CH3)4]+. The H atoms in -CH2OH are found to be slightly less electropositive than usual. This indicates that they are also affected by the electron-donating ability of the -OH group, which donates electron density through the C-N frame work.
When looking at [N(CH3)3(CH2CN)]+, it can once again be observed that the C atoms of the methyl groups are not significantly affected by the electron withdrawing effect of the -CN group, as their charge values range from -0.485 to -0.489. This also applies for the H atoms in the methyl group which have similar charge values to those found in [N(CH3)4]+. However, it can be seen that the C atom next to the -CN group has its electron density withdrawn as it now has a less negative charge value of -0.358 when compared to the rest. In the -CN functional group, it can be observed that the electronegative N atom is withdrawing electron density as the charge on the C atom is positive with a value of 0.209. This is a significant difference from the C atoms in the methyl groups which are also attached to a N atom. This is because the CN is triply bonded. Similarly, due to the electron withdrawing effect of the -CN group, the H atoms in -CH2CN are found to be slightly more electropositive than usual.
Overall, the charges all sum up to 1 for all the ions.
HOMO and LUMO of [N(CH3)4]+, [N(CH3)3(CH2OH)]+ and [N(CH3)3(CH2CN)]+
Shape of HOMOs
In the HOMO of [N(CH3)4]+, 2 H atoms in 2 methyl groups (Atoms #6, #8, #11, #12) are not involved, while 1 H atom in each of the remaining methyl groups are also not involved (Atoms #4 and #16). There are a total of 5 planar nodes, found at the C atoms and the N atom. For the methyl groups with only 1 H atom involved, the p orbital of the C atom overlaps in phase with the s atomic orbital of the H atom while the other phase overlaps in phase with the p orbital of the N atom. For the methyl groups with 2 H atoms involved, 1 H atom overlaps in phase with the p orbital of the C atom while the other H atom overlaps in phase with the opposite phase of the same p orbital. There is strong through space in phase interactions between the same phase orbitals formed from the overlap mentioned above.
In the HOMO of [N(CH3)3(CH2OH)]+, less atoms (Atoms H#5, H#6, H#7, H#9, H#11, H#13, H#14 not involved) are involved and the orbitals are concentrated at the -OH region. In 2 of the methyl groups, only 1 H atom is involved, and the s orbitals overlap in-phase with the p orbitals of the C atoms. The other phase of all 3 p orbitals of the C atoms in the methyl groups then overlap in phase with the p orbital of the N atom. The other phase of the p orbital overlaps in phase with the p orbital of the C atom beside the -OH group. The remaining phase of this C orbital overlaps with one of the H atoms it is attached to. The lone pair in the p orbital of the O in -OH is also involved in the HOMO. Overall there is a change in the shape of the HOMO in the presence of the -OH group as it is no longer symmetrical in shape. The donation of electron density to N atom from the -OH has resulted in larger orbital seen. Also, the p orbital of O that contains the lone pair show is large, such that it surrounds the hydroxyl H atom without interacting with it, hence indicative of the large amount of electron density at -OH.
In the HOMO of [N(CH3)3(CH2CN)]+, even less atoms are now involved. The HOMO is highly concentrated on the C-CN fragment of the ion. The p orbitals of C and N on -CN overlap in phase and there out-of-phase interaction with the p orbital on N. This results in a greater change in shape of the HOMO as it is now localised at CN. Due to the electron withdrawing effect of the -CN group, the HOMO does not involve the methyl groups.
Shape of LUMOs
In the LUMO of [N(CH3)4]+, the p orbitals of the C atoms in the methyl group overlap in phase for one of the phase. This overlap is strong and large as the orbital formed is highly delocalised. In the core of the ion lies the s orbital of the N, which is of opposite phase to the large orbital formed by the p orbitals of the C atoms and there is strong out-of-phase interaction between the 2. Similarly, there is also strong out of phase interaction with the opposite phases of the p orbitals on C. Overall the shape of the LUMO is symmetrical.
In the LUMO of [N(CH3)3(CH2OH)]+, similar interactions are seen in the methyl groups with the N atom. However, there is now in-phase overlap of the s orbital of the N atom with the s orbital of the C atom that is right next to the -OH group. This overlap also involves the sp3 orbital containing the lone pair in O. The H atoms of the CH2 OH fragment are also involved in in-phase overlap with the methyl groups. The shape of the LUMO is no longer symmetrical, because of the different types of orbital overlaps involved with the -OH group.
In the LUMO of [N(CH3)3(CH2CN)]+, the p orbital of the C atom beside the -CN group now overlaps in phase with the p orbital of the C atom in the -CN group. This orbital has out of phase interactions (anti-bonding) with the p orbital of the N atom in the -CN group. In addition, due to the electron withdrawing effect of the -CN group, the H atoms of the methyl groups are no longer involved in the LUMO has their electron density has been withdrawn. This reduces the size of the orbital formed from the favourable overlap of the p orbitals of the C atoms in the methyl groups. As a result, the shape of the LUMO is also no longer symmetrical.
Energies of HOMOs and LUMOs
In the presence of the functional groups, the energies of the HOMO and LUMO has shifted. The HOMO of the [N(CH3)3(CH2OH)]+ is found to be the least stable, followed by [N(CH3)3(CH2CN)]+ and [N(CH3)4]+. This is due to a reduction of the bonding interactions and an increase in anti-bonding interactions in the HOMOs in the presence of the different functional groups. In general, having an EDG will increase the energyl level while having an EWG will decrease the energy level. However, the comparison is weak, as the HOMO of [N(CH3)3(CH2CN)]+ no longer involves the methyl groups due to the electron withdrawing effect of the -CN group. For the LUMOs, the stability of the LUMOs decrease from [N(CH3)3(CH2CN)] > [N(CH3)4]+ > [N(CH3)3(CH2OH)]+ . Once again, this is due to the balance of the amount of bonding interactions and anti-bonding interactions in the LUMOs.
The HOMO-LUMO gaps of the ions are affected by the change in energies caused by the influenced of the functional groups. The trend shows a decrease in the HOMO-LUMO gap [N(CH3)4]+ > [N(CH3)3(CH2OH)]+ > [N(CH3)3(CH2CN)]+. The difference in energy gap can be observed experimentally by collection absorption spectrum of the cations as they will show peaks at different wavelength.
The energies of the HOMOs and LUMOs can affect the ability of the cations in interaction with other molecules. HOMOs are often seen as donor orbitals as they are the highest energy orbitals that contain electrons while LUMOs are often seen as acceptor orbitals as they are the most stable orbitals that do not contain any electrons. Hence the energy levels of the HOMOs and LUMOs can affect the nucleophilicity and electrophilicity of the ions. If we compare the energies of the 3 cations, the best donor orbital is the HOMO of [N(CH3)3(CH2OH)]+ as it is the least stable and will be the most reactive. In addition, the best acceptor orbital is the LUMO of [N(CH3)3(CH2CN)]+ as it is the most stable. However, whether the interaction is strong or weak is dependent on the energy levels of the HOMO or LUMO of the molecule the cation is interacting with. The best overlap comes when there is a small energy gap between the respective HOMO and LUMO involved in interaction.
Conclusion
The calculations made were complete and accurate as they converged. When frequency analysis was performed, steps were taken to ensure that all the low frequencies values were within the required range of +/-30cm-1. Comparisons between calculated results were made based on those produced from the same method and basis set in order to ensure accuracy. Energy differences were ignored as the optimised molecules obtained from using the basis set 6-31G(d, p) were used for frequency analysis and population analysis. Overall, the calculations helped to explore the geometries of the 'onium' ions by looking at the key bond lengths and angles; observe the charge distribution in the ions and compare the influences of placing electron withdrawing and electron donating groups on the ions.
References
- ↑ J. F. Lehmann and G. J. Schrobilgen, Journal of the American Chemistry Society, 2005, 127, 9416–9427.DOI:10.1021/ja0402607
- ↑ G. Stringer, N. J. Taylor, and T. B. Marder, Acta Crystallographica , 1996, C52, 80–82.DOI:10.1107/S0108270195010304
- ↑ D. R. Lide, CRC Handbook of Chemistry and Physics, 89th Edition (Internet Version 2009), CRC Press/Taylor and Francis, Florida, 89th edn., 2009.
- ↑ P. Atkins, T. Overton, J. Rourke, M. Weller, and F. Armstrong, Inorganic Chemistry, Oxford University Press, Oxford, 5th edn., 2010.