Rep:Mod:qwt11 inorg

Qian Wen Tan
CID: 00700342

Optimisation of BH₃ molecule

Optimisation was performed on 2 different BH₃ molecules. The B-H bond lengths for the first(A) were not modified while the bond lengths for the second(B) were modified to 1.53Å, 1.54Å and 1.55Å.

Using basis set 3-21G

Log file
A:[| 3-21G .log file for (A)]
B:[| 3-21G .log file for (B)]

Summary of results
BH₃ optimisation

BH₃ molecules	(A)	(B)
File Type	.log	.log
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	3-21G	3-21G
Charge	0	0
Spin	Singlet	Singlet
E(RB3LYP)	-26.46226433 a.u.	-26.46226429 a.u.
RMS Gradient Norm	0.00004507 a.u.	0.00008851 a.u.
Dipole Moment	0.0000 Debye	0.0003 Debye
Point Group	D_3h	CS
Job cpu time	0 days 0 hours 0 minutes 6.0 seconds	0 days 0 hours 0 minutes 12.0 seconds

Final sets of forces and displacements for (A)

   Item               Value     Threshold  Converged?
 Maximum Force            0.000090     0.000450     YES
 RMS     Force            0.000059     0.000300     YES
 Maximum Displacement     0.000352     0.001800     YES
 RMS     Displacement     0.000230     0.001200     YES
 Predicted change in Energy=-4.580958D-08
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for (B)

 Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000940     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672478D-07
 Optimization completed.
    -- Stationary point found.

Optimisation was performed on 2 different starting BH₃ molecules using the basis set 3-21G. as they give different results. The RMS gradient norm is <0.001 and close to 0 for both. In addition, both calculations also converged. Since the most basic basis set was used, the point group of (B) is CS instead of the expected D_3h. This indicates that the level of calculation is insufficient for the programme to come up with the correct point group. The energy is calculated to be -26.46226433 a.u. for (A) and -26.46226429 a.u. for (B). The difference in energy is negligible.

Using basis set 6-31G(d,p)

Log file
A:[| 6-31G(d,p) .log file for (A)]
B:[| 6-31G(d,p) .log file for (B)]

Summary of results
BH₃ optimisation

BH₃ molecules	(A)	(B)
File Type	.log	.log
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)
Charge	0	0
Spin	Singlet	Singlet
E(RB3LYP)	-26.61532363 a.u.	-26.61532358 a.u.
RMS Gradient Norm	0.00000475 a.u.	0.00008206 a.u.
Dipole Moment	0.0000 Debye	0.0003 Debye
Point Group	D_3h	CS
Job cpu time	0 days 0 hours 0 minutes 6.0 seconds	0 days 0 hours 0 minutes 15.0 seconds

Final sets of forces and displacements for (A)

   Item               Value     Threshold  Converged?
 Maximum Force            0.000009     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000038     0.001800     YES
 RMS     Displacement     0.000025     0.001200     YES
 Predicted change in Energy=-5.342731D-10
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for (B)

 Item               Value     Threshold  Converged?
 Maximum Force            0.000204     0.000450     YES
 RMS     Force            0.000099     0.000300     YES
 Maximum Displacement     0.000875     0.001800     YES
 RMS     Displacement     0.000418     0.001200     YES
 Predicted change in Energy=-1.452109D-07
 Optimization completed.
    -- Stationary point found.

Optimised length
B-H: 1.19Å

Optimised angle
H-B-H: 120.0^o

Optimisation of BH₃ was performed using the basis set 6-31G(d,p), which is more accurate than 3-21G. The RMS gradient norm is <0.001 and close to 0 for both. In addition, both calculations also converged. The energy is calculated to be -26.61532363 a.u. for (A) and -26.61532358 a.u. for (B). Once again, the slight difference in energy is negligible. The optimised length of 1.19Å is identical to the one reported in literature^[1], indicating accuracy in the calculation. One important observation is that the point group of (B) remained as CS despite using the basis set 6-31G(d,p). This implies that the programme was unable to detect the correct point group of the molecule as this is considered to be a low level calculation. This will later affect the frequency analysis of BH₃ as shown below.

Optimisation of GaBr₃ molecule

DOI
DOI:10042/26068

Summary of results

GaBr₃ optimisation

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.69989295 a.u.
RMS Gradient Norm	0.00402846 a.u.
Dipole Moment	0.0000 Debye
Point Group	D₃h
Job cpu time	0 days 0 hours 0 minutes 23.1 seconds

Final sets of forces and displacements

   Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282688D-12
 Optimization completed.
    -- Stationary point found.

Optimised length
Ga-Br: 2.39Å

Optimised angle
Br-Ga-Br: 120.0^o

Optimisation of GaBr₃ was performed using the basis set LANL2DZ as Ga and Br are heavy atoms that require the use of pseudo-potentials for more accurate calculations. The RMS gradient norm is <0.001 and close to 0 and the calculation converged. The energy is calculated to be -41.69989295 a.u.. The reported Ga-Br bond length for GaBr₃ is 2.249Å^[1]. This is slightly shorter than the computed length but the difference is not significant. Overall, the computed length of 2.39Å is reasonable.

Optimisation of BBr₃ molecule

The BBr₃ molecule was created by modifying BH₃ (A).
Log file
[|Gen .log file]

Summary of results
BBr₃ optimisation

File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Charge	0
Spin	Singlet
E(RB3LYP)	-64.43645296 a.u.
RMS Gradient Norm	0.00000382 a.u.
Dipole Moment	0.0000 Debye
Point Group	D_3h
Job cpu time	0 days 0 hours 0 minutes 40.5 seconds

Final sets of forces and displacements

Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027258D-10
 Optimization completed.
    -- Stationary point found.

Optimised length
B-Br: 1.93Å

Optimised angle
Br-B-Br: 120.0^o

Optimisation of BBr₃ was performed using the basis set Gen as B is a light atom while Br is a heavy atom. This allows the specification of basis sets for the individual atoms. The RMS gradient norm is <0.001 and close to 0 and the calculation converged. The energy is calculated to be -64.43645296 a.u.. Comparing the optimised B-Br length to the reported length of 1.893Å^[1], it is slightly longer but still close enough.

Analysis of results

Comparison of bond lengths of BH₃, BBr₃, and GaBr₃

Molecules	BH₃	BBr₃	GaBr₃
Optimised Bond lengths (Å)	1.19	1.93	2.39

Table 1: Bond lengths of BH₃, BBr₃, and GaBr₃

The bond lengths increases from BH₃ to BBr₃ to GaBr₃. It reflects the bond strength, for the longer the bond, the weaker it is. In turn, bond strength is affected by a few factors: (1) size of atoms, (2) difference in electronegativity between atoms, (3) extent of orbital overlap between atoms and (4) bond polarity.

By comparing BH₃ and BBr₃, it can be observed that changing from a small ligand (H) to a large ligand (Br) lead to an increase in the bond length. Both B-H and B-Br are covalent bonds. The increase in bond length is caused by a few factors. Firstly, the Br atom will naturally be displaced further from B than the H atom as it is bigger in size. This is due to greater electron-electron repulsion when the two atoms are side by side as Br atom has more electrons. Hence, the equilibrium length will be longer between B-Br than B-H. In addition, the bond length is also affected by the difference in electronegativity between B and H and B and Br. H and Br are both more electronegative than B but Br is significantly more electronegative than H. Hence, the B-Br bond is more polar than the B-H bond as the more electronegative Br will draw more electrons towards it than H. This is a result of greater polarisability of Br than H. As a result, there is a significant increase in bond length from 1.19Å to 1.93Å.

GaBr₃ has a longer bond length than BBr₃. In general, Ga is a bigger molecule with more electrons than B hence the bond length will increase as mentioned before. In addition, although both Ga and B belong to group 13 of the Period Table of Elements, Ga is a metal while B is a non-metal. Hence, the Ga-Br bond is ionic while the B-Br bond is covalent. In general, ionic bonds are weaker than covalent bonds as there are electrostatic attraction between the ions while a covalent bond involves the 2 atoms sharing their electrons. In addition, the larger the atom, the more diffused its orbital. Hence, Ga-Br bond is the weakest as it has the least orbital overlap while the B-H bond is the strongest as it has the most orbital overlap.

A bond is an attractive interaction between atoms. According to the nature of interaction and the type of atoms involved, there are a few different types of bonds possible: covalent bond, ionic bond, metallic bond and agostic bond. All these forms of bond result in the formation of chemical molecules constructed from 2 or more atoms. In addition, there is also hydrogen bond, which is technically not a proper bond, but it is also formed due to attractive interactions between atoms. Overall, the formation of a bond will lead to a reduction in the overall energy of the system.

In some structures, Gaussview does not show the expected bonds. However this does not imply the absence of a bond. Rather, Gaussview has been structured to show the presence of a bond, if the distance between the 2 atoms is within a pre-defined value. Hence, as long as the bond distance between atoms is out of this value, Gaussview will not draw in the bond. However, this does not define the presence of the bond, as it is still dependent on the interaction between the atoms; if it is sufficiently strong, a bond will still be formed.

Frequency analysis for BH₃

Log file
[| Frequency analysis .log file for (A)]
[| Frequency analysis .log file for (B)]
[| Frequency analysis .log file for (B)(int=ultrafine scf(conver=9))]

Summary of results
BH₃ optimisation

BH₃ molecules	(A)	(B)	(B)(int=ultrafine scf(conver=9))
File Type	.log	.log	.log
Calculation Type	FREQ	FREQ	FREQ
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)
Charge	0	0	0
Spin	Singlet	Singlet	Singlet
E(RB3LYP)	-26.61532363 a.u.	-26.61532358 a.u.	-26.61532349 a.u.
RMS Gradient Norm	0.00000477 a.u.	0.00008202 a.u.	0.00008330 a.u.
Dipole Moment	0.0000 Debye	0.0003 Debye	0.0003 Debye
Point Group	D_3h	CS	CS
Job cpu time	0 days 0 hours 0 minutes 5.0 seconds	0 days 0 hours 0 minutes 15.0 seconds	0 days 0 hours 0 minutes 7.0 seconds

Final sets of forces and displacements for (A)

         Item               Value     Threshold  Converged?
 Maximum Force            0.000010     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000038     0.001800     YES
 RMS     Displacement     0.000019     0.001200     YES
 Predicted change in Energy=-5.368813D-10
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for (B)

  Item               Value     Threshold  Converged?
 Maximum Force            0.000189     0.000450     YES
 RMS     Force            0.000082     0.000300     YES
 Maximum Displacement     0.000784     0.001800     YES
 RMS     Displacement     0.000317     0.001200     YES
 Predicted change in Energy=-1.380433D-07
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for (B)(int=ultrafine scf(conver=9))

 Item               Value     Threshold  Converged?
 Maximum Force            0.000207     0.000450     YES
 RMS     Force            0.000100     0.000300     YES
 Maximum Displacement     0.000753     0.001800     YES
 RMS     Displacement     0.000403     0.001200     YES
 Predicted change in Energy=-1.411213D-07
 Optimization completed.
    -- Stationary point found.

Frequencies for (A)

Low frequencies --- -3.5991 -1.1355 -0.0054 1.3745 9.7046 9.7707
Low frequencies --- 1162.9825 1213.1733 1213.1760

Frequencies for (B)

Low frequencies --- -0.0008 -0.0004 0.0008 33.8606 41.5990 43.7038
Low frequencies --- 1163.5023 1213.4686 1213.5878

Frequencies for (B)(int=ultrafine scf(conver=9))

Low frequencies --- -0.0008 -0.0004 0.0009 28.8837 40.2093 44.9269
Low frequencies --- 1163.4954 1213.3988 1213.6046

Frequency analysis was performed on (A) and (B). The RMS gradient norm is <0.001 and close to 0 for all and all the calculations converged. Although we were instructed to work with (B), which has it's bond lengths modified, frequency analysis indicated that the low frequencies fall out of the required range of +/- 15cm^-1. This is observed even after using the keyword 'int=ultrafine scf(conver=9)' and checking the box for tight convergence criteria. As a result, the remaining analysis data were taken from (A) as advised by the demonstrator. It can be observed that the calculated energy, dipole moment and point group are identical to the one calculated before, indicating that the same molecule was used.

Table of vibrations

#	Forms of vibration	Frequency (cm^-1)	Intensity	Symmetry (D_3h point group)
1	All the H atoms move in and out of the plane together while the B atom also moves in and out of plane but in opposite direction to the H atoms.	1163	92.5497	A2"
2	The 2 bottom H atoms are scissoring while the top H atom and the B atom moves up and down due to the motion.	1213	14.0545	E'
3	The top H atom performs alternate in-plane scissoring with the bottom 2 H atoms while the B atom remains stationary. The 2 bottom H atoms are rocking in plane.	1213	14.0581	E'
4	All 3 H atoms move inward and outward in the plane (symmetric stretching), from the center while the B atom remains stationary.	2582	0.0000	A1'
5	The 2 bottom H atoms perform asymmetric stretching while the top H atom remains stationary. The B atom moves slightly left and right in plane.	2716	126.3285	E'
6	The 2 bottom H atoms perform symmetric stretching while the top H atom performs asymmetric stretching. The B atom moves slightly up and down in plane.	2716	126.3189	E'

Table 2: Vibrational frequencies and modes of BH₃

IR spectrum

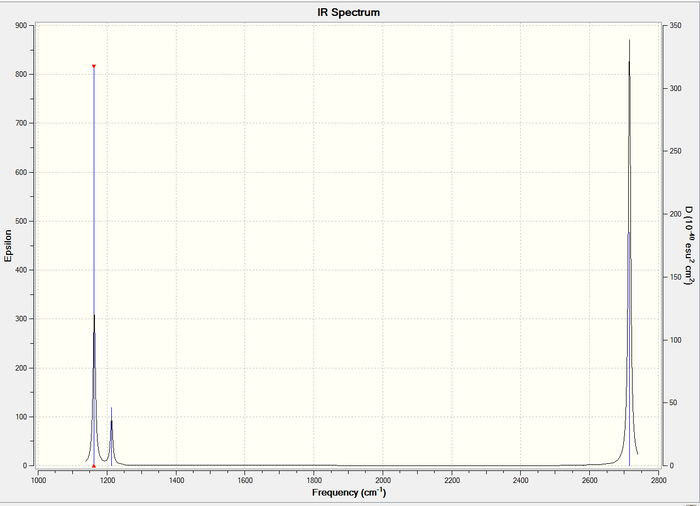
Figure 1: IR spectrum of BH₃

For the BH₃ molecule, there are a total of 3N-6 = 6, where N = 4, vibration modes observed as seen in the Table above. However, the IR spectrum only shows 3 peaks. This is due to two reasons. Firstly, vibration mode #4 is not observed as it does not result in a change in dipole moment. Hence the intensity as seen in Table 2 is 0.0000. Vibrational modes #2 and #3 have the frequency value of 1213cm^-1. As a result, the individual peaks will overlap to give a single peak. This is similarly observed for vibrational modes #5 and #6, in which both have a frequency of 2716cm^-1. Hence, only 3 peaks will be observed in the IR spectrum.

Frequency analysis for GaBr₃

DOI file
DOI:10042/26117

Summary of results
GaBr₃ frequency analysis

File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.70082783 a.u.
RMS Gradient Norm	0.00000011 a.u.
Dipole Moment	0.0000 Debye
Point Group	D_3h
Job cpu time	0 days 0 hours 0 minutes 16.3 seconds

Final sets of forces and displacements

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-6.142862D-13
 Optimization completed.
    -- Stationary point found.

Frequencies

Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010
Low frequencies --- 76.3744 76.3753 99.6982

Table of vibrations

#	Forms of vibration	Frequency (cm^-1)	Intensity	Symmetry (D_3h point group)
1	2 of the Br atoms and the Ga atom are moving left and right in plane while the last Br atom is moving in opposite direction (right then left). These are in-plane rocking and scissoring bending modes.	76	3.3447	E'
2	The 2 bottom Br atoms are moving down and up(scissoring) while the top Br atom and Ga atom are moving up and down (opposite direction).	76	3.3447	E'
3	All 3 Br atoms move in and out of the plane. The Ga atom does the same but in opposite direction.	100	9.2161	A2"
4	The 3 Br atoms stretches symmetrically in plane while the Ga atom remains stationary.	197	0.0000	A1'
5	The 2 bottom Br atoms perform asymmetric stretching while the Ga atom moves left and right in plane. The last Br atom remains stationary.	316	57.0704	E'
6	All 3 Br atoms move up and down while the Ga atom moves in opposite direction (down then up).	316	57.0746	E'

Table 3: Vibrational frequencies and modes of GaBr₃

IR spectrum

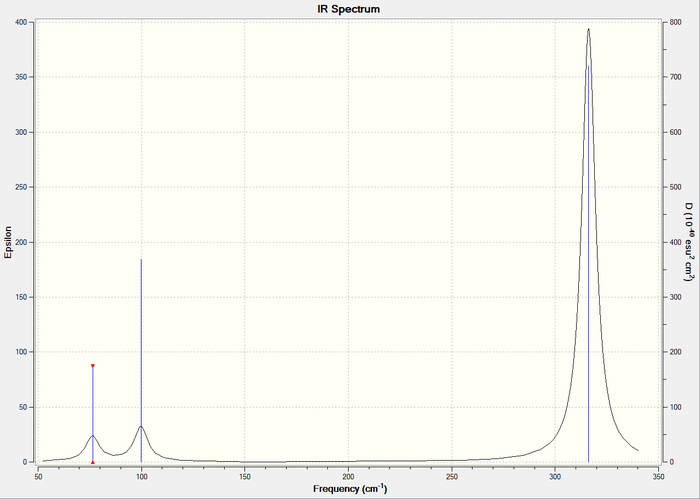
Figure 2: IR spectrum of GaBr₃

Frequency analysis was performed on GaBr₃ using the pseudo-potential LANL2DZ. The RMS gradient norm is <0.001 and close to 0 for both. In addition, the calculation converged. Looking at the energy, dipole moment and point group, they are identical to the ones calculated above, indicating that the same molecule was used. The 6 low frequencies (first line) are also within the required range of +/-15cm^-1, hence there is accuracy in the calculation. The lowest 'real' vibrational mode is 76cm^-1 and it is when the molecule is in bending modes as shown in the table above.

Frequency analysis comparison between BH₃ and GaBr₃

Table of vibrational modes of BH₃ and GaBr₃

Molecules	Vibrations(cm^-1) /Symmetry	Vibrations(cm^-1) /Symmetry	Vibrations(cm^-1) /Symmetry	Vibrations(cm^-1) /Symmetry	Vibrations(cm^-1) /Symmetry	Vibrations(cm^-1) /Symmetry
BH₃	1163/ A2"	1213/ E'	1213/ E'	2582/ A1'	2716/ E'	2716/ E'
GaBr₃	76/ E'	76/ E'	100/ A2"	197/ A1'	316/ E'	316/ E'

Table 4: Vibrational modes of BH₃ and GaBr₃

The vibrational frequencies are inversely proportional to the reduced mass and proportional to the force constant of the bond. The large difference in the value of frequencies for BH₃ compared to GaBr₃ indicate two things: GaBr₃ has a larger reduced mass than BH₃ and the Ga-Br bond is weaker than B-H bond. This is expected as Ga and Br are much heavier atoms than B and H. In addition, the Ga-Br bond has been calculated and explained to be significantly longer than the B-H bond as mentioned above. Hence, the vibrational frequencies of GaBr₃ are expected to be much smaller than those of BH₃.

Both molecules have a total of 3N-6=6, where N=4, vibrational modes. However, there has been a reordering of the modes as the lowest real mode for BH₃ is at 1163cm^-1 with a A2" symmetry while the same symmetry for GaBr₃ comes after 2 E' symmetry vibrational modes. For BH₃, it involves the movement of 3 light H atoms in and out of the plane as the B atom moves in opposite direction while for GaBr₃ it involves movement of the Ga atom in and out of the plane, in opposite direction to the movement of the Br atoms. Since the Ga and Br are heavier atoms, more energy will be required. Hence the frequency is shifted higher.

Both IR spectra are similar in that they only show 3 peaks despite each molecule having 6 vibrational modes. This is because both molecules have a single vibrational mode that does not result in a change in dipole moment, and hence will not be shown on the IR spectrum. In addition, there are 2 pairs of degenerate vibrational modes for each molecule, causing an overlap of the peaks and resulting in only 3 peaks shown in the spectra. It should also be noted that the peaks for BH₃ are of a greater intensity than those of GaBr₃. This is a result of greater change in dipole moment during the stretching and bending of BH₃ than GaBr₃.

In both spectra, it has been observed that two modes lie fairly closely together, the A2" and E' modes. This is also seen for the A1' and E' modes, but higher in energy. This is because the A1' and E' modes are classified as stretching modes while the A2" and E' are classified as bending modes. The A1' and E; modes require a change in bond length during the stretching, which will result in more energy required. This is because when the bond is stretched, there is deviation from the equilibrium length. When the atoms are too close there will be a repulsion force which needs more energy to overcome during stretching. However, for the A2" and E' modes, bending does not require a change in bond length. The repulsion when the atoms are close in proximity is also lower. Hence, less energy is required.

The same method and basis set for both the optimisation and frequency analysis calculations are used as as a change in the method and basis set will produce different results. The basis sets indicate the level of calculations used for the molecules, and there can be no basis of comparison if different method and basis sets were used for the 2 molecules. This is because their calculations will have different degree of accuracies. This is observed when comparing the energies obtained from optimising BH₃ using 3-21G and 6-31G(d,p)basis sets. The one obtained using 6-31G(d,p) is more accurate.

A frequency analysis produces frequencies which are second derivatives of the potential energy surface. Hence, a positive frequency indicates a minimum while a negative frequency indicates a maximum. As a result, in order to ensure that the energies obtained are minimum, we require a frequency analysis and ensure that the values of the frequencies are all positive when calculated. This will indicate that the structure used for calculation is at its ground state. Similarly, it gives us an indication if the optimisation has failed. This will be observed when a negative frequency is obtained.

Each non-linear molecule has 3N-6 vibrational modes. The 'low frequencies' represent the 6 vibrational modes that are subtracted in the equation. They are small and not counted as part of the vibrational modes as they are simply motions caused by the the centre of mass of the molecule.

Molecular Orbitals of BH₃

DOI file
DOI:10042/26123

Summary of results
BH₃ MO analysis

File Type	.log
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.61532363 a.u.
Dipole Moment	0.0000 Debye
Point Group	D_3h
Job cpu time	0 days 0 hours 1 minutes 33.8 seconds

MO diagram of BH₃

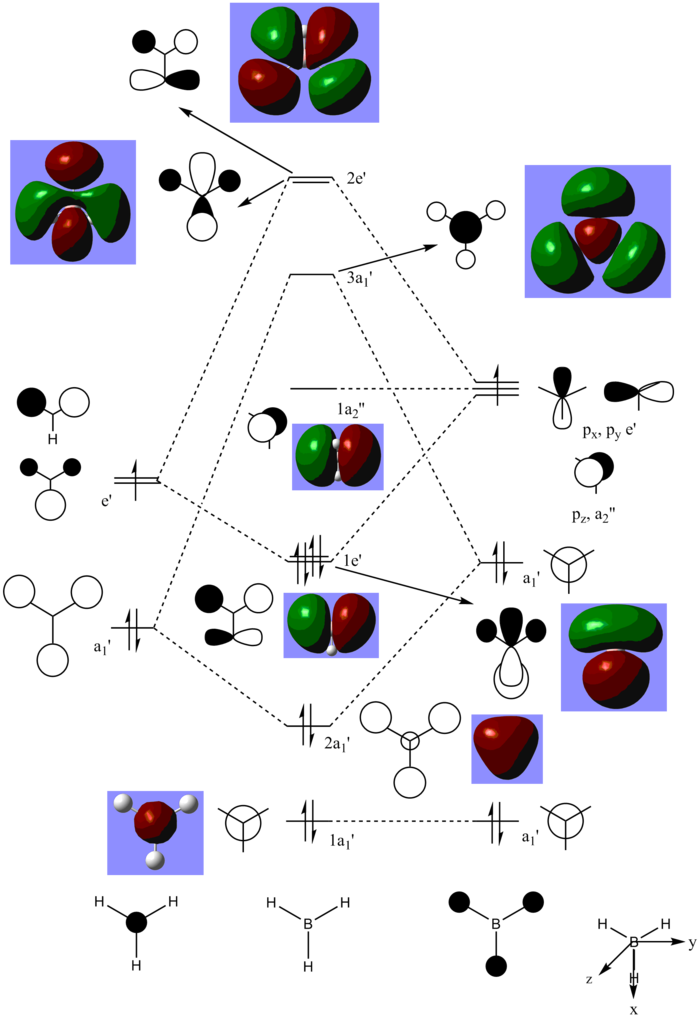
Figure 3: MO diagram of BH₃

Referring to the MO diagram above, there are no significant differences between the real and LCAO MOs. The drawn LCAO MOs are similar to the real MOs produced as BH₃ is a simple molecule with with a straightforward MO diagram. This indicates that qualitative MO theory are sufficiently accurate and useful to show the molecular orbitals of molecules and the distribution of their electron density. However, one has to put caution to such a statement as when the complexity of the molecule increases and mixing occurs between MOs, the qualitative MO theory may fail to provide an accurate view of the MOs.

NBO Analysis of NH₃

Log files
[| 6-31G(d,p) .log file for NH₃]
[| Frequency analysis file for NH₃]
[| Population analysis file for NH₃]
Summary of results

Calculation	Optimisation using 6-31G(d,p)	Frequency Analysis	Population Analysis
File Type	.log	.log	.log
Calculation Type	FOPT	FREQ	SP
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	6-31G(d,p)	6-31G(d,p)	6-31G(d,p)
Charge	0	0	0
Spin	Singlet	Singlet	Singlet
E(RB3LYP)	-56.55776872 a.u.	-56.55776872 a.u.	-56.55776872 a.u.
RMS Gradient Norm	0.00000137 a.u.	0.00000150 a.u.	-
Dipole Moment	1.8465 Debye	1.8465 Debye	1.8465 Debye
Point Group	C₁	C₁	C₁
Job cpu time	0 days 0 hours 0 minutes 12.0 seconds	0 days 0 hours 0 minutes 9.0 seconds	0 days 0 hours 0 minutes 34.3 seconds

Final sets of forces and displacements for optimisation of NH₃ using 6-31G(d,p)

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000002     0.000010     YES
 Maximum Displacement     0.000008     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-1.785252D-11
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for frequency analysis of NH₃

 Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000008     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES
 Predicted change in Energy=-2.196442D-11
 Optimization completed.
    -- Stationary point found.

Frequencies

Low frequencies --- -9.3870 -8.2244 -6.1051 -0.0017 -0.0015 -0.0006
Low frequencies --- 1089.3360 1693.9207 1693.9250

Although the basis set 6-31G(d,p) was used, the point group calculated was C₁ instead of the expected C_3V. This implies that better basis set is still required to ensure greater accuracy in the calculation. In addition, the keyword 'int=9 scf(conver=9)' was used and tight convergence criteria was chosen in order to ensure that the calculations will converge. The RMS gradient norm is <0.001 and close to 0 for both. The energy is calculated to be -56.55776872 a.u. and the dipole moment is calculated to be 1.8465D for the optimisation and the frequency analysis, indicating that the same molecule was used. The low frequencies calculated are also within the required range of +/-15cm^-1. The calculated bond length of 1.02Å is similar to the reported value of 1.012Å^[1].

Charge Distribution

Figure 4: Charge distribution in NH₃ by colour

Figure 5: Labelled charge distribution in NH₃

The charge range for NH₃ is -1.125 to 1.125. Referring to Figure 4, it can be seen that the N atom is negatively charged while the H atoms are positively charged. This is expected as N is more electronegative than H. Figure 5 shows the actual charge values for each atom, -1.125 for N and 0.375 for H. By summing up the charges, we will get a value of 0, which is expected as NH₃ is a neutral molecule. Hence, this indicates accuracy in the calculations.

Association energies: Ammonia-Borane

[| 3-21G file for NH₃BH₃]
[| 6-31G(d,p) .log file for NH₃BH₃]
[| Frequency analysis file for NH₃BH₃]

Summary of results

Calculation	3-21G	6-31G(d,p)	Frequency Analysis using 6-31G(d,p)
File Type	.log	.log	.log
Calculation Type	FOPT	FOPT	FREQ
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	3-21G	6-31G(d,p)	6-31G(d,p)
Charge	0	0	0
Spin	Singlet	Singlet	Singlet
E(RB3LYP)	-82.76661835 a.u.	-83.22468905 a.u.	-83.22468909 a.u.
RMS Gradient Norm	0.00003005 a.u.	0.00000289 a.u.	0.00000475 a.u.
Dipole Moment	5.8431 Debye	5.5645 Debye	5.5645 Debye
Point Group	C₁	C₁	C₁
Job cpu time	0 days 0 hours 0 minutes 21.0 seconds	0 days 0 hours 0 minutes 33.0 seconds	0 days 0 hours 0 minutes 33.0 seconds

Final sets of forces and displacements for optimisation of NH₃BH₃ using 3-21G

 Item               Value     Threshold  Converged?
 Maximum Force            0.000094     0.000450     YES
 RMS     Force            0.000030     0.000300     YES
 Maximum Displacement     0.000419     0.001800     YES
 RMS     Displacement     0.000179     0.001200     YES
 Predicted change in Energy=-5.743898D-08
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for optimisation of NH₃BH₃ using 6-31G(d,p)

         Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000036     0.000060     YES
 RMS     Displacement     0.000012     0.000040     YES
 Predicted change in Energy=-3.124960D-10
 Optimization completed.
    -- Stationary point found.

Final sets of forces and displacements for frequency analysis of NH₃BH₃

Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000041     0.001800     YES
 RMS     Displacement     0.000021     0.001200     YES
 Predicted change in Energy=-3.152412D-10
 Optimization completed.
    -- Stationary point found.

Frequencies

Low frequencies --- -4.9288 -0.0014 -0.0011 -0.0008 2.1989 3.1957
Low frequencies --- 263.3470 632.9566 638.4182

Optimisation was first performed using the basis set 3-21G before using the 6-31G(d,p) basis set on the optimised file as NH₃BH₃ is not a small molecule. The optimised calculation using the 6-31G(d,p) set was done using the keyword 'int=9 scf(conver=9)' and tight convergence criteria was chosen. This was required in order to obtain low frequencies values that are within the +/-15cm^-1 range when frequency analysis was performed. The difference in energies obtained for the 6-31G(d,p) calculation and frequency analysis is negligible.

Bond lengths and angles

Method/Basis set	DFT RB3LYP/6-31G(d,p) (Computed)	HF/ 6-31G (Literature^[2])
B-N bond length/Å	1.67	1.69
B-H bond length/Å	1.21	1.21
N-H bond length/Å	1.02	1.00
N-B-H angle/^o	104.6	104.3
B-N-H angle/^o	111.0	110.9

By comparing the calculated values with the reported values, it can be seen that although the method is different but the basis set is the same, the bond lengths and angles are still close. Hence, the calculations can be predicted to be accurate.

Association & Dissociation Energies
E(NH3)= -56.55776872 a.u.
E(BH3)= -26.61532363 a.u.
E(NH3BH3)= -83.22468905 a.u.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -83.22468905 a.u. -(-56.55776872 a.u.-26.61532363 a.u.) = -0.0515967 a.u. = -135.4671462kJ/mol

Hence, the dissociation energy is 135kJ/mol.

Comparision of energies

Compounds	DFT RB3LYP/6-31G(d,p) (Computed)/a.u.	HF/ 6-31G (Literature^[2])/a.u.
BH₃	-26.61532363	-26.39001
NH₃	-56.55776872	-56.18436
NH₃BH₃	-83.22468905	-82.61182

Using literature values, ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -82.61182 a.u. -(-56.18436 a.u.-26.39001 a.u.) = -0.03745 a.u. = -98.3249825kJ/mol

Hence the literature dissociation energy is 98.3kJ/mol.

It can be observed that there is a deviation of the bond dissociation energy from the literature values. This is because the method used is Hartree-Fock instead of DFT so there is no proper basis for comparison. The use of different methods and basis sets will lead to different computational methods and accuracies, and all these small differences can sum up to a big difference in the final values. The calculations can be repeated to check for accuracy.

Conclusion

In conclusion, the calculations above indicated that using the better basis set, such as 6-31G(d,p) instead of 3-21G will give more accurate results. When frequency analysis was performed, steps were taken to ensure that all the low frequencies values were within the required range of +/-15cm^-1. Comparisons between calculated results were made based on those produced from the same method and basis set in order to ensure accuracy. The energies were checked to ensure that further calculations made were based on the optimised structure found using the 6-31G(d,p) basis set.

References

↑ ^1.0 ^1.1 ^1.2 ^1.3 D. R. Lide, CRC Handbook of Chemistry and Physics, 89th Edition (Internet Version 2009), CRC Press/Taylor and Francis, Florida, 89th edn., 2009.
↑ ^2.0 ^2.1 J. S. Binkley and L. R. Thornel, J. Chem. Phys., 1983, 79, 2932.DOI:10.1063/1.446117

[CRC_Handbook-1] 1.0 ^1.1 ^1.2 ^1.3 D. R. Lide, CRC Handbook of Chemistry and Physics, 89th Edition (Internet Version 2009), CRC Press/Taylor and Francis, Florida, 89th edn., 2009.

[NH3BH3-2] 2.0 ^2.1 J. S. Binkley and L. R. Thornel, J. Chem. Phys., 1983, 79, 2932.DOI:10.1063/1.446117

[1]

[2]

Optimisation of BH3 molecule

Using basis set 3-21G

Using basis set 6-31G(d,p)

Optimisation of GaBr3 molecule

Optimisation of BBr3 molecule

Analysis of results

Frequency analysis for BH3

Frequency analysis for GaBr3

Frequency analysis comparison between BH3 and GaBr3

Molecular Orbitals of BH3

NBO Analysis of NH3

Association energies: Ammonia-Borane

Conclusion

References

Optimisation of BH₃ molecule

Optimisation of GaBr₃ molecule

Optimisation of BBr₃ molecule

Frequency analysis for BH₃

Frequency analysis for GaBr₃

Frequency analysis comparison between BH₃ and GaBr₃

Molecular Orbitals of BH₃

NBO Analysis of NH₃