Rep:Mod:qws123sqw

Modelling MgO: 3rd Year Computational Lab

Introduction

Objectives

The overarching aim of this investigation is to study the thermal expansion of MgO. We aim to calculate the thermal expansion coefficient of MgO and predict its thermal expansion.

We look to use Lattice Dynamics (the Quasi-Harmonic approximation) to compute the vibrational energy levels of MgO in order to investigate the phonon dispersion and vibrational density of states. Furthermore, we look to use Molecular Dynamics to simulate the vibrations as random atomic motions inside a cell.

Our objective is to compare the results from the Quasi-Harmonic Approximation with the results from the Molecular Dynamics simulation.

Systems and Programs in use: DLV and Gulp

For this investigation, the software package DLV (DL Visualise) and the analysis program GULP (General Utility Lattice Program) were used on RedHat Linux software. DLV is a software package commonly used for the construction and visualisation of crystals, surfaces and molecules . In this investigation, we use DLV to construct and visualise cells and vibrations of a crystal of MgO.

GULP is an analytical program frequently used for the simulation of 3D periodic systems. In this investigation, we use GULP for the simulations of MgO using the quasi-harmonic approximation and molecular dynamics. GULP is different from other programs because the simulations it runs are symmetry-adapted. GULP contains many interatomic potentials available to use in its library for two, three or four body systems (ranging from the purely Harmonic approximation to the Ryckaert- Bellemans potential for four bodies).

Theory in Use

Effect of Temperature on systems with Harmonic and Anharmonic Potentials

Figure 1: Effect of temperature with a Harmonic Potential, Picture from: http://people.virginia.edu/~lz2n/mse209/Chapter19.pdf

In the simplest approximation, we can approximate the interatomic (or inter-ionic) potential in MgO to be perfectly harmonic. A harmonic potential is characterised by a restoring force F which is proportional to the displacement of the simple harmonic oscillator from equilibrium (the change in inter-ionic separation from the average value) and pulls the oscillator back towards equilibrium, i.e. where F = -k x (k is the spring constant and x is the displacement from equilibrium). A harmonic potential curve is parabolic (U = (1/2) k x²) and example is shown in Figure 1.

Figure 2: Buckingham Potential Picture from: rimg.geoscienceworld.org

Figure 3: Effect of temperature with a Anharmonic Potential, Picture from: http://people.virginia.edu/~lz2n/mse209/Chapter19.pdf

An increase in temperature would result in a greater vibrational amplitude of the ions (the harmonic oscillators). However, if the inter-ionic potential curves for MgO were perfectly harmonic (if the ions vibrated perfectly harmonically), higher vibration amplitudes would not affect the average inter-ionic separation due to the symmetry of the potential curve (as shown in Figure 1). We would expect higher temperatures to result in larger vibrational amplitudes - but under the purely harmonic approximation, this would have no effect on the average inter-ionic separation (lattice parameter). In other words, for a hypothetical diatomic molecule with exactly harmonic potential, we might expect the atoms to vibrate with greater amplitudes with greater temperature - however, we would expect the mean internuclear separation (the average bond length) to remain constant at all temperatures.

A better approximation for the inter-ionic potential takes anharmonicity into account. A commonly used potential uses Coloumbic potentials (a simple force field for MgO with electrostatic forces between Mg and O ions with 2+ and 2- charges respectively) to account for the long-range potential, and Buckingham repulsive potentials to account for the short-range potential.

The Buckingham potential (V=A exp(-Br) - C/(r^6)) is a simplification of the Lennard-Jones potential, where an exponential term (A exp (-Br)) (where A, B are constants and r is the internuclear separation) is used for the repulsive term instead. The repulsive term takes an exponential form at reasonable distances and accounts for the Pauli repulsion (repulsion between overlapping electron densities), whereas the attractive (r^-6) term (same as LJ) accounts for the dispersion interactions. The Coulombic term is the more dominant term for ionic materials (such as MgO) and can typically contribute up to 90% of the energy. When the Buckingham repulsive potential term is combined with the Coulomb interaction term (as used in this experiment), we obtain a parabola-like overall shape of the total potential curve (as shown in Figure 2) with anharmonic features (e.g. includes possibility of bond-breaking as internuclear separation increases).

Actually, as stated in Figure 3, such anharmonic potential curves are more realistic. It is important to realise that these potential curves are 'asymmetric' - this is key in understanding the physical origin of thermal expansion. As can be seen in Figure 3, this means that as the vibration amplitude increases, we would expect the average inter-ionic separation to increase. Therefore, as we expect vibrational amplitude to increase with temperature, we would thus also expect the lattice parameter to also increase with temperature.

In one part of this investigation, we account for the anharmonic effect of thermal expansion using the quasi-harmonic approximation. Below, we present an introduction into lattice dynamics and the quasi-harmonic approximation.

Lattice Dynamics, Phonons and the Phonon Dispersion Curve

Figure 4: MgO lattice structure, Picture from: www.seas.upenn.edu

The study of lattice dynamics is vital for various applications, ranging from interaction of materials with light, propagation of sound waves in crystals to thermal expansion. In this report, we are concerned with using lattice dynamics to understand the thermal expansion of MgO.

In this investigation, we are concerned with the infinite lattice in a crystal of MgO. To study such a system, we have to make use of infinitely repeated, boundary condition (“supercell”) models, i.e. we consider the system to be made of repeating unit cells.

MgO has a face-centred cubic (fcc) crystal structure (as seen in Figure 4 on the right where we can consider Mg and O ions to be represented by the green and red ions respectively). Therefore, we can take a unit cell of MgO to contain an Mg and an O ion (this is the smallest unit possible that we can use to recreate the macroscopic lattice structure using translation).

Figure 5: Dispersion Curve with Optic and Acoustic Branches, Picture from: http://www.ch.ic.ac.uk/harrison/Teaching/L4_Vibrations.pdf

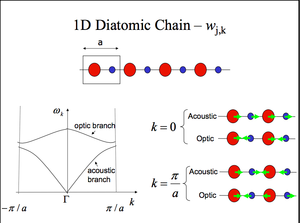
Every lattice vibration has an associated wavelength (λ) and thus a k wave-vector label (k=2π/λ). A dispersion curve relates the frequency of the vibrations (which reflects the associated energy) with the associated k wave-vector labels (k labels are on the x-axis, i.e. we are working in k-space). Branches of continuous energy (frequency) levels in k-space are called ‘bands’ and thus the dispersion curve depicts the band structure. Typically, unit cells containing two or more different types of atoms (or ions) show two types of phonons in a dispersion curve. In Figure 5, we display such an example of a dispersion curve for a lattice where the unit cell contains two different types of atoms. We observe the presence of an acoustic branch and an optic branch.

Acoustic phonons are associated with in-phase motions of atoms/ ions within unit cells. Acoustic phonons can give rise to transverse or longitudinal modes. In the longitudinal mode, vibrations (displacements of individual atoms/ions) is in the same direction as the propagation (dimension along which there is collective excitation of the periodic arrangement of atoms). This is analogous to sound waves in air, which is why the phonon is termed 'acoustic'. In the transverse mode, displacements of atoms is perpendicular to the direction of the propagation. At high wavelengths (low k - values), there is linear relationship between frequency and the k wave-vector. At higher and higher wavelengths (as wavelength tends to infinity and k wave-vector tends to zero) - the frequency of the vibration tends to zero. When wavelength is equal to infinity (k = 0), the vibration corresponds to a displacement of the entire crystal.

Optic phonons are associated with out-of-phase motions of atoms/ ions within unit cells. Optic phonons give rise to longitudinal or transverse transverse modes. In various crystals, these phonons can be excited by electromagnetic radiation, which is why the phonon is termed 'optic'.

Lattice Dynamics: The Quasi-Harmonic Approximation

The partition function of a system (denoted by Z) is determined by summing the Boltzmann factors for all the states of a system: Z (T, N, V … ) = ∑^{all states} exp (-E/ k_BT). The partition function can be used to compute many thermodynamic properties.

In relation to this investigation into the MgO crystal, if we sum over all the phonon wave-vectors (k) and vibrational bands (j), we can computationally calculate thermodynamic properties like the Helmholtz free energy of the crystal. The Helmholtz free energy can be given by the expression:

F = E₀ (a,α,∅) + (1/2) ∑_k,j ħω_k,j + k_BT ∑_k,j ln [1 - exp (-ħω_k,j / k_BT)]

Where: The first term: “E₀ (a,α,∅)” corresponds to the static intermolecular potential energy.

The latter terms: “(1/2) ∑_k,j ħω_k,j + k_BT ∑_k,j ln [1 - exp (-ħω_k,j / k_BT)]” corresponds to the summation of the external modes (we shall see 6 vibrational bands in our dispersion plot of MgO) over the k-points (wave-vectors) in the Brillouin zone.

Of course, such computations will be based on the harmonic approximation, i.e. ions are vibrating harmonically in the crystal with a restoring force proportional to the displacement (F = -kx) which gives rise to acoustic and optic phonons over the entire lattice.

Using only the harmonic approximation, the lattice parameters would be fixed and only affect the Helmholtz free energy F through the static “E₀ (a,α,∅)” term. Thus, we would be unable to investigate and explain the anharmonic property of thermal expansion.

To consider the effects of anharmonicity, we use the quasi-harmonic approximation. In the quasi-harmonic approximation, we determine the vibrational frequencies as if ions were vibrating harmonically for all lattice parameters, but we allow the lattice parameters to vary with temperature to minimise the free energy.

Therefore, we are allowing the phonon frequencies (ω_k,j) to vary with the lattice parameters – we are thus introducing the dependence of the frequencies on volume.

For every given T, GULP computes the internal energy and phonons for various geometries (lattice parameters and molecular orientation) to determine the optimal values of the lattice parameters that cause the free energy to be a minimum. By repeating this for various T values, we should be able to understand the T dependence of the lattice parameters.

Molecular Dynamics

An alternative method we can use for investigating the thermal expansion of MgO is Molecular Dynamics (MD) where we actually directly use an anharmonic potential curve as described above. Unlike the Quasi-Harmonic method (Lattice Dynamics), Molecular Dynamics is completely a classical method (doesn't take phonon theory into account) - i.e. it uses classical physics laws to simulate the evolution of individual atoms/ions in a system over time. The atoms/ions follow classical trajectories responding to forces as per Newton's 2nd Law (F=ma). GULP can then calculate macro properties by computing time averages of the behaviour of individual atoms/ions.

The initial temperature (which affects initial momentum) is set by us. In the simulation, the potential energy is reached by combining the Buckingham repulsive potential and a Coulombic potential (this resultant anharmonic potential curve is discussed in "Effect of Temperature on Harmonic and Anharmonic Potentials"). The force is given by the negative of the derivative of the potential energy curve. The force causes acceleration as per Newton's II (a=F/m) which by definition causes a change in velocity (v_new=v_old + a dt). The updated knowledge of the velocity of the ions is used to update the positions of the atoms after time dt: r_new=r_old + v dt. The value of dt taken is very important. In the computations, we are using equations of constant acceleration - i.e. we are assuming the acceleration is constant over time-frame dt. In reality, the acceleration is constantly changing. We need the dt parameter to be long enough for the calculation to be efficient but short enough so that we can sample all the possible atomic vibrations well. In this experiment, we shall use dt = 1 femtosecond.

Another compromise between accuracy and efficiency must be made when selecting a cell for the MD simulation. The larger the cell size used - the more lattice vibrations we can sample and the expensive the computation. In this investigation, we compromise for a cell containing 32 MgO units (a 32-unit cell).

Figure 6: Mg Phonon Dispersion Curve

Figure 7: Mg Phonon DOS Curve with 1x1x1 Grid

Figure 8: Mg Phonon DOS Curve with 2x2x2 Grid

Figure 9: Mg Phonon DOS Curve with 4x4x4 Grid

Figure 10: Mg Phonon DOS Curve with 8x8x8 Grid

Figure 11: Mg Phonon DOS Curve with 16x16x16 Grid

Figure 12: Mg Phonon DOS Curve with 32x32x32 Grid

Results & Analysis

Using Lattice Dynamics (QHA): Calculating the Phonon Modes of MgO

As aforementioned, a k point in k space labels a particular lattice vibration. GULP and DLV were used to compute the phonon modes of MgO and display the dispersion curve and density of states.

The band structure is now multi-dimensional and it is difficult to to show the frequency of vibrations in 3D k-space. We use GULP to compute and plot frequencies along special directions in reciprocal space (W-L-G-W-X-K). We sets Npoints to 50 - therefore, phonons are computed at 50 points along the special path. The phonon dispersion curve computed is shown in Figure 4. We observe 6 phonon modes (3 acoustic modes that have zero frequency at k = 0, and 3 optic modes).

For each frequency, summing over all the vibrational states will produce the true energy level/ density of states diagram for the infinite MgO crystal. As discussed in the theory, in the quasi-harmonic approximation, the Helmholtz free energy is computed by summing over all the vibrational modes of the crystal. Summing over an infinite grid of k- points would provide the most accurate calculation for the free energy - however such a calculation would also take infinitely long to run! Hence, we look to approximate the total sum as a sum of a finite number of k-points.

DOS curves for various grid sizes were plotted - however, for reference, the DOS curves for grid sizes 1x1x1, 2x2x2, 4x4x4, 8x8x8, 16x16x16, 32x32x32 are shown in Figures 5, 6, 7, 8, 9 and 10 (all computations are conducted on the default temperature 0K and pressure 0GPa).

It is important to reiterate that the DOS curves and phonon dispersion curves computed are inherently related. One realises that the x-axis on the DOS curve (frequency of vibration) is the same as the the y-axis of the phone dispersion curve. Essentially, the DOS curves computed are summing over the vibrational states for a finite number of k-points from the x-axis of the phonon dispersion curve (number of k-points used depends on the grid size).

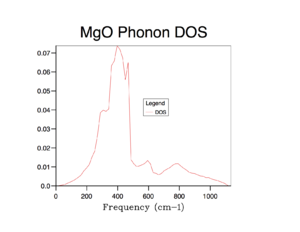
Using the 1x1x1 grid, we have computed the density of states for one k point (as seen in the LogFile for the DOS curve produced by GULP). On the DOS curve for the 1x1x1 grid, we can see that there are peaks at frequencies: 288 cm^-1, 288 cm^-1, 352 cm^-1, 352 cm^-1, 676 cm^-1 and 819 cm^-1(also seen from the Log File). By comparing this data to the phonon dispersion curve, we can see that these are the same frequencies associated with point L.

We see that the peaks at 290 cm^-1 and 350 cm^-1 are double the height of the peaks at 680 cm^-1 and 810 cm^-1. This is because there are twice as many states associated with each of the first two vibrational energy levels (at 290 cm^-1 and 350 cm^-1) than there are at the latter two energy levels (at 680 cm^-1 and 810 cm^-1). We can also understand this by analysing the phonon dispersion curve. We can see that over the entire graph, there are 6 branches (this is because we are considered a motif of two atoms- Mg and O - each of which can move in 3 dimensions in real space). At point L, two branches overlap at 290 cm^-1 and two branches overlap at 350 cm^-1 - i.e. at these two frequencies, we have two degenerate states. Thus there are twice as many vibrational states at these frequencies and this is why the peaks in the DOS curve for these frequencies are twice the size.

As the grid size increases, we take more and more k points into account in our DOS curve. For a 2x2x2 grid, we would consider 8 points - however due to symmetry, we have two sets of 3 degenerate points and thus overall for the 2x2x2 grid, we consider 4 distinct k points (which is confirmed from the LogFile) (This relates to our earlier comment in the theory that the simulations on GULP are symmetry-adapted ). The DOS curves for all 4 single k points are determined and overlapped to give the DOS curve for the 2x2x2 grid.

Thus, in general, more and more vibrations are sampled (i.e. k points are taken into account) in the DOS curve as the grid size increases. As seen from Figures 5, 6, 7, 8, 9 and 10, this has two main effects on the DOS curve:

1) Area underneath the graph: The integral of the entire DOS curve should give us the total number of vibrational states associated with all the k points considered for that DOS curve. As mentioned before, we expect 6 vibrational states to be associated with every k point considered. Thus we would expect 6 vibrational states to be considered for the DOS curve with grid size 1x1x1 and 24 (6 branches x 4 distinct k points) vibrational states to be considered for the DOS curve with grid size 2x2x2 and so forth.

2) Shape: As more and more k points are considered, the DOS curve becomes more and more curved and starts to resemble what we might consider the shape of an ideal DOS curve (if we took an infinite k points into account). We see that as we increase the grid size, more vibrations are sampled and more features appear. It is difficult to say exactly which grid size gives a reasonable approximation for the density of states as this will be subjective (when one considers the DOS curve to resembles density of states closely enough) and what sort of approximation is required. However, in this author's opinion, the DOS curve with a minimum grid size of the 16x16x16 grid gives a reasonable approximation of the DOS curve. The DOS curve of the 16x16x16 grid provides a reasonable picture of the density of states, with the major peak at around 400 cm^-1 and the general shape of the curve (features including smaller peaks in the 500 cm^-1 region) are depicted well. DOS curves with lower grid sizes (e.g. 8x8x8) still have comparatively jagged curves and does not truly full resemble the shape of the density of states. DOS curves with larger grid sizes (e.g. 32x32x32) of course are smoother and represent the shape of the density of states even better - but the improvement compared to the DOS curve with grid size 16x16x16 is not very great. Thus, overall, the grid size of 16x16x16 can be taken as a reasonable approximation of the density of states.

Using Lattice Dynamics (QHA): Computing the Helmholtz Free Energy

Choosing a grid-size to give a reasonable approximation of the Helmholtz free energy can be conducted in a more quantitative manner. Data regarding the calculated Helmholtz free energies for different grid-sizes (integer shrinking factors) and the total CPU time taken for each calculation is shown in the table below.

Table 1: Variation of Helmholtz Free Energy and Computation with Grid-Size Used

Integer Shrinking Factor (Grid Size)	Helmholtz Free-Energy (F) / kJ mol-1	Total CPU time / s
1	-3949.1480	0.0025
2	-3948.7918	0.0034
3	-3948.7767	0.0076
4	-3948.7764	0.0107
8	-3948.7791	0.0818
16	-3948.7796	0.7564
32	-3948.7796	11.5999
64	-3948.7796	449.8641

• Note: Temperature for calculation set to 300K in GULP (and pressure automatically defaults to 0GPa).
• We choose to work in kJ mol^-1 (instead of eV) because the precise values available allow us to study the convergence better.

Table 1 clearly shows us how free energy and computational time vary with grid-size.

We realise that the free energy becomes less negative when we use a grid-size of 2x2x2 instead of 1x1x1. However, this comparison is not directly relevant as the two grid-sizes sample completely different k-labels.

We can choose to use a series of grid-sizes (2x2x2, 4x4x4, 8x8x8, 16x16x16 and 32x32x32) produced by increasing the integer shrinking factor by a factor of 2 every time. In this series, every time we double the shrinking factor, we are sampling more vibrations on top of the vibrations sampled with the previous grid-size. In other words, the DOS curve for grid-size 4x4x4 takes into accounts the k-points sampled in the DOS curve for grid-size 2x2x2 plus some more additional k points. This allows us to understand the convergence a in a systematic manner.

Below, in Table 2, we present the change in Helmholtz free energy every time the shrinking factor is doubled (ΔF represents the value of: current free energy - free energy when the shrinking factor was half the value.

Table 2: Checking Convergence of Helmholtz Free Energy Numerically

Integer Shrinking Factor (Grid Size)	Helmholtz Free-Energy (F) / kJ mol-1	lΔFl / kJ mol-1
2	-3949.7918
4	-3949.7764	0.0154
8	-3949.7791	0.0027
16	-3949.7796	0.0005
32	-3949.7796	0.0001
64	-3949.7796	0.0000

• GULP gives free energy in kJ mol^-1 to 6 decimal places and this number was used to calculate |ΔF|. However, all final reported numerical free energy figures in this report are rounded to 4 decimal places (as this is a reasonable estimate to how precise the computations are).

We observe that free energy becomes less negative when the shrinking factor is increased from 2 to 4, but becomes more negative when the shrinking factor is increased from 4 onwards. However, the absolute value of the change in free energy decreases when the shrinking factor is ncreased. This indicates that as more and more vibrations are sampled, the value of the Helmholtz free energy begins to converge (this is true for all increases in shrinking factors- we have merely used the particular series of shrinking factors selected to demonstrate the point in a systematic manner). This is consistent with our earlier prediction that increasing the shrinking factor will help us obtain more accurate values for free energy. Even though, when increasing the grid-size, some of the values of free energy may be higher than the true value and some may be lower (this just trivially depends on the specific vibrations sampled) - generally, sampling more vibrations provides us with a more accurate value (closer and closer to the converged value).

Going from a grid-size of 32x32x32 to 64x64x64, we observe no change in the calculated free energy (up to 4 decimal places in kJ mol^-1. Therefore, judging by the trend of the value of free energy becoming more accurate with larger shrinking factors, we can approximate the Helmholtz free energy to -3949.7796 kJ mol^-1.

From Table 1, we understand that for calculations accurate to: 1 meV (≈ 0.0965 kJ mol^-1) - i.e. for a value of free energy equal to -3949.7796 0.0965 kJ mol^-1, a grid-size of 2x2x2 is appropriate. We observe that for calculations accurate to: 0.5 meV (≈ 0.0482 kJ mol^-1) , a grid-size of 2x2x2 is also appropriate (as -3949.7918 kJ mol^-1 falls within -3949.7796 ± 0.0482 kJ mol^-1). Similarly, we understand that for calculations accurate 0.1 meV, a grid-size of 3x3x3 is appropriate.

Using the data from Table 1, we can easily appreciate the increase in CPU time required for the computation as we increase the grid-size.

Data from Table 1 supports our earlier hypothesis (in the context of density of states) that a grid-size of 16x16x16 gives us a reasonable approximation for reality. We find that this grid-size gives us a value for Helmholtz free energy that is equal to the value with grid-size 64x64x64 (when both values are rounded to 4 decimal places) and takes a reasonable CPU time of under 1 s for the computation.

Speculation: Optimal Grid-Sizes for CaO, a Zeolite (e.g. Faujasite), a metal (e.g. Li)

The optimal grid-sizes for various different species will depend on their uniquely defined primitive cells in k-space (Brillouin zones)- which directly depends on their unit cells in real space. The smaller the primitive cell is in k-space, the more dense the grid-points sampled are for the same shrinking factor. Therefore, the smaller the primitive cell, the fewer the grid-points (shrinking factor) needed to reasonably approximate calculations. Due to the relationship between k and wavelength (which is based on the lattice constant) as described in the introduction, the larger the unit cell is in real space (the larger the lattice parameter) - the smaller the primitive cell is in k-space.

Therefore, overall, for species with larger lattice parameters in real space, we generally require a smaller optimal grid-size for calculations. CaO has a very similar structure to MgO at low pressures (both have ions with same charges and NaCl-like halite structures at low pressures). CaO has a lattice constant of approximately 4.8 Angstroms as opposed to MgO which has a lattice constant of approximately 4.2 Angstroms . Therefore, we might expect that we could use an even lower grid-size for CaO - however, a grid-size of 16x16x16 would definitely be applicable for this similar species. A zeolite would have a much larger unit cell comprising of several atoms (e.g. faujasite has a lattice constant of approximately 24.6 Angstroms . For this species, a much-lower grid-size could be used for a reasonable approximation. However, again, a grid-size of 16x16x16 would serve well. A pure metal lattice could only have a single atom in the unit cell and we thus might expect metals to have smaller unit cells (e.g. Li metal has a lattice constant of 3.5 Angstroms ). Thus, we may expect metals to require larger grid-sizes to give reasonable approximations and a grid-size of 16x16x16 may not be appropriate.

Effect of Temperature: Quasi-Harmonic Approximation and Molecular Dynamics

Lattice Dynamics- Quasi-Harmonic Approximation Results:

Due to our findings of the reasonableness of using a grid-size of 16x16x16 in our previous investigations, we use this grid-size in our study of the thermal expansion of MgO using the Quasi-Harmonic approximation.

In the introduction, we discussed that under the quasi-harmonic, GULP computes the internal energy and phonons for various geometries (lattice parameters and molecular orientation) for every T to determine the optimal values of the lattice parameters that cause the free energy to be a minimum. We stated that by repeating this for various T values, we should be able to understand the T dependence of the lattice parameters.

Initially, the temperature was varied from 0K to 1000K in steps of 100K. After that, the temperature was raised in steps of 500K to test the relationship between the dependent variables and the temperature under the quasi-harmonic approximation at temperatures closer to the melting point (Melting point of the MgO crystal is 3073 K ). After the computation at 3000K failed, a few more temperatures were tried to determine the highest temperature at which the calculation would work. It was found that GULP was not able to complete the computations above the temperature of 2960K. At temperatures above 2960K, there is a break-down in the quasi-harmonic approximation - the failure to complete the computations implies that the MgO structure is found to be dynamically unstable under the approximation.

Table 3: Lattice Dynamics Data - Change in Free Energy, Lattice Parameter and Volume with Temperature

Figure 13: Unstable Ag structure at higher temperatures

Similar results have been found in other investigations - for example, in a similar experiment, the Ag structure was found to be mechanically unstable at temperatures above 1375K using the quasi-harmonic approximation . This was because, as shown in Figure 13, isotherms (for higher T) do not cross the pressure threshold (P=0) for any value of optimised lattice parameter - i.e. at this pressure and temperature, the structure is not mechanically stable for any lattice parameter. We can infer that we are facing a similar problem working with the quasi-harmonic approximation in our investigation, with GULP being unable to complete any computation for temperatures above 2960K.

Molecular Dynamics Results: In the MD simulation, we use a cell containing 32 MgO units. The temperature range tested mirrors that of the range tested in the lattice dynamics computations. However, in the MD simulation, the MgO crystal structure is found to be stable at all temperatures tested. The time-step was set to 1.0 femtosecond, Equilibration steps was set to 500, Production steps (number of steps run after equilibration was complete) was set to 500, Sampling steps (number of steps over which averages are made) was set to 5 and Trajectory steps was set to 5. The potential model used was of course "ionic.lib" (combination of Coulombic potential and Buckingham repulsive potential).

All values reported are averages values obtained after the last iteration of the simulation.

Table 4: Molecular Dynamics Data - Change in Volume with Temperature

Variation of Free Energy and Lattice Parameter with Temperature under Quasi-Harmonic Approximation (Lattice Dynamics)

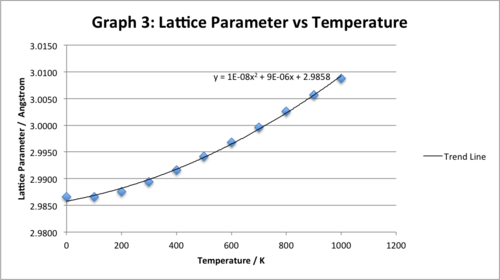
We can use the data collected from the lattice dynamics computations to plot graphs of free energy vs temperature and lattice parameter vs temperature. We first plot the graphs for the temperature range 0K - 1000K and then the graph for the entire range investigated. This is to highlight the data collected for the higher temperatures deviates from the trend in the lower temperature ranges:

Free energy vs Temperature:

Graph for temperature range: 0K-1000K:

We see that the correlation between free energy and temperature is best described with a polynomial relationship. One can observe that all the data points fit carefully with the trend. Free energy decreases with increasing temperature. This happens as per a quadratic relationship (equation for the trend line is shown on the graph) - i.e. free energy decreases (becomes more negative) at a faster rate with increasing temperature. At temperatures higher than 2960K, under the quasi-harmonic approximation, the free energy is extremely high and the system becomes mechanically unstable.

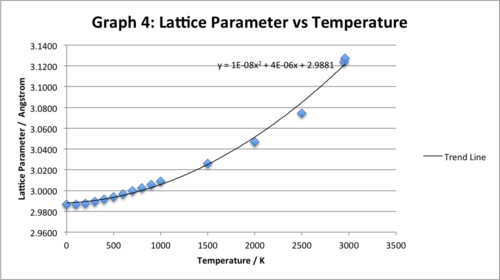
Graph for entire temperature range investigated:

We observe that the higher temperature data points deviate slightly from the trend at the lower temperature data points (the free energy falls at a smaller rate at higher temperature). The resultant new trend line (now trying to represent the correlation between the variables over the entire range) has a slightly different quadratic equation and we see that the data points now do not perfectly fit with new trend line.

Lattice Parameters vs Temperature:

Graph for temperature range: 0K-1000K:

We see that the correlation between the lattice parameter and temperature is also best described with a polynomial relationship. One can observe that all the data points fit carefully with the trend. The lattice parameter increases with increasing temperature - we observe thermal expansion (as expected). This happens as per a quadratic relationship (equation for the trend line is shown on the graph) - i.e. the lattice parameter increases at a faster rate with increasing temperature. At temperatures higher than 2960K, under the quasi-harmonic approximation, the lattice parameter is relatively very large and the system becomes mechanically unstable.

Graph for entire temperature range investigated:

We observe that the higher temperature data points deviate slightly from the trend at the lower temperature data points (the lattice parameter rises at a slightly smaller rate at higher temperatures). The resultant new trend line (now trying to represent the correlation between the variables over the entire range) has a slightly different quadratic equation and we see that now all the data points do not perfectly fit with the new trend line.

Thermal Expansion: Lattice Dynamics (Quasi-Harmonic Approximation) vs Molecular Dynamics

We can use the data collected from the lattice dynamics computations and the molecular dynamics simulations to plot a graph of primitive cell volume vs temperature containing both sets of data. We first plot the graphs for the temperature range 0K - 1000K and then the graph for the entire range investigated. This is to highlight that the data collected for the higher temperatures deviates from the trend in the lower temperature ranges:

Volume vs Temperature:

Graph for temperature range: 0K-1000K:

Graph for entire temperature range investigated:

Overall, we find that the lattice dynamics results indicate the volume of the primitive cell is smaller at all temperatures. There seems to be good agreement with the volumes indicated by the molecular dynamics data in the mid- temperature range of 600K - 1000K. Apart from that, we observe that the volumes indicated by the lattice dynamics data deviates significantly from the volumes indicated by the molecular dynamics data.

At higher T, this is because the lattice dynamics computation ignores higher-order anharmonic effects (e.g. phonon-phonon interactions) which become more important as temperature increases. At lower T, the MD results also indicate lower volumes than the LD computations. This is because the MD simulations do not take into account high-order quantum corrections.

We can use the data from the graphs to calculate thermal expansion coefficients: α_V=(1/V) *(∂V/∂T)

At 300K:

Lattice Dynamics (QHA): V = 18.8901Å₃ Using trend-line equation from Graph 5: ∂V/∂T = 6x10^-7 * T + 0.0002 ∴ α_V (Lattice Dynamics)= 2.0116x10^-5 K^-1

Molecular Dynamics: V = 18.8662Å₃ Using trend-line equation from Graph 5: ∂V/∂T = 1.6x10^-7 * T + 0.0005 ∴ α_V (Molecular Dynamics)= 2.9112x10^-5 K^-1

α_V (Molecular Dynamics) is 45% greater than α_V (Lattice Dynamics). Therefore, there is a significant deviation between the two values at this relatively low temperature.

The experimental value for the thermal expansion (volumetric) coefficient in literature is: 3.12 x 10^-5 K^-1. (at 300K)

This means that α_V (Lattice Dynamics) is 36% lower than the literature value, while α_V (Molecular Dynamics) is only 7% lower than the literature value. This indicates that the molecular dynamics computations provide us with more accurate data at this relatively lower temperature.

We can repeat such calculations to calculate α_V (Lattice Dynamics) and α_V (Molecular Dynamics) at other temperatures. Up till 1000K, we can use the trend-line equation from Graph 5. For higher temperatures, as the data from the quasi-harmonic approximation begins to deviate from the trend, we can use the trend-line equation from Graph 6:

Table 5: Variation of Thermal Expansion Coefficient with Temperature

Again, there seems to be very good agreement between the lattice dynamics data and molecular dynamics data in the mid- temperature range of 600K - 1000K. Apart from that, we observe that the coefficients calculated using the lattice dynamics data deviates significantly from the coefficients calculated using the molecular dynamics data, being much smaller at lower temperatures and much larger at higher temperatures.

Previous investigations have shown that generally the quasi-harmonic approximation is a reasonable approximation in investigating the variation of lattice parameters and volume with temperature, until a temperature of around half the melting point is reached . In this investigation, we have actually found that the lattice dynamics data (volume and thermal expansion coefficient) begins to deviate significantly from the molecular dynamics data above temperatures of 1000K and at very low temperatures (below 300K). At 300K, the lattice dynamics data gives a reasonable approximation of the thermal expansion coefficient.

By studying theory and our data collected, we can understand that the quasi-harmonic approximation is no longer suitable at high temperatures due to interactions between phonons. We realise that the phonon modes represent the actual motions of the ions very poorly as the temperature approaches the melting point. Under the quasi-harmonic approximation, we compute the vibrational frequencies assuming perfectly harmonic vibrations but adjustable lattice parameters at every temperature. While the quasi-harmonic approximation can be used at lower temperatures to account for the anharmonic effect of thermal expansion, intrinsic phonon-phonon interactions are not taken into account in the quasi-harmonic approximation. Within the harmonic approximation (and the quasi-harmonic approximation) - phonons are assumed to be non-interacting. In reality, the phonon interaction is intricate and varies with temperature - the effect becomes prominent at high temperatures.

MD simulations are completely based on classical physics and do not take into account high-order quantum corrections. However, since the simulations use an anharmonic potential curve, MD simulations are able to account for anharmonic effects well. Even in other similar experiments, the MD method is shown to be only very slightly inaccurate at very lower temperatures where quantum effects are larger. In this experiment, we found that at even at a temperature of 300K (ambient T), the Molecular dynamics method gives a very accurate thermal expansion coefficient.

Conclusion

The aim of this investigation was to investigate the phonon dispersion and vibrational density of states of MgO using lattice dynamics, and then using lattice dynamics and molecular dynamics to study the thermal expansion of MgO and compare the results achieved using the two methods.

We were able to study and understand the phonon dispersions curve and density of states curves obtained. We found that increasing the grid-size used gave us more accurate results but was more computationally expensive. By studying the Helmholtz free energy convergence numerically and density of states curves visually, we decided that a grid-size of 16x16x16 gave us a reasonable approximation.

This grid-size was used in our lattice dynamics study of thermal expansion. The data obtained was compared to the data obtained via the molecular dynamics method.

We know that the molecular dynamics method uses classical physics. Therefore, quantum a effects (phonon contributions) are not considered in thermal expansion computations. However, molecular dynamics does use a anharmonic potential. Therefore, molecular dynamics method serves well at higher temperatures where quantum effects are smaller and anharmonicity is more important. In other similar experiments, the MD method is shown to be a very accurate (especially when combined with quantum corrections). In this experiment, we found that even at 300K (ambient T), the Molecular dynamics method gave an accurate thermal expansion coefficient.

We found that for calculations performed at lower temperatures, where anharmonic effects are less important and may be negligible, the lattice dynamics method (using the quasi-harmonic approximation) may also be used to give reasonable results.