Rep:Mod:qwertyuiop3

Module 3, Experiment 3

The Cope Rearrangement Tutorial

Optimizing the Reactants and Products

	HF/3-21G				DFT/6-31G(d)
Optimisation and Conformer	Structure	Summary	Point Group		Structure	Summary	Point Group
Initial Anti, anti1	Pentahelicene		C2		Pentahelicene		C2
Initial gauche, gauche2	Pentahelicene		C2		Pentahelicene		C2
Low-energy gauche, gauche3	Pentahelicene		C1		Pentahelicene		C1
anti2	Pentahelicene		Ci		Pentahelicene		Ci

The initial optimised gauche conformer was, as expected, higher in energy than the intial anti conformer. This is due to the larger amounts of torsional strain in the gauche conformation as the dihedral angle between the carbon groups is smaller.

The energies of the HF/3-21G computed conformers match those in Appendix 1 very well.

There was no difference in the symmetry of the geometries optimisied using HF/3-21G or B3LYP/6-31G(d) methods. However the order of the lowest energy conformation has changed with the anti1 conformation having the lowest energy.

Order of Lowest Energy from Lowest to Highest

HF/3-21G	B3LYP/6-31G(d)
Gauche3	Anti1
Anti1	Anti2
Anti2	Gauche3
Gauche2	Gauche2

In order to explain the change in the ordering, the bond lengths and the dihedral angles of the conformations need to examined.

Bond Lengths Comparisons

Conformer	HF/3-21G Method Bond Length/Å	B3LYP/6-31G(d) Method Bond Length/Å	%Difference
Average anti1 C-C	1.51863	1.52337	0.31
Average gauche2 C-C	1.52490	1.51904	-0.39
Average gauche3 C-C	1.52367	1.51981	-0.25
Average anti2 C-C	1.50687	1.51899	0.80
Average anti1 C=C	1.31611	1.33346	1.30
Average gauche2 C=C	1.31565	1.33308	1.31
Average gauche3 C=C	1.31639	1.33372	1.30
Average anti2 C=C	1.31614	1.33345	1.30

The percentage differences in the C-C and C=C bond lengths for every conformations changed by similar amounts each time therefore the bond lengths would have an insignificant effect on the order of lowest energy conformations.

Dihedral Angle Comparisons

Conformer	HF/3-21G Method Dihedral Angle/°	B3LYP/6-31G(d) Method Dihedral Angle/°	%Difference
Anti1	-176.91	-176.659	-0.14
Gauche2	64.155	65.19	1.59
Gauche3	67.702	66.307	-2.10
Anti2	180	180	0.00

There is a relatively large change in bond angle from a HF/3-21G to B3LYP/6-31G(d) method optimisation resulting in a noticable change in energy for the gauche conformers, when compared to both anti conformers. Therefore the B3LYP/6-31G(d) order of the lowest energy conformations is a result of the anti conformers' geometries remaining largely unchanged whilst the gauche conformers became less stable due to difference in bond angles.

Thermochemistry

	Zero-Point Vibrational Energy/ kcal mol-1	Sum of Electronic and Zero-Point Energies/ HF	Sum of Electronic and Thermal Energies/ HF	Sum of Electronic and Thermal Enthalpies/ HF	Sum of Electronic and Thermal Enthalpies/ HF	Zero-Point Vibrational Energy/ HF	Electronic Energy/ HF
Anti2 HF/3-21G	96.00557	-231.539541	-231.532566	-231.531622	-231.570918	0.15299473	-231.6925357
Anti2 B3LYP/6-31G(d)	89.43574	-234.469196	-234.46186	-234.460915	-234.500721	0.142525032	-234.611721

As the Sum of Electronic and Zero-Point Energies = Electronic Energy + Zero-Point Vibrational Energy, the electronic energy at 0K can be easily calculated using the values of the Sum of Electronic and Zero-Point Energies - Zero-Point Vibrational Energy, which was converted from kcal mol^-1 to HF.

Optimizing the "Chair" and "Boat" Transition Structures

Producing a Guess Chair Transition State

1. Allyl fragment optimised using HF/3-21G level of theory

2. Guess chair transition state structure

1. The first step for producing a guess chair transition state was to optimise an allyl fragment from using HF/3-21G. This optimisation is performed because the shape of the molecules in the chair transition state, without the bonds that formed or broken, are allyl fragments.
2. Now that the allyl fragment has been optimised, a guess chair transition state structure can be produced from two allyl fragments. Two allyl fragments were placed in the same MolGroup of gaussview on top of each other with the terminal groups about 2.2Å apart.

Chair-TS Optimisation: Computing Force Constants on the First-Step

HF/3-21G Level of Theory An optimisation and frequency calculation to a transition state using TS(Berny) was performed on the guess chair transition state structure, with an optimisation keyword of Opt=NoEigen. This keyword prevents the calculation from testing the structure for negative eigenvalues, i.e the calculation does not tests the curvature of the energy potential. The optimisation produced a transition state with a vibrational frequency of -817.979cm^-1.

B3LYP/6-31G(d) Level of Theory Other than the level of theory, the same method was used to optimise the structure to the chair transition state. No problems were encountered.

	HF/3-21G	B3LYP/6-31G(d)
Structure	DOI:10042/to-1119 Pentahelicene	DOI:10042/to-1120 Pentahelicene
Summary
Vibration

Lower and Higher Levels of Theory Comparison

	HF/3-21G	B3LYP/6-31G(d)
Average "Forming/Breaking Bond" Distance/Å	2.02042	1.96756
Average Bond Angle of Allyl Fragment/°	120.510	119.954
Energy/HF	-231.61932242	-234.55698303

Whilst there is not much change in the geometry of the chair transition state, the difference in energy is realtively large with respect to the small difference in the bonding distance and bond angle. Due to the higher and lower theories' geometries being virtually identical, the structure at the minimum of the potential energy surface will be the same for both of these transition states.

It is reasonable to assume that IRC jobs on both transition states would give almost identical structures therefore IRC calculations only need to be run on the lower theory transition state.

IRC

IRC curve with always calculating force constants.

IRC curve with 100 points.

Forward direction, 50 points, calculate force constants once IRC DOI:10042/to-1119 Following the intermediate geometries clearly shows a bond forming on one of the terminal carbon ends indicating a formation of one of the reactants. However after 50 points in a forward direction, it was still not clear as to which conformer the reactant was therefore the minimised geometry still had not been reached. To solve this problem, three solutions were tried:

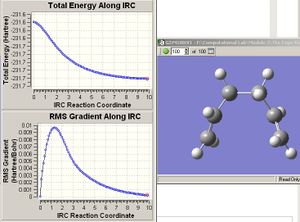
1. Re-running the IRC job in the forward direction with 50 points but always calculating force constants. This approach gave a link 9999 error with the only 14 intermediate geometries. The Total Energy Along IRC curve shows the energy of the geometries increasing with the reaction coordinate.
2. Re-running the IRC job in the forward direction, calculating force constatns once but with 100 points. This approach had no serious problems with the calculation. The final geometry obtained however was still the minimised structure.
3. Running a normal minimum energy optimisation with HF/3-21G(DOI:10042/to-1123 ) and B3LYP/6-31G(d)(DOI:10042/to-1122 )on the initial IRC produced. Optimising using both levels of theory gave gauche2 conformers, each with the correct energy and symmetry for the respective level of calculation. As the B3LYP/6-31G(d) optimisation gave the lowest energy structure straight away, the HF/3-21G calculation will be ignored from now on for further optimisations from IRC jobs.

The only successful solution used to find the minimum conformer of the transition state was the minimum energy optimisation method. Always calculating force constants produced an error which I was unable to resolve. Computing an IRC with 100 points worked without an errors and was closer to the minimum structure than the 50 point calculation therefore if, hypothetically, a minimum energy optimisation gave the incorrect conformer, the optimisation should be re-tried on the final structure of a 100 point IRC job.

Chair-TS Optimisation: Using Redundant Coordinates

Redundant coordinates are a good method of finding a transition state if the initial guess structure was far from ideal.

1. The first step of the method is to freeze the distance between two bond forming/breaking carbons in the guess structure and optimising the rest of the structure to a minimum.
2. Taking this partially optimised strucutre, the same two bonds are then set to Derivative in the redundant coordinate editor and the entire structure is optimised to TS(Berny).

Initially, a distance of 2.2Å was frozen but the subsequent derivative optimisation encountered problems. After looking into the output file, it stated that there were two imaginary frequencies, sugguesting that the geometry used for the derivative calculation was incorrect. It was clear that to solve this issue, two different approaches could be taken:

1. The frozen bond distance needed to be changed - Reducing the bond distance to 2.1Å is expected to solve the issue because the bond distance of a C-C bond is usually smaller than the previously used 2.2Å.
2. Prevent the program from calculating the curvature by using the keyword Opt=NoEigenTest.

Using Redundant Coordinates: Bond Distance to 2.1Å

HF/3-21G Level of Theory

The usual method was used except the frozen bond distance chosen was 2.1Å. The subsequent derivative optimisation went smoothly to give the chair transition state.

Structure	Summary	Vibration
DOI:10042/to-1125 Pentahelicene

B3LYP/6-31G(d) Level of Theory

The B3LYP/6-31G(d) calculation was attempted but after the derivative stage of the ModRedundant was performed, a structure which looked more like a reactant was produced, therefore the result was ignored.

The final structure obtained after ModRedundant derivative calculation: DOI:10042/to-1124

IRC The final geometry of the default setting IRC calculation gave a structure which was similar to the previously mentioned IRC of the computing force constants chair transition state. Therefore the further calculations from before were also carried out on this structure.DOI:10042/to-1126

1. The IRC calculation with always force constants calculated gave a virtually identical structure to the one calculated with the default setting. However, the always force constant structure is lower in energy and the distance between the closer terminal carbons is shorter than in the default setting structure. DOI:10042/to-1127
2. The IRC calculation with 100 points gave an even lower energy structure but this structure still did not resemble any of the reactants therefore it was still not the final structure. DOI:10042/to-1128
3. The optimisation gave the same gauche2 structure as the optimisation method from the previous IRC calculations on the computing force constants chair transition state. DOI:10042/to-1129

	50 Points, Forward, Once force constant calculation	50 Points, Forward, Always force constant calculation	100 Points, Forward, Once force constant calculation	Optimisation after initial IRC
Summary
IRC				-

Using Redundant Coordinates: Using the Additional Keyword "Opt=NoEigenTest"

HF/3-21G and B3LYP/6-31G(d) Levels of Theory

Both calculations went smoothly with no errors encountered. Virtually the same values and the same pattern was observed with the energy, bond distance, bond angles and the negative vibrational frequency between the different level theory structures as the ones from the "force constants in the first-step" chair transition states.

	HF/3-21G	B3LYP/6-31G(d)
Structure	DOI:10042/to-1130 Pentahelicene	DOI:10042/to-1131 Pentahelicene
Summary
Vibration

Lower and Higher Levels of Theory Comparison

	HF/3-21G	B3LYP/6-31G(d)
Average "Forming/Breaking Bond" Distance/Å	2.02071	1.96837
Average Bond Angle of Allyl Fragment/°	120.492	119.951
Energy/HF	-231.61932239	-234.55698295

IRC

The structures given from every IRC calculations, except for when force constants are always calculated, are very similiar to the ones from when the frozen bond was set to 2.1Å. The "always calculate force constants" IRC job experienced the same problem as the one from the "calculate force constants once" chair transition state. As expected, the gauche2 conformer was produced after the optimisation to minimum energy structure.

	50 Points, Forward, Once force constant calculation DOI:10042/to-1134	50 Points, Forward, Always force constant calculation DOI:10042/to-1132	100 Points, Forward, Once force constant calculation DOI:10042/to-1133	Optimisation after initial IRC DOI:10042/to-1129
Summary
IRC				-

Conclusion to Different Optimisation Methods to Chair Transition State

The different chair transition states all have very similar energies and all give gauche2 conformers after IRC calculations. From this, any method can be used to give useful transition states however they should be used at different times:

• Computing force constants on the first-step is the fastest and the best method to use when the guess transition state is close to the actual transition state.
• Using redundant coordinates is slower but a better method to use to when the guess transition state is less similar to the actual because the computation will optimise the guess structure but freezing the forming bonds.

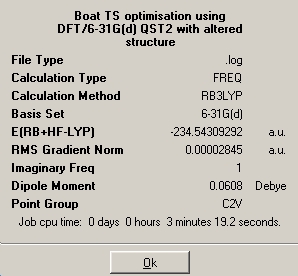
Boat-TS Optimisation: Using QST2

Structure given from errornous QST2 calculation on default anti2 structure

The QST2 is a method where the user specifies the reactant and product of a reaction and the computation finds the transition state of the reaction. The problem of the QST2 method is that the designated reactant and product need to be fairly similar in structure as the transition state. This was demonstrated in the tutorial; when the default anti2 structure was used the an error was given with the problem being associated with program being unable to find the transition state. But when the structures were altered to look more like the transition state, the QST2 calculation finished without any errors.

	HF/3-21G	B3LYP/6-31G(d)
Structure	DOI:10042/to-1137 Pentahelicene	DOI:10042/to-1136 Pentahelicene
Summary
Vibration

Lower and Higher Levels of Theory Comparison

	HF/3-21G	B3LYP/6-31G(d)
Average "Forming/Breaking Bond" Distance/Å	2.14001	2.2071
Average Bond Angle of Allyl Fragment/°	121.697	122.258
Energy/HF	-231.60280218	-234.54309292

As expected, the higher level calculation gave slightly different values for the bond distance and the bond angles. However the opposite is observed to the chair conformations, in which the bond distances and bond angles decrease with increasing level of calculation, whereas with the boat conformations, the values increase.

IRC

From the previous IRC jobs with the chair transition states, I established that the best general method to use to obtain the minimum energy structure was doing a 50 point, forward IRC with force constants calculated once, and then to do a B3LYP/6-31G(d) level minimum energy optimisation.

The structure obtained at the end of jobs was the guache3 conformer.

	50 Points, Forward, Once force constant calculation DOI:10042/to-1139	Optimisation after initial IRC DOI:10042/to-1138
Summary
IRC		-

Activation Energies of Reactions via Transition States

All the activation energies to the transition states are from the anti2 conformer.

	Anti2 HF/3-21G	Anti2 B3LYP/6-31G(d)	Using QST2 Boat TS HF/3-21G	Using QST2 Boat TS B3LYP/6-31G(d)	"Computing Force Constants on the First-Step" Chair TS HF/3-21G	"Computing Force Constants on the First-Step" Chair TS B3LYP/6-31G(d)	Using Redundant Coordinates Bond Distance to 2.1Å HF/3-21G	Using Redundant Coordinates Using the Additional Keyword "Opt=NoEigenTest" HF/3-21G	Using Redundant Coordinates Using the Additional Keyword "Opt=NoEigenTest" B3LYP/6-31G(d)
Sum of Electronic and Zero-Point Energies/HF	-231.539541	-234.469196	-231.450934	-234.402342	-231.466703	-234.414930	-231.466700	-231.466701	-234.414932
Sum of Electronic and Thermal Energies/HF	-231.532566	-234.461860	-231.445307	-234.396008	-231.461343	-234.409009	-231.461340	-231.461341	-234.409010
Sum of Electronic and Zero-Point Energies/kcal mol-1	-145293.1458	-147131.5307	-145237.5441	-147089.5792	-145247.4393	-147097.4783	-145247.4375	-145247.4381	-147097.4796
Sum of Electronic and Thermal Energies/kcal mol-1	-145288.769	-147126.9273	-145234.0132	-147085.6046	-145244.0759	-147093.7628	-145244.074	-145244.0746	-147093.7635
Activation Energy at 0K/kcal mol-1	-	-	55.6017	41.9515	45.7065	34.0524	45.7084	45.7078	34.0511
Activation Energy at 298.15K/kcal mol-1	-	-	54.7558	41.3227	44.6931	33.1645	44.6950	44.6943	33.1639

Experimental Values of Activation Energies at 0K

Chair TS	33.5 ± 0.5 kcal mol-1
Boat TS	44.7 ± 2.0 kcal mol-1

The difference in activation energy between the anti2 and chair transition states from both levels of theory are all very similar further proving that the optimisations to transition state methods are all effective. All of the activation energies match does from appendix 2. The activation energies calculated using HF/3-21G do not match the experimental values but the higher level B3LYP/6-31G(d) calculations match the experimental values very well. From this is can be concluded that the structures obtained from the computations are accurate. The chair TS activation energies are lower than the boat TS values because the atoms in the boat TS are eclipsed, and they are not in the chair TS.

The Diels Alder Cycloaddition

Cis-Butadiene

	Semi-Empirical AM1	B3LYP/6-31G(d)
Structure	Pentahelicene	DOI:10042/to-1141 Pentahelicene
Molecular Orbitals	HOMO - Asymmetric LUMO - Symmetric	HOMO - Asymmetric LUMO - Symmetric

There are no directly noticable differences between the optimisations using either method.

Ethylene and Cis-Butadiene Diels Alder Cycloaddition Transition Structure

The method used to find the transition state was to calcualte force constnts once:

AM1: # opt=(calcfc,ts,noeigen) freq am1 geom=connectivity

B3LYP/6-31G(d): # opt=(calcfc,ts,noeigen) freq rb3lyp/6-31g(d) geom=connectivity

	Semi-Empirical AM1	B3LYP/6-31G(d)	Comments
Structure	Pentahelicene	DOI:10042/to-1140 Pentahelicene	Identical symmetry
Summary			AM1 appears to have an inability to calculate total energies of the structures which it optimises.
Molecular Orbitals	HOMO-1 - Symmetric HOMO - Asymmetric LUMO - Symmetric	HOMO-1 - Asymmetric HOMO - Symmetric LUMO - Symmetric	From molecular orbitals generated from a Semi-Empirical AM1 method and B3LYP/6-31G(d) method gave a different ordering of the HOMO-1, HOMO and LUMO, proves that the AM1 method was not sufficiently good to produce an accurate transition state. In order to produce a bond between cis-butadiene and ethylene, the HOMO and LUMO of either of the two must overlap correctly. The HOMO of cis-butadiene overlaps well with the LUMO of the ethene (DOI:10042/to-1142 ) due to both being asymmetric, therefore it is these two molecular orbitals that interact to form the new σ C-C bonds. By observation, the new molecular orbital that is formed is the HOMO-1 from the B3LYP/6-31G(d) optimisation or the HOMO from the Semi-Empirical AM1. LUMO of ethene - Asymmetric HOMO of cis-butadiene - Asymmetric
Vibration	Vibrational Frequency of -956.084cm-1	Vibrational Frequency of -523.853cm-1	The vibrations corresponding to the bond forming in the reaction path have negative frequency which are synchronous, whereas all of the postive frequencies have no relation to the formation of the product.
Average "Forming Bond" Distance/Å	2.11916	2.272905	Typical sp3 C-C bond length/Å: 1.54 Typical sp2 C-C bond length/Å: 1.33 Van der Waals radius of Carbon/Å: 1.70 The partially formed σ C-C bonds in the transition states of both levels of theory are significantly larger than the typical sp3 and sp2 bond lengths therefore no σ C-C bonds will form if the molecules were to remain in their current location. But the distance of approximately 2.2Å between the bond forming carbons in the transition states is within the combined van der Waals radius of the carbons (1.70Å multiplied by 2 = 3.40Å) therefore there is an interaction present between the atoms, which is suffucient to produce a partial bond.

IRC

IRC jobs were run on the AM1 optimised transition state and then optimised using B3LYP/6-31G(d).

	IRC	Method Used	Product After Optimisation	Total Energy Curve of Product
		# irc=(reverse,maxpoints=50,calcfc) ram1 geom=connectivity	DOI:10042/to-1149 Pentahelicene
Comment	The IRC job optimised the transition state to almost the minimum product, as the gradient was almost zero, however an optimisation was still required.	A reverse direction was used because the forward direction gave the reactants.	From the total energy curve of the product optimisation, it proves that the optimisation was successful.

Cyclohexa-1,3-diene Diels Alder Reaction with Maleic Anhydride

The following transition states for this reaction were optimised using semi-empirical AM1 first then B3LYP/6-31G(d); therefore the transition structures in the following discussion will consist of the optimisations from the higher level B3LYP/6-31G(d) method.

The methods used to find the transition states to the exo and endo structures were QST2 and redundant coordinates respectively.

Exo: # opt=qst2 freq b3lyp/6-31g(d) geom=connectivity

Endo: # opt=(ts,modredundant,noeigen) freq rb3lyp/6-31g(d) geom=connectivity

	Exo	Endo	Comments
Structure	DOI:10042/to-1143 Pentahelicene	DOI:10042/to-1144 Pentahelicene
Summary			As the endo conformation is the kinetic product, the energy of its transition state is expected to be lower, which is proved by comparing the computed energies of the exo and the endo.
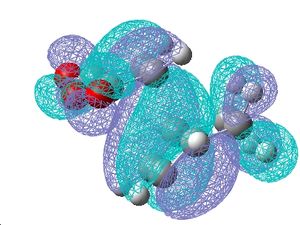Molecular Orbitals	HOMO LUMO	HOMO LUMO	In both conformations, no secondary orbital interaction are observed which is unusual in the endo transition state because the energy was found to be lower. The difference in energy between the conformations must therefore be due to the steric interactions. In the HOMOs of both endo and exo, there are large lobes where the partly formed bonds are suggesting that there is an interaction present which will form the new bond.
Vibrations	Vibrational Frequency of -448.682cm-1	Vibrational Frequency of -446.942cm-1	Both contain one negative vibrational frequency confirming that they are transition states.
Average "Forming Bond" Distance/Å	2.29065	2.268405	There is a very small difference between the distance values of the exo and the endo conformations confirming that there are no secondary orbital interactions present, which is expected to reduce the distance.
Average Through Space Distance/Å	3.028025	2.990165

Mentioned previously in the table above, the difference in energy between the exo and endo conformations should be due to steric repulsions. A reason for the exo transition state being higher in energy and more strained is because the malaic anhydride -C=O-O-C=O- fragment is closer to the hydrogens of the sp³ carbon from the bridge, resulting in unfavoruable steric interactions. The endo transition state does not suffer from the same problem because "opposite" the -C=O-O-C=O- fragment are sp² carbons therefore the hydrogens attached to them are further away than in the exo.

IRC

IRC jobs were run on both exo and endo from the AM1 optimised transition states.

	Exo DOI:10042/to-1146	Endo DOI:10042/to-1145	Comments
Method Used	# irc=(forward,maxpoints=50,calcfc) ram1 geom=connectivity	# irc=(maxpoints=100,calcfc,reverse) am1 geom=connectivity	The IRC was performed at the reverse direction because the forward direction job gave the reactants. This occurs with the diels alder reactions and not the cope rearragement because the potential energy surface for a diels alder reaction is not symemtrical but it is for a cope rearrangement.
IRC			The final structure from both IRC jobs did not give the minimum energy structure.

B3LYP/6-31G(d) optimisations to a minimum was performed on the final IRC structures to give the exo and endo products.

	Exo	Endo	Comments
Stucture	DOI:10042/to-1143 Pentahelicene	DOI:10042/to-1144 Pentahelicene	The two structures came out well after optimisations.
Sum of Electronic and Thermal Energies/HF	Published frequency calculation: DOI:10042/to-1147 -612.559980	Published frequency calculation: DOI:10042/to-1148 -612.562604	The exo product is higher energy for the same reason as the one given for why the exo transition state is higher in energy. The reason was because the malaic anhydride -C=O-O-C=O- fragment is closer to the hydrogens of the sp3 carbon therefore it experiences more steric repulsions. The endo product's malaic anhydride -C=O-O-C=O- fragment is "opposite" sp2 carbons, which does not have hydrogen facing towards the anhydride fragment.
Sum of Electronic and Thermal Energies/kcal mol-1	-384386.9	-384388.5

Conclusion of Module

The three methods used to produce the transition states were all successful. However, the method of calculating force constants once at the beginning of a calculation is relatively unreliable for more complex diels alder cycloadditions. This is shown by the fact that the previously mentioned method was used for the simple cis-butadiene and ethylene reaction whilst QST2 and redundant coodinates were used for the cycloaddition reaction between cyclohexa-1,3-diene and maleic anhydride. The IRC jobs from the transition states were also successful at producing the minimum energy structures; and gave energy values which were capable of producing conclusions when comparing between the exo and endo structures.

Whilst the methods used did indeed produce transition states, they are not as accurate as they could be. This is because correlation effects are neglected in the methods used. A method which does take these effects into account is MP2.