Rep:Mod:qwertyuiop1

Module 1: Structure and spectroscopy (Molecular mechanics and molecular orbital)

The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

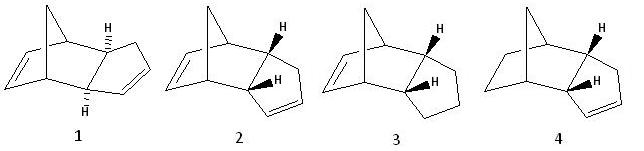
The Hydrogenation of Cyclopentadiene Dimer

Hydrogenation of compound 2, cyclopentadience dimer, gives either compound 3 or 4.

Energies of Compounds

Compound number	Stretch, kcals mol-1	Bend, kcals mol-1	Stretch-Bend, kcals mol-1	Torsion, kcals mol-1	Non-1,4 VDW, kcals mol-1	1,4 VDW, kcals mol-1	Dipole/Dipole, kcals mol-1	Total Energy, kcals mol-1
1 Pentahelicene	1.2923	20.5870	-0.8413	7.6715	-1.4358	4.2320	0.3778	31.8834
2 Pentahelicene	1.2454	20.8603	-0.8320	9.5039	-1.5083	4.3012	0.4448	34.0153
3 Pentahelicene	1.2324	18.8641	-0.7625	12.2469	-1.5627	5.7523	0.1631	35.9337
4 Pentahelicene	1.0963	14.5074	-0.5394	12.4972	-1.0507	4.5124	0.1407	31.1540

When comparing the different energy contributions to the total energy each of stereoisomer, a noticeable difference is observed only in the torsion energy. The torsion energy of the exo dimer is smaller due to less torsional strain as the stereoisomer is closer to a staggered conformation, as shown in the table below.

Secondary orbital interactions are shown with a green dashed line, whereas the red lines show the bonds which are forming.

Compound number	1	2
Dihedral Angle/°	178.9829	-46.7943
Image

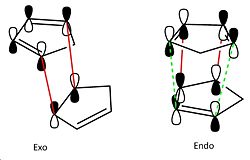
The exo dimer has a lower total energy so is expected to form because it is the thermodynamically stable product. However, in the dimerisation of cyclopentadiene, the endo dimer is mainly formed because the mode of dimerisation is via kinetic stabilisation. This is due to the stabilising HOMO and LUMO interactions called secondary orbital interactions between each conjugate system which can only occur in the transition state of the endo-product formation hence it is the major product.

Relative to compound 2, the total energy of compound 3 is higher whilst the total energy of compound 4 is lower. As compound 4 is more thermodynamically stable than the reactant, it will form when compound 2 is hydrogenated. Comparing the different energy contributions of compound 2 and 3, the decrease in bend energy does not compensate for the increase in torsion and 1,4 Van der Waals energy; whilst for compound 4, the larger decrease in bend energy does compensate for the increase in torsion and 1,4 Van der Waals energy. The decrease in bend energies are due to a loss of a C=C double bond allowing the rings to become more flexible. Compound 4 has a greater decrease because the loss of its C=C double bond gives greater flexibility to two rings, whilst in compound 3 only one ring is made more flexible.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Compound number	Dihedral angle with respect to the aromatic ring/°	Total energy, kcals mol-1
1 Pentahelicene	48.6861	24.9512
2 Pentahelicene	-41.6123	14.8540

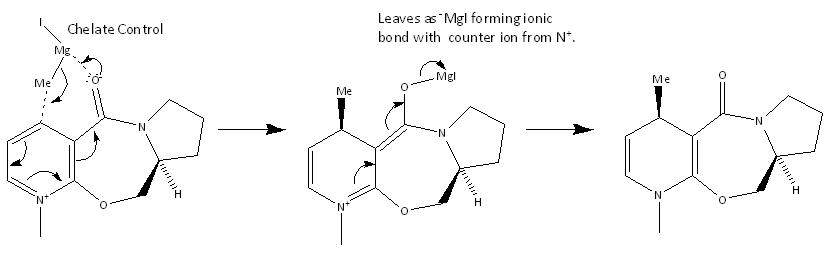
Mechanism of compound 5 to 6

The diastereofacial selectivity of the addition of a methyl group via a Grignard reaction is due to chelate control. The dihedral angle of the carbonyl with respect to the aromatic ring is 48.6861° suggesting it is facing towards a specific side of the ring. As the magnesium atom is electron-deficient, it chelates to the electron-rich carbonyl oxygen during the reaction forcing attack to occur on the side of the ring where as the carbonyl is pointing towards.

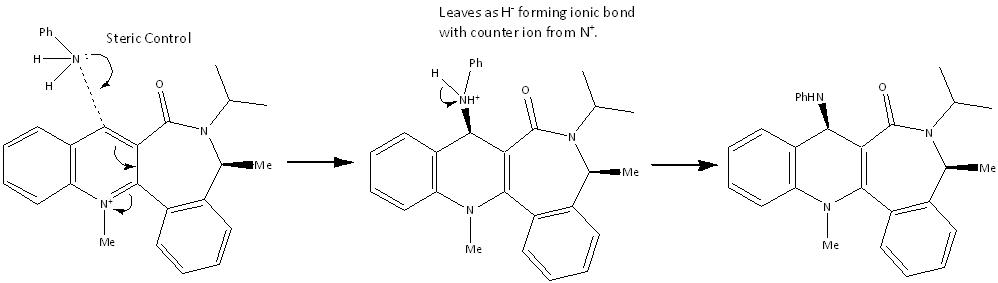
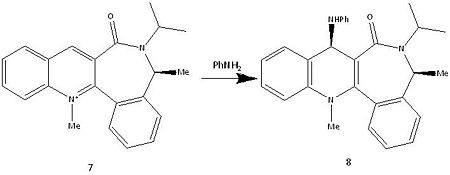
Mechanism of compound 7 to 8

The absolute stereochemistry of the compound 8 from the reaction shown below is due to steric control caused by the carbonyl. The amine attacks the opposite side of the ring that the carbonyl is facing towards (into the page).

When a MM2 energy optimisation was run with compound 5 and the grignard reagent simultaneously, ChemBio3D Ultra gave an error message saying, “WARNING! No atom type was assigned to the selected atom!” This is because metal atoms (eg. Magnesium) and ions have not been experimented on largely and implemented into molecular mechanics; and MM2 is parametric method relying on interpolating data gained from experiments and known molecules. Thus molecular mechanics cannot be used on compounds containing unusual or uncommon groups as it would return inaccurate results. MM2 also does not account for transition state structures therefore cannot be used to model the kinetics of a reaction, as it does not account for orbital interactions and electronic effects such as aromaticity well.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Compound number	Stretch, kcals mol-1	Bend, kcals mol-1	Stretch-Bend, kcals mol-1	Torsion, kcals mol-1	Non-1,4 VDW, kcals mol-1	1,4 VDW, kcals mol-1	Dipole/Dipole, kcals mol-1	Total Energy, kcals mol-1
Up Pentahelicene	2.6952	15.7999	0.3934	18.1874	-0.9492	12.6138	0.1489	48.8894
Down Pentahelicene	2.5000	12.8192	0.2876	17.7030	-0.7591	12.1468	0.2608	44.9583

The differing stabilities of the two atropisomers are mainly due to the dihedral angle of the neighbouring hydrogen with the carbonyl group, i.e. the more eclipsed the neighbouring hydrogen is to the carbonyl the higher the energy and the less stable the atropisomer.

Atropisomer	Dihedral angle across C=O/°	Image
Carbonyl pointing up	20.6999
Carbonyl pointing down	-51.0006

The atropisomer with the carbonyl pointing up has the smaller angle therefore experiences more torsional strain and is less stable, which backs up the higher energy calculated by the MM2 optimisation.

Another less serious reason of how the stability of the atropisomers can be affected is in the dihedral angle between the C=C double bond and the bridging group next to it.

Atropisomer	Carbonyl pointing Up	Carbonyl pointing Down
Dihedral Angle across C=C bond/°	10.7561	-1.4882
Image

Alkene reactivity

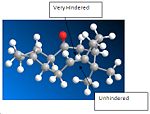
The C=C double bond and the bridging group next to it, in both atropisomers, are not planar with respect to a normal alkene. However, as the atropisomer with the carbonyl pointing down has a smaller dihedral angle, it is expected to have a lower total energy than the atropisomer with the carbonyl pointing up; which is demonstrated by the MM2 energy optimisation displayed above in the table.

The C=C double bond on both atropisomers reacts slower than a normal alkene because the the C=C double bond is very hindered by the bridging carbons and the ring, resulting in only one side of the alkene being is avaliable for electrophilic attack; whilst a normal alkene would not have as much protection hence is more reactive.

How one might induce room temperature hydrolysis of a peptide

Conformation	Stretch, kcals mol-1	Bend, kcals mol-1	Stretch-Bend, kcals mol-1	Torsion, kcals mol-1	Non-1,4 VDW, kcals mol-1	1,4 VDW, kcals mol-1	Dipole/Dipole, kcals mol-1	Total Energy, kcals mol-1
Equatorial OH/Axial Ethylamido Pentahelicene	1.4387	7.8239	0.5977	11.7073	-8.1988	10.4714	-4.5520	19.2883
Equatorial OH/Equatorial Ethylamido Pentahelicene	1.6615	5.4489	0.5764	8.4513	-5.9377	9.5149	-6.2642	13.4510
Axial OH/Axial Ethylamido Pentahelicene	1.5200	5.0660	0.5466	9.0063	-7.1165	9.6173	-6.5801	12.0596
Axial OH/Equatorial Ethylamido Pentahelicene	1.5610	3.2789	0.4890	7.1684	-8.0841	9.7706	-5.1528	9.0309

For both isomers, the most stable conformations are when the ethylamido group is equatorial because if it was axial then there would be large amounts of 1, 3 diaxial compression with the axial hydrogens.

1, 3 diaxial compressions in the isomers

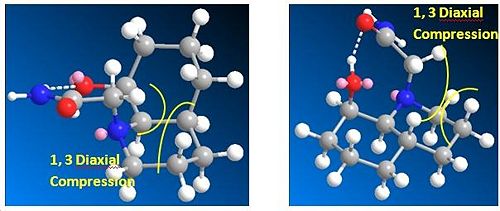
Other than reducing 1, 3 diaxial compressions, hydrogen bonding between the nitrogen or oxygen in the ethylamido group and the hydroxyl hydrogen also occurs in the all of the structures to reduce the total energies.

For hydrolysis to occur in either isomer, both the ethylamido group and hydroxyl group must be either axial or equatorial. The most stable conformation of the isomer which has the axial hydroxyl group is when the ethylamido is equatorial therefore hydrolysis cannot occur as the angle of approach required is incorrect. For a reaction to occur on this isomer, it must change into the higher energy one with the ethylamido group in the axial position, requiring 3.0287kcal mol^-1 of energy hence hydrolysis occurs very slowly. The most stable conformation of the isomer with an equatorial hydroxyl group is when the ethylamido group is also equatorial therefore no conversion of the conformation is needed to initiate hydrolysis therefore the rate of reaction is high.

Hydrogen bonding also locks the ethylamido and hydroxyl groups into specific locations restricting their rotation therefore preventing the lone pairs of the hydroxyl oxygen interacting with the π* orbital of the carbonyl. The required angle of attack on the carbonyl is called the Bürgi-Dunitz angle and is 107° between the C=O and the attacking O. Only in the conformer with the hydroxyl and ethylamido group in equatorial positions, a hydroxyl oxygen lone pair is directed towards the π* orbital of the carbonyl assisting the hydrolysis.

Conformation	Equatorial OH/Axial Ethylamido	Equatorial OH/Equatorial Ethylamido	Axial OH/Axial Ethylamido	Axial OH/Equatorial Ethylamido
Image (Dashed, white line represents H-bond)
Comment	Incorrect orbital orientation for overlap and the carbonyl and hydroxyl groups are too far apart.	Attacking lone pair in line with π* and pointing in correct direction.	Incorrect orbital orientation for overlap with lone pairs pointing away from the carbonyl.	Incorrect orbital orientation for overlap with lone pairs pointing away from the carbonyl.

The conformation with an equatorial OH and equatorial ethylamido is most likely to hydrolyse because it is the most likely to attack the carbonyl from 107° as it does not need to move far or distort much in order to acheive this angle.

On the left has the branching out group. It clearly shows that it is more unlikely than the normal conformer to hydrolyse

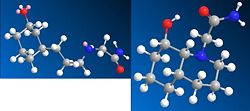
The hydrolysis occurs much faster in these compounds because the ethylamido group and the reacting hydroxyl group is on the same molecule thus the order of reaction is one. The hydrolysis of a peptide bond between two reactants at neutral pH and 25°C is expected to usually take 500 years because the reacting groups are on two different molecules therefore the order of reaction is two. As two different molecules need to react, the probability of a reaction occuring is very low compared to the isomers. Enzymes are able to catalyse the reaction because it aligns the conformations so that the two reacting groups are in the ideal locations for hydroysis to occur.

Modelling Using Semi-Empirical Molecular Orbital Theory

Non-hydrogenated compound 12 PM3 Optimised

Pentahelicene

Non-hydrogenated compound 12 DFT Optimised

Pentahelicene

Monohydrogenated compound 12 DFT Optimised

Pentahelicene

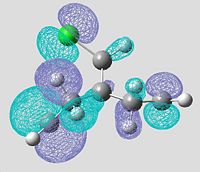
Molecular Orbitals of Non-hydrogenated Compound using PM3 Energy Optimisation

HOMO-1 (MO31)	HOMO (MO32)	LUMO (MO33)	LUMO+1 (MO34)	LUMO+2 (MO35)

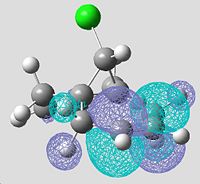
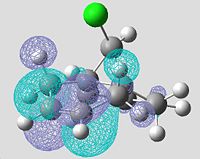
An error was given after the DFT optimisation of the monohydrogenated compound even after 50 optimised geometries. The error said: "Error termination request processed by link 9999. Error termination via Lnk1e in /apps/gaussian/g03_e01/g03/l9999.exe at Sun Oct 19 20:18:43 2008", which means I have insufficient of optimisation cycles. Looking at the intermediate geometries, at about intermediate 25, the geometry of the molecule did not change much by the time it reached intermediate 50 therefore I just used this incomplete DFT optimisation structure for my frequency calculation.

Molecular orbital diagram showing which orbitals interact

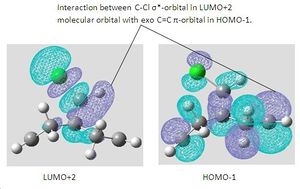
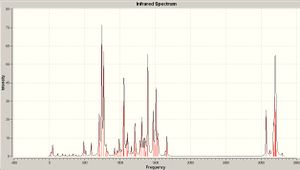
Stretching frequencies of the C=C bond and C-Cl

Compound	Exo C=C Stretching Frequency/cm-1	Endo C=C Stretching Frequency/cm-1	C-Cl Stretching Frequency/cm-1
Non-Hydrogenated	1760.95cm-1, 3.9086 Intensity	1740.77cm-1, 4.1417 Intensity	772.633cm-1, 25.2144 Intensity
Hydrogenated	-	1761.7cm-1, 4.3221 Intensity	776.879cm-1, 20.172 Intensity

Published IR for the non-hydrogenated compound: DOI:10042/to-1010 Published IR for the hydrogenated compound: DOI:10042/to-1011

As the endo C=C bond orbitals are not involved in strong orbital interactions, the frequencies of the stretches are not large.

IR frequency equation

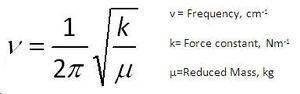
The interaction between the C-Cl σ*-orbital in the LUMO+2 and the exo C=C π-orbital in the HOMO-1 involves a transfer of electron density from the exo C=C π-orbital to the anti-bonding C-Cl orbital therefore weakening the C-Cl bond. The frequency of a band in infrared spectroscopy is given by the equation on the right of the page. the Force constant is essentially a measure of the bond strength therefore the C-Cl bond k value would decrease from its normal value after the interaction with the exo C=C π-orbital. As the frequency is proportional to the force constant, the frequency of the C-Cl IR stretch will decrease. A prediction that can be made is that when the exo C=C π-orbital is hydrogenated, an increase in the frequency of the C-Cl stretching frequency will be observed as the force constant would be greater because there would no longer a π-orbital to interact with.

The C-Cl stretching frequency in the non-hydrogenated compound was calculated to equal 772.633cm-1 whilst the frequency in the hydrogenated compound was 776.879cm-1, confirming the prediction that an increase in the frequency would be observed.

Non-hydrogenated compound distances, DFT optimised (left) and PM3 optimised (right)

Non-hydrogenated compound distances

	Distances/Å
DFT optimised Exo carbons to bridgehead carbon	3.0295
DFT optimised Endo carbons to bridgehead carbon	3.2844
PM3 optimised Exo carbons to bridgehead carbon	3.0414
PM3 optimised Endo carbons to bridgehead carbon	3.4514

Hydrogenated compound distances

Hydrogenated compound distances

	Distances/Å	Average Distances/Å
Exo carbons to bridgehead carbon	3.0708 3.3605	3.2157
Endo carbons to bridgehead carbon	3.2613 3.2635	3.2624

As there was an interaction between the C-Cl σ*-orbital and the exo C=C π-orbital in the non-hydrogenated compound, the distance between the exo carbon double bond and the bridgehead carbon is shorter than the endo carbon double bond to the same bridgehead carbon by 0.41Å for the PM3 optimised non-hydrogenated compound which matches literature values. The same two distances in the monohydrogenated compound are similar in distance, as expected, due to no orbital interaction between the C-Cl σ*-orbital and the exo C=C π-orbital.

Assigning Regioisomer in "Click Chemistry"

Mechanism to form isomer A using a Ruthenium(II) catalyst

The first step of the mechanism to form isomer A is oxidation addition via nucleophilic attack by the azide then the addition of an alkyne which becomes internally bound to the ruthenium catalyst. Several steps follow (as given in the mechanism) then the product A is removed from ruthenium via reductive elimination.

Mechanism to form isomer B using a Copper(I) catalyst

The first step of the mechanism to form isomer B is the removal of the acidic proton from the alkyne using a base then the copper (I) catalyst is oxidatively added terminally to the alkyne. A 1,3 dipolar cycloaddition and reductive elimination follow to give the product B.

Ruthenium(II) catalysts give only the 1,5 isomer because the alkyne cannot terminally bind to it whereas in copper(I) catalysts the alkyne can only bind terminally hence different isomers are observed when using different catalysts.

The key spectroscopic technique which can be used to differentiate between the two isomers is from ¹³C NMR. Another method of determining which isomer is present is to observe the chemical shift for the hydrogen labelled with “19”. The chemical shift of this proton will be more deshielded in the 1,4 isomer as the aromatic system in this isomer is larger as hence has a stronger effect on chemical shift. Unfortunantly the DFT NMR calculations are not particularly reliable for proton NMR chemical shift therefore the computations could not be used to back up this theory. IR and optical rotations are not particularly useful for differentiating between the isomers because they both contain the same functional groups so the IR spectra will contain similar peaks (but at different intensities) as they both have C1 point groups and both isomers have no chiral centres.

Isomer A IR Spectrum

Isomer B IR Spectrum

¹³C NMR Chemical Shifts for Isomers A and B

Compound A jmol

Isomar A with labelled atoms

Pentahelicene

Compound B jmol

Isomar B with labelled atoms

Pentahelicene

Chemical Shifts on isomer A, ppm δ	57.9446 (6)	120.68 (5)	124.735 (18), 125.286 (14)	127.594 (12), 127.778 (16), 127.815 (7), 128.238 (9), 128.312 (10)	128.44 (17)	128.643 (15)	128.937 (11)	130.831 (13)	136.386 (8)	148.434 (1)
Literature, ppm δ	54.0	119.5	125.5	127.9	128.56	128.64	128.9	130.4	134.6	148.0
Chemical Shift on isomer B, ppm δ	55.8523 (6)	127.512 (9)	127.889 (10)	128.185 (18), 128.251 (12), 128.363 (7), 128.487 (11), 128.605 (13)	128.726 (17)	128.89 (15)	129.361 (16)	130.076 (14)	133.614 (1)	134.999 (8)	139.946 (5)
Literature, ppm δ	51.85	126.93	127.22	128.22	128.92	129.08	129.64	133.26	133.34	135.66	138.26

Published NMR for the 1,4 isomer: DOI:10042/to-991 Published NMR for the 1,5 isomer: DOI:10042/to-988

Computed ¹³C chemical shifts for both isomers match the literature data well with no need to correct for spin-orbit coupling errors. The only chemical shifts which have more noticeable differences are 57.9446δ and 55.8523δ. The carbon which these two chemical shifts correspond to is the methylene carbon; and as the same carbon was the problem both times, the difference in chemical shift is likely due the calculation done rather than the optimisation of the isomer since the other chemical shifts are accurate.

The 1,4 isomer gave a chemical shift of 148.434δ which corresponds the carbon labelled with “1”. The same carbon on the 1,5 isomer had a chemical shift of 133.614δ.The chemical shift of carbon “1” in the 1,4 isomer is much larger than the carbon “5” because the aromatic system from the phenyl ring and the 1,2,3 triazole (which are both in the same plane) attached to it is deshielding the carbon. The rings in the 1,5 isomer are not in the same plane as each other therefore no aromaticity is observed between them, hence less the deshielding occurs. As the highest chemical shift values are very different, the best method of differentiating between the two isomers is to identify whether the highest chemical shift peak is above closer to the value for either of the isomers.