Rep:Mod:qpzm1029

Module 1: Structure and spectroscopy (Molecular mechanics and molecular orbital)

Introduction

This experiment aims to utilise molecular modelling and computational calculations in order to predict characteristics of chemical reactions such as stereoselectivity. The first series of exercises will mainly use molecular mechanics calculations (MM2), which attempt to move the atoms in a molecule so that it minimises the overall energy. It assumes that the total energy consists of:

1) Bond stretches between two atoms - how far the bonds are from their prefered lengths

2) Bending of bonds between three atoms - how far the angles between atoms around a centre are from their prefered angles

3) Torsional strain between four atoms - how far the torsion angles for atoms 3 bonds apart are from their prefered angles

4) Van der Waals repulsions - the repuslion between the electron clouds of the atoms in the molecule

5) Dipole-dipole (or H-bonding) electrostatic interactions - stabilising electrostatic interactions between atoms in different parts of the molecule

MM2 breaks down the total energy into the above components, which is useful to see where the majority of the destabilisation (or stabilisation) arises from. This method is good for determining energies of the products, but is unable to analyse a transition state structure so the energies obtained for different isomers only give us information about the relative thermodynamic stabilities.

Where information about the transition state would have been useful, the molecular (orbital) surfaces can be calculated and represented graphically. The presence of any electronic interactions between orbitals which would favour one particular orientation or approach of a molcule can then be predicted. This will be demonstrated as early as the first exercise.

The Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

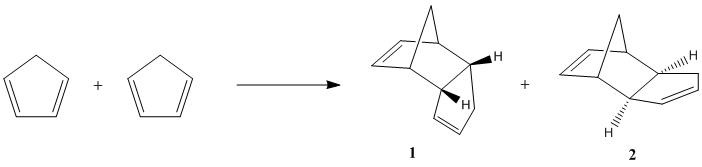
The dimerisation of cyclopentadiene is a [4+2] cycloaddition process which has two possible modes of dimerisation, giving either exo product 1 or endo product 2. Molecular mechanics can be used to determine which of products 1 and 2 is the more thermodynamically stable isomer. The optimised structures and energies obtained from the MM2 calculation were found as the following:

Exo product 1

Endo product 2

Energy component (kcal/mol)	Exo product 1	Endo product 2
Stretch	1.2923	1.2515
Bend	20.5870	20.8585
Stretch-bend	-0.8413	-0.8393
Torsion	7.6715	9.5146
Non-1,4 VDW	-1.4358	-1.5614
1,4 VDW	4.2320	4.3327
Dipole-dipole	0.3778	0.4497
TOTAL	31.8834	34.0063

We can see from the total energies that according to MM2, the exo isomer is more thermodynamically stable than the endo isomer by 2.1229 kcal/mol. Looking at the different compononents of overall energies for products 1 and 2, the difference of 2.1229 kcal/mol is mainly accounted for by an increase in the torsional strain by 1.8431 kcal/mol. The origin of this increase in energy can be seen by looking at the torsion angles of the four carbons (on both sides of the molecule) which have been marked below by a black line.

Exo product 1

Endo product 2

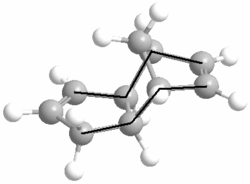
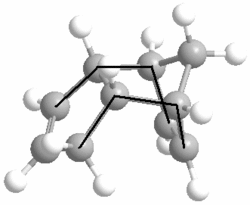
Product 1 has the marked carbons at 177.5^O and 179.0^O, while for product 2 they are at 46.8^O and 50.4^O. The exo product has the large, carbon groups much closer to the preferred 180^O (anti-periplanar) torsional angle, whereas the endo product has them at a much lower, disfavoured angle and is thus significantly less stable than its exo isomer.

However, we know form the so-called 'endo rule' of Diels-Alder cycloadditions that unless there are other factors involved, the product will form with endo isomerism so the endo isomer, product 2, is the expected major product. This is not represented by the energies predicted by the MM2 calculations, therefore the reaction must be under kinetic control. What this means is that the isomer is predominantly determined by the stability of the transition state rather than the stability of the product.

Unfortunately MM2 can't model the transition state so in order to get an idea of what happens in the transition state, the molecular orbitals for cyclopentadiene have been calculated. This was done using a Gaussian calculation, using method and basis set HF/STO-3G.

The approach taken by the cyclopentadiene molecules to form an exo dimer and the dotted lines show the new bond that is being formed. The molecular orbitals show the overlap between the HOMO and the LUMO, with the HOMO approaching the LUMO from the top.

The approach taken by the cyclopentadiene molecules to form an endo dimer and the dotted lines show the new bond that is being formed. The molecular orbitals show the overlap between the HOMO and the LUMO, with the HOMO approaching the LUMO from the top.

It can be seen in the above image that despite the fact that the same number of bonds are being formed in both the exo and endo cases, the molecular orbitals overlap to a greater degree during the endo approach. In order to see this overlap more clearly, we can redraw the molecular surface in terms of the atomic orbitals in the HOMO and the LUMO and this is shown below.

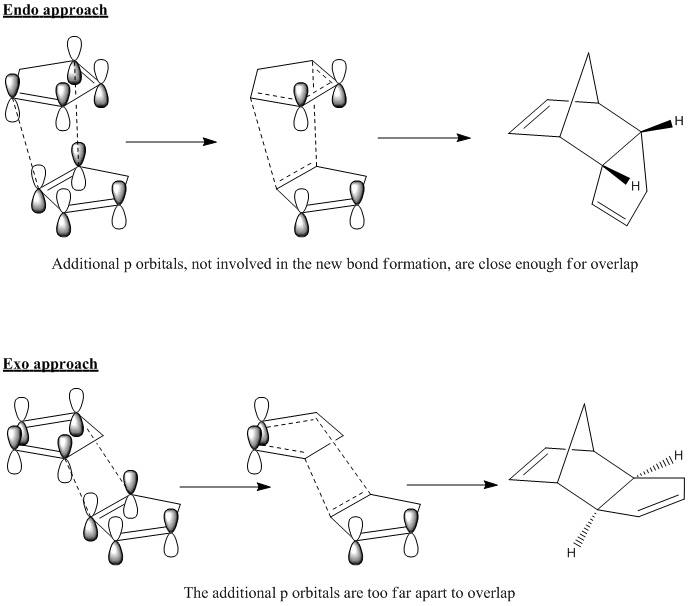
The drawn atomic orbitals clearly illustrate the additional through-space bonding interactions experienced by cyclopentadiene molcules in an endo dimerisation orientation, which stabilise this transition state. There is no such bonding overlap in an exo approach because the additional p orbitals are too far apart in this orientation. Therfore it can be seen that the endo product is favoured kinetically and will be formed faster, making it the major product. By combining MM2 and molecular orbital calculations, we have effectively explained the origins of the endo rule.

Predicting the Site of Hydrogenation

Another characteristic of cyclopentadiene dimer which can be investigated with techniques we have already used is the rate of hydrogenation at each of the double bonds. The simple reaction scheme is given below:

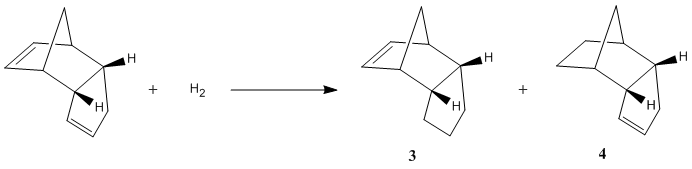
First of all, we can look individually at each of the two double bonds in the molecule and see how they differ. It was found that bond lengths of each alkene are consistent with the prefered C=C bond length of 1.54 angstroms, however, the bonding angles differ. The bond angles to be analysed are marked below.

The C=C bond which would lead to product 3 when hydrogenated

The C=C bond which would lead to product 4 when hydrogenated

The angles for the C=C bond which hydrogenates to product 3 are 113.0^O and 112.7^O, while for the product 4 C=C bond they are 107.5^O and 107.6^O. None of these the prefered 120^O for an sp² centre. However, they are much closer for the product 3 C=C, meaning this alkene bond is more stable. The product 4 C=C is more strained and is in fact very close to the prefered 109.5^O bond angle for an sp³ centre. From this, we can logically predict that this alkene bond will more readily undergo hydrogenation to relieve some of its angle strain.

Now, using molecular mechanics, we can ascertain a thermodynamic prediction of which of 3 and 4 will be the thermodynamically more stable product. The energies found using MM2 for hydrogenated products 3 and 4 are as follows:

Energy component (kcal/mol)	Product 3	Product 4
Stretch	1.2324	1.0963
Bend	18.8641	14.5074
Stretch-bend	-0.7625	-0.5493
Torsion	12.2469	12.4972
Non-1,4 VDW	-1.5627	-1.0507
1,4 VDW	5.7523	4.5124
Dipole-dipole	0.1631	0.1407
TOTAL	35.9337	31.1540

The most stable hydrogenated product is product 4 by 4.7797 kcal/mol, so it is therefore the thermodynamic product. Breaking down this energy somewhat, we can see there are small, noticeable differences in the stretching and van der waals energies but these mostly cancel each other out. As the difference in bending strain of 4.3567 kcal/mol is very similar to the overall energy difference between the products, we can presume that this is the most significant factor for the preference of 4 over 3.

As already stated, product 4 has less bending strain than product 3 by 4.3567 kcal/mol and this is most likely due to the fact that in this product, the hydrogenation of the double bond gives the carbons on the bridged ring greater flexibility so they can take more favourable angles. This in effect counteracts the restrictive nature of the bridge which already pushes some of the C-C-C bonds away from their prefered angles.

On the other hand, the planarity and hence limited flexibility of the π bond on the bridged ring forces some of the bond angles to more energetically demanding values. It would have been interesting to quantify some of the angles in the bridged ring for products 3 and 4 for comparison, but due to time constraints for this experiment it would be more time efficient to move on.

However, we have made a reasonable thermodynamic prediction that 4 is indeed the major product due to its lower overall energy compared to 3 and also due to the greater relief of bond angle strain upon hydrogenating the double bond in the dimer which leads to 4.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue)

An Optically Active Derivative of Prolinol

In the first part of this exercise, the following reaction will be studied:

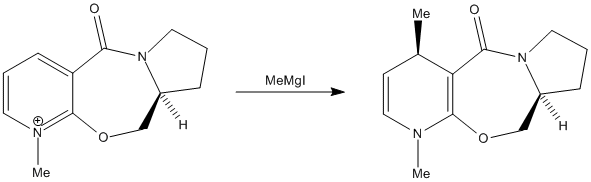
Nucleophilic addition of a methyl group to the pyridinium ring yields a product with the absolute stereochemistry shown above. In order to rationalise this stereochemistry, the structure of the prolinol starting material will be modelled using MM2 molecular mechanics. The lowest energy conformation was found to be the following:

Energy component (kcal/mol)	Prolinol derivative
Stretch	0.8829
Bend	6.5320
Stretch-bend	0.1153
Torsion	9.5698
Non-1,4 VDW	-2.6693
1,4 VDW	11.5144
Charge-dipole	3.3654
Dipole-dipole	-3.7742
TOTAL	25.5363 kcal/mol

Noticeable from the above table, is a new compononent of the overall energy, which is termed as "charge-dipole". This is most likely due to the relative instability of having a charged species. Although we have obtained an overall energy, it doesn't really help explain the reason for the stereochemistry observed by Grignard addition. In order to get more insight into the mechanism of addition which gives the stereochemistry shown, we will investigate the orientation of the carbonyl group which is 1,3 to site of attack. This is more clearly seen by the 3D, rotatable structre so this is shown below.

NAD first qpzm1029

It can be observed from the structure, that relative to the planar, pyridinium component of the molecule, the carbonyl oxygen points up. In ChemBio3D, it was found the the dihedral angle is 42.3^O which is fairly significantly up-facing. With this knowledge, coupled with the fact the that methyl group always adds with up-facing stereochemistry, we can suggest the following mechanism for the reaction:

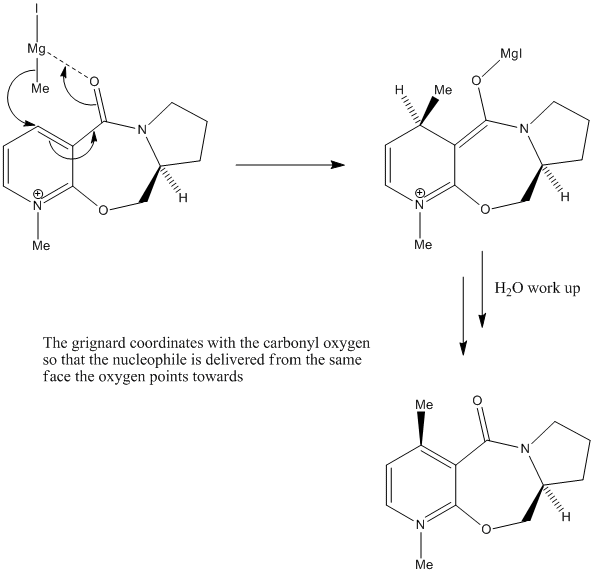
The mechanism is based on the electron defficiency of the magnesium atom in the Grignard reagent. In order to remove some of this defficiency, the magnesium coordinates to the oxygen by accepting one of its lone pairs which locks the Grignard in a position above the plane of the pyridinium ring, thus delivering the methyl group exclusively from the top face.

It would have been interesting to model the coordinated Grignard reagent before addition of the methyl group in order to confirm this would indeed put the methyl in a reactive orientation to the 4 position of the pyridinium ring, but ChemBio3D gave an error when attempting to do this, presumabely because it is only programed to deal with common organic atoms so did not recongise the magnesium atom.

Another point to consider, is that the (methyl) nucleophile is relatively small, so sterics do not play so much of a major role here i.e. they do not counteract the co-ordinating power of the magnesium. Had the nucleophile been larger, such as a phenyl group for example, not only would we have had to worry about the down-facing stereoisomer, but also the regioisomer of addition to the 6 position, although this is somewhat hindered by the methyl group on the 1 position.

Stereochemistry of an Alternate Prolinol Derivative

A different derivative of prolinol will now be investigated to see what difference can be achieved by changing the nucleophile as well as some of the functionality in the molecule. The new reaction scheme is as follows:

The lowest energy conformation was found to be the following:

Energy component (kcal/mol)	Prolinol derivative
Stretch	1.5273
Bend	6.6861
Stretch-bend	0.3394
Torsion	-6.0170
Non-1,4 VDW	-2.5891
1,4 VDW	17.6942
Charge-dipole	2.3297
Dipole-dipole	-4.8198
TOTAL	15.1508 kcal/mol

And the 3D structure:

NAD second qpzm1029

As the orientation of the carbonyl group was the determining factor in the stereochemistry of the previous example, the big difference in this case is that the carbonyl is now pointing downards. By looking at the other parts of the molecule we can see the reason for this.

In the previous example, the substituent on the nitrogen in the 7 membered ring was part of a fused cyclopentane, which due to its own restrictive ring-like nature, was forced to point outwards (5.9^O dihedral angle). In this example, the nitrogen has an isopropyl substituent, which has greater flexibility and points significantly more upwards (67.0^O dihedral angle) due to its branching. Consequently, the methyl group coming off the carbon adjacent to the nitrogen prefers to go axial to avoid steric clash with the isopropyl. This in turn, forces the carbonyl oxygen to face downards at a dihedral angle of -42.1^O.

Now, if we consider the nucleophile, it differs from the Grignard reagent in that it has no electron defficiency so does not possess the ability to coordinate with the carbonyl oxygen. It in fact has a lone pair on the nitrogen atom, which it uses to attack the pyridinium ring directly. From this, we can suggest the following mechanism:

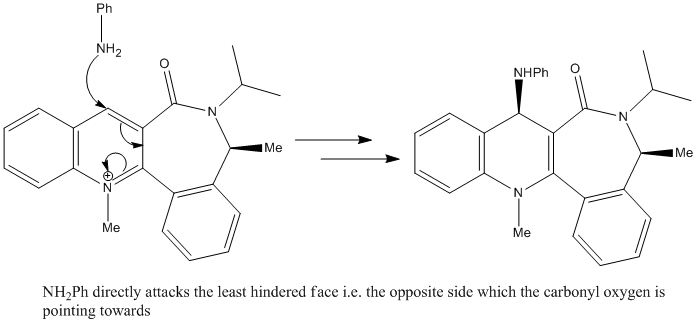
As the mechanism involves direct attack to the pyridinium ring, the main determining factor for the stereochemistry is now sterics, so the nucleophile appraoches the molecule from the face opposite to that of the down-facing carbonyl oxygen. This, as shown in the reaction scheme, results in up-facing stereochemistry of the added amine group.

Another thing to note, is that this nucleophile contains a phenyl group so is much larger than the (methyl) Grignard reagent. This increases the effect of steric repulsions so we would expect a very high stereoselectivity.

As can be seen, this exercise has demonstrated how molecular mechanics can be used to support logical hypotheses of reaction mechanisms to rationalise we we observe certain stereoselectivity.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

This exercise will investigate two characteristics of a precursor to taxol: atropisomerism, and hyperstable alkenes. Atropisomerism arises when the orientation of a particular group, in this case a carbonyl, can change due to rotation of bonds. For the molecule below (labelled 10 and 11), both the atropisomers can interconvert at room temperature, although they are not equally stable. Molecular Mechanics can be used to find which isomer is the more stable and attempt to come up with a reason as to why this might be.

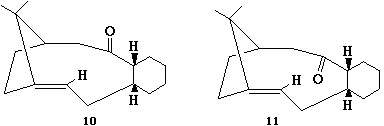
The relative stability of the Atropisomers

Here are the energies found by MM2:

Energy component (kcal/mol)	Carbonyl up	Carbonyl down
Stretch	2.6989	2.5355
Bend	15.5187	10.6515
Stretch-bend	0.2800	0.3196
Torsion	18.0090	19.6790
Non-1,4 VDW	-0.5734	-1.2795
1,4 VDW	12.6442	12.5563
Dipole-dipole	0.2530	-0.1803
TOTAL	48.8303	44.2820

One thing to note is that in order to get the above energies, the cyclohexane component of the molecule had to be manipulated into the chair conformation, as the program had a tendancy of making it a twist-boat. A further minimision then gave the reported energies.

The energies demonstrate that the atropisomer with the carbonyl group pointing down is more stable than the up-facing isomer by 4.5483 kcal/mol. The most significant component of the overall energy which accounts for this difference is the bending strain, which is 4.8612 kcal/mol greater in the up-facing isomer. This suggests that there might be some difference in the bonding angles around the carbonyl carbon between the two molecules, so this will be investigated in the optimised structures. 3D structures for each isomer are shown below.

Carbonyl up:

Taxol first qpzm1029

Carbonyl down:

Taxol second qpzm1029

Where the carbonyl is up, the bond angles around the carbonyl carbon are 118.5^O, 116.4^O and 125.0^O. When the carbonyl is down they are 120.0^O, 119.7^O and 120.2^O, which is very close to the prefered bond angles for an sp² centre. On the other hand, with the bond angles further away from the prefered values, the up-facing isomer experiences greater bond strain, and in turn, destabilises the structure.

We can also look at the 3D structures to provide a qualitative analysis for the relative stabilities of the atropisomers. When the carbonyl points up, we can see that it is very close to on of the hydrogens on the fused cyclohexane ring, resulting is a destabilising 1,3 steric clash. This is probably accounted for by the difference of 0.7061 kcal/mol in the non-1,4 van der waals energies.

Hyperstability of the alkene

It has been observed that the alkene in this taxol precursor reacts more slowly than normal alkenes. Again, we will use MM2 to try and come up with an explanation. Firstly, the most stable atropisomer was hydrogenated and its energy was optimised:

Energy component (kcal/mol)	Carbonyl up	Carbonyl up hydrogenated
Stretch	2.6989	4.6040
Bend	15.5187	23.3937
Stretch-bend	0.2800	1.1294
Torsion	18.0090	19.6790
Non-1,4 VDW	-0.5734	-2.4370
1,4 VDW	12.6442	16.8310
Dipole-dipole	0.2530	0.0000
TOTAL	48.8303	67.9822

It immediately becomes clear that the hydrogenated species is less stable than the alkene as it is greater in energy by 19.0985 kcal/mol. Such alkenes, which cause an increase in energy upon hydrogenation, are refered to as hyperstable. The most significant increase is the bending strain, which goes up by 7.8750 kcal/mol, as well as a noticeable increase of 1.9051 kcal/mol. This is probably down to the fact the the presence of a 10-membered ring makes it very difficuly for the carbon atoms to take up their prefered bond lengths angles and usually makes angles larger then what they would like to be. For this reason, adding a couple of sp² centres into the ring will be favourable because the sp² preferred angle is larger at 120^O as opposed to 109.5 for sp³.

We can see another significant difference in the hydrogenated species upon looking at the 3D structure.

Taxol first hydro qpzm1029

On hydrogenation, one of the added hydrogens adds in such a fashion where it points inside the 10-membered ring. The hydrogen atom being refered to is marked in the image below.

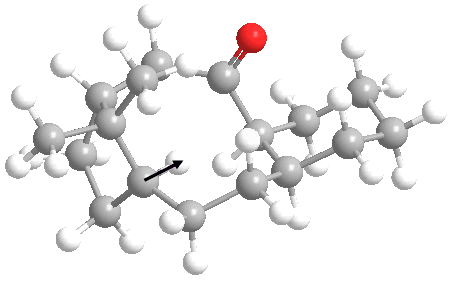
This obviously leads to significant transannular strain as this hydrogen will interact sterically with atoms on the other side of the ring system. This observed transannular strain probably makes a major contribution to the increase of 1.8636 kcal/mol in the non-1,4 van der waals energy.

As we can see, molecular mechanics has confirmed that the hydrogenation of the molecule is associated with an increase in energy and is therefore a thermodynamically disfavoured reaction. Through considering the resulting bond angle and transannular strain, MM2 has provided a viable explanation for the hyperstability of the alkene.

Room Temperature Hydrolysis of a Peptide

This exercise will demonstrate how molecular mechanics can be used to make simple kinetic arguments based on the orientation of groups and relative energies of different conformations. In the hydrolysis of one particular peptide, when we compare two different isomers, one hydrolyses significantly faster than the other. The reaction to be investigated is given below.

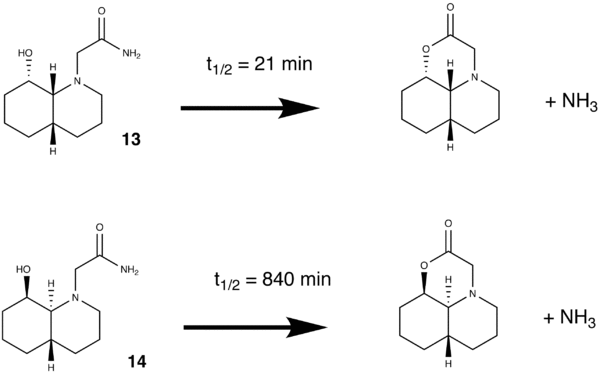
The first course of action was to find the relative energies of each conformation.

Energy component (kcal/mol)	OH down, amide axial	OH down, amide equatorial	OH up, amide axial	OH up, amide equatorial
Stretch	1.6234	1.7015	1.5135	1.4929
Bend	8.1883	5.1416	5.0593	3.5269
Stretch-bend	0.6430	0.5285	0.5456	0.5053
Torsion	12.0709	9.4019	9.0995	8.1558
Non-1,4 VDW	12.0709	-7.3335	-7.0852	-7.7370
1,4 VDW	10.2119	10.0284	9.6281	9.9870
Dipole-dipole	-4.8718	-6.3495	-6.6026	-6.0261
TOTAL	19.8165	13.1189	12.1582	9.9048

Not surprisingly, the conformation with the amide equatorial has lower energy than when it is axial (to avoid 1,3 diaxial compressions) and the trans decalin isomer is more energetically stable than cis decalin (because the OH is axial in cis decalin). In addition, the alcohol and amide groups could be (and were) positioned so that they H-bonded intramolecularly, significantly lowering the energy. However, this doesn't really tell us anything useful about the differing rates of hydrolysis. In order to gain some further clues, we need to look at the 3D structures of the peptide.

OH down, amide axial:

peptide 1 ax qpzm1029

OH down, amide equatorial:

peptide 1 eq qpzm1029

OH up, amide axial:

peptide 2 ax qpzm1029

OH up, amide equatorial:

peptide 2 eq qpzm1029

Since the peptide hydrolysis occurs by attack of the alcohol oxygen (lone pair) on δ+ carbonyl carbon, we should look at the distance between these two atoms in each case. We would expect that when they are closer together the reaction will be faster.

Another aspect which should be considered is the angle of attack of the hygroxyl oxygen on the carbonyl carbon. The closer this is to the Burgi-Dunitz angle (107^O), the better the overlap between the sp³ oxygen lone pair and the C=O π* orbital.

It was also observed (by pressing ctrl-H in ChemBio3d) that there is H-bonding between the hydroxyl hydrogen and the carbonyl oxygen. The level of H-bonding stabilisation will also be considered as stronger H-bonding will more tightly hold the oxygen and carbon atoms together in a possibly reactive conformation.

The following distances, H-bonding and angles were found:

Energy component (kcal/mol)	OH down, amide axial	OH down, amide equatorial	OH up, amide axial	OH up, amide equatorial
O---C distance in angstroms	3.027	2.966	2.923	3.133
OH---C H-bonding in kcal/mol	-4.8718	-6.3495	-6.6026	-6.0261
Angle of approach to C=O in degrees	61.1	66.0	67.7	59.1

It was found that none of the angles of approach match the Burgi-Dunitz angle, although in the OH down/amide equatorial and OH up/amide axial cases, it was a slightly closer match. This might suggest that the attacking sp3 oxygen lone pair was slightly closer to the orientation of the C=O π* orbital. Any attempt made to twist the carbonyl group around the N-C bond broke the H-bonding stabilisation and hence increased the overall energy of the conformation, so the molecule probably would not have twisted around in such a way.

As well as angles closer to the Burgi-Dunitz angles for OH down/amide equatorial and OH up/amide axial, in both of these cases the O--C distances was shorter and the OH---C H-bonding was greater. This means that the hydroxyl oxygen lone pair can more easily attack the δ+ carbonyl carbon (because it is closer to it) and these two atoms (oxygen and carbon) are more strongly held in this reactive conformation.

Using the knowledge we have gained, we can feasibly suggest the following:

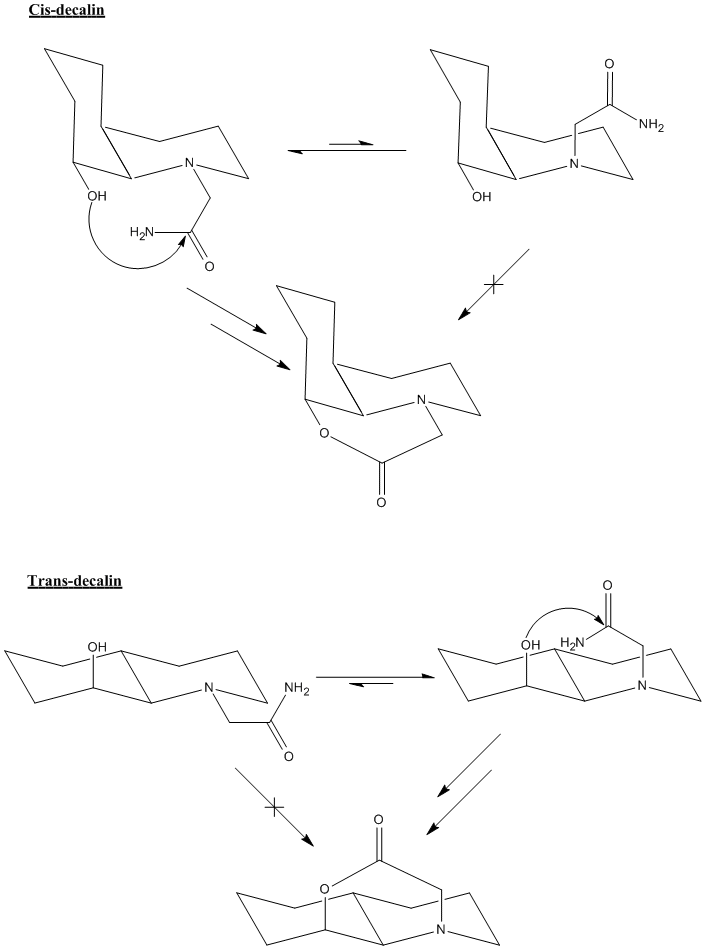
For the first reaction (OH down), the equilibrium lies towards the left as it avoids 1,3 diaxial interactions with the large amide group, so the amide is more commonly found in the reactive, equatorial position.

For the second reaction (OH up), the equilibrium again lies towards the left for the exact same reason, but this time the equatorial amide is not in the reactive conformation. In order to react, the amide needs to be axial and there is less of this conformation present in equilibrium, so the hydrolysis will be much slower than for the first case.

Something else of interest is that peptide hydrolysis usually takes around 500 years, whereas here, it takes mere minutes (for cis decalin). This is most likely down to the fact that most peptides are highly flexible straight chains which have the ability to take up hundreds of different conformations. This means that the probability of finding the alcohol and the amide in a reactive conformation is very low indeed. However, in the reaction being studied here, the alcohol and the amide not only have highly restricted movement due to the fused cyclohexane rings, but are essentially locked into their reactive conformation by intramolecular H-bonding.

Here, we have seen how we can combine molecule mechanics with our knowledge of conformational analysis of cyclohexane to form a logical explanation for the kinetics of certain reactions.

Regioselective Addition of Dichlorocarbene

Up until now, with the exception of the some of the first exercise, we have dealt with each problem using only molecular mechanics i.e. we have not taken into account any effect the electrons in a molecule might have (except for lone pairs). In the following exercise, we will make a transition from pure classical mechanics to quantum mechanics.

The dialkene and its Molecular Surfaces

Addition of dichlorocarbene to the dialkene below can form two possible products as there are two C=C bonds it can add to.

We shall use a quantum mechanical treatment to optimise the structure and calculate it's molecular surfaces in order to examine the prefered site of carbene addition.

Firstly, a standard MM2 optimisation was carried out in order to get a rough approximation of the geometry. Next, a semi-emperical calculation was carried out in order to optimise the structure further and to calculate the molecular surfaces. This was done using the HF (Hartree-Fock) method and STO-3G basis set. Finally, the geometry was was minimised even further and vibrational frequencies were calculated using the more accurate DFT (density functional theory) B3LYP method and 6-31G(d) basis set. This last calculation is fairly intensive and would overheat a laptop computer so it was submitted to the SCAN server and was completed in just under 2 hours.

The optimised structure is shown below.

dialkene qpzm1029

By comparing bonding angles we can take a look at the difference between the accuracy of the 3 methods used. The bonding angle to be compared will be that on the bridgehead carbon between either of the fused ring carbons and the chlorine atom. It was found to be as follows:

With MM2 - 117.6^O

With HF/STO-3G - 122.4^O

With B3LYP/6-31G(d) - 122.7^O

We can see that there is a fairly noticeable difference between MM2 and HF/STO-3G as MM2 does not consider electrons other than non-bonded lone pairs, whereas the semi-emperical calculation does. There is only a small difference between HF/STO-3G and B3LYP/6-31G(d) but the latter method run much slower. However, provided that we can afford the time, the fact that this quantum mechanical method takes into account electron density as well as their probably locations is of significant value as a technique for 'fine tuning'.

The molecular surfaces which were previously calculated are now displayed below.

No orbitals

HOMO-1 : exo C=C π orbital

HOMO : endo C=C π orbital

LUMO : exo C=C π* orbital

LUMO+1 : exo C=C π* orbital

LUMO+2 : C-Cl σ* orbital

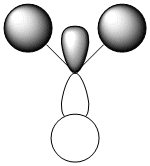
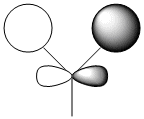
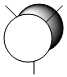
It is clear that the HOMO, the orbital most susceptible to nucleophilic attack, has most of its electron density around the endo elkene so we can predict that this is where addition of dichlorocarbene is most likely to occur.

We can analyse the structure further by looking at the molecular surfaces and seeing if there would be good overlap between any of them. This can be slightly difficult to see as only one molecular surface at a time can be displayed in ChemBio3D, but upon close inspection, it can be seen that due to their anti-periplanar orientations to each other, there would be an in-phase interaction between the HOMO-1 and the LUMO+2, which is the endo C=C π orbital and the C-Cl σ* orbital.

The result is movement of electron density from the π orbital to the C-Cl σ* orbital. The implication of this is a strengthening, and hence shortening of the exo C=C bond, which is 1.332 angstroms and shorter than the endo C=C bond by 0.04 angstroms. With MM2 they are both exactly 1.340 angstroms, so once again, we observe another advantage of DFT calculations over pure classical mechanical treatment.

Another noticeable effect of the mentioned π-σ* overlap is a distortion of the exo C=C bond towards the bridgehead carbon. The distance of the endo C=C bond for the bridghead carbon is 3.284 angstroms, while for for the exo C=C it is 3.029 angstroms. This is a difference 0.255 angstroms.

By combining the increased electron density around the endo alkene with the increased stability of the exo alkene due to π-σ* overlap with the C-Cl anti-bonding orbital, we have demonstrated two factors which predict greater electrophilicity of the endo alkene and thus greater susceptibility to attack by dichlorocarbene.

The Vibrational Frequencies of the Dialkene and Monohydrogenated Alkene

DFT calculations can also be used to predict spectroscopic properties of molecules. For this exercise, we will calculate the IR spectrum of the dialkene and its monohydrogenated derivative by removal (by hydrogenation) of the exo C=C and observe the effect this has on the C-Cl stretching frequency.

First of all, the monohydrogenated derivative has to be modelled and optimised. This was done with the exact same procedure as the dialkene, starting with MM2, then HF/STO-3G, finishing with B3LYP/6-31G(d). The input file submitted to SCAN had the command-line "# b3lyp/6-31G(d) opt(maxcycle=30) freq", which additionally calculated the vibrational frequencies (IR spectrum). An extra point that's worth making is that the dialkene had C_s point group symmetry, but hydrogenation breaks this symmetry so that the new molecule has a C₁ point group. The optimised structure is below.

monohydrogenated qpzm1029

For the dialkene, we would expect to see a lower stretching frequency for the exo C=C compared to endo C=C due to its loss of electron density from its π orbital to the the C-Cl σ* orbital. Upon hydrogenation, we would expect an increase in the C-Cl stretch for the same reason. The calculated frequencies are give below.

Stretch in wavenumbers (cm-1)	Dialkene	Monohydrogenated derivative
C=C	1760.91(endo) and 1740.76(exo)	1760.10(endo)
C-Cl	772.634	776.925

The stretching frequencies match our hypothesis. The C=C stretch at 1760 cm^-1 is clearly due to the exo alkene as it remains largely unchanged in both molecules. The predicted decrease in endo C=C and increase C-Cl stretcheing frequencies are observed and support the qualitative molecular orbital analysis made previously.

This exercise has shown how much of a powerful tool DFT calculations can be with their ability to predict electron density, spectroscopic properties and hence more advanced explanations for selectivity than molecular mechanics was able to provide us with alone.

Mini Project

In the previous exercises, we have shown how computational techniques can be shown to predict characteristics of molecules and reactions. In the mini-project, a (hopefully interesting) reaction will be picked from the literature which gives two possible products and by utilising the techniques already learned, we will attempt determine how we would distinguish between the two products and if possible, find out something new that the people doing the experiment didn't report.

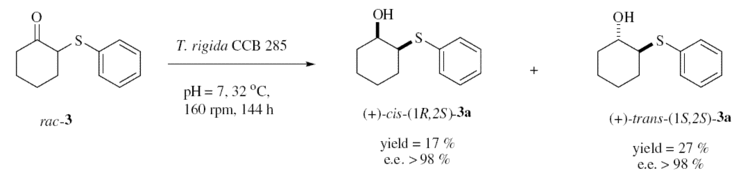
The reduction of (±)-2-(phenylthio)cyclohexanone using whole cells of Trametes Rigida

An area of interest amongst organic chemists is the use of whole cells of micro-organisms to carry out transformations as they can sometimes have certain advantages over the use of synthetic reagents. In this experiment, trametes rigida cells are used to reduce (±)-2-(phenylthio)cyclohexanone. The advantage in using these cells is that they produce only specific enantiomers, whereas reduction with NaBH₄ gives a racaemic mixture.

Before any spectra can be calculated, the first thing to do is to optimise the geometry. The structure was first mimimised with MM2, then HF/STO-3G and finally with an mpw1pw91/6-31(d,p) DFT calculation. The 3D mol file could then be constructed.

Cis isomer:

cis qpzm1029

Trans isomer:

trans qpzm1029

The structures are now ready for spectroscopic analysis.

¹³C NMR Spectra

The first calculation to be run was the predicted ¹³C NMR spectra for both isomers. Once the optimised geometries were retrieved from SCAN, they were re-submitted with the command line "mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)" in order to calculared the ¹³NMR chemical shifts.

The resulting chemical shifts are displayed below.

Predicted ¹³C NMR spectrum of (+)-cis-(1R,2S)-2-(Phenylthio)-1-cyclohexanol

Predicted ¹³C NMR spectrum of (+)-trans-(1S,2S)-2-(Phenylthio)-1-cyclohexanol

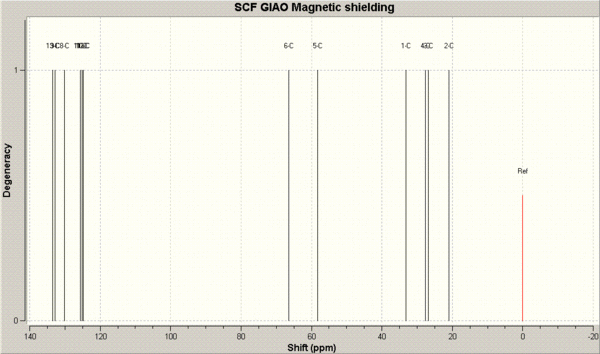
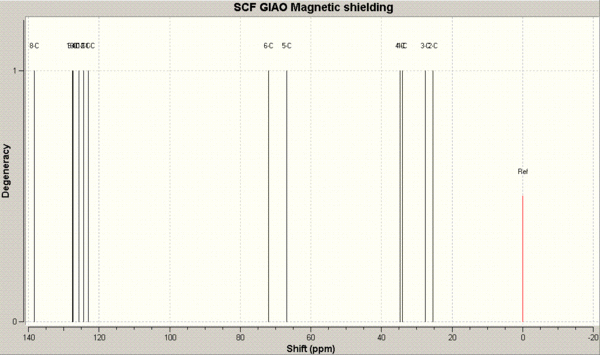
The predicted NMR ¹³C chemical shifts (in ppm) are tabulated below and compared to the literature chemical shifts. The image below the table is for assigning the chemical shifts to the carbon atoms.

Trans - calculated	Trans - literature	Cis - calculated	Cis - literature
138.3 (8)	133.8	133.5 (12)	134.2
127.4 (11)	132.5	132.8 (10)	132.2
127.3 (12)	128.9	130.1 (11)	129.1
125.7 (10)	127.7	125.6 (8)	127.3
124.4 (13)	-	125.1 (9)	-
123.2 (9)	-	124.8 (13)	-
72.0 (6)	72.0	66.4 (6)	67.0
66.6 (5)	56.6	58.2 (5)	54.4
34.8 (2)	33.8	33.2 (1)	31.7
34.0 (3)	32.7	27.6 (3)	27.7
27.6 (1)	26.2	26.8 (4)	24.9
25.5 (4)	24.3	21.0 (2)	20.9

Only the trans isomer is shown here purely for the purpose of labelling the carbons as they are much easier to see. The labels are exactly the same in the cis isomer. The numbers on the carbon atoms correspond to the numbers in the brackets next to the chemical shifts in the above table.

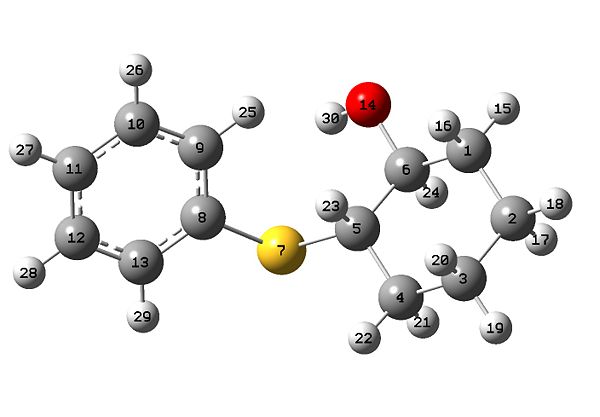
We can see that there is generally a fairly good match between the calculated values. In most cases the calculated values or off the literature by no more than 5ppm. A notable exception is the calculated chemical shift of 66.6 ppm for the trans structre which is 10.0 ppm away from the literature chemical shift of 66.6 ppm. This signal is due to the carbon adjacent to the bridging sulphur atom in the cyclohexane ring.

Unfortunately, the authors of the article have not assigned their ¹³C chemical shifts so we cannot compare these to the assignments made by the DFT calculation.

The literature has ommitted a couple of values for each isomer, although this is clearly due to the fact that the chemical shifts around this area (for the benzene carbons) are very close together so the group of 3 peaks probably only appeared as 1 to the chemists who analysed the spectra.

³J_H-H Coupling Constants

Due to the presence of equatorial and axial protons in the cyclohexane ring, ³J_H-H coupling constants are probably the most useful piece of information for distinhuishing between the two isomers. We can take advantage of the fact that in the trans isomer, the proton attached to same carbon as the hydroxyl is axial, whereas in the cis isomer, this proton is equatorial. Due to dihedreal angles near to 180^O for axial-axial couplings, we would expect to see much larger coupling (due to the Karplus equation) than for the equatorial-equatorial or equatorial-axial couplings in the trans isomer.

The ³J_H-H coupling constants were calculated by loading the mol files of the two isomers into the Janocchio program which, by finding dihedral angles between protons, uses a form of the Karplus equation to estimate coupling constants. The found constants are tabulated below.

Cis isomer:

Protons coupling	Type of coupling	dihedral angle (degrees)	3JH-H coupling constant
Ha- Hb	equatorial-axial	57.1	1.95 Hz
Ha- Hc	equatorial-equatorial	53.6	2.68 Hz
Ha- Hd	equatorial-axial	62.4	3.53 Hz

Trans isomer:

Protons coupling	Type of coupling	dihedral angle (degrees)	3JH-H coupling constant
Ha- Hb	axial-axial	178.7	9.85 Hz
Ha- Hc	axial-equatorial	62.1	3.81 Hz
Ha- Hd	axial-axial	177.7	11.42 Hz

As predicted, the coupling constants for the trans isomer are a great deal larger as the two 9.85 Hz and 11.42 Hz values are typical for axial-axial couplings in cyclohexane rings. The couplings between the same protons in the cis isomer are much smaller, so we have a clear way of telling apart the two isomers.

Unfortunately, the authors of the article have not given any ³J_H-H coupling constants of their own as all the ¹NMR signals have been reported as multiplets. However, it would be interesting to see how well the calculated coupling constants would compare with the experimental values should the same or a similar experiment be analysed with an NMR spectrometer with a greater field strength, such as the very large 800MHz machines for instance.

IR Spectra

The IR spectra were calculated by using the optimised geometries and re-submitting to SCAN with the command-line "# b3lyp/6-31G(d,p) opt freq".

The resulting IR spectra are below.

Predicted IR spectrum of (+)-cis-(1R,2S)-2-(Phenylthio)-1-cyclohexanol

Predicted IR spectrum of (+)-trans-(1S,2S)-2-(Phenylthio)-1-cyclohexanol

The two spectra are very similar so aren't very useful for discriminating between the two isomers. Clearly, the ¹³NMR spectra and ³J_H-H coupling constants is the most useful information for this purpose.

Optical Rotary Power

Both products are optically active with high enantiomeric excess so we can calculate the optical rotary power to compare it the values reported in the literature.

Again, the optimised geometries were re-submitted to SCAN, but this time with the following command-line "# b3lyp/aug-cc-pvdz polar(optrot) scrf(IEFPCM,solvent=dichloromethane)". The optical rotary powers were found to be:

[α]D in degrees	Calculated	Literature
Cis compound	+20.71	+19.7
Trans compound	+74.33	+61.0

Even though predicted optical rotation tends not to be so accurate for angles less than 100 degrees, the matches here are surprisingly good and togther with the ¹³NMR spectrum, provides a fairly conclusive distinction between the cis and trans isomers.

Relative Yields of the Isomers

The yields of both isomers are quite low, but the trans isomer is produced in a slightly higher yield (27% as opposed to 17% for cis), showing that this strucutre is slightly favoured over the cis isomer. The authors of the article have stated this in their report, but have not attempted to explain the reason for this.

An attempt to use molecular mechanics to explain this resulted in the trans isomer being the more stable product by 0.6921 kcal/mol (3.1904 - 2.4983). This means that it is the thermodynamic product, which is consistent with what is observed in the experiment.

This could be the only reason for the slight difference in relative yeilds, however, in case there is a kinetic factor as well, the molecular surfaces of the ketone precursor were calculated. This was done by first minimising the ketone with MM2, then HF/STO-3G and finally minimising and calculating the orbitals with B3LYP/6-31G.

Before we start talking about the orbitals, something interesting was found during the MM2 minimisation of the ketone. Here are the structures:

Ketone with equatorial sulphide

Ketone with axial sulphide

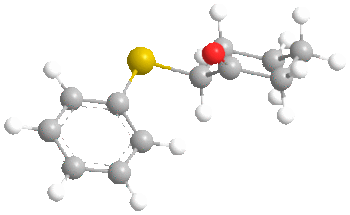
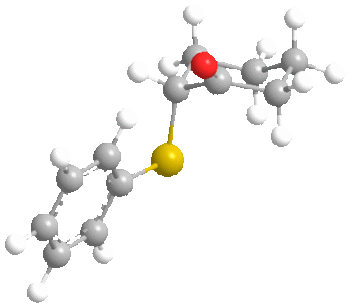
FIrst of all, it is clear that in both conformers, the carbonyl oxygen points up. However, the interesting point is that molecular mechanics found the most stable conformer of the ketone to be the one with the sulphide group axial rather than equatorial as we would usually expect. This was by 0.8772 kcal/mol (6.5711 - 5.6939). A possible reason for this is the length of the C-S bond, which is 1.807 angstroms. This large bond length probably decreases the effect of 1,3 diaxial interactions with axial hydrogens as the sulphur atom is further from the cyclohexane ring than normal. It probably goes axial to increase the distance between the phenyl and the cyclohexane to 3.233 angstroms, compared to 2.369 angstroms in the equatorial case. This may prove to have an effect on the ratios of stereochemistry later on.

We will now consider the molecular surfaces of the ketone:

Equatorial sulphide - C=O π* orbital - LUMO+2

Axial sulphide - C=O π* orbital - LUMO

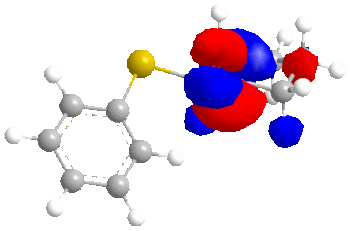
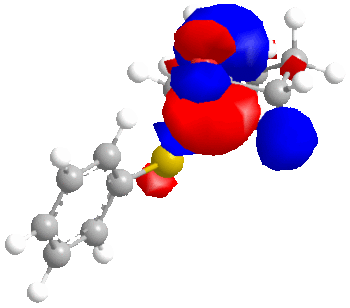
As can be seen from the structures without molecular surfaces included, the reducing agent must approach the carbonyl carbon from below, due to the up-facing oxygen.

For the axial sulphide case, once the carbonyl has been reduced to an alcohol, the cyclohexane will probably ring flip to put the sulphide group equatorial, as this is the most stable conformation for the reduced product (by 0.6921 kcal/mol as shown earlier). In the process of ring flipping, the alcohol group will now point down, and the end result will be the trans product.

For the equatorial sulphide case, the reducing agent (the T. rigida cells) will once again approach from below, but as the sulphide group is already equatorial (and up facing) there will be no ring flipping of the cyclohexane. The end result this time will be a cis product.

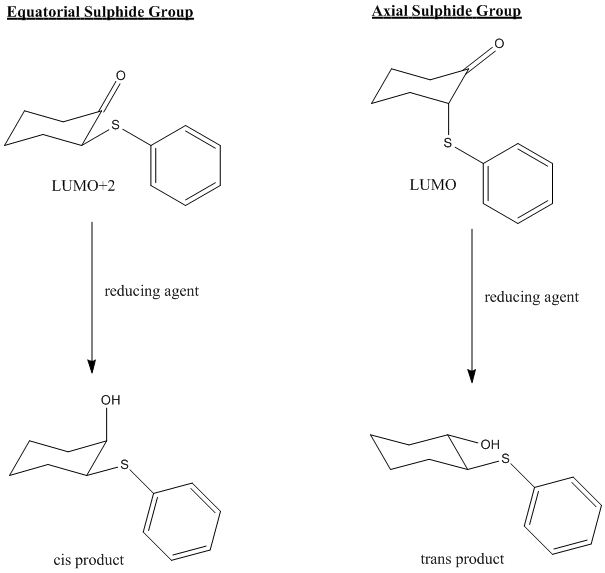
Now, the important point, is that in the equatorial sulphide case (still talking about the ketone), the C=O π* orbital is the LUMO+2, whereas for the axial sulphide case, it is the LUMO, which is lower in energy and will therefore be more accessible to a nucleophile. Greater susceptibility to nucleophiles will lead to a slight increase in the rate of reaction and ultimately a greater yield compared to the ketone with an equatorial sulphide.

This can all be illustrated with the diagram below:

Of course this model only considers the characeristics of the ketone/alcohol and completely neglects the structure of the T. rigida cells, which are completely unknown at this point. However, this is out of the scope of the techniques used in this experiment. Nevertheless, we have suggested an explanation for the small degree of selectivity in this low yield reduction by incorporating both classical mechanical and quantum mechanical treatments.

Conclusion

This mini-project has demonstrated how computational techniques can be used to not only characterise compounds and distinguish between isomers, but also to rationalise stereoselectivity by using both molecular mechanics and DFT calculations in order to combine both a thermodynamic and a kinetic picture. It is abundantly clear just how much of a powerful tool chemists have at their disposal in computational chemistry.

Note to marker: for some reason the jobs on the SCAN webpage would not publish but simply gave an error stating "Error - You cannot publish this job" despite the fact the the calculations themselves were successful. as shown in the screenshot below.