Rep:Mod:pv=nrt3
Module 3
Optimisation of the Reactants and the Products
1,5 hexadiene was shown to have an energy of -231.6926a.u. after optimisation with the method HF/3-21G, when the initial geometry had the 4 central carbon atoms arranged anti (the same structure as anti1 on appendix 1). The point group of the molecule was C2 after the calculation. With the 4 central carbon atoms gauche, the energy after optimisation was -231.6892a.u., with the point group of the resultant conformation being C1 (gauche5). Optimisation with the same calculation method was repeated for other versions of the same molecule, whereby the 4 central atoms were anti but the angle at which the C=C bonds were orientated with respect to the rest of the molecule was different. The anti-2 conformation, which belonged to the point group Ci, was shown to have an energy of -231.6854a.u. and its point group after optimisation was C1 (presumably the optimisation process turned the molecule assymetric).
 |
 |
The molecule was drawn on the Gaussian with the conformation as similar as possible to the "gauche 3" on the manual (since that was the lowest energy conformation on appendix 1) and was optimised. The resultant energy was -231.69266a.u. (5 decimal places), which is in good agreement with the value on appendix 1. The anti2 conformer, belonging to the Ci point group, was shown to have an energy of -231.69254a.u. (to 5 decimal places). Optimisation by DFT/6-31G(d) method changed its energy to -234.61171a.u., implying a change in energy of 7664.3kJmol-1 (!). After this second optimisation, the two C=C bonds were both inclined at an angle of 118.5° (to the nearest 0.1°) with respect to the central C-C bond, whereas the geometry after the first optimisation had the two C=C inclined at 114.7°, in other words after the second optimisation the molecule was slightly closer to being flat or planar.
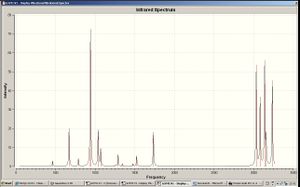
The vibrational frequencies of this molecule was calculated using the same calculation method and basis set. The sum of electronic and zero-point energies, the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies and the sum of electronic and thermal free energies were -234.469196, -234.461850, -234.460906 and -234.500770 Hartree per particle respectively.
 |
Optimisation of the "Chair" and "Boat" Transition State Structures
An allyl group (CH2CHCH2) was optimised on the gaussian using the HF/3-21G method, then two copies of it were loaded on a new page and re-orientated to build a model of the chair transition structure for the (3,3) sigmatropic rearrangement of 1,5 hexadiene. The distance bewteen the terminal carbon atoms (the carbon atoms between which the bonds were to form and break) were 2.11983 and 2.16523Å. After the Gaussian optimisation to Berny (and calculation of the vibrational frequencies) those two distances were both 2.01975Å. One of the vibrational modes was shown to be an "imaginary" one, with a wavenumber of -817.9cm-1. With the other optimisation method (the frozen coordinate method) the distances between the terminal carbon atoms were set to be 2.200Å.
Unfortunately the calculation method using the "freezing" of coordinates did not work successfully.
For the boat structure of the transition state, the QST2 method was used, whereby the structures of the diene before and after the rearrangement were drawn and the program was ordered to analyse the highest energy structure that lay in between the conversion of the two.
 |
 |
 |

The structures optimised by HF/3-21G method were re-optimisd using B3LYP/6-31G(d).
Energy values (a.u.) calculated by HF/3-21G
| molecule | Eelec | Σ(Eelec + Ezero-point) | Σ(Eelec + Ethermal) |
|---|---|---|---|
| reactant(Ci, anti2) | -231.69254 | -231.53954 | -231.53257 |
| Chair Transition State | -231.61519 | -231.46380 | -231.45816 |
| Boat Transition State | -231.60280 | -231.45093 | -231.44530 |
Energy values (a.u.) calculated by B3LYP/6-31G
| molecule | Eelec | Σ(Eelec + Ezero-point) | Σ(Eelec + Ethermal) |
|---|---|---|---|
| reactant(Ci, anti2) | -234.61171 | -234.46920 | -234.46185 |
| Chair Transition State | -234.55407 | -234.41340 | -234.40710 |
| Boat Transition State | -234.54309 | -234.40234 | -234.39600 |
| reaction | Ea @ 0K | Ea@298.15K |
|---|---|---|
| To Chair TS (HF/3-21G) | 198.86 | 195.36 |
| To Boat TS (HF/3-21G) | 232.66 | 229.13 |
| To Chair TS (6-31G(d)) | 147.28 | 143.74 |
| To Boat TS (6-31G(d)) | 175.53 | 172.87 |
According to the HF/3-21G method, the boat structure of the transition state is 33.80kJmol-1 higher in energy than the chair conformation at 0K and 33.77mol-1 higher at 298.15K. The 6-31G(d) method states that the boat conformation is 28.25kJmol-1 higher in energy than the chair at 0K and at 298.15K 29.13kJmol-1 higher. The two methods disagree in the sense that the HF/3-21G the vibrational energy of the chair conformation is higher than that of the boat, whereas the other method suggests the opposite to be the case.
| structure | terminal carbon-carbon distance |
|---|---|
| chair TS (guess) | 2.11983, 2.16523 |
| chair TS (optimised) | 2.20000, 2.20000 |
| boat TS (optimised) | 2.20696, 2.20696 |
IRC Analysis
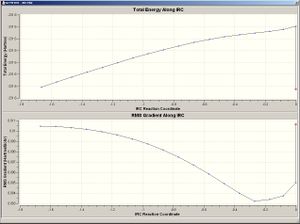
IRC analysis was done on the boat transition structure, with N=50. 2.20696Å was the distance between the two terminal carbon atoms (in both termini). The minimum was not reached, however, and so the IRC was repeated by i) increasing N into 200 and ii) taking every force constant into calculation. When every force constant was calculated, the
 |
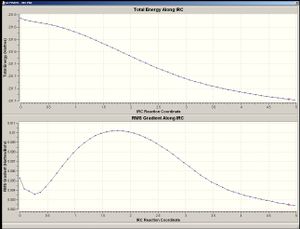 |
Diels-Alder Cycloaddition
Cis-butadiene was optimised using the HF/3-21G method. The resultant final energy was -154.05394a.u., with the two C=C-C angles of 126.7°, which is slightly greater than a C=C-H angle in ethene (which should be 120°).
 |
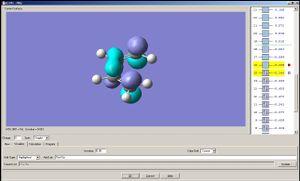 |
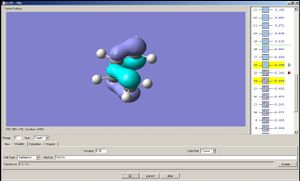
The HOMO of cisbutadiene is assymetrical with respect to a mirror plane that divides the molecule into halves; the LUMO is symmetric.
The transition state of the Diels-Alder cycloaddition between cis-butadiene and ethene (both optimised by the same HF/3-21G method; the C=C bond length in ethene changed from 1.32592 to 1.31508Å after optimisation). The "Berny" method was used to analyse the transition state; the input data was sent to SCAN (since time was running out). The vibrational frequency data of the resultant transition state structure showed that oen of the vibrational modes was an "imaginary" one, with a wavenumber value of -818.163cm-1.
Lengths of key bonds (Å)
| molecule (optimised) | the C-C between which the σ new bond forms | C=C of butadiene | C=C of ethene |
|---|---|---|---|
| ethene | N/A | N/A | 1.31508 |
| cis-butadiene | 1.47909 | 1.32007, 1.32007 | N/A |
| Transition State | 1.39462 | 1.36999, 1.36999 | 1.37586 |
(The lengths of the σ bonds about to be formed were 2.20946 and 2.20969Å.)
The fact that the C=C bond of ethene is elongated suggests the decrease in bond order (in otherwords, it has less double bond character in the transition state). The same applies to the C=C bonds of butadiene, and the opposite for the C-C at the centre of the butadiene (the shortening of the bond suggests an increase in bond order, i.e. a build up of π electron density).
Values of energy (a.u.)
| molecule (optimised) | ETOT | ∑(Ezero-point + electronic) | ∑(Ethermal + vibrational) |
|---|---|---|---|
| ethene | -77.60099 | -77.545896 | -77.542938 |
| cis-butadiene | -154.05394 | -153.962203 | -153.958420 |
| Transition State | -231.60321 | -231.451339 | -231.445651 |
The transition state was shown to have one "imaginary" vibrational mode, with a wavenumber of -818.2cm<sip>-1.
From the energy values obtained above, it follows that Ea = 149.0kJmol-1 at 0K and 146.3kJmol-1.
 |
 |
The HOMO and the LUMO of the transition state are both symmetrical with respect to the mirror plane bisecting the molecule.
| molecule | HOMO (eV) | LUMO (eV) | |
|---|---|---|---|
| ethene | -0.402 | -0.165 | |
| cis-butadiene | -0.366 | -0.208 | |
| Transition state | -0.366 | -0.197 |
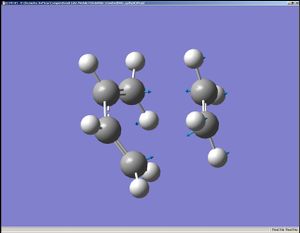
For the Diels-Alder reaction between 1,3 cyclohexadiene and maleic anhydride, the transition states leading to the endo and exo products were both examined.
| molecule | C-C (where the π bond forms) | C=C of the hexadiene | C=C of the anhydride |
|---|---|---|---|
| 1,3 cyclohexadiene | 1.47562 | 1.32212, 1.32212 | N/A |
| maleic anhydride | N/A | N/A | 1.31583 |
| exo-TS | 1.37543 | 1.39062, 1.39062 | 1.39787 |
| endo-TS | 1.39608 | 1.37092, 1.37091 | 1.37032 |
(The distance between the two carbon atoms at each termini where the new bonds were forming were 2.19056 and 2.19049Å in the exo-version and 2.23083 and 2.23083Å in the endo version).
| molecule | ETOT | ∑(Ezero-point + electronic) | ∑(Ethermal + vibrational) |
|---|---|---|---|
| 1,3 cyclohexadiene | -230.54323 | -230.411186 | -230.406354 |
| maleic anhydride | -375.10351 | -375.042900 | -375.038067 |
| exo-TS | -601.24871 | -601.036594 | -601.028657 |
| endo-TS | -605.61037 | -605.414907 | -605.405482 |
Interestingly, the vibrational frequency data of the exo-transition state gave three "imaginary" peaks, at 1077.42, 67.4524 51.347cm-1. The endo-version gave an imaginary vibrational frequency at -644.12cm-1.
 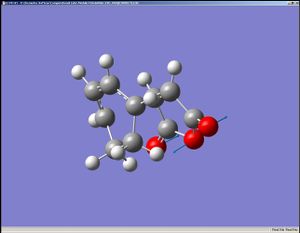 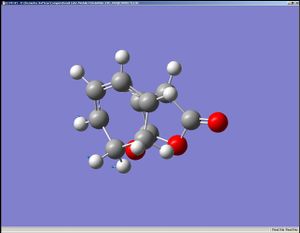 |
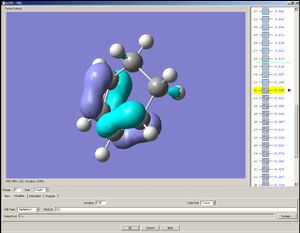 |
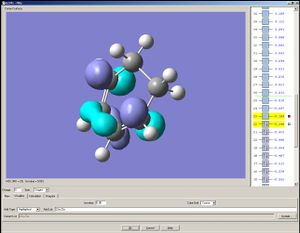 |
The HOMO is assymetric with respect to the mirror plane and the LUMO symmetric to it.
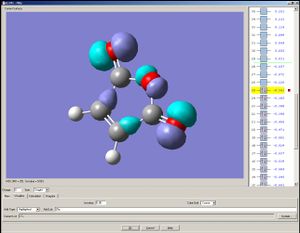 |
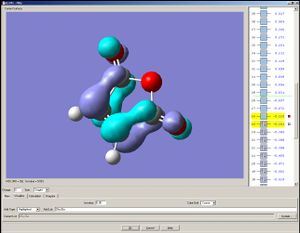 |
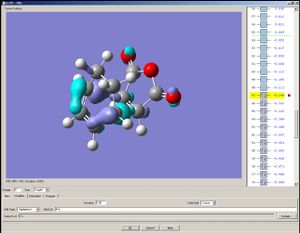 |
 |
 |
 |
The HOMO and the LUMO are both assymetrical with respect to the mirror place. Please note that the HOMO are more localised than that of the transition state of the previous Diels-Alder reaction observed (presumably because the transition state here contains three oxygen atoms, which are more electronegative than carbon).
| molecule | HOMO (eV) | LUMO (eV) | |
|---|---|---|---|
| 1,3 cyclohexadiene | -0.348 | -0.199 | |
| Maleic Anhydride | -0.361 | -0.220 | |
| exo-TS | -0.349 | -0.211 | |
| endo-TS | -0.346 | -0.206 |
References
1. en.wikipedia.org
