Rep:Mod:pv=nrt2
Module 2
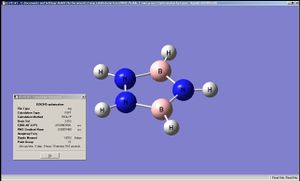
BH3
In this exercise a BH3 molecule was optimised using the B3LYP/6-31G method, followed by the acquisition of data of its vibrations and molecular orbitals. The BH3 molecule was shown to have a symmetry of D3h after optimisation; the B-H bond lengths were all 1.19435 Angstroms, H-B-H angles were all 120 degrees and the final energy was -26.46226438a.u.
N.B. The bending motions are lower in energy than the stretching ones, since in stretching vibrations the nuclei are pulled away from the equilibrium positions.
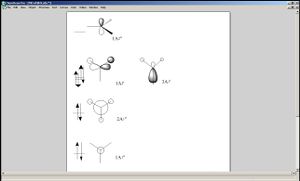
Now let us observe the molecular orbitals of BH3: (please note, BH3 on the chem draw diagram was looked at with a bird's eye view, with the z-axis coming out of the plane. The exception is the image of the LUMO, which was looked at from the side to clarify the fact that it is orthognal to the plane of the molecule, and the z-axis is pointing upwards).
 |
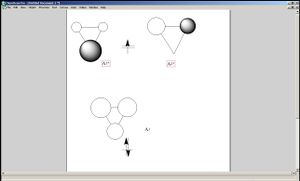 |
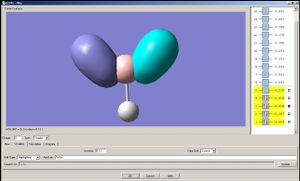
The A1 bonding orbital of H3 combines with the 2s atomic orbtial of the boron, which also has A1 symmetry (the 1s of boron is too low in energy to interact with the H3 fragments). The A1* antibonding orbital of H3 combines with a 2px (or 2py depending on which way the axes are labelled) orbital of boron to generate an A1 molecular orbital, and finally the A2* fragment from the H3 combines with the 2py of the boron (or 2px if the axes are labelled vice-versa). The 2pz orbtial of boron is left untouched since there is no fragment on H3 with the same symmetry label.
| 1A1' | 2A1' | 1A2' | 1A1 | 1A2 |
|---|---|---|---|---|
 |
 |
 |
 |
 |
One difference between the estimated shape of the molecular orbitals and the calculated ones is that when atomic orbitals of each atom contributes to a molecular orbials, in the estimated ones, the orbitals are represented as a set of fragments which are confined to certain atoms of the molecule, whereas in the case of the calculated ones the whole orbital is spread out over the entire molecule.
BCl3 - Comparison with BH3
Geometry optimisation was repeated for BCl3, which also belong to the D3h point group. After optimisation the Cl-B-Cl angles were all 120°, but the B-Cl distances were all 1.86592Å, which is longer than 1.19435Å (the B-H distance in BH3 after optimisation). The difference in these bond lengths arise since in BCl3 the Cl atoms have lone electron pairs which would repel each other in close distances. However with BCl3 the calculation method was done with a basis set LANL2MB instead of 3-21G which was used in the case of BH3. The calculation time was 15.0sec, which was 19.0sec for BH3. The final energy was -69.4393 a.u. which, for BH3, was -26.4623 a.u. (to 4 decimal places). The reason for the difference in energy accounts for the fact that there is in BCl3 there is some interaction of the lone p electrons of the Cl with the vacant p orbtial of Boron (which causes thermodynamic stability). Furthermore, the Cl atoms are bulkier than H atoms, therefore it is more difficult for nucleophiles to approach the B atom (kinetic stability). The file type, calculation type, calculation method and the dipole mement of BCl3 was .log, FOPT, RB3LYP and 0.0000D respectively, which were identical to those of BH3.
An Analysis of a Small Molecule of Choice (SiO2)
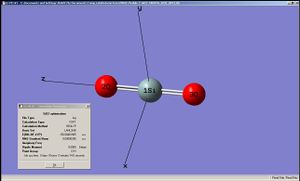
SiO2 was chosen to be the molecule for a short analysis by B3LYP/6-31G method. The bond angle O-Si-O was 180 (as can be seen from the x and y coordinates of the two oxygen atoms.
| Centre Number | Atomic Number | Atomic Type | x-coordinate | y-coordinate | z-coordinate |
|---|---|---|---|---|---|
| 1 | 14 | Si | 0.000000 | 0.000000 | 0.000000 |
| 2 | 8 | O | 0.000000 | 0.000000 | 1.610400 |
| 3 | 8 | O | 0.000000 | 0.000000 | -1.610400 |
The LUMO of the molecule is an antibonding combination of the 3s orbital of Si and the 4σ orbtial of O(sub>2. The fact that the LUMO is predominantely on the Si implies that any nucleophilic attack on the molecule will be done on the Si atom. SiO2 is isoelectric with CO2 but since C and O are both in row 2 of the periodic table and Si in the third row, the orbital overlaps between Si and O is expected to be poorer than those between C and O. This means that the LUMO of the molecule will be more concentrated on Si than it is for C (in CO2 the moleular orbitals would have the tendency to be more spread out over the entire molecule) which would make Si in SiO2 more thermodynamically susceptible to nucleophilic attacks than the C in CO2 (in addition to the fact that nucleophiles would find it kinetically easier to attack the silicon because of its larger atomic size compared to carbon).
 |
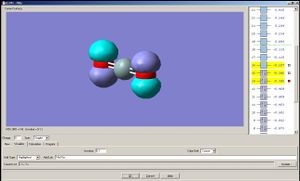 |
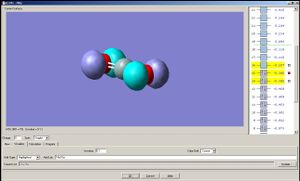 |
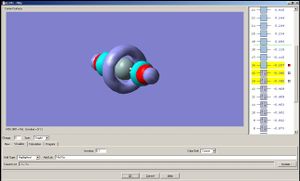 |
NH3
Optimisation of NH3 was done by B3LYP/6-31G method for 3 different initial geometries. The first one had all the N-H bonds with a length of 1.00Å, with H-N-H angles of 109.47120, 109.47120 and 109.47125°. The geometry after the optimisation was C3v. The second one was slightly modified from the first in that one of the N-H bonds with a length of 1.01Å with the other two 1.00Å. The resultant geometry was C1v. Finally an NH3 with a planar structure was optimised, with the resulting point group being D3h.
 |
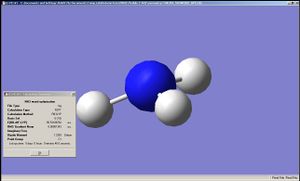 |
 |
The times of calculation were 26, 46 and 75 seconds respectively; it seems as though high symmetries require a relatively long time for calculation.
The final energies of the 3 versions of NH3 were -56.53188590, -56.53188762 and -56.53154189a.u. respectively - it turnes out that the C1 version is the lowest in energy.
The C3v and D3h versions are 4.516 × 10-3kJmol-1 and 0.908 × kJmol-1 higher in energy than the C1 version (!), respectively (1 a.u. = 4.35974417 × 10-18J[2]). The former energy difference is not significant but the latter is, since the Arrhenius equation states that the rate k of a reaction equals
Ae-Ea/RT and at room temperature (298.15K) RT equals 2.479kJmol-1.
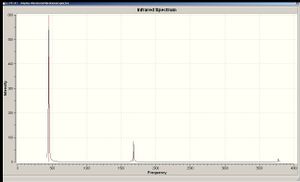
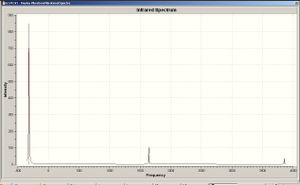
The C3v version of NH3 has 6 positive vibrational modes, whereas the D3h version has 5 positive ones and one negative, which is a bending motion. This is the motion that corresponds to the inversion of the normal (pyramidal) NH3 molecule via the higher-energy D3h (which corresponds to the transition state). The reason why this mode is given a negative frequency value is that by bending the molecule and turning its geometry from planar to pyramidal, the energy of the molecule is reduced. Normally the initiation of vibrational modes requires an input of energy since nuclei are being forced to move away from its equilibrium position (in bending motions; in stretches, the displacement of bonding electrons from its equilibrium position is also forced). Here the initial planar geometry was relatively high in energy to begin with and the movement of the nuclei into its equilibrium position lowered the overall energy of the molecule.
 |
 |
Energy optimisation of NH3 was repeated with different calculation methods to see the effect. A C3v version, when optimised using the MP2 method, took 31sec. to complete the job and showed a final energy of -56.434a.u., and the D3h verison took 36sec. on MP2 with a final energy of -56.4267a.u. Hence the difference in energy between C3v and D3h is 18.4kJ-1, significantly higher than the difference in energies bewteen the three different geometries of the molecule calculated by B3LYP.
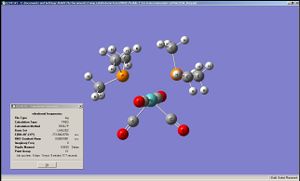
Cis and Trans Isomerism
In this exercise cis and trans isomers of Mo(CO)4(P(CH3)3)2 had their geometry optimised by B3LYP/LANL2MB method followed by B3LYP/LANL2DZ and their IR frequencies were obtained.
 |
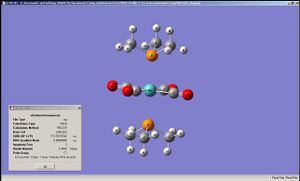 |
| bond (Å) | Cis-Mo(CO)4(P(CH3)3)2 | Cis-Mo(CO)4(P(CH3)2Ph)2 [1] | Cis-Mo(CO)4(P(CH3)Ph2)2 [1] |
|---|---|---|---|
| Mo-P | 2.65092, 2.64823 | 2.525, 2.533 | 2.545, 2.565 |
| Mo-C | 1.98294, 1.98124, 2.03237, 2.03233 | 1.981, 1.983, 1.997, 2.034 | 1.981, 1.975, 2.022, 2.031 |
| C-O | 1.19128, 1.19237, 1.18798, 1.18803 | 1.150, 1.163, 1.150, 1.125 | 1.153, 1.152, 1.141, 1.148 |
| P-C | 1.89607, 1.89040, 1.89039, 1.89295, 1.89290, 1.88983 | 1.837, 1.862, 1.819, 1.836, 1.863, 1.815 | 1.841, 1.826, 1.842, 1.840, 1.837, 1.841 |
(The relativly long Mo-C bonds are the ones that are orthognal (nearly) to the Mo-P bonds)
| angle (°) | Cis-Mo(CO)4(P(CH3)3)2 | Cis-Mo(CO)4(P(CH3)2Ph)2 [1] | Cis-Mo(CO)4(P(CH3)Ph2)2 [1] |
|---|---|---|---|
| P-Mo-P | 95.40561 | 94.78 | 92.52 |
| P(1)-Mo-C | 89.64244, 178.50822, 88.53230, 88.70481, 86.08363, 174.95081, 89.84715, 89.56495 | 87.1, 175.5, 89.3, 87.8, 89.7, 176.3, 94.0, 87.0 | 92.9, 178.5, 90.6, 88.9, 87.8, 172.2, 88.8, 95.8 |
Trans-Mo(CO)4(P(CH3)3)2
| bond | distance (Å) |
|---|---|
| Mo-P | 2.57196, 2.57197 |
| Mo-C | 2.02891, 2.02877, 2.02891, 2.02877 |
| C=O | 1.18988, 1.18988, 1.18988, 1.18988 |
| angle | degree (° ) |
| P-Mo-C | 91.25396, 90.61397, 88.73292, 89.40006, 88.74733, 89.38630, 91.26579, 90.59967 |
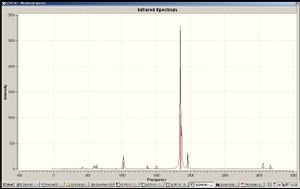 |
 |
| vibration | cis | trans |
|---|---|---|
| P-C stretch | 1019 | 1018 |
| CO assymetric stretch | 1848 | 1839 |
| CO assymetric stretch | 1850 | 1839 |
| CO symmetric stretch | 1870 | N/A |
| CO assymetric stretch | 1960 | N/A |
In Mo(CO)6, the Mo-C distance is 2.06Å[5] which is significantly longer than the Mo-C distances for the complex obtained here. This suggests a considerable backbonding (donation of π electrons from the metal d-orbital to the π* of the CO) taking place (in other words, the bond order of Mo-C is increased, and hence the Mo-C distance shortens. The back-bonding ability of Mo is related to the nature of the phophine ligand, which itself is capable of π donation (and so making the metal electron rich). The replacement of a methyl group by a phenyl group does not seem to have a significant effect on the extent of backbonding from the metal to the CO. The trans isomer has less vibrational peaks shown on the spectrum, since a vibration has to change the overall dipole moment of the molecule if it were to be observed. The energy of the cis isomer after the second optimisation was shown to be 7.88kJmol-1 lower than that of the trans isomer, which is nearly ten times as small as the literature value of 72.98kJmol-1[3](but in the right direction). In order to favour the production of the trans isomer, one may use a bulkier substituent in place of the trimethyl phosphine used, or alternatively the complex could be formed with the same ligands but with smaller metal centres (which would bring the ligands closer together, increasing the steric repulsions between them). If cis-isomer is the one that is preferred, the favour towards it can be increased by the introduction of a bidentate ligand (to coordinate to two sites on the Mo which are cis to each other).
Job ID of the calculations done on SCAN for this exercise: 10052, 10053, 10164, 10166, 10332, 10333
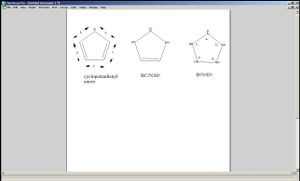
Mini Project: Derivatives of Cyclopentadienyl Anion
Metal complexes with cyclopentadienyl anions have been used widely in organometallic chemistry - but what use could one make of their isoelectric analogues? A Ruthineum tricarbonyl complexed to a BCH3C2N(tert.butyl)2H5 compound has been reported by Schmid in 1981[5]. Another possible five-membered cyclic ring would be B2N3H5 - also containing 6 electrons. The purpose of this experiment is to investigate the nature of these analogues of cyclopentadienyl anion and to see the effect of their presence in transition metal carbonyl complexes.
 |
 |
 |
The geometry optimisation of these three compounds were all done by B3LYP/3-21G, since they were all relatively small molecules made of light atoms.
| bond (Å) | Cyclopentadienyl anion | BC2N2H5 | B2N3H5 |
|---|---|---|---|
| a | 1.42006 | 1.44516 | 1.45452 |
| b | 1.42003 | 1.44526 | 1.45446 |
| c | 1.42004 | 1.41296 | 1.42711 |
| d | 1.42005 | 1.41290 | 1.42715 |
| e | 1.41998 | 1.35646 | 1.44976 |
| angle ( ° ) | |||
| a | 108.00 | 103.27 | 109.92 |
| b | 108.00 | 109.59 | 105.98 |
| c | 108.00 | 109.58 | 105.98 |
| d | 108.00 | 108.78 | 109.06 |
| e | 108.00 | 108.78 | 109.06 |
The N-B distance in borazine (B<su>3N3H6) is 1.44Å[2] and those of B2N3H5 are in good agreement - therefore one may assume this five-membered compound to be "aromatic" (n+2 electrons do not necessarily contribute to aromaticity).
 |
 |
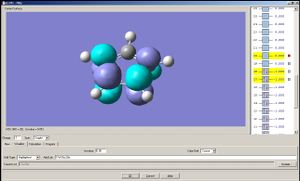
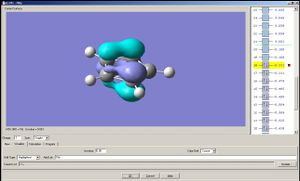
Note: A cyclopentadienyl anion has two degenerate HOMO's and two degenarate LUMO's; the two analogues compounds studied here do not have such degeneracies. The HOMO a) of the cyclopentadienyl anion may overlap with px and dxz orbital of the metal, and the HOMO b) with py and dyz. The LUMO a) may overlap with dx2-y2 of the metal and LUMO b) with dxy[4].
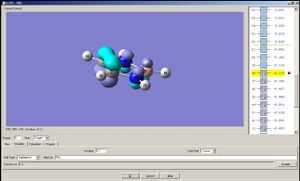 |
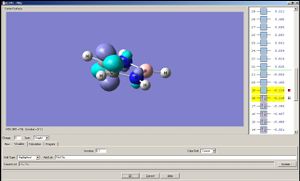 |
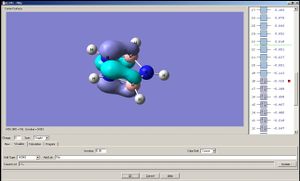 |
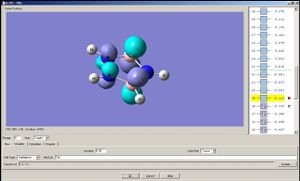 |
In the two analogous compounds the HOMO may overlap with the px and dxz orbital of the metal, and the LUMO with dxy.
The geometry of the iron complexes of these ligands were examined by performing optimisation first on LanL2MB then on LanL2DZ, since here the analytes were far larger. Interestingly ferrocene was shown to have an staggered conformation when optimised by LanL2MB but LanL2DZ produced the eclipsed conformation. The complexes of the other two ligands showed staggered conformation after LanL2DZ and belonging to C2 point group. The BC2N2H5 and B2N3H5 had their rings bent, rather than planar, when complexed to Fe, Co and Ru (in all cases it was ensured that the metal complexes each had 18 valence electrons on the metal centre). This implies that "aromaticity" in these analogues of cyclopentadiene were weaker than that of cyclopentadiene itself (presumably due to differences in sizes of the p-orbitals).
| complex | Distance between the metal centre and the nearest atom (of the ring), Å |
|---|---|
| ferrocene | 2.12004 |
| Fe(BC2N2H5)2 | 2.13323 |
| Fe(B2N3H5)2 | 2.05077 |
| Co(Cp)2 | 2.11688 |
| Co(BC2N2H5)2 | 2.11528 |
| Co(B2N3H5)2 | 2.01201 |
| Ru(Cp)2 | 2.26233 |
| Ru(BC2N2H5)2 | 2.25632 |
| Ru(B2N3H5)2 | 2.18562 |
The reason why the nature of metal complex structures was investigated was that the strength of the interactions between an electrophile and a nucleophile depends on their relative softness and hardness (Co is harder than Mo since it is further on the right of the periodic table; increased electronegativity; Ru is softer than Mo due to its increased atomic/ionic size). However, the trends in the appearance of the metal-complexes was not altered by changing the metal centre used.
 |
   |
The change imposed on the carbonyl groups attached to a metal has also been investigated, since carbonyl groups are π accepting ligands - the extent to which they receive π electrons from the metal d-orbitals (known as back-bonding) depends of the nature of the metal and of the other ligands attached to it. Hence the extent of back bonding and the lewis acidity of the metal influence the degree of nucleophilicity/electrophilicity of the carbon atoms of the carbonyl groups. There are many industrial situations where metal-carbonyl complexes are used, e.g. in hydroformulation (where the carbonyl group is reacted with alkenes to form aldehydes/alcohols). Therefore the reactivity of the carbon atoms of the carbonyl groups, and the ease of their removal is of considerable importance when modifications to these industrial processes are considered (for instance, to enhance the rate of prpopagation of a long-chain organic molecule).
| compound | average C=O length (Å) | average M-CO length (Å) | IR stretches of CO (cm-1) | |
|---|---|---|---|---|
| FeCp(CO)3 | 1.162 | 1.816 | 2059, 2059, 2094 | |
| Fe(BC2N2H5)(CO)3 | 1.152 | 1.870 | 2129, 2133, 2150 | |
| Fe(B2N3H5)(CO)3 | 1.151 | 1.879 | 2135, 2137, 2155 | |
| CoCp(CO)3 | 1.149 | 1.882 | 2156, 2156, 2167 | |
| Co(BC2N2H5)(CO)3 | 1.144 | 1.932 | 2198, 2199, 2202 | |
| Co(B2N3H5)(CO)3 | 1.144 | 1.941 | 2205, 2206, 2208 | |
| RuCp(CO)3 | 1.164 | 1.939 | 2035, 2036, 2088 | |
| Ru(BC2N2H5)(CO)3 | 1.155 | 1.953 | ||
| Ru(B2N3H5)(CO)3 | 1.155 | 1.953 | 2099, 2104, 2143 |
The C=O bonds are shorter when BC2N2H5 or B2N3H5 is attached to the metal centre, and also shows higher wavenumbers on the IR spectra, meaning there is a higher bond order (and so more rigid). The metal-CO distance, however, become longer, implying a smaller bond order - both of these results imply that there is less back bonding from the metal to the carbonyl groups when BC2N2H5 or B2N3H5, rather than cyclopentadienyl anion, is complexed to the metal at the same time. This means that when a partial positive charge builds up on the carbon atom of the carbonyl in nucleophilic addition, there would be less stabilisation by the metal as it would be less eager to carry out back bonding, and so the reactivity of the carbonyl towards nucleophilic attack is reduced. If such analogues of cyclopentadienyl anion can be produced, they could be exploited when a synthesis requires the attachment of a carbonyl group onto the more reactive C=C double bond of a diene. Alternatively a metal with BC2N2H5 or B2N3H5 may be used for syntheses requiring Schrock carbenes, with the ring systems stabilised kinetically.
Job ID of the calculations done on SCAN for this exercise: 10235-10243, 10246-10250, 10314-10331, 10507-10524.
References
1.F. Albert. Cotton, Donald J. Darensbourg, Simonetta. Klein, and Brian W. S. Kolthammer Inorg. Chem., 1982, 21 (1), 294-299 • DOI: 10.1021/ic00131a055
3. Dennis W. Bennett, Tasneem A. Siddiquee, Daniel T. Haworth, Shariff E. Kabir and Farzana Camellia. J. Chem. Cryst., 34 (6) (2004) p353-359
4. Lecture Notes by Dr. Ed Marshall
5. Organometallics - A concise Introduction, Ch. Elschenbroich, A. Salzer, 1989