Rep:Mod:purplevikings

Joseph Downey Year 3 Physical Computational

The Cope Rearrangement

The first part of this experiment centres upon the cope rearrangement of 1,5-hexadiene, a pericyclic [3,3]-sigmatropic rearrangement. This rearrangement can go via two main reaction pathways, the chair or boat transition states. In the following section, the preferred conformations of reactants and products are investigated, the transition structures are optimised and their IRCs and Activation energies are calculated.

1,5-Hexadiene Conformers

HF/3-21G Optimisation

Both the gauche- and anti- conformers of 1,5-hexadiene were modelled in gaussview, cleaned using the inbuilt functionality in the program before Gaussian optimisation at the HF/3-21G level. The energies (Hartrees) were calculated and the molecules were symmetrised and are tabulated below. These results are discussed below.

Conformer	Point Group	Energy/Hartrees HF/3-21G	Energy/kcal/mol	Relative Energy/kcal/mol
Anti	C_i	-231.69253528	-145389.29199717	0.079
Gauche	C₁	-231.69266120	-145389.37101318	0.000

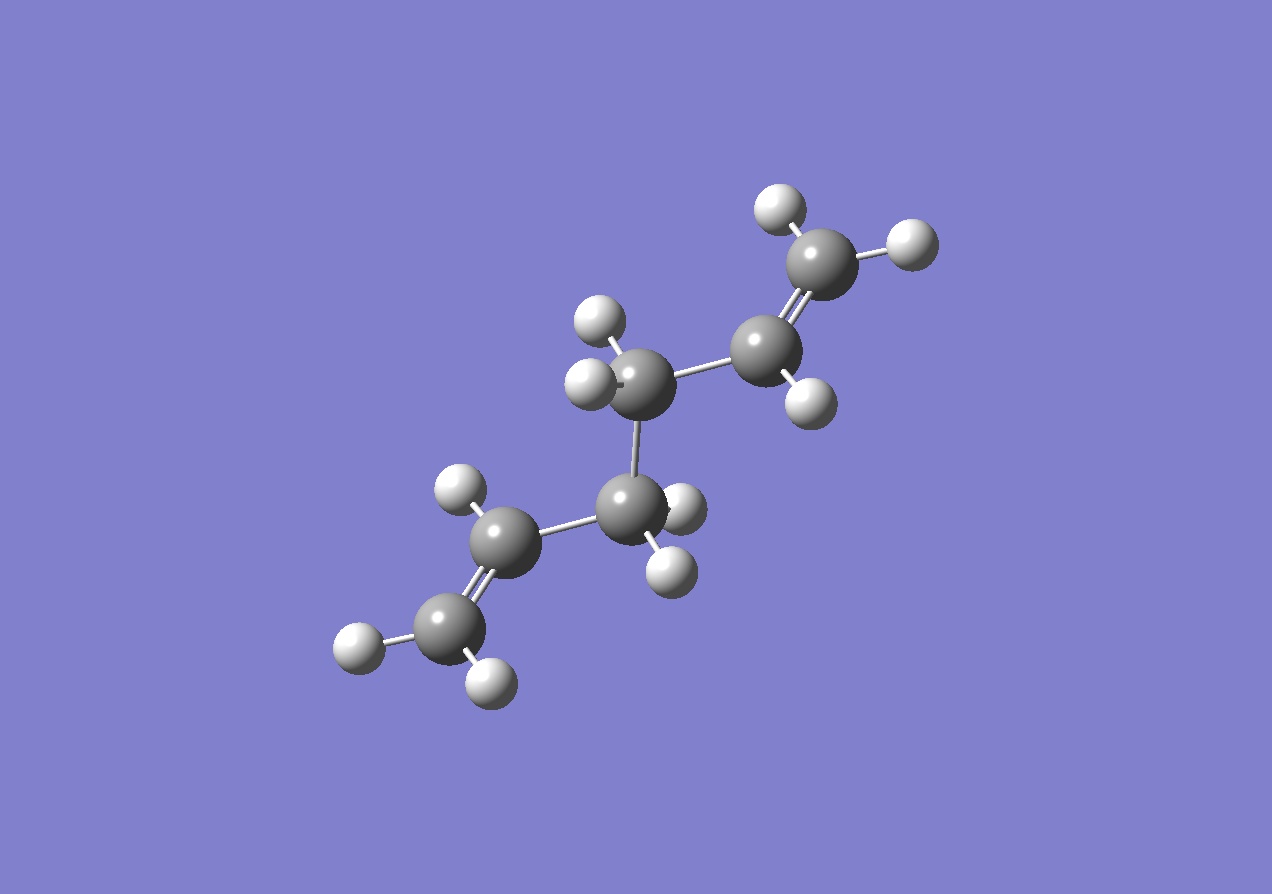
These gauche and anti structures shown here were the first structures generated in gaussview. By comparison to the appendix in the script, these structures were shown to be the lowest energy conformers and so further modelling was not necessary. The important feature to note is that the gauche conformer is marginally lower in energy than the anti conformer. This is potentially due to some energetically favourable van-der-waals dispersion reactions arising as a result of the chain folding back on itself - a trend noticed in alkyl chains of increasing lengths. This energetic favouring of the gauche conformer would be expected to be more noticeable were we, for example, investigating 1,7-octadiene instead.

B3LYP/6-31G(d) DFT Optimisation

The HF/3-21G optimised anti-conformer as obtained in the previous section was reoptimised further at the B3LYP/6-31G(d) DFT level. This is a higher level of optimisation and thus should give a higher degree of accuracy. The energies and point ggroup are tabulated below.

Conformer	Point Group	Energy/Hartrees HF/3-21G	Energy/kcal/mol	Relative Energy/kcal/mol Compared to HF/3-21G values
Anti	C_i	-234.61170280	-147221.09766342	-1831.806

As can be seen above, this level of optimisation led to a significant overall energy decrease. The main way in which this manifests is in a notable change in geometry. This anti-conformer of 1,5-hexadiene consists of two planar propenyl sections bonded together but offset from one another - hence the C_i symmetry. By comparing the 3D Jmol models of the HF/3-21G and the B3LYP/6-31G(d)optimised conformers, it is easy to see how this further optimisation has changed the geometry. The HF optimised structure is closer to overall planarity (109.4 degrees) than the the DFT optimised structure at a higher level of theory (111.349 degrees).

Frequency calculations were then carried out in gaussian and a this theoretical IR spectrum was produced as well as the following thermochemical values being calculated.

Property	Energy/Hartrees
Electronic and zero-point Energies	-234.466691
Electronic and thermal Energies	-234.461098
Electronic and thermal Enthalpies	-234.460154
Electronic and thermal Free Energies	-234.495963

Transition Structures

The chair and boat tranition structure of the cope rearrangement consist of two 'stacked' allyl fragments with differing symmetries. These tow transition states were modelled and optimised (using three distinct methods), the reaction co-ordinate visualised and the activation energies calculated and compared. (All calculations were carried out at the HF/3-21G level)

Optimisation to TS(berny)

In gaussian, two C₃H₅ allyl fragments were positioned in a roughly "chair" arrangement, with a distance of ~2.2 Å between the terminal alkyl groups. This initial guess transition state was optimised to TS(berny) at the HF/3-21G level, and visualisation of the imaginary frequency at -818.79 cm¹ gave the vibration visible in the GIF to the right. This optimisation gave the energy to be -231.61932236 hartrees and the symmetry as C_2h. It can be seen that the terminal protons on each fragment are partially deflected out of the plane away from the other fragment, as would be expected in this reaction. The log file can be found here.

Optimisation by Frozen Co-ordinate Method

Chair Transition Structure Calculated by Frozen Co-ordinate Method

An alternative method for transition structure determination and optimisation is the frozen co-ordinate method. This involves producing a guess structure as before, but fixing the newly formed bond lengths and as such acts to guide a transition structure calculation in a certain direction.

For this tutorial section, the same chair guess structure was used as for the previous method but the inter-terminal-carbon distances were initally fixed at 2.2 Å separation - with the intention that this would guide the calculation towards bond formation between these atoms. The transition state calculated here is very similar to that calculated in the earlier optimisation calculation.

The log file for this calculation can be found here.

Optimisation by QST2 Method

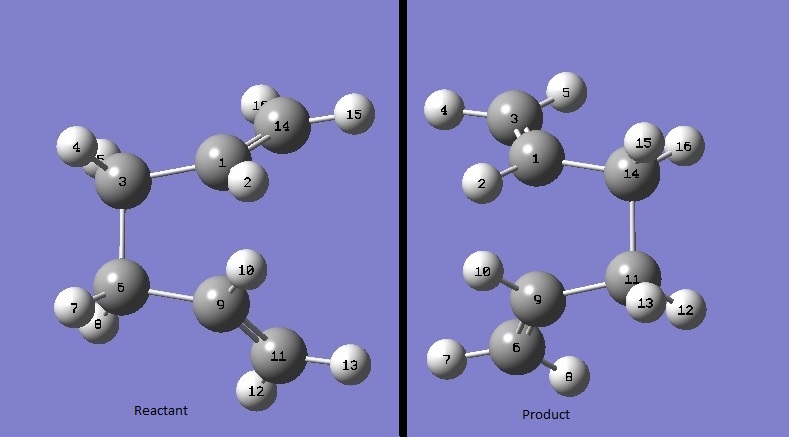
The QST2 method allows you to specify both the products and reactants of a reaction and plot a transition state between the two. This involves modelling both the reactants and the products of the cope rearrangement and choosing to optimise them in gaussian to TS(QST2). This gives a transition structure showing how one turns into the other.

Firstly, this was calculated using the anti conformer of 1,5-hexadiene with the results illustrated to the right. As can be seen, this technique attempts to literally form bonds between the two terminal ends of the molecule, regardless of the fact that their interatomic distance is much too great.

To remedy this situation, this molecule was manipulated into a gauche conformation, bringing the terminal atoms to within a reasonable bond-forming distance (as shown above) and the results of the QST2 calculation are shown to the right. The transition structure is very similar to that calculated in the previous two methods, and shows that the anti form cannot undergo the cope rearrangement without first changing conformation to the gauche form.

IRC Calculation

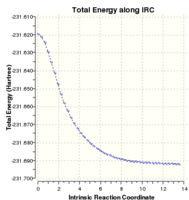
It is possible to follow the path of a reaction via the Intrinsic Reaction Co-ordinate method (IRC), which allows you to visualise the minimum energy pathway along a reaction's potential energy surface, from the transition state to a local minimum. This method involves making small geometrical changes to the transition structure and measuring the potential energy change at each stage. The method continues down the potential energy slope with the steepest gradient since it seeks to minimise the structural energy as fast as possible. This enables a good visualisation of the reaction pathway of a particular reaction, provided that a good transition structure can be correctly guessed and then optimised. A GIF visualisation of this IRC can be seen to the right, as can a graph of the IRC, showing the 44 points calculated along the potential energy surface until a minimum was reached.

IRC helps us to understand what product a transition state will initially lead to, something that is not easily done manually by simple inspection of a transition state.

Activation Energies

The chair and boat transition states, and the C_i anti conformer were all optimised, first at HF/3-21G and then at B3LYP/6-31G(d) levels to allow activation energy calculations. The energies (in hartrees) are tabulated below.

Structure	Electronic and zero-point energies HF/3-21G	Electronic and thermal energies HF/3-21G	Electronic and zero-point energies B3LYP/6-31G(d)	Electronic and thermal energies B3LYP/6-31G(d)
Boat Transition State	-231.450927	-231.445299	-234.402342	-234.396008
Chair Transition State	-231.46669	-231.461339	-234.414929	-234.409009
Anti 1,5-hexadiene	-231.539539	-231.532565	-234.466691	-234.461098

By comparing the energies of the transition states to the energies of the final product (anti 1,5-hexadiene) one can find the activation energies (in kcal/mol).

Structure	HF/3-21G	B3LYP/6-31G(d)	Experimental
ΔE (Boat)	55.60	40.38	44.7 ± 2.0
ΔE (Chair)	45.71	32.48	33.5 ± 0.5

These activation energies are in good agreement with the values in the appendix and literature (in the script), as well as confirming the theory that says that the chair activation energy would be significantly lower than that for the boat.

The Diels-Alder Cycloaddition

The Diels-Alder reaction is a [4s+2s]-cycloaddition that is said to be pericyclic in nature - in that it goes via a concerted transition state whereby bonds are broken and formed simultaneously. Key to understanding this reactivity is investigation of the molecular orbitals involved in this reaction and their symmetries.

To understand this reaction better, both the prototypical reaction and one involving more substituted reactants will be modelled, the transition structures optimised and the frontier molecular orbitals discussed.

The prototypical Diels-Alder is between the electron-rich cis-butadiene and the relatively electron-poor ethylene (a dienophile). To understand the reactivity it is first important to visualise the frontier molecular orbitals of both reactants.

Prototypical Transition Structure

MO Symmetry Calculations

Cis-butadiene and ethylene were both modelled in gaussview before optimisation at the semi-empirical AM1 level. The frontier MOs were visualised and are tabulated below.

Molecule	HOMO	Symmetry	LUMO	Symmetry
Cisbutadiene		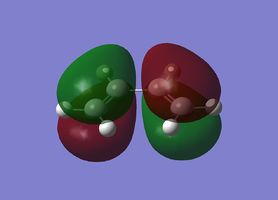Antisymmetric		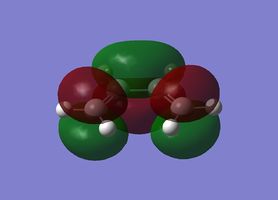Symmetric
Ethylene		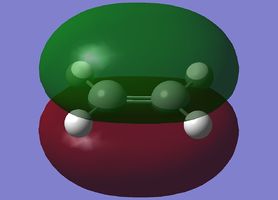Symmetric		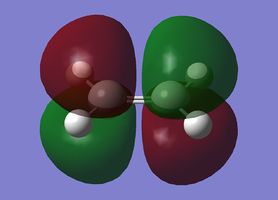Antisymmetric

Transition Structure

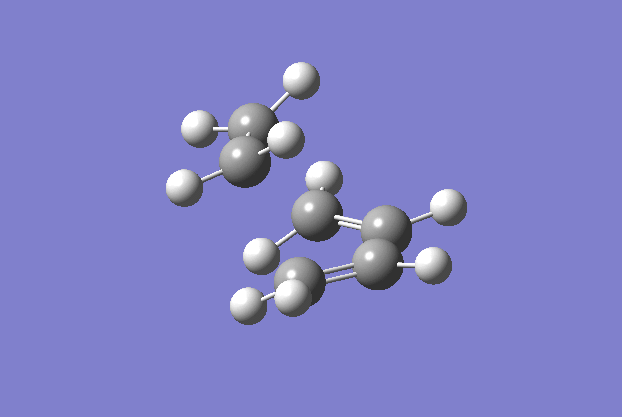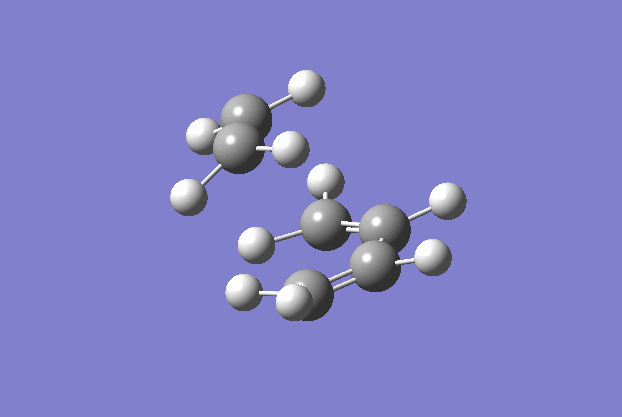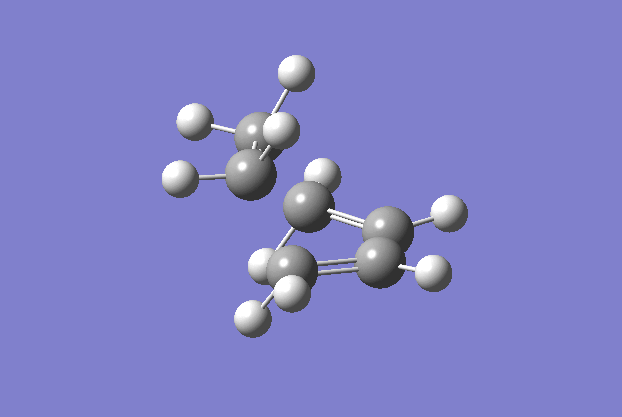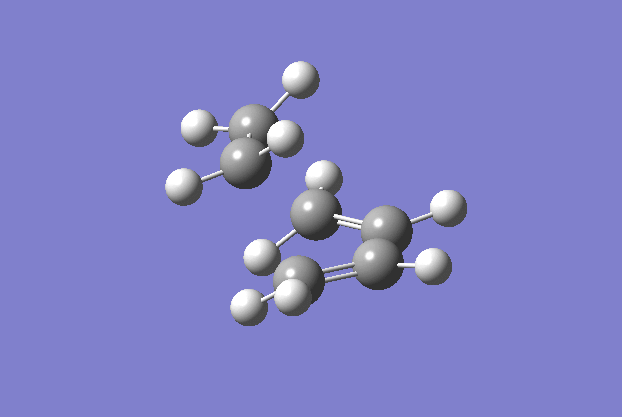
The transition structure was generated using the TS(berny) optimisation method at the semi-empirical AM1 level. To generate a guess structure, the bicyclo[2.2.2]octane structure was generated before removing the bridging group, to leave a structure with the expected geometry of the transition state. This transition state was optimised as detailed above to give the structure as shown to the side. The imaginary frequency noted is also animated in the GIF to the right, and corresponds to the Diels-alder reaction. As can be seen, this is a symmetric vibration and hence tells us that the bonds are formed simultaneously and in a concerted manner, as would be expected from a pericyclic reaction. The bond breaking/forming length here is 2.119 Å.

This reaction takes place between the HOMO of one reactant and the LUMO of the other. For this to be an allowed reaction therefore, the HOMO of one reactant must be of the same symmetry of the LUMO of the other, for this reaction to be quantum mechanically allowed. As is shown in the table above, the LUMO of cis-butadiene is symmetric the HOMO of ethylene is also symmetric, whereas the HOMO of cis-butadiene is antisymmetric and the LUMO of ethylene is antisymmetric. The symmetries of the reactants is correct, and hence this reaction is quantum mechanically allowed and so proceeds via a concerted pericyclic transition state.

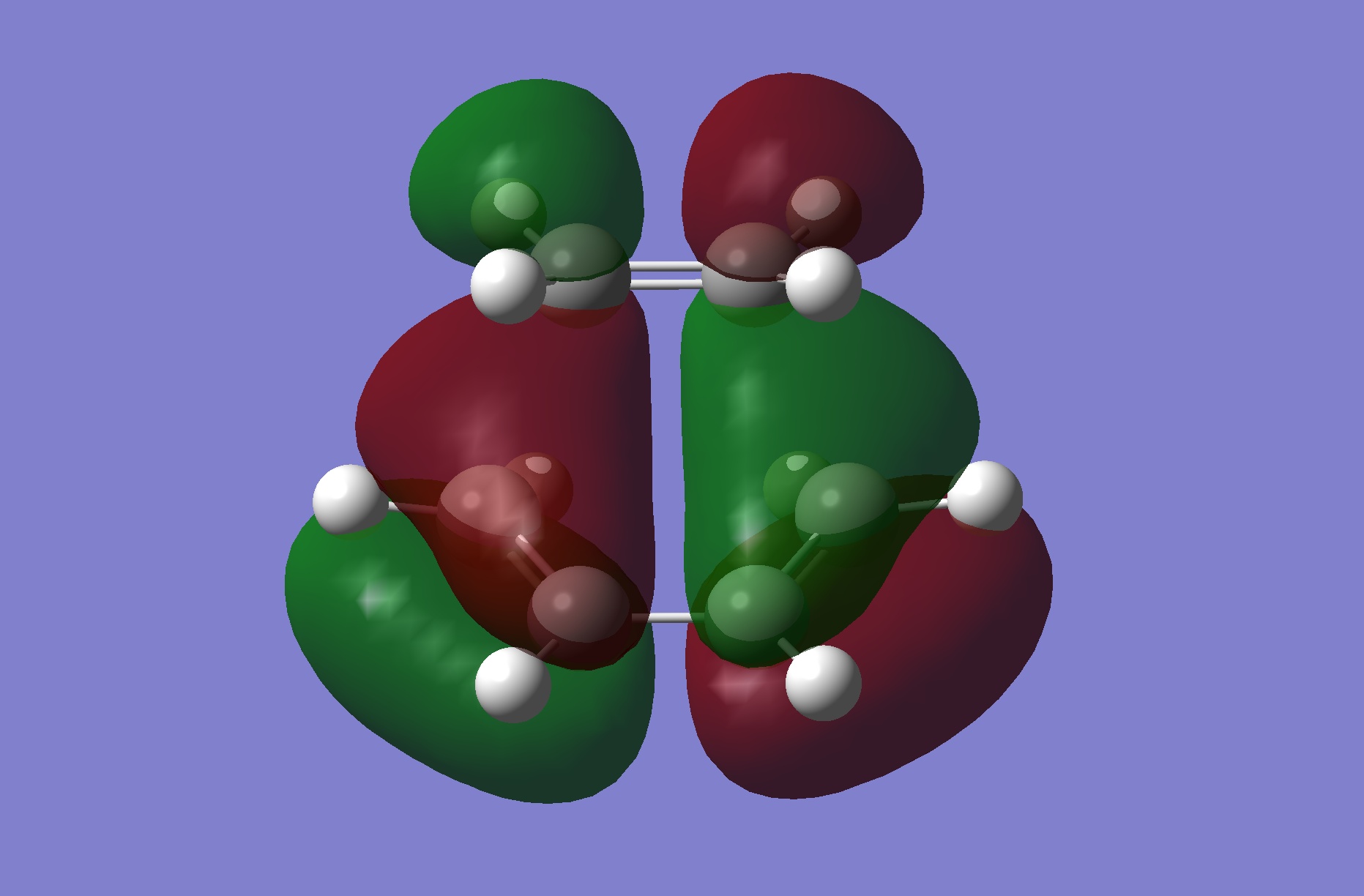
HOMO of Diels-Alder Transition Structure

The HOMO of this transition state is illustrated to the right. It is antisymmetric and hence suggests that it must be the antisymmetric frontier MOs of the reactants that are involved in this MO. These are the HOMO of cis-butadiene and the LUMO of ethylene. Because these are of the same symmetry, this confirms that the reaction is quantum mechanically allowed.

The log file for this transition structure can be found here.

Cyclohexadiene and Maleic Anhydride Transition Structure

MO Symmetry Calculations

Cis-butadiene and ethylene were both modelled in gaussview before optimisation at the semi-empirical AM1 level. The frontier MOs were visualised and are tabulated below.

Molecule	HOMO	Symmetry	LUMO	Symmetry
Cylohexadiene		Antisymmetric		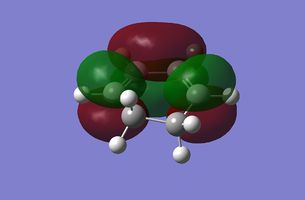Symmetric
Maleic Anhydride		Symmetric		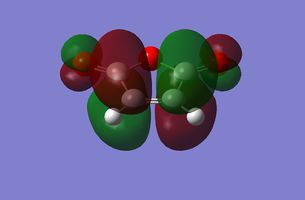Antisymmetric

Transition Structure

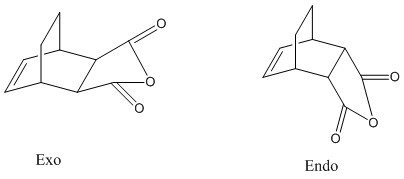
This reaction is a little more complicated than the prototypical reaction due to the fact that both the diene and the dienophile are now substituted. Maleic Anhydride replaces ethylene and cylohexadiene replaces cis-butadiene The major effect that these substituents have is the fact that they open up the possibility of forming either an exo or endo conformer (as illustrated to the right).

Frequencies

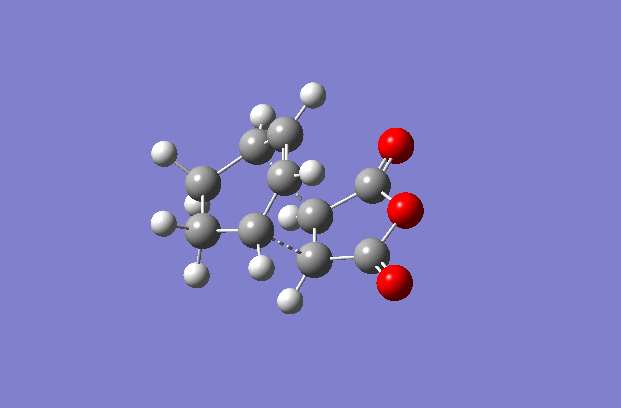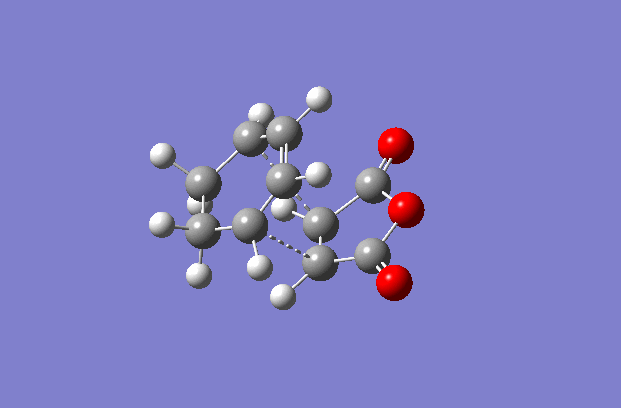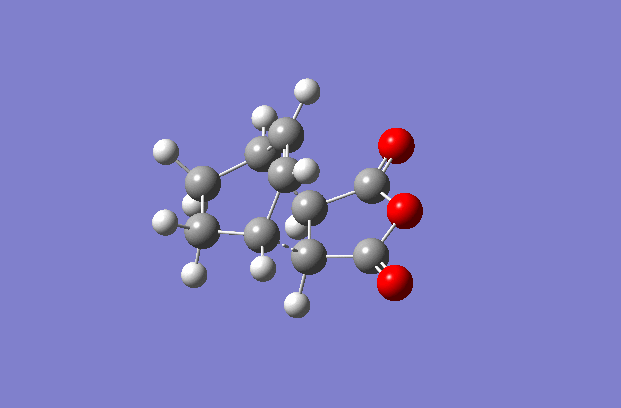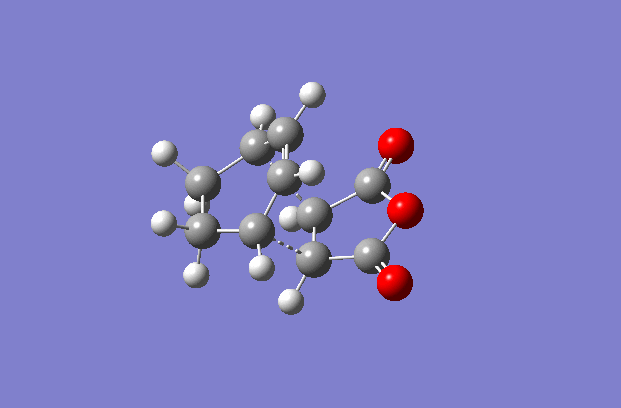
The transition structures were generated using the TS(berny) optimisation method at the semi-empirical AM1 level. To generate a guess structure, the endo and exo structures were generated and the breaking/forming bond was set to 2.2 Å , to leave structures with the expected geometries of the transition state. This transition state was optimised as detailed above to give the structures as shown to the side. The imaginary frequencies noted are also animated in the GIF to the right, and correspond to the Diels-alder reaction. As can be seen, this is a symmetric vibration and hence tells us that the bonds are formed simultaneously and in a concerted manner, as would be expected from a pericyclic reaction. The bond breaking/forming length for exo is 2.16972 Å, and the bond breaking/forming length for endo is 2.16231 Å.

Frontier MOs

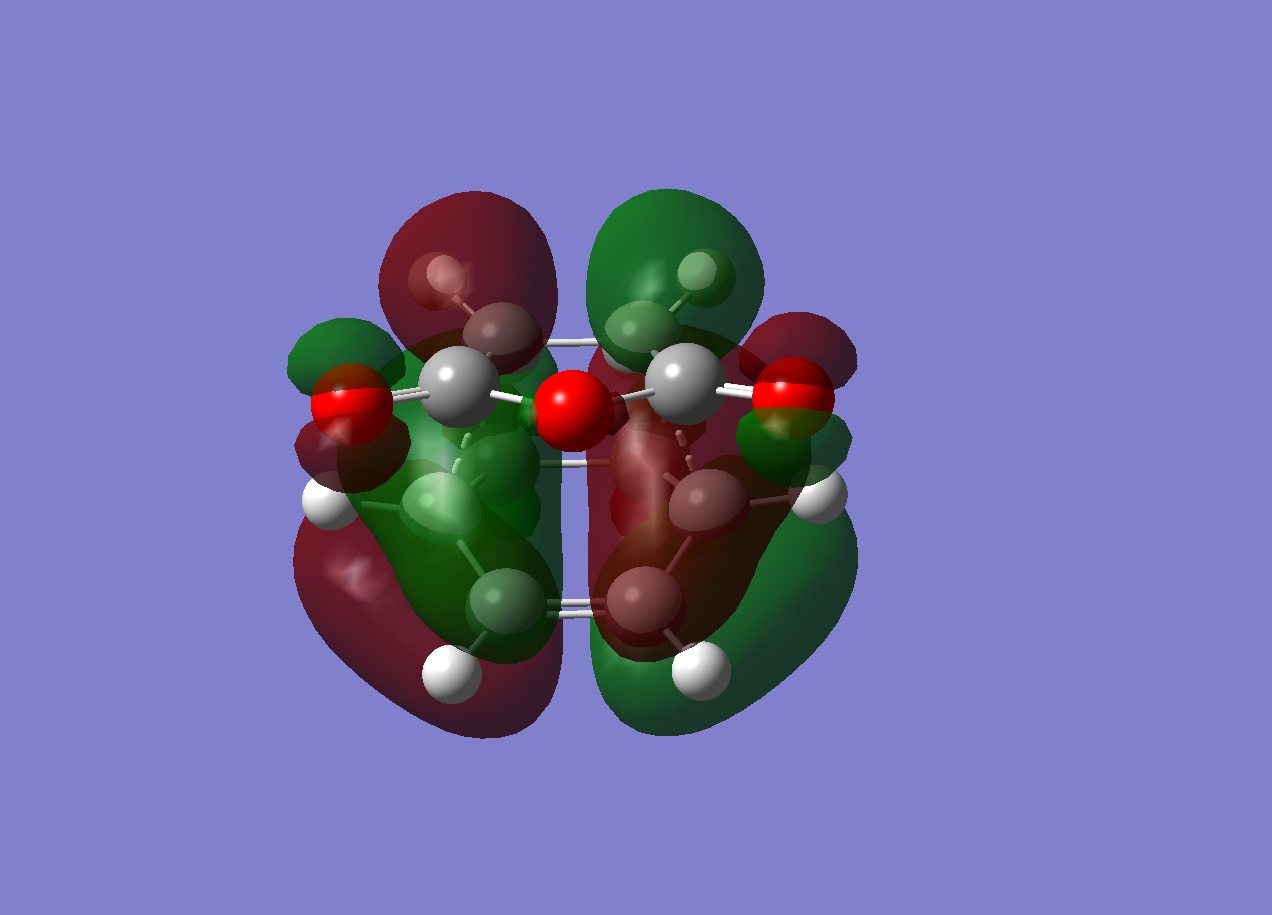
The HOMOs of both transition states are illustrated above. They are comparable to the previous prototypical Diels-Alder transition structure MOs in that it is clear that the HOMOs are antisymmetric, arising from the interaction of the HOMO of cyclohexadiene and the LUMO of maleic anhydride and hence this reaction is quantum mechanically allowed since the interacting orbitals are of the same symmetry

Since the endo form is formed preferentially and the reaction is said to be under kinetic control, this means that we expect the endo transition state to be of a lower energy than for exo, since this is the definition of a reaction under kinetic control. The energy for the endo form is -0.05150479 hartrees, the energy for the exo form is -0.05041966 hartrees. Thus the endo transition state is 0.68093 kcal/mol lower in energy than the exo, explaining why endo is preferentially formed under kinetic conditions.

One possible reason for exo being at a higher energy than endo is due to its steric strain. The -(C=O)-O-(C=O)- section is closer to the sp3 carbons than the sp2 carbons and is thus repelled by the protons on this bridgehead. This can be seen in the node illustrated in the HOMO below. There is very little electron density between this -(C=O)-O-(C=O)- section and the carbons of the bridgehead. By comparison, the endo form is less strained due to its proximity to the sp2 carbons of the bridgehead, not the sp3 carbons. There is visibly more electron density between this -(C=O)-O-(C=O)- and the carbons of the bridgehead due to there not being any protons in close proximity to the -(C=O)-O-(C=O)- section. This nodal difference is well illustrated in the images below.

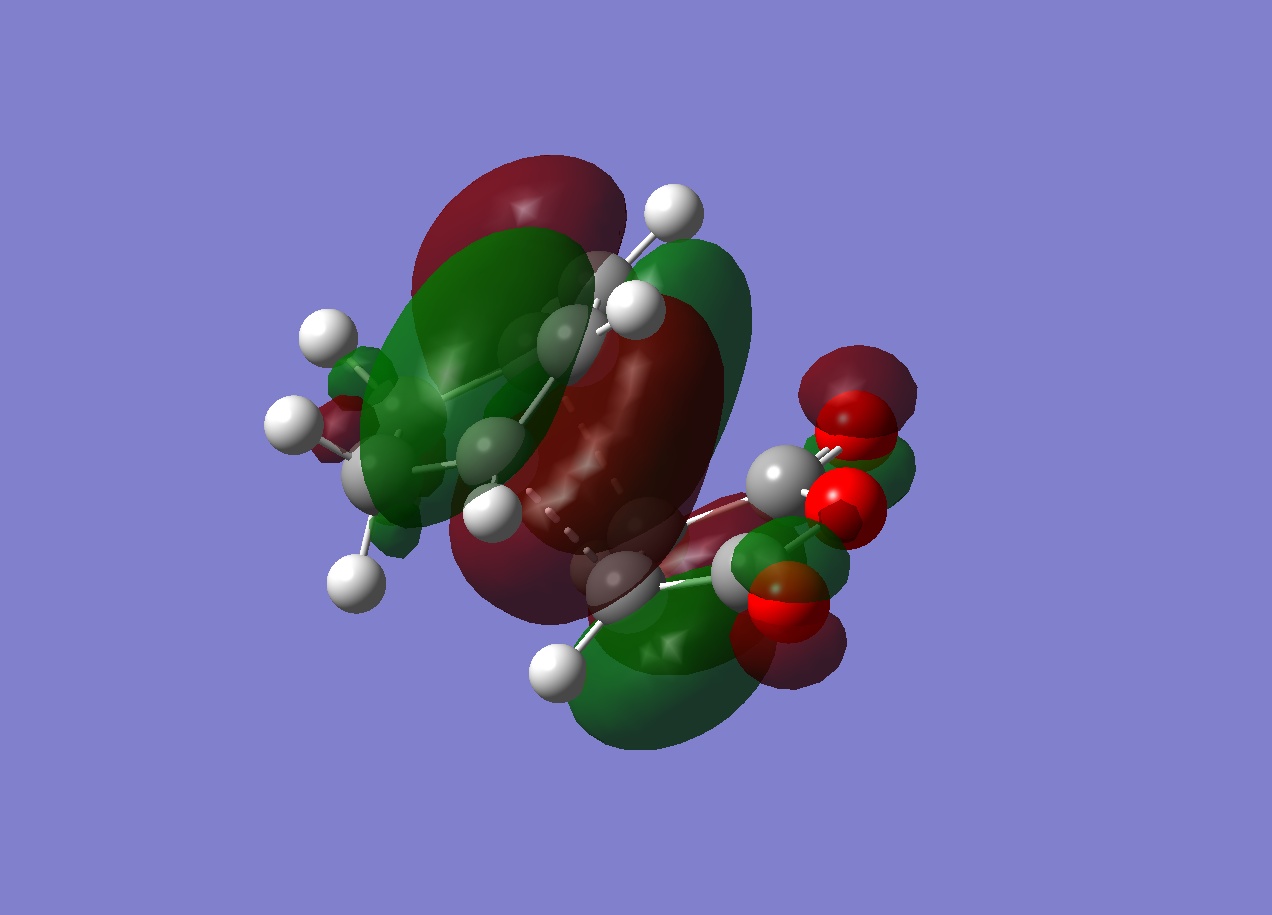
The log file for the endo transition structure can be found here.

The log file for the exo transition structure can be found here.