Rep:Mod:pollybuik

PART 1: The Cope Rearrangement Exercise

In this first part of the exercise, the chemical reactivity problem of the [3,3] sigmatropic shift of 1,5-Hexadiene, known as the Cope rearrangement, was studied to determine the preferred reaction pathway. This was achieved by locating the low-energy minima, ie the conformers of 1,5-hexadiene, and the transition structures on the potential energy surface. All computational operations were carried out using GaussView 5.0. The reaction is said to proceed via either a Chair or a Boat transition states, where the boat transition state is slightly higher in energy, as will be shown at the end of this part.

Optimizing The Reactants and Products

Finding the anti conformer of 1,5-hexadiene

Structure
log. file	OPTI_ANTI1SYMM‎
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.69260235 a.u.
RMS Gradient	0.00001824 a.u.
Dipole Moment	0.2021 Debye
Point Group	C2

A guess structure of 1,5-hexadiene was drawn with an anti-linkage for the four central C atoms by setting the dihedral angle to 180° and optimizing it to a minimum at the HF/3-21G level of theory. The output file gave the total energy of -231.69260235 a.u., that confirmed the structure to be the anti1 conformer of the molecule. Symmetrizing the molecule resulted in a C₂ Point group. The output file proved that the energy minimum had been found, showing the energy convergence of the conformer. This information, extracted from the output file, is presented below.

Item Value Threshold Converged? Maximum Force 0.000056 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000379 0.001800 YES RMS Displacement 0.000158 0.001200 YES Predicted change in Energy=-1.534556D-08 Optimization completed. -- Stationary point found.

Finding the gauche conformer of 1,5-hexadiene

Structure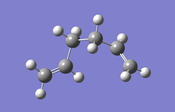
log. file	OPTI_GAUCHE3_SYMM‎
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.69266120 a.u.
RMS Gradient	0.00001175 a.u.
Dipole Moment	0.3405 Debye
Point Group	C1

Next, the gauche guess structure was built by setting the dihedral angle to 60° and optimizing the structure to a minimum using Hartree Fock optimization method and the basis set 3-21G. The resulting structure of this calculation had the energy of -231.6926612 a.u., confirming that the gauche3 conformer had been located. Again, checking for the energy convergence in the output file showed that the energy minimum for this conformation had been located. The results of the calculation presented as before.

Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000895 0.001800 YES RMS Displacement 0.000264 0.001200 YES Predicted change in Energy=-3.046774D-08 Optimization completed. -- Stationary point found.

In a butane molecule, for example, the lowest energy conformation is known to be the one with anti-periplanar arrangement of the terminal methyl groups relative to each other, in other words the dihedral angle of 180°. The gauche conformation for butane lies slightly higher in energy. This is mainly due to the effect of σC-H/σ*C-H and σC-C/σ*C-C orbital interactions, which the anti conformer has more of, compared to gauche. In this example of 1,5-hexadiene, however the energies of the two conformers obtained are remarkably similar (anti: -231.6926024 a.u.; gauche3: -231.6926612 a.u.) to 3 decimal places, only 0.04 kcal/mol difference in energy. This outcome suggests that a different theory approach should be used when considering 1,5-hexadiene conformers and that the results should not be expected to correlate with the energies of butane conformers. The lietrature suggests that the difference in behaviour of the conformers of the two molecules arises from an interaction between the π electrons of the C-C double bond and the nearby vinyl proton, known as the CH-π interaction.

10 conformers of 1,5-hexadiene

There are three carbon bonds that can freely rotate in space in 1,5-hexadiene, which allows for total of 27 conformations, only 10 of which are energetically distinct. All these conformers have been located by drawing close guess structures and optimizing them at HF/3-21G level of theory to allow for comparison between the conformers.

Setting the dihedral angle to 180°

Conformer	Structure	Point Group	Energy (au)	Relative Energy (kcal/mol)	Dihedral angle
Anti1 [log]		C2	-231.6926024	0.04	176.9°
Anti2 [log]		Ci	-231.6925353	0.08	180.0°
Anti3 [log]		C2H	-231.6890707	2.25	180.0°
Anti4 [log]		C1	-231.6909706	1.06	178.4°

Setting the dihedral angle to 60°

Conformer	Structure	Point Group	Energy (au)	Relative Energy (kcal/mol)	Dihedral angle
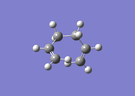
Gauche1 [log]		C2	-231.6877162	3.10	75.8°
Gauche2 [log]		C2	-231.691667	0.62	64.2°
Gauche3 [log]		C1	-231.6926612	0	67.7°
Gauche4 [log]		C2	-231.6915303	0.71	63.6°
Gauche5 [log]		C1	-231.6896157	1.91	71.1°
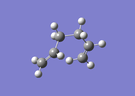
Gauche6 [log]		C1	-231.6891602	2.20	70.2°

All of the checkpoint files of the above structures have been checked for energy convergence to show that the calculation job had gone to completion. The relative energies were converted using the following unit relationship: 1 hartree = 627.503 kJ/mol. The summary of the conformations shows that the energy minimum belongs to the gauche3 conformer, unlike the prediction could have been drawn from the analogy with the butane molecule. However, there is noticeable correlation between the type of the structures (gauche/anti) and their energies. The slightly raised energies are observed in the structures gauche, gauche5 and gauche6, where there is obvious proximity between the protons of two vinyl groups, supposably resulting in a steric clash.

Optimizing anti2 at a higher level of theory

Structure
log. file	OPTI_ANTI2_DFT
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Final Energy	-234.61170280 a.u.
RMS Gradient	0.00001326 a.u.
Dipole Moment	0.0000 Debye
Point Group	Ci

These calculations from the previous section, using the lowest basis set, are quick to carry out but are the least accurate. Thus a more sophisticated optimization of anti2 was carried out using the DFT method and a B3LYP/6-31G* level of theory.

Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000219 0.001800 YES RMS Displacement 0.000079 0.001200 YES Predicted change in Energy=-1.588673D-08 Optimization completed. -- Stationary point found.

The structures optimized at two different methods of theory appear to have the same symmetry, point group remains C_i. The energies, bond distances and angles appear to have some slight differences between two methods of calculating low-energy minima. These differences are summarised in the table below:

	anti2	Dihedral angle	C1-C2-C3 angle	C2-C3-C4 angle	C1-C2 (Å)	C2-C3 (Å)	Total Energy (a.u.)	Point Group
	HF/3-21G	180.0°	124.8°	111.3°	1.316	1.508	-231.6925353	Ci
	B3LYP/6-31G*	180.0°	125.3°	112.7°	1.334	1.504	-234.6117028	Ci

Frequency analysis of anti2

Structure
log. file	OPTI_ANTI2_DFT_FREQ
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d)
Final Energy	-234.61170280 a.u.
RMS Gradient	0.00001310 a.u.
Dipole Moment	0.0000 Debye
Point Group	Ci

The results presented in the section above only give the energy values on a bare potential surface of anti2, that doesn't take into account the corrections that would allow for the comparison with the experimental data. In order to get a more realistic picture, a frequency calculation was carried out on the last optimized anti2 structure at the same level of theory. The output file had no imaginary frequencies, all vibrational frequencies were real and positive, proving that the optimization had found the energy minimum. The results presented below include data from the section Thermochemistry for the energy corrections. A note was taken of the:

• sum of electronic and zero-point energies (potential energy at 0K + zero-point vibrational energy)
  • sum of electronic and thermal energies (potential energy at 298.15K and 1atm: E = E + E_vib + E_rot + E_trans)
    • sum of electronic and thermal enthalpies (includes additional correction for RT)
      • sum of electronic and thermal free energies (includes entropic contribution to the free enrgy)

Zero-point correction= 0.142491 (Hartree/Particle) Thermal correction to Energy= 0.142491 Thermal correction to Enthalpy= 0.142492 Thermal correction to Gibbs Free Energy= 0.142492 Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.469211 Sum of electronic and thermal Enthalpies= -234.469210 Sum of electronic and thermal Free Energies= -234.469211

These corrections were recalculated at 0K at the same level of theory by manually editting the input file. Thermochermistry data is presented below.

Zero-point correction= 0.142491 (Hartree/Particle) Thermal correction to Energy= 0.149847 Thermal correction to Enthalpy= 0.150791 Thermal correction to Gibbs Free Energy= 0.110882 Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821

Optimizing the Boat and Chair Transition Structures

In this section the transition structures for the Cope rearrangement were optimized using three different methods: Whole Hessian, Frozen Coordinate method and QST2 method. Finally, the Intrinsic Reaction Coordinate method was used to predict and study the the minimum energy path from a transition structure to its local minimum on a potential energy surface.

Optimizing the allylic fragment

log. file	ALLYL_OPTI_HF321G‎
Calculation Type	FOPT
Calculation Method	UHF
Basis Set	3-21G
Final Energy	-115.82304010 a.u.
RMS Gradient	0.00003049 a.u.
Dipole Moment	0.0292 Debye
Point Group	C2

An allylic fragment was built and optimized at HF/3-21G level of theory. RMS gradient close to zero showed that the optimization located the energy minimum for the given structure.

Item Value Threshold Converged? Maximum Force 0.000048 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000155 0.001800 YES RMS Displacement 0.000070 0.001200 YES Predicted change in Energy=-1.277266D-08 Optimization completed. -- Stationary point found.

This allyl fragment was used to construct a guess transition structure in a chair conformation. Next, two different methods of optimization were used to optimize this guess structure.

Hessian Method

Structure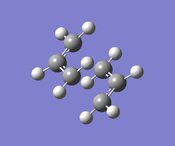
log. file	CHAIRGUESS_HESS‎
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
Final Energy	-231.61932236 a.u.
RMS Gradient	0.00002967 a.u.
Dipole Moment	0.2021 Debye
Point Group	C1

The guess structure was optimized to a transition state TS(Berny) using Opt+Freq and HF/3-21G level of theory, the force constants were calculated once. The outcome file had one imaginary frequency of -817.87cm^-1

Item Value Threshold Converged? Maximum Force 0.000052 0.000450 YES RMS Force 0.000013 0.000300 YES Maximum Displacement 0.000888 0.001800 YES RMS Displacement 0.000246 0.001200 YES Predicted change in Energy=-1.165000D-07 Optimization completed. -- Stationary point found.

The animated transition structure below agrees with the way the Cope rearrangement is expected to proceed.

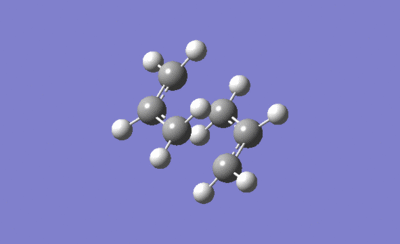
PART2: The Diels Alder Cycloaddition

Optimizing cis-Butadiene

Structure
log. file	CIS_BUTADIENEAM1‎
Calculation Type	FOPT
Calculation Method	RAM1
Basis Set	ZDO
Final Energy	0.4879719 a.u.
RMS Gradient	0.00001745 a.u.
Dipole Moment	0.0414 Debye
Point Group	C2V

A cis structure of butadiene was built in GaussView with a dihedral angle set to 0° and optimized using a AM1 semi-empirical method. The output file was inspected for the convergence of the force and displacement, to ensure the energy minimum had been located for the given structure. Additionally, the RMS gradient is very close to zero, which also provides good evidence for the energy convergence.

Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000407 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-9.691183D-09 Optimization completed. -- Stationary point found.

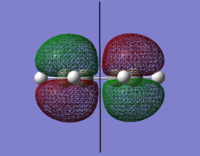
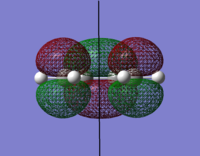
The orbital surfaces were displayed from the checkpoint file and analysed with respect to the horizontal plane.

HOMO	LUMO
Antisymmetric	Symmetric

Optimizing the guess transtition structure for Diels Alder cycloaddition

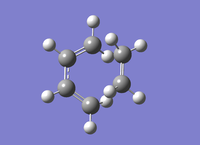
A guess structure of the "envelope" transition state of the cycloaddition reaction between ethylene and the optimized molecule of butadiene was constructed in GaussView, placing the fragments ~2.2Å apart. Three different methods of optimization were used in the following sections to locate the transition states of the reaction. The optimizations are summarised below.

	Hessian	Frozen Coordinate	QST3	Transition state guess
Structure
log. file	TS1_HESS	TS1_FROZ	TS1_QST3
Calculation Type	FREQ	FOPT, then FREQ	FREQ
Calculation Method	RHF	RHF	RHF	TS antimation
Basis Set	3-21G	3-21G	3-21G
Energy (a.u.)	-231.60320853	-231.60320799	-231.60320851
Imaginary Freq (cm-1)	819.35	818.17	818.49
Point Group	C1	C1	C1

Molecular orbitals of the Transition state

The Diels Alder cycloaddition is classified as [_π4_s+_π2_s] since the diene interacts via its 4 π electrons and the dienophile does it via its 2π electron system to form 2 new σ bonds. The intercation between the reactants is such that one fragment reacts via its HOMO and the other via its LUMO. In our case of ethylene and butadiene, there are 2 possible ways for the reaction to proceed:

• HOMO of butadiene + LUMO of ethylene
• LUMO of butadiene + HOMO of ethylene.

The requirement is such that only the molecular orbitals of the same symmetry can interact. HOMO and LUMO of the optimized transition state were visualised with respect to the plane of symmetry and the symmetries were assigned.

HOMO	LUMO
Symmetric	Symmetric

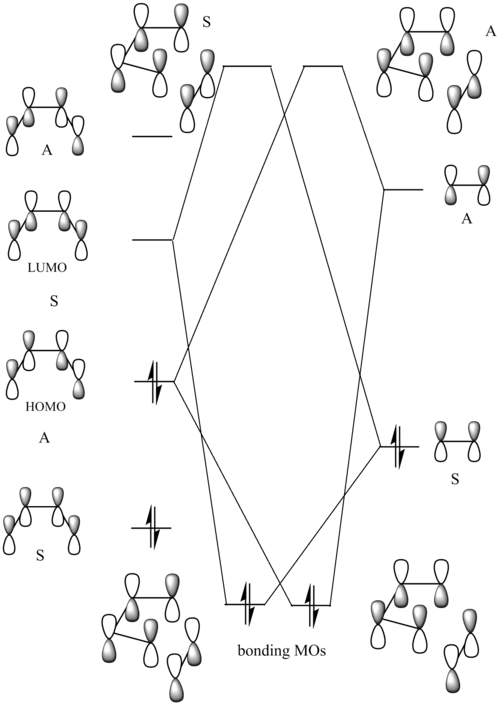
The analysis of these molecular orbitals visualised from the generated transition state shows that this HOMO-LUMO pair is symmetric at the transition state. In fact, there are two types of HOMO-LUMO pairs, as was discussed previously. This schematic MO diagram below shows the possible interactions leading to transition state-like structures:

• symmetric LUMO of butadiene + symmetric HOMO of ethylene
• antisymmetric HOMO of butadiene + antisymmetric LUMO of ethylene

Computational analysis carried out in this section on the transition structure showed that the obtained structure had the symmetric HOMO-LUMO pair, from which we can conclude that the reaction proceeds as follows: s LUMO of butadiene interacts with the s HOMO of ethylene to form two new σ bonds in a concerted fashion, as shown in the animated image of the transition state obtained before. This conclusion agrees with the classification of the given pericyclic reaction as [_s4_π + _s2_π] cycloaddition.

Geometry of the Transition state

Here the transition state that was previously optimized will be analysed in terms of bond lengths and bond orders to provide evidence for the expected reaction pathway.

	C1-C2/C3-C4 (Å)	C5-C6 (Å)	C2-C3 (Å)	C1-C5/C4-C5 (Å)	sp3 C-C (Å)	sp2 (Å)
	1.37	1.38	1.39	2.21	1.53-1.55	1.31-1.34

Comparing the computed bond lengths to the literature values we can see that the double bonds of the butadiene and ethylene are elongated in the TS, which agrees with expectations of those bonds becoming C1-C2 and C3-C4 single bond in the product. Furthermore, the C2-C3 bond is now much shorter than a typical single bond, since it is going to become a double bond in the product. Finally, the distance between the reacting fragments is the same on both sides, that is good evidence for the previosuly stated fact that the cycloaddition occurs in a concerted fashion. This distance is less than the twice the Van der Waal radii of carbon (1.70Åx2), so the fragments are approaching each other to form bonds simultaneously.