Rep:Mod:pnr08mod3
Cope Rearrangement
The Cope Rearrangement of 1,5-hexadiene is the archetypal [3+3]-sigmatropic rearrangement. It is a useful reaction to study as an introduction to modelling transition states, since the reaction is symmetrical (in that the product and reactant are identical), and so is the product (hence reactant) and transition state.
This reaction has been shown to be concerted, hence it can be described as a pericyclic (and a sigmatropic) reaction. This results in a six membered transition state in which the 'shifting' electrons are distributed all the way around the ring. It can be in one of two conformations - a boat or a chair (similar to a cyclohexane ring).
Optimising 1,5-Hexadiene
1,5-Hexadiene, both the reactant and the product of this reaction, has a number of possible conformations, all differing in energy. One easy way to begin to distinguish between them is to separate them into 'gauche' and 'anti' conformations, which refers to the dihedral angle between the two bonds adjacent to (and around) the central bond of the molecule.
First of all, one example of an anti conformation, and one of a gauche conformation were optimised using the Hartree-Fock method of optimisation with the 3-21G basis set. The resulting conformations can be seen by clicking the buttons in the table below. The labelling of the conformation is simply to indicate which of the structures shown in Appendix 1 of the instructional wiki page was created.
| Conformation | Energy / kcal mol-1 | Point Group |
|---|---|---|
| -145389.15 | Ci | |
| -145388.52 | C2 |
The absolute energy seen above is irrelevant; it is simply the relative energy that is important. Here, it can be seen that out of these two, the anti conformation is the most stable, with the gauche conformation being 0.63 kcal mol-1 higher in energy. This could indicate that, as a general rule, anti conformers of 1,5-hexadiene are lower in energy, possibly due to a decrease in steric repulsions. Hence, in an attempt to locate the lowest energy conformation, the anti structure was modified so that the terminal alkene groups point slightly outwards from the effective plane of the molecule, as opposed to being in plane with it, giving the following:
| Conformation | Energy / kcal mol-1 | Point Group |
|---|---|---|
| -145389.19 | C2 |
This structure (anti 1) is marginally (0.04 kcal mol-1) lower in energy than the Anti 2 structure.
However, the energies given here do not show the entire picture. As we will see, the dominant conformation is actually the anti 2 conformer. First of all, 3-21G is low level basis set, therefore the thermodynamic properties calculated using it will not be accurate. To account for this, the anti 2 conformer was reoptimised using the B3LYP method and the 6-31G(d) basis set. It should be noted here that the overall energy given by this was -234.61170393 Ha, equivalent to -147220.96 kcal mol-1. This is lower than the energy calculated before, but since it is calculated using a different method and basis set, they cannot be compared. This will be used to compare with the transition state energies later.
Reoptimising using this higher basis set barely changed the geometry of the structure at all. The only significant difference is that it increased the dihedral angle associated with the four carbon atoms at the end of the chain by about 4o. All other geometric measurements remained more or less exactly the same.
After performing a vibrational analysis on this optimised structure, it can be seen that all of the vibration modes have a positive frequency (i.e. there are no imaginary frequencies), indicating that a minimum energy structure has indeed been reached. Looking in the output file of the vibrational analysis, we can see the following:
| Thermodynamic property | Anti 2 Energy / Ha | Anti 2 Energy / kcal mol-1 | Anti 1 Energy / Ha | Anti 1 Energy / kcal mol-1 |
|---|---|---|---|---|
| Sum of electronic and zero-point Energies | -234.469195 | -147131.53 | -234.469318 | -147131.61 |
| Sum of electronic and thermal Energies | -234.461847 | -147126.92 | -234.461979 | -147.127.00 |
| Sum of electronic and thermal Enthalpies | -234.460903 | -147126.33 | -234.461035 | -147126.41 |
| Sum of electronic and thermal Free Energies | -234.500778 | -147151.35 | -234.500250 | -147151.02 |
The sum of the electronic and zero-point energies is the electronic potential energy plus the zero-point vibrational energy (i.e. the energy at 0K, where there is no translation, rotation or excited vibrational motion). The sum of the electronic and thermal energies adds to this a contribution from vibrational, rotational and translational motion at 298.15K and 1atm pressure (standard conditions). The sum of electronic and thermal enthalpies (again, at standard conditions) is calculated using the equation H = E + RT. Finally, the sum of electronic and thermal free energies is the standard Gibbs Free Energy of the conformation, hence takes into account the entropy (G = H - TS). This is the quantity which determines the proportion of the conformer present (ΔG=-RT ln K).
Comparing this quantity for the anti 1 and anti 2 structures, we can see that even though anti 1 previously was said to have a lower energy, anti 2 has a slightly larger entropy and hence a slightly lower Gibbs Free Energy (by 0.33kcal mol-1, enough to have a significant effect on the equilibrium of conformers). If we were to compare the Gibbs Free Energy of all the conformers, we would find that the lowest, hence the more predominant conformer, is indeed anti 2. Hence, this can be considered our reactant. Note that this only applies under standard conditions, and at any other temperature or pressure, the energies will be different, possibly giving a different dominant conformer.
Optimising the Transition States
Chair

As was mentioned earlier, the transition state for the Cope Rearrangement can have either a chair or a boat-like geometry, in the same way as a cyclohexane ring.
Trying to predict what the transition state will look like, we can note that there are two pairs of sigma bonds (CH2-CH-CH2) unaffected by the reaction, two bonds on opposite sides of the ring that are mid forming/breaking, and six 'moving' electrons, distributed evenly around the ring. This is the same description as could be given two allyl fragment.
Hence, to begin to calculate the transition state, an allyl fragment (CH2-CH-CH2) was optimised using the Hartree-Fock method and 3-21G basis set. This was then replicated and orientated such that the two fragments together formed a chair-like structure, but with two elongated C-C distances (on opposite sides of the ring) of 2.20Å. This structure was optimised to a transition state (a Berny optimisation) using the force constant method (and a vibrational analysis was computed at the same time).
The optimisation changed the structure little, but shifted the allyl fragments relative to each other, so that the elongated C-C bond length was now at an optimal distance of 2.02Å. Looking at the vibrational analysis, it could be seen that there were 42 vibrational modes, as would be expected for a 16-atom molecule. However, one of these had a negative frequency (-817.99cm-1). This is the vibration corresponding to the reaction coordinate, shown to the right, and effectively shows the progress through time of the reaction (one bond forming, one on the opposite side breaking). The fact that there is only one negative frequency indicates that we have indeed reached a transition state.
To both check that this structure was indeed the correct transition state, and simply to practice it, another method of optimisation, the frozen coordinate method was used. In this procedure, the reaction coordinate (i.e. the elongated C-C bonds) are frozen, the rest of the molecule is optimised, then the reaction coordinate is unfrozen and optimised to a transition state.
This method produced almost exactly the same structure. The calculated elongated bond length only differed in the fourth decimal place (it was ever so slightly longer) and the imaginary vibration associated with the reaction coordinate (which appeared exactly the same) was calculated as -817.90cm-1.
Boat

The boat transition state structure was optimised using a different method, the QST2 method. This involved entering the optimised structures of the reactants and products. Obviously, these are the same molecule, however, they were both entered in the lowest energy (anti 2) conformation, and the atom numbers were specified, so that they could be tracked throughout the reaction (for example, the terminal carbon atoms in the reactant become the central carbon atoms in the product and vice versa).
However, optimising this did not work, as this lowest energy conformation was too far away from the transition state. To help solve this problem, the middle dihedral angle was set to 0o and the inside C-C-C bond angles were set to 100o, and the transition state optimisation was attempted again. This time, the optimisation converged to the correct boat structure. The elongated C-C bond length was calculated to be 2.14Å, slightly longer than in the chair structure. This could be indicative of the fact that the boat structure is less stable than the chair, as we will see later.
The same vibration (bond breaking/forming) was found to be the negative frequency in the vibrational analysis, this time at -840.28cm-1. This was the only negative frequency, indicating that the transition state has been correctly located.
Reactive Conformation
From simply looking at the transition state, it is difficult to see which conformation actually reacts (and due to the symmetry of the reaction, is produced), as it does not necessarily have to be (and in fact, is not) the lowest energy conformation. To find this out, and Intrinsic Reaction Coordinate (IRC) calculation was run. This alters the geometry of the structure in small steps according in the direction which the potential energy surface is steepest (which will typically be the reaction coordinate).
This was initially run calculating the force constant once, with a maximum of 50 steps. However, when looking at the convergence graphs, we can see that this is not enough, despite taking a large amount of computing time. After 50 steps, where the calculation was terminated, the energy of the structure was still decreasing, and the gradient of the potential energy surface had not decreased below the threshold value of 0.001 Ha rB-1.
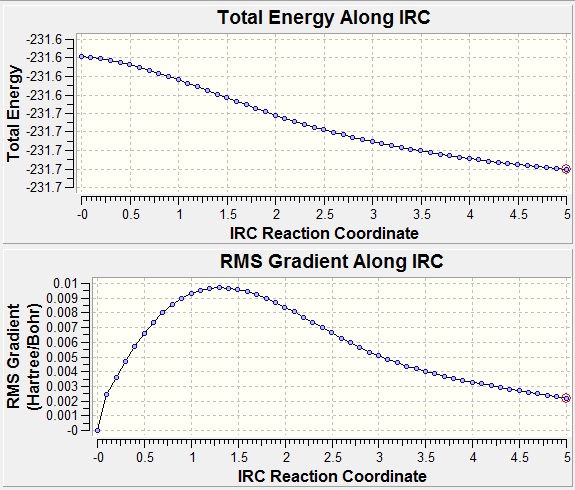
There are a number of different ways that the correct conformer can be calculated from here. The first is to simply run the calculation again with a higher maximum number of steps. Another is to perform a simple geometry optimisation on the output from the initial calculation (as this should be close enough to the correct structure that it will not fall into a different conformers potential well). A third method involves calculating the force constants at every step of the calculation. All three of these methods were attempted, and they all produced the same structure (with a small discrepancy between each method, but not enough to make the absolute configuration ambiguous), which can be viewed here:
This conformation has an energy of -231.69167 Ha (bearing in mind this was calculated using the Hartree-Fock method with the 3-21G basis set) which, when comparing with the table in Appendix 2 of the instructions, can be seen to be the 'Gauche 2' conformation. As a result, we can say that it is likely that the molecules would have to be of a high enough energy to achieve this conformation before they can react.
Activation Energy
However, even these can only react if they have enough energy to reach the transition state. To find these out, the optimised structures of the boat and chair transition states were reoptimised using the B3LYP method and 6-31G(g) basis set. This is the same level of theory that the anti 2 conformation was optimised at earlier, hence the energies can be compared, and the activation energy for the relevant reaction pathway can be calculated by taking the difference of the anti 2 conformation energy and that of the transition state.
| Transition State Structure | Gibbs Free Energy / Ha | Gibbs Free Energy / kcal mol-1 | Activation Energy / kcal mol-1 |
|---|---|---|---|
| Chair | -234.443814 | -147115.60 | 35.75 |
| Boat | -234.431094 | -147107.62 | 43.73 |
Looking at the above results, we can indeed see that the chair transition state is significantly more stable than the boat one, and subsequently the reaction pathway resulting in a chair transition state has a significantly lower activation energy, and will hence react faster. In this particular example, this is of little consequence. However, when the 1,5-hexadiene bears substituents, the different transition states may lead to differing products, in which case, the one obtained through the chair transition state will be the kinetic product.
Diels-Alder Cycloaddition
The Reaction of 1,3-Butadiene and Ethene
The Diels Alder reaction is a [4+2] cycloaddition reaction, and is a pericyclic reaction very similar to the Cope Rearrangement (it can be thought of as its bimolecular counterpart). The simplest reaction of this type occurs between 1,3-butadiene and ethene, as shown below.
To gain an insight into the properties of this reaction, we must first look at the molecular orbitals of the reaction in a little more depth. 1,3-butadiene was optimised using the AM1 semi-empirical molecular orbital method. The resulting HOMO and LUMO can be seen below.
| Orbital | Visualisation | Symmetry w.r.t. reflection plane |
|---|---|---|
| HOMO | 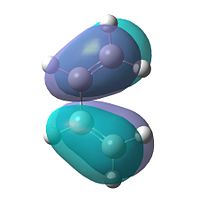 |
Antisymmetric |
| LUMO | 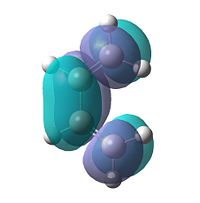 |
Symmetric |
The transition state for this reaction was guess by taking the molecule bicyclo[2.2.2]octane, changing two adjacent methylene groups to hydrogen atom atoms, removing the bond between them, then altering the bond orders and hydrogen counts appropriately. A Berny optimisation was then performed on the structure to obtain a transition state, again using the AM1 semi-empirical molecular orbital method. The resulting transition state structure can be seen here: . Again, there was only one negative frequency vibration, at -955.65cm-1, showing the movement along the reaction coordinate.
The C-C distance in the newly forming bonds is found to be 2.12Å. This is significantly longer than both a typical C-C single bond (1.47Å) and a typical C=C double bond (1.35Å), therefore the partly formed bond has a bond order significantly less than 1. The other C-C bonds in the molecule are between 1.38-1.39Å, indicating that they have a bond order between 1 and 2. This is to be expected since they are all either double bonds losing electron density to form single bonds, or single bonds gaining electron density to form double bonds.
The HOMO of the optimised transition state structure is shown below. Looking at this, we can see that it is antisymmetric with respect to the reflection plane (which is in the plane of the screen). It is formed by the bonding combination of the HOMO of 1,3-butadiene (also antisymmetric) and the LUMO of ethene (which is a π* orbital, also antisymmetric). Note that only orbitals of the same symmetry can combine to form a new orbital, as this is the only way they can have a significant overlap.
Similarly, the LUMO is also shown, which is symmetric with respect to the reflection plane. This is made up of the LUMO of 1,3-butadiene and the HOMO (π orbital) of ethene, both of which are also symmetric. As a result, whichever way round you look at it, the HOMO of one of the reactants can interact strongly with the LUMO of the other, fulfilling the criteria for an allowed reaction. Because of this, the reaction is truly pericyclic, with both bonds forming in a concerted fashion, as shown here.
| Orbital | Visualisation | Symmetry w.r.t. reflection plane |
|---|---|---|
| HOMO |  |
Antisymmetric |
| LUMO |  |
Symmetric |
The Reaction of Cyclohexa-1,3-diene and Maleic Anhydride
The reaction between cyclohexa-1,3-diene and maleic anhydride is again a [4=2] cycloaddition. In actual fact, it is precisely the same reaction as before - there are simply substituents involved.

One consequence of there being substituents on the dieneophile is that depending upon the orientation of its approach, there are two different products that can be formed - the exo and endo products as shown above. The transition states corresponding to these two different products were located using the Berny optimisation in a similar way to the reaction above. The initial optimisation was done using the AM1 semi-empirical molecular orbital method, and then a reoptimisation was performed using the Hartree-fock method and the 3-21G basis set. The structures and energies of these can be seen below.
| Structure | Energy / Ha | Energy / kcal mol-1 |
|---|---|---|
| -605.60359117 | -380021.70 | |
| -605.61036823 | -380025.96 |
Here we can see that that the endo transition state structure is calculated to be 4.26 kcal mol-1 lower in energy than the exo transition state structure. The reaction forming the endo product will, as a result, be significantly faster, leading to the predominant formation of the endo structure as a kinetic product. To fully understand this stabilisation, we must look at the HOMOs of both transition states, shown below.
| Exo HOMO | Endo HOMO |
|---|---|
 |
 |
The important orbital overlap with regards to bond formation is the overlap between the HOMO on the outside carbons on the diene and the LUMO on the alkene part of the dienophile, as before. This is present in both the exo, and the endo case. The typical reasoning given for the additional stabilisation of the endo case is an additional overlap between the carbonyl LUMO (π*) orbital, centred on the carbon atoms of the carbonyl groups, and the HOMO on the central carbons on the diene. Due to the relative orientations of the fragments, this overlap is possible in the endo structure, but not the exo one, due to the proximity of the relevant atoms.
However, in the diagrams above, this effect cannot be seen, nor can it be found in any of the immediately energetically surrounding orbitals. This may be down to a variety of reasons. One potential reason is that the basis set and method used here is not sophisticated enough to show this effect. Alternatively, it is possible that this effect is not the dominant effect, and in fact, the destabilisation caused by the steric clash between the anhydride group and the downwards pointing C-H bonds in the two methylene groups in the exo transition state is. This steric clash is present in the exo transition state, causing the slightly longer C-C distance in the forming bond, seen earlier, but not the endo one. This causes the exo structure to be destabilised relative to the endo one, allowing the endo product to become the kinetic product.
