Rep:Mod:pnr08mod1
Modelling Using Molecular Mechanics
Hydrogenation of a Cyclopentadiene Dimer
 |
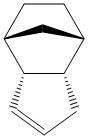 |
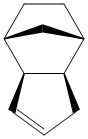
Cyclopentadiene is a synthetically very important molecule, amongst other things, being the protonated precursor to the cylopentadienyl ligand, forming the basis of a huge variety of organometallic complexes. However, in its pure state, it reversibly dimerises in a Diels Alder reaction. As with most Diels-Alder reactions, this can lead to two isomeric products - an endo and an exo form, shown to the right. To obtain the simple monomer, the dimer must be 'cracked' by heating.
| Energy Type | Exo Product Energy / kcal mol-1 | Endo Product Energy / kcal mol-1 |
|---|---|---|
| Stretch | 1.2861 | 1.2443 |
| Bend | 20.6031 | 20.8650 |
| Stretch-Bend | -0.8418 | -0.8283 |
| Torsion | 7.6545 | 9.5047 |
| Non 1,4 VDW | -1.4326 | -1.5320 |
| 1,4 VDW | 4.2351 | 4.3031 |
| Dipole/Dipole | 0.3773 | 0.4461 |
| Total | 31.8817 | 34.0029 |
After optimising the structures in ChemBio3D using the MM2 force field, it is found that the endo product has an energy 2.1212 kcal mol-1 higher than the exo product, predominantly due to a higher torsional strain. However, the endo product is, in fact, the major product of the reaction, despite its relative thermodynamic instability. As a result, it can be deduced that the dimer forms under kinetic conditions. This is as expected; since the dimer is formed in a Diels-Alder ([4+2]-cycloaddition) reaction, it is pericyclic and hence largely controlled by the stability of the transition state, according to the Woodward Hoffman rules.
 |
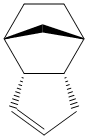 |
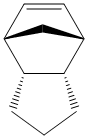
When this endo product is hydrogenated, except under very forcing conditions, only one of the double bonds is hydrogenated. Assuming that the pure endo dimer is being reacted and that tetrahydrogenation does not occur, this gives two possible products, compared below.
| Energy Type | Exo Product Energy / kcal mol-1 | Endo Product Energy / kcal mol-1 |
|---|---|---|
| Stretch | 1.2659 | 1.1030 |
| Bend | 19.8063 | 14.5321 |
| Stretch-Bend | -0.8276 | -0.5502 |
| Torsion | 10.8698 | 12.5087 |
| Non 1,4 VDW | -1.2207 | -1.0642 |
| 1,4 VDW | 5.6394 | 4.4998 |
| Dipole/Dipole | 0.1621 | 0.1407 |
| Total | 35.6953 | 31.1699 |
From these figures, it is quite clear that hydrogenating the double bond in the bridged ring system gives a product that is 4.5254 kcal mol-1 more stable than the product from hydrogenating the cylopentene double bond. As a result, from purely thermodynamic considerations, it can be expected that this is the product that is formed. However, under kinetic conditions, this may not be the case as the bridge in the ring may hinder the approach of hydrogen to this double bond, leaving the cyclopentene double bond more open, potentially allowing it to be preferentially hydrogenated.
Looking in more detail, more stable product has a lower contribution from the stretching, bending, Van der Waals's and electrostatic contributions, all of which stabilise the molecule with respect to the other product, although it does suffer from greater torsional strain. However, this is only a marginal destabilising factor compared to the sum of all the others, hence it is overall more stable.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ Analogue)
Pyridinium cations are susceptible to nucleophilic attack at the ortho and para positions (primarily para if the cation is N-substituted). If the ring is otherwise substituted, then nucleophilic attack can give rise to diastereomeric or enantiomeric products, depending on the precise nature of the substituent.
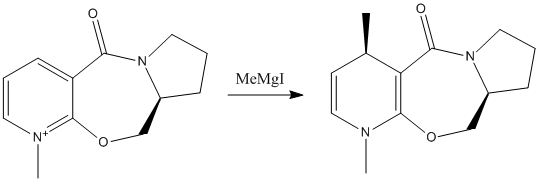 |
Figure 3 - Reaction scheme for the nucleophilic addition to a pyridinium ring
|
In the example below, the substituent contains a chiral carbon atom, meaning that depending on which face of the ring a nucleophile attacks, two different diastereoisomers can be formed. When reacted with Methylmagnesium iodide, only one is predominantly formed.
The 3D structure of the lowest energy conformation of the reagent found can be seen by clicking the button underneath figure 3. The torsion angle between the C=O bond and the pyridine ring is measured at 22.5o, with the carbonyl situated on the same face of the ring that the methyl is found to attack. The rest of the molecule (i.e. the pyrrolidine ring and the rest of the 7-membered ring) is found on the other side of the plane of the pyridinium ring. Therefore, there are two factors that may contribute to the stereoselectivity of the reaction. Firstly, the magnesium could coordinate to the carbonyl oxygen, giving the connected methyl nucleophile a preference to attack from that side of the ring. Secondly, attack from the other side would be subjected to steric hindrance from the rest of the molecule, in contrast to the side attacked, which is totally exposed.
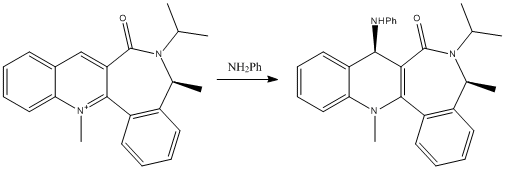 |
Figure 4 - Reaction scheme for the nucleophilic addition to a different pyridinium ring
|
Similarly, this reaction shown proceeds with good stereoselectivity, for the same reasons. Looking at the reagent, we can see that the carbonyl oxygen is on the same face of the pyridinium ring that the methyl adds to (with a torsion angle of 19.1o) and a large part of the molecule is on the other side, providing steric hindrance.
If would be of interest to include the methyl magnesium iodide in the optimisation to prove whether or not this coordination happens. However when attempting this, the Magnesium atom causes an error in the program - 'WARNING! No atom type was assigned to the selected atom!'. The program cannot perform calculations involving the magnesium atom.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Atropisomerism is a form of axial chirality where the rotation about a single bond is hindered as a result of a high steric barrier. As a result, different rotamers can be isolated as separate conformers. One such example is BINAP (2,2'-bis(diphenylphosphino)-1,1'-binaphtyl), a frequently used ligand in asymmetric synthesis. A more subtle example is the molecule shown below, an intermediate compound in the total synthesis of taxol.
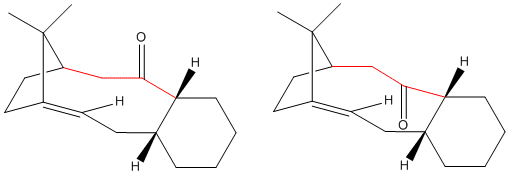
The two atropisomers are primarily characterised by the orientation of the carbonyl group. In one isomer, the carbonyl is pointing up; in the other, it points down. Interchange between the two involves rotation around the 3 bonds highlighted in red in the diagram above. The 3D structures of each can be viewed by clicking the buttons above.
| Energy Type | Point-down Energy / kcal mol-1 | Point-up Energy / kcal mol-1 |
|---|---|---|
| Stretch | 2.5409 | 2.6776 |
| Bend | 10.6059 | 15.8614 |
| Stretch-Bend | 0.3168 | 0.3969 |
| Torsion | 19.7334 | 18.2631 |
| Non 1,4 VDW | -1.2872 | -1.1334 |
| 1,4 VDW | 12.5472 | 12.6759 |
| Dipole/Dipole | -0.1815 | 0.1456 |
| Total | 44.2754 | 48.8872 |
When minimising the energies of the structures using the MM2 force field, it is found that the isomer with the carbonyl pointing down has a significantly lower energy. The contributions from each type of energy are shown to the right. As a result, it can be seen that the atropisomer with the carbonyl pointing down is significantly more stable than the other. When using the MMFF94 force field, the structure changes very little. Obviously, since we are using a different force field, the absolute energy values cannot be compared, but the isomer with the carbonyl pointing down is still calculated to me significantly more stable. Upon standing, the less stable isomer will, given enough time, isomerise to the more stable form.
In fact, this more stable atropisomer is an example of a 'hyperstable alkene[1] ', and reacts at an unusally slow rate. As a general rule, the strain energy is higher in a cycloalkene than in its parent cycloalkane. However, a limited number of compounds present an exception to this rule. Although, in these compounds, the overall energy of the cycloalkene is still higher, specifically the strain energy is lower than in the corresponding cycloalkane (assuming both are in their lowest energy conformations. The compounds that make up these exceptions are termed hyperstable alkenes, and were first discovered in bridgehead alkenes (of which this molecule is an example).
The strain energy associated with a double bond can be investigated using a quantity called the Olefinic Strain (OS), which is related to the enthalpy of hydrogenation in such a way that hyperstable alkenes have a negative OS. This can often be rationalised by the fact that the corresponding cycloalkane will be destablised by vicinal or transannular hydrogen interactions. This can somewhat be seen in the hyperstable alkene's 3D structure, since the hydrogen that is both part of the bicyclic and the cyclohexane ring, which is α to the carbonyl, is significantly bent towards to inside of the room, and as such, is relatively close to the double bond, and would suffer from transannular hydrogen interactions[2] were the double bond to be saturated.
Modelling Using Semi-Empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Simply using molecular mechanics approaches alone cannot account for phenomenon attributed to stereoelectronic effects. One particularly good example is the electrophilic addition of dichlorocarbene to 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonapthalene. This reaction is highly regioselective, with the carbene adding only to the double bond endo (syn) to the C-Cl bond.

Looking purely at steric reasoning, we might expect the chlorine atom over the endo double bond to hinder attack from one face of the molecule more than a hydrogen atom would, and also to potentially create a more destabilised product (since the three chlorine atoms would all be on the same side of the bridgehead carbene, causing steric and electronic repulsion). As a result, the carbene would be expected to react at the exo double bond.
However, as we have seen, this is not the case (though the steric effect of the chlorine does affect the stereochemistry). It turns out that the exo bond is stabilised by stereoelectronic effects, hence the less stable endo double bond reacts.
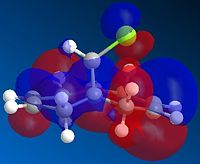
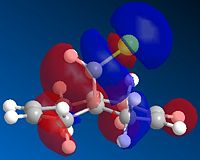
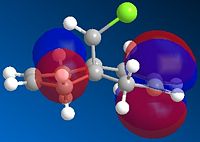
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
|---|---|---|---|---|
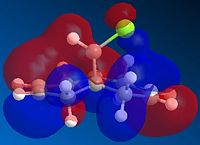 |
 |
 |
 |
|
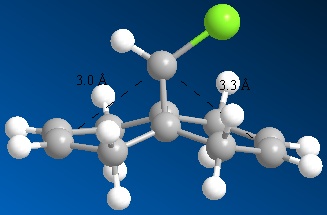 |
Figure 8 - Image showing the differences in alkene-bridgehead distances
|
Above, we can see the frontier orbitals of 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonapthalene. The two most important orbitals are the HOMO-1 and the LUMO+1. The HOMO-1 can be seen to contain a large contribution from the π bonding orbital of the exo C=C bond, whereas the LUMO+1 contains a large contribution from the σ* antibonding orbital of the C-Cl bond. There happens to be quite a large overlap between these two orbitals which results in a stabilisation of this exo alkene bond (hence it is less reactive). This manifests itself in a contraction of the distance between the bridgehead carbon and the exo alkene bond, compared to the endo one. This explains why the MO containing a large contribution from the endo C=C bond (the HOMO) is of a higher energy than the one containing a large contribution from the exo C=C bond (HOMO-1).
In addition to this, the HOMO-1 molecular orbital is more delocalised and contains a significant contribution from the cyclopropyl part of the structure. Since this adds significant electron density to the exo side of the structure, and more than to the endo side (in part due to the orientation of the bridgehead hydrogen, and partly due to the aforementioned contraction), there is a correspondingly lower contribution from the alkene bond itself (else there would be high levels of electrostatic repulsion, destabilising the orbital). This means that there is more electron density available on the endo alkene bond than on the exo one, making it more reactive.
In the molecule resulting from the hydrogenation of the exo alkene bond, the σ* antibonding orbital of the C-Cl bond is found in the LUMO. However, these are no longer any appropriate orbitals for it to interact strongly with.
The degree of interaction can be investigated by computing the frequencies of the vibrational modes associated with the C-Cl and C=C stretches. The table shows these frequencies for both the monoalkene and the dialkene with a variety of substituents on the exo double bond.
| Substituent | Dialkene exo C=C / cm-1 | Dialkene endo C=C / cm-1 | Dialkene C-Cl / cm-1 | Monoalkene endo C=C / cm-1 | Monoalkene C-Cl / cm-1 |
|---|---|---|---|---|---|
| BH2 | 1604.5 | 1758.2 | 761.4 | 1754.3 | 773.7 |
| SiH3 | 1633.8 | 1754.9 | 767.9 | 1758.4 | 778.4 |
| CN | 1670.5 | 1757.1 | 772.6 | 1754.4 | 787.8 |
| H | 1737.1 | 1757.4 | 770.9 | 1753.8 | 779.8 |
| OH | 1798.0 | 1757.7 | 781.1 | 1753.8 | 787.2 |
This provides a useful insight into the effect of these different substituents on the electronic properties of the double bond they are attached to. The more electron donating the substituent, the more electron rich the double bond. This, in turn, causes a greater interaction with the C-Cl σ* antibonding orbital, which will stabilise the double bond by a greater amount. IR Stretches are a good indication of this, as the more stable a bond is, the stronger it is, giving its IR stretch a higher wavenumber (corresponding to a higher energy).
Looking at the table above, we can see that the greatest effect by far is on the exo C=C stretch. From this, we can see that BH2 is the most electron withdrawing of substituents, followed by SiH3, CN, then H, with the most electron donating substituent being OH. BH2 is an electron deficient substituent, hence the fact that it is strongly electron withdrawing is not a surprise. The fact that SiH3 is next on the scale (more electron withdrawing than CN) is perhaps surprising, considering that Si is an electropositive metal. However, it has a large number of empty d orbitals relatively close in energy to the filled C=C π orbital, hence electron density can be donated into those of appropriate symmetry. CN, predictably, is both inductively and mesomerically electron withdrawing, whereas OH is inductively withdrawing, but mesomerically electron donating, hence it is overall electron donating to the C=C bond.
Structural Based Mini Project Using DFT-Based Molecular Orbital Methods
Palladium-Catalyzed [3+2] Intramolecular Cycloaddition of Alk-5-enylidenecyclopropanes
The following reaction[3] is an example of a reaction taking an alkenylidenecyclopropane substrate and, in the presence of a palladium catalyst, ring closes to form a bicyclic compound, consisting of two fused cyclopentane rings.

Apart from the synthetic interest that this reaction presents, even though the substrate contains no chiral centres, the product contains three. As a result, diastereoisomers are formed, as shown in the reaction scheme above (it should be noted that the enantiomers of the above products can also be formed), which can be separated by various forms of chromatography.
One key difference between the diastereomers will be their NMR spectra. 1H, 17O and 13C NMR can all be used to characterise these compunds. The structures of the two diastereomers were optimised and the NMR spectrum predicted using a DFT method (MPW1PW91 to be precise) and the 6-31G(d,p) basis set. The predicted 13C shifts are compared to the shifts quoted in the literature below:
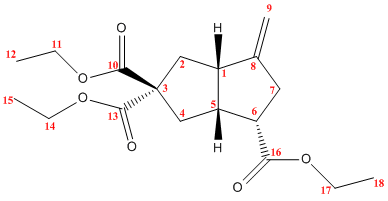 |
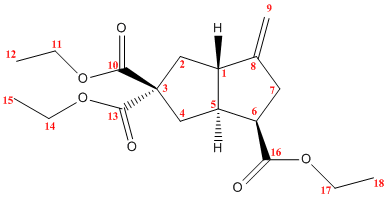 |
| Carbon | Computed Shift / ppm | Literature Shift / ppm |
|---|---|---|
| 1 | 49.7 | 47.5 |
| 2 | 43.9 | 41.0 |
| 3 | 64.9 | 62.0 |
| 4 | 38.8 | 35.8 |
| 5 | 46.8 | 45.4 |
| 6 | 46.4 | 45.1 |
| 7 | 36.3 | 33.1 |
| 8 | 151.9 | 153.4 |
| 9 | 106.6 | 107.5 |
| 10 | 173.2 | 171.1 |
| 11 | 61.8 | 61.4 |
| 12 | 14.8 | 14.3 |
| 13 | 173.6 | 171.8 |
| 14 | 61.8 | 61.4 |
| 15 | 14.7 | 14.0 |
| 16 | 174.7 | 173.2 |
| 17 | 60.9 | 60.4 |
| 18 | 14.8 | 14.3 |
| Carbon | Computed Shift / ppm | Literature Shift / ppm |
|---|---|---|
| 1 | 54.1 | 53.4 |
| 2 | 34.7 | 32.7 |
| 3 | 67.1 | 64.7 |
| 4 | 36.3 | 33.4 |
| 5 | 53.8 | 52.6 |
| 6 | 44.4 | 40.2 |
| 7 | 40.8 | 39.9 |
| 8 | 146.3 | 147.5 |
| 9 | 104.0 | 103.6 |
| 10 | 174.9 | 173.9 |
| 11 | 61.2 | 61.4 |
| 12 | 16.0 | 14.4 |
| 13 | 174.3 | 172.4 |
| 14 | 61.2 | 61.5 |
| 15 | 15.5 | 14.0 |
| 16 | 173.1 | 172.0 |
| 17 | 60.3 | 60.4 |
| 18 | 16.5 | 14.4 |
Comparing the two products, it is quite clear that the authors of the journal article have correctly assigned the diastereoisomers. The largest discrepancy between the calculated and literature values for any of the shifts was 4.2ppm, and the average discrepancy was 1.5ppm. Despite this, there are numerous examples where corresponding carbon atoms in the two diastereoisomers differ by significantly more than this. For example, the shift for the carbon numbered 2 differs by 8.3ppm between diastereomers, significantly larger than the maximum error involved in the computation, and the computed shifts are quite close to the literature values, hence supporting the assignment. Other carbon atoms that show the same are carbon 1 (diastereomers differ by 5.9ppm), carbon 5 (7.2ppm), carbon 6 (4.9ppm), carbon 7 (6.8ppm) and carbon 8 (5.9ppm).
The spectrum for the major product can be found here: DOI:10042/to-6513
The spectrum for the minor product can be found here: DOI:10042/to-6512
The ratio of major to minor product in this reaction is roughly 5.3:1. This can be rationalised by considering the mechanism of the reaction. In the literature, it is proposed that there are two alternative mechanisms by which this reaction could proceed. One of these two mechanisms involves the initial oxidative addition of the active palladium species to the cyclopropane ring, followed by an intramolecular [3+2] cycloaddition, shown below, which subsequently undergoes reductive elimination to give the product.

This cycloaddition step is the stereoselective step of the reaction. Since it is a pericyclic reaction, it is governed by the Woodward-Hoffmann rules. In particular, we have a 6 electron (4n+2 n=1) transition state formed under thermal conditions, hence this must be a Huckel Transition State. Both components of the reaction must hence be suprafacial i.e. it is a π2s + π4s cycloaddition. This limits the products to two diastereoisomer (and their enantiomers) depending on the orientation of one of the double bonds, as shown below.
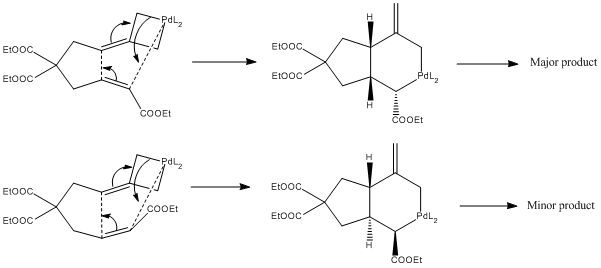
Evidently, due to its steric bulk, the double bond is likely to orientate itself in such a way that the ethyl ester group is pointing away from the rest of the molecule, as this would be lower in energy due to a reduced steric clash. Invoking Hammond's postulate for this exothermic reaction, the transition state will hence have a much lower energy if the ester points outwards. This leads to the observed major diastereomer as the kinetic product of the reaction.
If the DFT optimised structures from the NMR calculation are opened in ChemBio3D, the MM2 energies can be calculated and compared. These are shown below.
| Energy Type | Minor Product Energy / kcal mol-1 | Major Product Energy / kcal mol-1 |
|---|---|---|
| Stretch | 8.5381 | 7.2927 |
| Bend | 22.5876 | 14.5259 |
| Stretch-Bend | 0.2808 | -0.0499 |
| Torsion | 8.3639 | 9.9739 |
| Non 1,4 VDW | -3.0256 | -4.7732 |
| 1,4 VDW | 21.2258 | 20.6727 |
| Dipole/Dipole | 11.0230 | 11.0190 |
| Total | 68.9935 | 58.6612 |
Here it can be seen that the major product is the thermodynamic as well as the kinetic product of the reaction (since the minor product is significantly destabilised by a distortion in its bond angles). Since there is no reason to think that the reaction is irreversible, if it is in fact reversible, then the product mixture will equilibrate to give the same major product as was formed from kinetic reasons.
Although it has not been studied so far, if chiral ligands were used in the palladium catalyst, then this could be used as an example of asymmetric synthesis, and a single enantiomer of each diastereoisomer could be prepared. If this was successfully done, then the two diastereomers could be distinguished by optical rotation measurements.
References
- ↑ W. F. Maier, P. von R. Schleyer, "J. Am. Chem. Soc.", 1981, 103, 1891-1900: DOI:10.1021/ja00398a003
- ↑ P. Camps, F Perez, S. Vazquez, Tetrahedron, 1997, 53, 9727-9734: DOI:10.1016/S0040-4020(97)00595-4
- ↑ M. Gulias, R. Garcia, A. Delgado, L. Castedo, J.L. Mascarenas, J. Am. Chem. Soc., 2006, 128 (2), 384-385: DOI:10.1021/ja054487t
