Rep:Mod:pm3412p

Introduction

The transition state of a reaction can be defined as the state corresponding to the greatest potential energy along the entire reaction coordinate concerned. Upon reaching this point the species passes to form products, or falls back to reagents in the case of reversible reactions. Due to the nature of transition states they cannot be captured or studied directly, though their structure can be predicted from the Hammond Leffler Postulate. This states that the structure of the transition state resembles either the products or reagents, depending on which is closer in energy. A transition state that resembles the reactants is noted to be "early" and exists as an exothermic reaction, while a transition state that resembles the products is noted as "late" and exists as an endothermic reaction. While this postulate provides a generic structure of the transition state it is unable to give essential physical data, such as its energy, the bond lengths or angles.

For this reason computational chemistry has found wide use. A variety of different methods to find transition structures can be used on the Gaussview program, however only two shall be employed for this study. The first, and perhaps the easiest, shall be drawing the assumed transition state structure obtained from the Hammond Leffler Postulate and optimising this to a minimum. The optimisation process has several different levels of calculation can be used. The HF/3-21G level of theory is the quickest theory that was used, and produces an answer to a reasonable level of accuracy. A more advanced theory is the B3LYP/6-31G* which gives a much more accurate result at the cost of a longer computational time. The second method employed was the QST2 method. This involved drawing out the reagents and products observed in a reaction with a precise labeling scheme on all atoms. When run, the calculation will interpolate between these two species and find the associated transition state. As before the same level of calculations can be used with varying degrees of accuracy in the answer provided

This study shall be looking at the low energy minima of several different conformers of 1,5-hexadiene. These optimisations will then be utilisied to study the prefered reaction mechanism of the Cope Rearrangement by comparing the energies of the Chair and Boat transition state structures. Using the knowledge obtained from this, the pericyclic Diels-Alder reaction will be simulated and studied between a varied selection of molecules.

Cope Rearrangement Tutorial

Background Information

The Cope Rearrangement is a [3,3]-sigmatropic rearrangement isomerisation reaction of a 1,5-diene. This rearrangement can be seen in the diagram below. With the movement of 4n+2 electroncs (6), the thermally allowed reaction proceeds via Hückel topology with purely suprafacial components, resulting in a disrotation.

In most cases the product would be thermodynamically driven due to its greater stability, however in the 1,5-hexadiene example studied, due to symmetry, no such stability exists.

Optimisation of 1,5-hexadiene conformers using HF/3-21G theory

To begin a molecule of 1,5-hexadiene was drawn using the Gaussview program. The molecule was then subjected to different dihedral angles to produce either a gauche conformation (60 °) or an anti conformation (180 °). Within, 6 different gauche conformations and 4 different anti conformations have been studied.

In each conformation the optimisation log file shall be provided, along with the summary table produced. The structure will be shown to be at a stationary point from the log file produced by observing the convergence of the force and displacement vectors

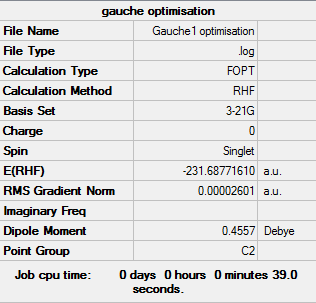
Gauche1

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000112 0.000450 YES RMS Force 0.000022 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000374 0.001200 YES Predicted change in Energy=-7.536908D-08 Optimization completed. -- Stationary point found.	Gauche1

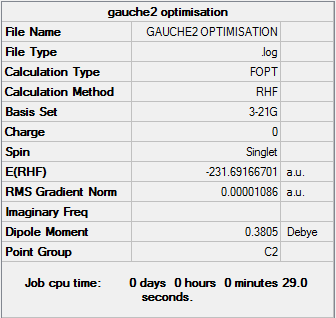
Gauche2

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.001118 0.001800 YES RMS Displacement 0.000331 0.001200 YES Predicted change in Energy=-1.009944D-08 Optimization completed. -- Stationary point found.	Gauche2

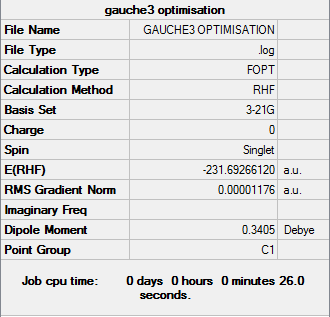
Gauche3

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.001138 0.001800 YES RMS Displacement 0.000326 0.001200 YES Predicted change in Energy=-2.568736D-08 Optimization completed. -- Stationary point found.	Gauche3

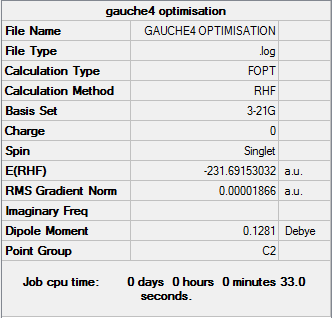
Gauche4

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001257 0.001800 YES RMS Displacement 0.000413 0.001200 YES Predicted change in Energy=-4.921094D-08 Optimization completed. -- Stationary point found.	Gauche4

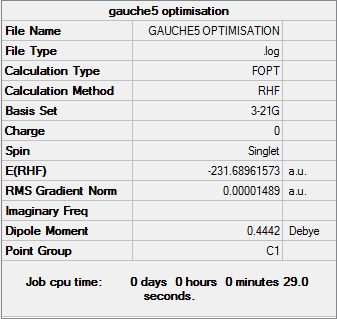
Gauche5

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.001072 0.001800 YES RMS Displacement 0.000334 0.001200 YES Predicted change in Energy=-3.411732D-08 Optimization completed. -- Stationary point found.	Gauche5

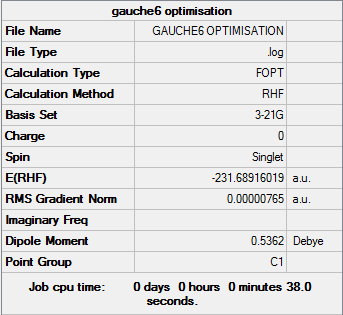
Gauche6

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.001585 0.001800 YES RMS Displacement 0.000399 0.001200 YES Predicted change in Energy=-7.443385D-09 Optimization completed. -- Stationary point found.	Gauche6

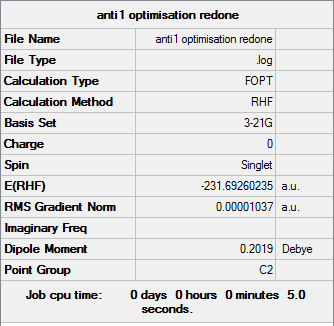
Anti1

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000026 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000555 0.001800 YES RMS Displacement 0.000172 0.001200 YES Predicted change in Energy=-2.945477D-08 Optimization completed. -- Stationary point found.	Anti1

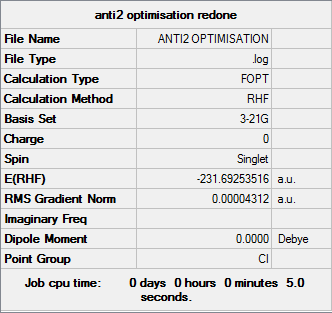
Anti2

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000110 0.000450 YES RMS Force 0.000022 0.000300 YES Maximum Displacement 0.001000 0.001800 YES RMS Displacement 0.000262 0.001200 YES Predicted change in Energy=-1.661248D-07 Optimization completed. -- Stationary point found.	Anti2

Anti3

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000053 0.000450 YES RMS Force 0.000015 0.000300 YES Maximum Displacement 0.000333 0.001800 YES RMS Displacement 0.000108 0.001200 YES Predicted change in Energy=-4.361668D-08 Optimization completed. -- Stationary point found.	Anti3

Anti4

Optimisation log file can be found here

Summary Data	Convergence	Jmol
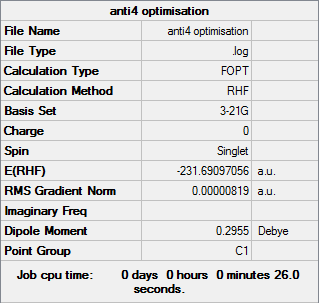	Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.001072 0.001800 YES RMS Displacement 0.000399 0.001200 YES Predicted change in Energy=-1.024078D-08 Optimization completed. -- Stationary point found.	Anti4

Comparison of HF/3-21G results

Conformer	Point Group	Energy (Hartrees)	Relative Energy (kcal/mol)
Gauche1	C2	-231.68771610	3.10
Gauche2	C2	-231.69166701	0.62
Gauche3	C1	-231.69266120	0.00
Gauche4	C2	-231.69153032	0.71
Gauche5	C1	-231.68961573	1.91
Gauche6	C1	-231.68916019	2.20
Anti1	C2	-231.69260235	0.04
Anti2	Ci	-231.69253516	0.08
Anti3	C2h	-231.68907063	2.25
Anti4	C1	-231.69097056	1.06

where 1 Hartree = 627.509 kcal/mol

By comparing the relative energies of the optimised structures, the conformation that would have the greatest abundance in a sample can be shown to be gauche3. Research has suggested that this minimum is the result of an attractive interaction between the C-C π orbital and a vinyl proton. Conversely the gauche1 conformer would represent the smallest proportion of conformers in a sample of 1,5-hexadiene. This conformer exhibits an exceedingly large amount of unfavourable repulsion due to the close distance of the two electron rich vinyl groups. Of the remaining gauche compounds relative energy is determined by the distance between opposing vinyl group protons. In general the greater the distance between the atoms, the lower the repulsion, and so the smaller the relative energy is. The anti conformer energies can be explained by comparing the vinyl proton to its distance from protons on the β carbon to it. For example the distance observed in the anti3 conformer is found to be the smallest at 2.41 Å explaining the high relative energy, while the anti1 and anti2 conformers have a similar separation of ~2.65 Å and so a similar relative energy.

Comparisons of HF/3-21G and B3LYP/6-31G*

The accuracy of the two theories can be directly compared by optimising the same molecule seperately and comparing physical properties obtained. The anti2 conformer shall be used for the optimisation. Below is the optimisation of the anti2 conformer using B3LYP/6-31G* theory

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000224 0.001800 YES RMS Displacement 0.000080 0.001200 YES Predicted change in Energy=-1.488104D-08 Optimization completed. -- Stationary point found.	Anti2

Using the labeling system on the diagram shown the following data was obtained.

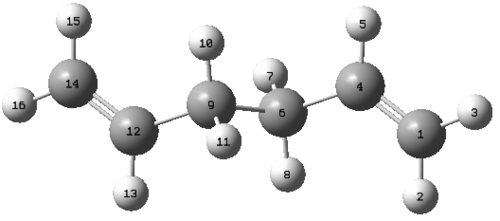
	Bond Lengths (Å)
Atoms	B3LYP	HF
C1-C4	1.33350	1.31618
C4-C6	1.50420	1.50882
C6-C9	1.54816	1.55317

By looking at bond lengths it can be seen that the B3LYP theory produces a significantly longer C1-C4 bond than is made in HF. This longer bond is more in line with measured literature values of 1.33 Å and so is a better theory for multiple bonds, however the C4-C6 and C6-C9 bonds are quite similar in both cases. When probing bond lengths in unsaturated compounds it is therefore more advantageous to use B3LYP, where as in saturated molecules it would be acceptable to use the HF/3-21G theory.

	Dihedral Angle (°)
Atoms	B3LYP	HF
C1-C4-C6-C9	118.599	114.626
C4-C6-C9-C12	180.000	180.000
C6-C9-C12-C14	-118.599	-114.626

Again there are specific advantages of using the B3LYP on unsaturated compounds when observing the dihedral angle. For a vinyl group the angle would be expected to be 120 °, typical of a sp² hydrised carbon centre. This value is more closesly achieved in the B3LYP theory for atoms C1-C4-C6-C9 and C6-C9-C12-C14 than it is in the HF theory producing a more accurate angle. (For a molecule such as chloroethene do you expect all the bond angles around the carbon atom to be 120º? Such ideal angle is a symmetry requirement, and is not an indication of the accuracy of a calculation. João (talk) 17:05, 17 February 2015 (UTC))

Frequency Analysis

When carrying out a frequency analysis we are finding the derivative of the optimised structure; or the second derivative of the potential energy surface (It is unclear what is meant here. Frequencies are related to the second derivative of the electronic energy/PES with respect to nuclear coordinate displacements/geometric changes. João (talk) 17:05, 17 February 2015 (UTC)). By performing a second derivative we are able to find out if the stationary points obtained from optimising the structure as a minimum or a maximum. Positive frequencies correspond to a minimum has been obtained, and negative frequencies (Even though they show up as negative numbers in the gaussian output, these frequencies are actually imaginary: think of the harmonic oscillator ω=(k/μ)^1/2, where k is the actual second derivative of the potential. João (talk) 17:05, 17 February 2015 (UTC)) correspond to a maximum. This is particularly useful when optimising transition states, as a single negative frequency should appear.

Below is the results of a frequency analysis on the anti2 conformer under B3LYP/6-31G*

Frequency log file can be found here

Summary Data	Thermochemistry values (Hartree)
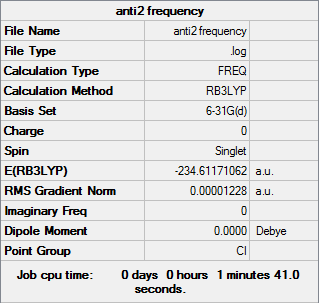	Sum of electronic and zero-point Energies= -234.469219 Sum of electronic and thermal Energies= -234.461869 Sum of electronic and thermal Enthalpies= -234.460925 Sum of electronic and thermal Free Energies= -234.500809

(How do these quantities vary with temperature? João (talk) 17:05, 17 February 2015 (UTC))

Analysis of the log file shows that all obtained frequencies are positive in magnitude and so the structure has indeed been optimised to a minimum energy. From the log file some important thermochemical values can be obtained, these are shown in the table above and will be further explored further on.

Optimising Chair and Boat transition structures

Before a chair or boat structure can be drawn out a fully optimised allyl fragment must be produced. Here the HF/3-21G theory will be sufficient. Below is the results of said optimision.

Optimisation log file can be found here

Summary Data	Convergence	Jmol
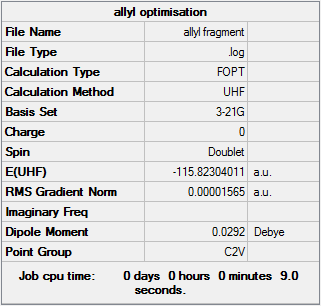	Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000150 0.001800 YES RMS Displacement 0.000058 0.001200 YES Predicted change in Energy=-4.857001D-09 Optimization completed. -- Stationary point found.	Allyl Fragment

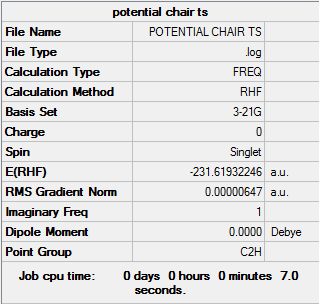
HF/3-21G Chair Optimisation

From this optimised allyl fragment I proceeded to make the chair transition state structure. The two fragments were placed in a staggered form approximately 2.2 Å apart from each other, put into the C_2h point group. The structure was then optimised and a frequency analysis performed using the HF/3-21G level of theory. However as a transition state structure was being observed optimisation was changed from "minimum" to "TS (Berny)". Below are the results of the calculation

Opt+Freq log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000397 0.001800 YES RMS Displacement 0.000128 0.001200 YES Predicted change in Energy=-1.474229D-08 Optimization completed. -- Stationary point found.	Chair TS structure

Upon opening the log file a successfully formed chair structure was produced. As shown in the convergence section the value tend towards a stationary point. To determine the nature of this point the frequencies obtained must be analysed from the log file produced. It can be seen that all values of frequency are positive except one, with a value of -817.93 cm^-1. The presence of a negative value of a second derivative tells us that the stationary point is a maximum, to be expected of a TS structure that occurs at a maximum on the potential energy surface. (It is a maximum along one particular direction, the molecular distortion animated bellow, it is a minimum with respect to any other distortion. Such a shape has the name of saddle point (think of a horse saddle or a Pringles crisp). João (talk) 17:05, 17 February 2015 (UTC))

Reaction Pathway Vibration

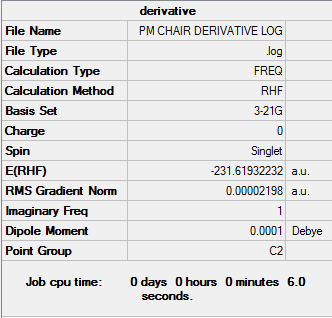
Frozen Coordinates Chair Optimisation

A different method that can be employed is the froze coordinate method. In this method constraints are applied to the input structure before optimisation. Similiar to the input file of the HF/3-21G optimisation the fragments were seperated by 2.2 Å. This method however allowed the distance of the terminal ends of the allyl fragments to be fixed to 2.2 Å during the optimisation process, while the rest of the molecule is free to be optimised. From this optimised structure, the molecule was reoptimised, this time with the terminal ends unfixed and the rest of the molecule fixed to their optimised distance (The rest of the molecule is not frozen at this stage. However, most of the optimization has been done, and they may move little. João (talk) 17:05, 17 February 2015 (UTC)). Below is the results of the process performed.

Opt+Freq log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000075 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.001503 0.001800 YES RMS Displacement 0.000378 0.001200 YES Predicted change in Energy=-1.573078D-07 Optimization completed. -- Stationary point found.	Chair TS structure

Comparing these two methods shows that similar bond lengths are obtained, with the frozen coordinate method yielding slightly longer bonds (2.02073 compared to 2.02034), and a similar frequency value, with the frozen coordinate method producing a larger number (-817.88) compared to the HF/3-21G method (-817.93). (You are using the HF/3-21G level of theory in both cases. And what do you conclude from these structural similarities? João (talk) 17:05, 17 February 2015 (UTC))

QST2 Boat Optimisation

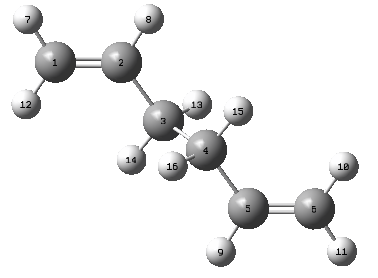
A different method is employed for the optimisation of the boat structure that was previously mentioned during the introduction. The QST2 method involved the drawing of the reagents and the products with precise labeling to show the Cope Rearrangement. When run the method will interpolate the two structures and find the transition state. The following labeling system was used for the structures

Reagent Numbering	Product Numbering

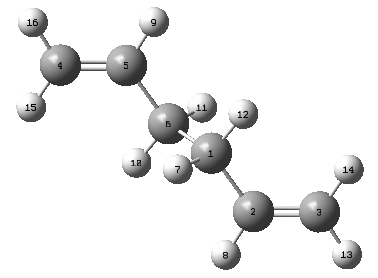
Using these structures and number systems a QST2 calculation was run using the HF/3-21G, however this resulted in the transition state to adopt the wrong structure. It seems that rather than the Cope Rearrangement occuring the C3-C4 bond had broke, forming two allyl fragments, followed by translation to form a chair structure as shown below.

In order to counteract this unfavourable transition state (Why unfavourable? João (talk) 17:05, 17 February 2015 (UTC))new structures were made that involved a rotation around the C3-C4 bond, to encourage the Cope Rearrangement to be modeled.

Reagent Numbering	Product Numbering

Using these structures the same calculation was rerun to successfully form the boat transition state structure. Below are the results.

Opt+Freq log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000093 0.000450 YES RMS Force 0.000031 0.000300 YES Maximum Displacement 0.001736 0.001800 YES RMS Displacement 0.000493 0.001200 YES Predicted change in Energy=-5.228362D-07 Optimization completed. -- Stationary point found.	Boat TS structure

This stationary point can be shown to be a maximum from analysis of the frequency table. A vibration at -840.01 cm^-1 shows the state is a maxima and corresponds to the Cope rearrangement

Reaction Pathway Vibration

IRC

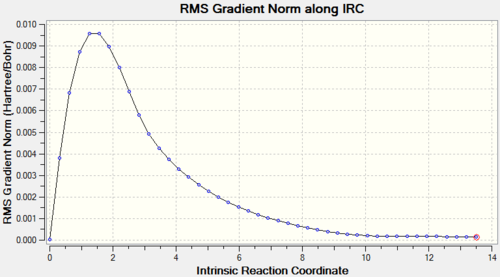
A question one may ask when modelling the transition states is "What conformer is initially produced following the Cope Rearrangement?" This calculation is possible on Gaussview by running the IRC method on an already optimised transition state structure. The accuracy of this result is directly proportional to the number of points recorded (It is not so much the total number of points, but rather the step size at each iteration. João (talk) 17:05, 17 February 2015 (UTC)), 50 points was deemed satisfactory for this reaction. As our reaction is symmetrical, (both the reagent and product have the exact same structure), only the forward direction reaction coordinate will be calculated to ease the computational work load asked. From the log file produced by calculation of the chair transition state, an IRC graph can be visualised containing two elements, a total energy plot and a RMS plot.

The total energy plot shows how the high energy transition state, shown at coordinate 0, rolls down the potential energy surface towards the minimum of the system available. Analysis of the RMS plot shows the derivative of the total energy plot, and that a minimum has indeed been obtained at step 44 where the value has tended towards 0, indicating the conformer product. Opening of the checkpoint file visualises the structure produced at step 44, which is of striking similarity to the gauche2 conformer. It can therefore be concluded that upon undergoing the Cope Rearrangement in the chair transition state, the initial conformer produced is gauche2.

Activation Energies

Given all the data calculated so forth, and using anti2 as a reference, the activation energy of the transition states can be found. Both the HF/3-21G and the B3LYP/6-31G* levels will be examined, so the chairs and boats must be reoptimised at the B3LYP level.

Chair transition state optimisation (B3LYP)

Opt+Freq log file can be found here

Summary Data	Convergence
	Item Value Threshold Converged? Maximum Force 0.000026 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000102 0.001800 YES RMS Displacement 0.000033 0.001200 YES Predicted change in Energy=-4.975418D-09 Optimization completed. -- Stationary point found.

Boat transition state optimisation (B3LYP)

Opt+Freq log file can be found here

Summary Data	Convergence
	Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000171 0.001800 YES RMS Displacement 0.000055 0.001200 YES Predicted change in Energy=-3.514336D-09 Optimization completed. -- Stationary point found.

(Are the optimized transition state geometries at both levels of theory very different? At the higher level of theory do they still correspond to a transition state? João (talk) 17:05, 17 February 2015 (UTC))

The thermochemical data obtained inside each optimised log file is tabulated below, with all units measured in Hartrees.

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K
Chair TS	-231.619322	-231.466700	-231.461341	-234.556932	-234.414879	-234.408951
Boat TS	-231.602802	-231.450928	-231.445299	-234.543093	-234.402342	-234.396008
Reactant (Anti2)	-231.692535	-231.539539	-231.532566	-234.611711	-234.469219	-234.461869

The activation energies can then be calculated by subtracting the appropriate energy away from the appropriate Anti2 energy. Below are the activation energies for both the chair and boat transition states relative to the anti2 conformation in HF/3-21G and B3LYP/6-31G* measured in kcal/mol

	HF/3-21G		B3LYP/6-31G*		Expt.
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE (Chair)	45.71	44.69	34.10	33.21	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.33	44.7 ± 2.0

Several points can be deduced from examination of the activation energy. It is apparent that by using the B3LYP/6-31G* theory a value is obtained that is much closer to that of experimentally observed values than the HF/3-21G theory.

It can also be seen that when performed at 0 K, in both theories, the amount of energy required to reach the transition state is slightly greater. This arises from the lack of thermal energy present in the surroundings causing the minima to be lower than at room temperature. (It is not so much that the minimum is lower, but that without thermal energy the molecule is "closer" to the minimum. João (talk) 17:05, 17 February 2015 (UTC))

However from analysis of the calculated activation energies, in both levels of theory, the chair transition state occurs at a lower energy, and is therefore the followed pathway.

The Diels Alder Cycloaddition

Background Information

The Diels–Alder reaction is a concerted 4+2 suprafacial cycloaddition between a conjugated diene and a dienophile, to form a cyclohexene system. It has found wide application in synthetic chemistry due to the versatility of reagents that can be used, and products that can be produced. Below is the general reaction scheme

This reaction is driven by the formation of two new σ bonds, which are energetically more stable than the π bonds broken.

Ethylene/cis-butadiene Diels Alder reaction

To begin, a molecule of cis-butadiene was built and optimised to the AM1 semi-empirical level of theory. Below are the results of said calculation

Cis-Butadiene optimisation

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000407 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-9.691193D-09 Optimization completed. -- Stationary point found.	Cis-Butadiene

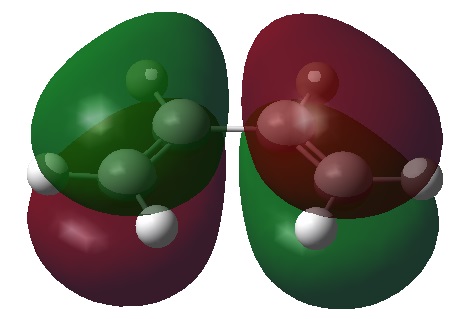
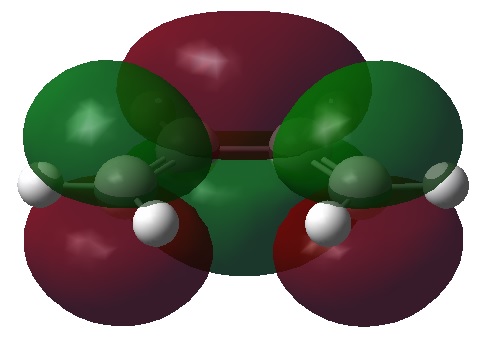
From this optimised structure it is possible to visualise the HOMO and LUMO orbitals for cis butadiene. The results of such visualisation are shown in the table below.

HOMO orbital	LUMO orbital
Antisymmetric with respect to the plane	Symmetric with respect to the plane

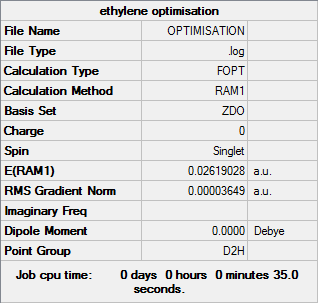
Ethylene optimisation

To model the ethylene/cis-butadiene transition state, ethylene must be optimised to the same level of theory as the optimised cis-butadiene

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000178 0.000450 YES RMS Force 0.000053 0.000300 YES Maximum Displacement 0.000440 0.001800 YES RMS Displacement 0.000238 0.001200 YES Predicted change in Energy=-4.401461D-08 Optimization completed. -- Stationary point found.	Ethylene

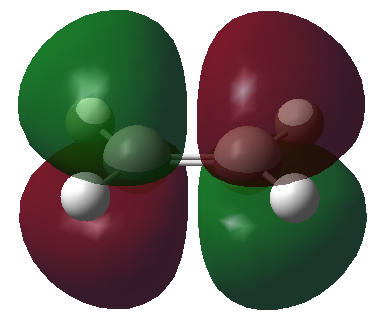
The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
Symmetric with respect to the plane	Antisymmetric with respect to the plane

Transition State Structure Optimisation

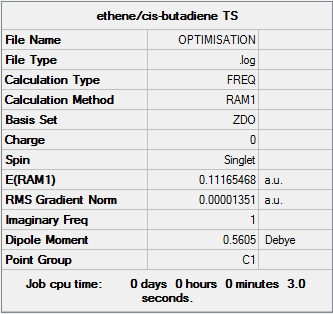
The optimised geometries of ethylene and cis-butadiene were inserted and seperated at a distance of 2.2 Å between terminal ends and constrained to a C₁ point group (<span style="color:gray"<The C₁ point group actually corresponds to the absence of symmetry João (talk) 17:05, 17 February 2015 (UTC)). This distance resulted in a failed optimisation.I it is likely that the distance was too great, and only repulsive forces were felt between the two molecules, explaining the apparently ejected ethylene molecule. A closer distance of ~ 2.14 Å was used and calculated. This optimisation was successful, and below are the results.

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000035 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.001659 0.001800 YES RMS Displacement 0.000426 0.001200 YES Predicted change in Energy=-3.088465D-08 Optimization completed. -- Stationary point found.	Ethylene/Cis-Butadiene TS

Analysis of Diels Alder reaction

Geometric information of the transition state studied is shown in the table provided, using the labeling system to the right

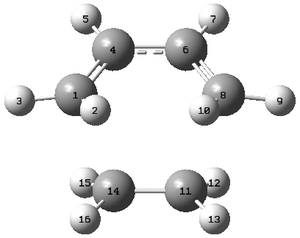
Atoms	Bond Lengths (Å)
C1-C4	1.38187
C4-C6	1.39750
C8-C11	2.11922
C11-C14	1.38290
C1-H2	1.10079
C1-H3	1.09888
C4-H5	1.10184
C11-H12	1.09964
C11-H13	1.10023

Typically, a sp³ C-C bond length is 1.54 Å, while a sp² C-C bond is 1.46 Å. (So what do you conclude? João (talk) 17:05, 17 February 2015 (UTC)) The van der Waals radii of a carbon atom has been shown in literature to be 1.70 Å. As the distance between the forming bond (C8-C11) is less than twice the van der Waals radii for carbon, an attractive interaction exists and so the formation of a σ C-C bond is favoured.

It has already been shown that the optimisation process for the ethylene/cis-butadiene converged towards a stationary point in the summary table provided. To check if this point is a maximum, and therefore a transition state, the table of vibrations must be consulted. As a negative vibration was produced at -956.32 cm^-1 the stationary point is indeed a maximum. This vibration corresponds to the Diels-Alder reaction and is animated below:

Reaction Pathway Vibration

It can be seen from this animation that the Diels-Alder reaction proceeds by a concerted synchronous bond formation process. The lowest positive frequency shows some rotational motion of the ethylene molecule with little movement from the cis-butadiene.

Lowest Positive Frequency

As the motion is not in the direction of bond formation it is unlikely however that this is involved in the reaction. It could hypothetically be the first observed vibration in the cyclohexene product molecule (Why would it be the first vibration to be observed? João (talk) 17:05, 17 February 2015 (UTC)), however this cannot be validated unless additional calculations are performed, which is outside the scope of this study.

By modelling orbitals of the transition state and reagents, particularly the HOMO and LUMO, it can be found if a reaction is allowed to occur or not. The requirements for this are as follows.

"If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed"

(This statement is a bit vague. Can it be made more formal? João (talk) 17:05, 17 February 2015 (UTC))

Using this knowledge we can determine if the reaction of ethylene and cis-butadiene is allowed.

HOMO orbital	LUMO orbital
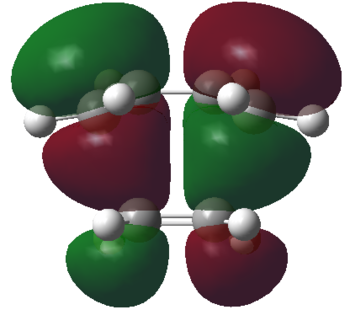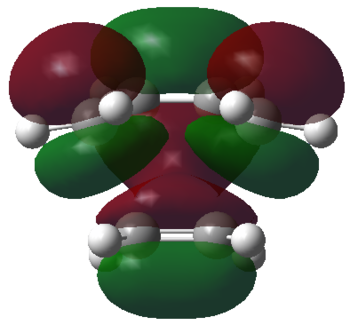
Antisymmetric with respect to the plane	Symmetric with respect to the plane

By deconstructing the HOMO of the transition state structure we can see that it consists of the LUMO of ethylene, and the HOMO of cis-butadiene. Similarly deconstructing the LUMO of the transition state structure yields the HOMO of ethylene and the LUMO of cis-butadiene. The Diels-Alder cycloaddition reaction between ethylene and cis-butadiene is therefore allowed.

Cyclohexa-1,3-diene/Maleic Anhydride Diels Alder reaction

Cyclohexa-1,3-diene optimisation

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.001475 0.001800 YES RMS Displacement 0.000427 0.001200 YES Predicted change in Energy=-5.944163D-09 Optimization completed. -- Stationary point found.	Cyclohexa-1,3-diene

The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
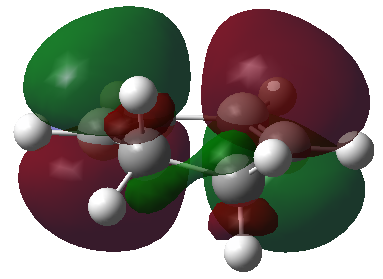Antisymmetric with respect to the plane	Symmetric with respect to the plane

Maleic Anhydride optimisation

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000294 0.000450 YES RMS Force 0.000086 0.000300 YES Maximum Displacement 0.001068 0.001800 YES RMS Displacement 0.000421 0.001200 YES Predicted change in Energy=-3.973175D-07 Optimization completed. -- Stationary point found.	Maleic Anhydride

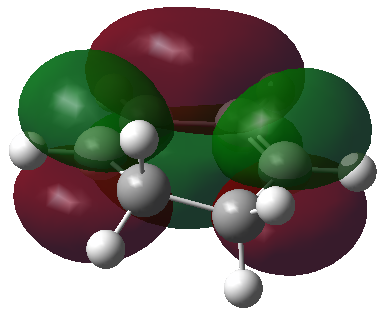
The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
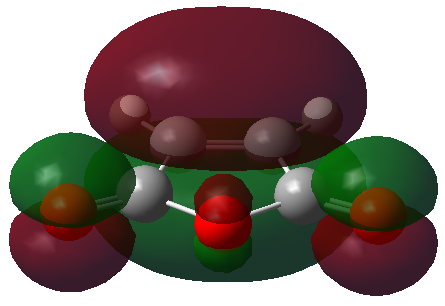Symmetric with respect to the plane	Antisymmetric with respect to the plane

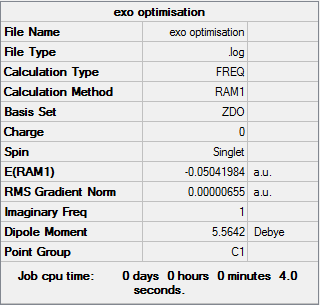
Exo Transition State optimisation

The optimised geometries of cyclohexa-1,3-diene and maleic anhydride were inserted and seperated at a distance of 2.1 Å in an exo formation. Initial optimisation attempts resulted in the severe repulsion of the two groups from each other as shown on the right. To counteract this the C₂H₄ bridge was placed at an altered angle to better accommodate the proposed structure. This resulted in a successful optimisation and the results are shown in the table below

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000020 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000598 0.001800 YES RMS Displacement 0.000080 0.001200 YES Predicted change in Energy=-8.236491D-09 Optimization completed. -- Stationary point found.	Exo Transition State

This stationary point is found to be a maximum by examining the table of vibrations. As a negative vibration was produced at -812.24 cm^-1 the stationary point is of the transition structure. This vibration corresponds to the Diels-Alder reaction and is animated below:

Exo Reaction Pathway Vibration

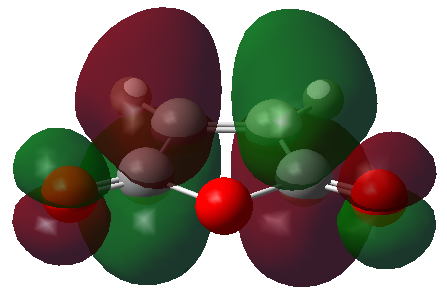
The HOMO and LUMO orbitals of the optimised TS have been visualised in the table below.

HOMO orbital	LUMO orbital
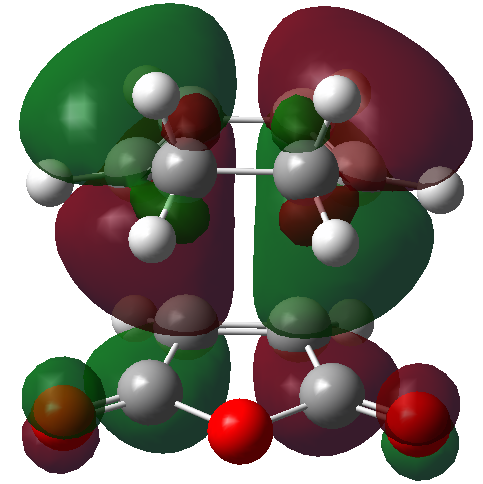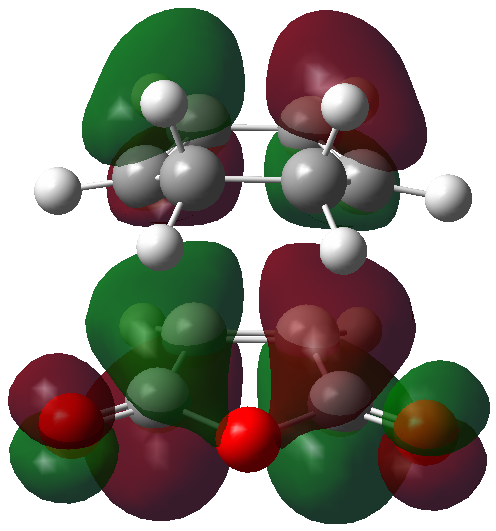
Antisymmetric with respect to the plane	Antisymmetric with respect to the plane

Endo Transition State optimisation

The optimised geometries of cyclohexa-1,3-diene and maleic anhydride were inserted and seperated at a distance of 2.1 Å in an endo formation. The optimisation results are shown in the table below

Optimisation log file can be found here

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.001108 0.001800 YES RMS Displacement 0.000206 0.001200 YES Predicted change in Energy=-1.466125D-08 Optimization completed. -- Stationary point found.	Endo Transition State

This stationary point is found to be a maximum by examining the table of vibrations. As a negative vibration was produced at -806.39 cm^-1 the stationary point is of the transition structure. This vibration corresponds to the Diels-Alder reaction and is animated below:

Endo Reaction Pathway Vibration

The HOMO and LUMO orbitals of the optimised molecule have been visualised in the table below.

HOMO orbital	LUMO orbital
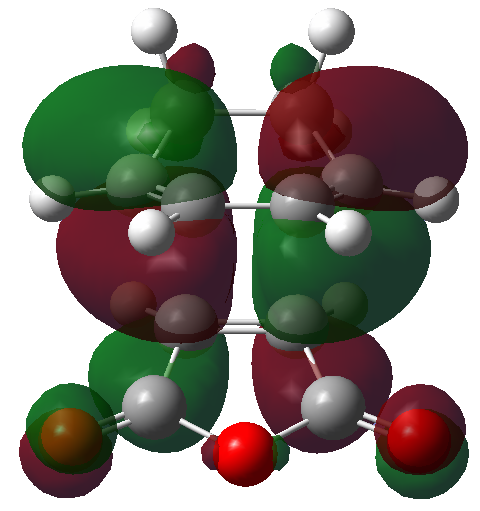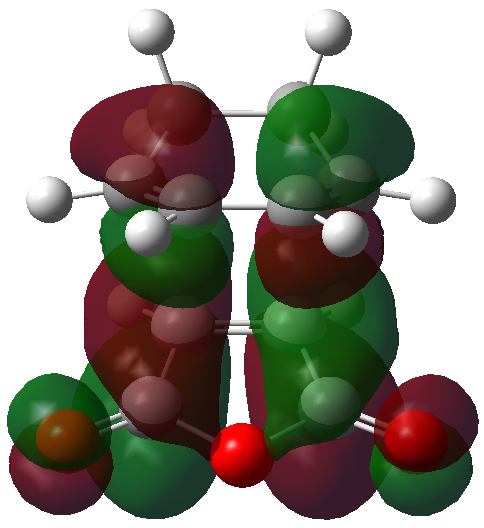
Antisymmetric with respect to the plane	Antisymmetric with respect to the plane

Comparisons of Transition State Structures

Energies of conformers

Conformer	Energy (Hartrees)	Relative Energy (kcal/mol)
Exo	-0.05041984	0.68
Endo	-0.05150479	0

By examination of the transition states, optimised to the same level of theory, it can be seen that the endo conformation is of lower energy. As this conformation is at a lower energy, the endo conformer is the kinetic product of the 4+2 cycloaddition reaction. It can be deduced that the endo conformer of this reaction will form the largest percentage of product. (This will surely depend on reaction conditions. What does "kinetic product" mean? João (talk) 17:05, 17 February 2015 (UTC))

Geometric Analysis

Exo

Atoms	Bond Lengths (Å)
C1-C2	1.48975
C2-C9	1.39439
C9-C11	1.39677
C1-C4	1.52209
C2-C16	2.17027
C16-C17	1.48820
C17-O23	1.40963
C17-O21	1.22054
C1-C17	2.94517

Endo

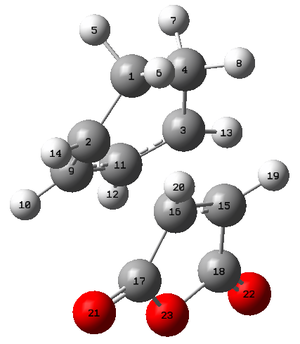
Atoms	Bond Lengths (Å)
C1-C2	1.49053
C2-C9	1.39307
C9-C11	1.39725
C1-C4	1.52297
C2-C16	2.16237
C16-C17	1.48923
C17-O23	1.40896
C17-O21	1.22057
C9-C17	2.89223

It can be seen that the length of the forming σ bonds are different in the endo and exo form, with the exo transition state have a bond that is longer than the equivalent endo bond length. This is reflected in the longer distance between C1 and C17. The steric repulsion between these two fragments has caused the exo conformer to adopt a much longer distance in order to alleviate some of this unfavourable energy. Because of this greater distance it is likely that the maleic anhydride ring will be more strained than the endo counterpart, that is able to abopt a much closer transition state.a much greater distance between the two species.

By opening the associated log files and examining the "Thermochemistry" section the follow energy of molecules at 298.15 K in hartree can be obtained:

Molecule	Semi-empirical/AM1 Sum of electronic and thermal energies at 298.15 K
Cyclohexa-1.3-diene	0.157726
Maleic Anhydride	-0.058197
Exo	0.144881
Endo	0.143684

From these data it can be found that the activation energy of the exo transition state is 28.46 kcal/mol, while the activation energy of the endo transition state is 27.71 kcal/mol. This reinforces the idea previously asserted that the endo conformer is the kinetic product due to the lower energy barrier of reaction.

Secondary Orbital Overlap effect

It is possible, such as in the Ethylene/Cis-butadiene example, to deconstruct the transition state MO's and obtain the associated reagent orbitals, which can then be used to show whether the reaction can occur. However from looking at the transition state orbitals obtained it is clear that this is not feasible to do (Why not? One may have to look beyond the frotier orbitals though. João (talk) 17:05, 17 February 2015 (UTC)). This does not mean that the reaction does not occur when performed, experimentation has shown the reaction can be carried out. It is more likely that the level of theory that was used is not sufficient enough to produce credible molecular orbitals that follow Frontier Molecular Orbital Theory (Or that the frontier orbital model has its limitations and cannot be applied in this case. João (talk) 17:05, 17 February 2015 (UTC)), and so in order to better probe this the section must be re-performed using a better level of theory, such as B3LYP/6-31G*.

(What is the secondary orbital overlap effect? João (talk) 17:05, 17 February 2015 (UTC))

Conclusion

In this study the mechanism of the Cope Rearrangement and the Diels-Alder reaction were investigated using Gaussian. From optimised conformers of 1,5-hexadiene the chair and boat transition states were modeled to different levels of theory, some objectively better than others, such as B3LYP/6-31G*. While initially the boat optimisation resulted in a failure, this was amended by alteration of the dihedtral angle and resulted in a successful optimisation. It was shown that these transition states were maxima by the presence of a negative imaginary frequency, corresponding to the Cope Rearrangement. The result of the rearrangement on the chair transition state was shown to produce the gauche2 conformer by calculation of the PES. To conclude this section the activation energy of each transition state was calculated, and shown to have a remarkably good agreement with experimental values in the case of B3LYP/6-31G*, while not so much with HF/3-21G.

From using the knowledge applied in the Cope Rearrangement, the Diels-Alder reaction was modeled. In each study an orbital analysis was performed, however in the case of the Cyclohexa-1,3-diene/Maleic Anhydride cycloaddition this was not possible. It is likely that the Frontier Molecular Orbital Theory fails for a system this complex when using the less accurate semi-empirical/AM1 level of theory. However sufficient data was produced that allowed for the calculation of activation energies and geometric analysis.

Given more time the effects of asymmetric dienes in the Cope Rearrangement could be studied, and the resulting stereochemistry be examined. The Diels-Alder rearrangement would be redone, but at a higher level of theory, such as B3LYP/6-31G* to produce more accurate results. If these results agree with literature then a wider variety of molecule would be modeled to show the importance and reliability of computational calculations of chemical reactions.