Rep:Mod:pks1927
Module 1: Structure and Spectroscopy (Molecular Mechanics/Molecular Orbital Theory)
Introduction
Plastic modelling kits are used to understand the 3D structures of molecules and how these structures can affect chemical reactivity. These models have also been used to analyse molecular properties, such as, sterics and stereoselectivity. However, these modelling kits do not provide quantitative data for molecular properties. Quantum mechanical models have been designed to solve this problem, but these models are time consuming, complicated and produce results which can be inacurate by 4-20 kJmol-1.
Molecular mechanics (MM) is a non-quantum mechanical model, which can predict several molecular properties with the same accuracy as quantum mechanical methods. MM conveys that the energy of a molecule is the sum of five individual bond properties: bond stretching; bond angle; bond torsions; non-bonding van der Waal repulsions and electrostatic interactions.
MM2 and MMFF94 force fields present in ChemBio3D were used to complete the following exercises . However, there are limitations to these MM models because if the molecule under consideration cannot be related to simpler diatomics then the summation used to produce a value for the total energy of the molecule cannot be obtained. Only small hydrocarbons can be analysed by MM models . In addition, the model cannot be used to analyse transition states as this involves studying bond breaking which is not possible.
Cyclopentadiene Dimers
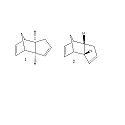
Cyclopentadiene can dimerise and form an exo dimer (molecule 1) or an endo dimer (molecule 2). The dimer that is the major product is the endo dimer (molecule 2).
 |
 |
 |
The Hydrogenation of Cyclopentadiene Dimers
The endo dimer can undergo hydrogenation to form one of the dihydro derivatives 3 or 4. After continuous hydrogenation a tetrahydro derivative can be produced.
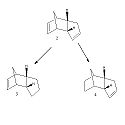 |
 |
 |
| Type of Energy kcalmol-1 | Exo Cyclopentadiene Dimer | Endo Cyclopentadiene Dimer | Molecule 3 | Molecule 4 |
|---|---|---|---|---|
| Stretch | 1.29 | 1.26 | 1.24 | 1.11 |
| Bend | 20.59 | 20.83 | 18.90 | 14.54 |
| Stretch-Bend | -0.84 | -0.84 | -0.76 | -0.55 |
| Torsion | 7.67 | 9.52 | 12.19 | 12.48 |
| Non-1,4 VDW | -1.44 | -1.55 | -1.53 | -1.06 |
| 1,4 VDW | 4.23 | 4.34 | 5.74 | 4.50 |
| Dipole-Dipole | 0.38 | 0.45 | 0.16 | 0.14 |
| Total Energy | 31.88 | 34.00 | 35.94 | 31.16 |
| Total Energy kJ/mol-1 | 133.39 | 142.27 | 150.37 | 130.39 |
Explanation/Theory for Dimerisation of Cyclopentadiene
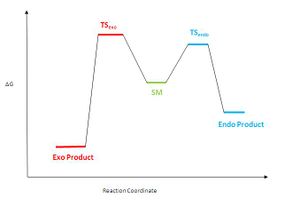
The dimerisation of cyclopentadiene is a self Diels-Alder reaction, which can be controlled kinetically and thermodynamically. Under thermodynamic control the reaction is in equilibrium and the product that predominates is the most stable one. Under kinetic control reactions tend to be irreversible and the product with the smallest activation barrier (lowest energy transition state) forms.
It was stated that when cyclopentadiene dimerises it forms specifically the endo product. The endo dimer is higher in energy than the exo one and hence is the kinetic product (see table). Therefore the dimerisation must be under kinetic control. If the dimerisation of cyclopentadiene was under thermodynamic control, the exo dimer would have predominated. A small amount of the endo product will also have be produced because the reaction will be in equilibrium and hence the exo dimer can convert back to the starting material and then form the endo dimer (see diagram on left).
Under kinetic control the dimer that forms faster predominates. The energy barrier to form the transition state, which leads to the formation of the endo dimer is much smaller than the activation energy barrier needed to be overcome to form the exo dimer (see diagram on left) and hence the endo dimer forms faster.
For both dimers the major contribution to the total energy of the molecules is the 'bend' component. The values for this component are fairly large and positive and hence convey that the bond angles have deviated significantly from normality. These deviations are due to steric hindrance experienced by the molecules. The endo dimer has a slightly larger value for the 'bend' component than the exo dimer and hence the endo product is under more steric hindrance and thus less stable.
Explanation/Theory for Hydrogenation of Endo Dimer
Molecules 3 and 4 are produced when the endo cyclopentadiene dimer undergoes hydrogenation. Molecule 4 is more stable than molecule 3 as it has a lower total energy and therefore must be the thermodynamic product. The total energy for both molecules is a sum of several components (see table), but the components do not contribute equally to the total energy. For both molecules the bending term contributes the most, then the torsion term, then the stretching term, the van der Waals term and finally the H-bonding term contributes the least to the total energy. This means that both molecules experience a lot of steric hindrance and strain, which causes the bond angles of the molecules to deviate from normality.
The difference in the total energy for both molecules is due to the fact that the bending component and van der Waals component for molecule 3 is larger than in molecule 4. This means that molecule 3 is under more strain and steric hindrance than molecule 4 and hence is less stable.
This is because double bonds contain sp2 hybridised orbitals which prefer a bond angle of 120o, but the double bond angle in molecule 3 is 107.6o. The double bond angle in molecule 4 is 112.5o. As the angle in molecule 3 has deviated much more from normality compared to the angle in molecule 4, it is more strained and less likely to form as it is higher in energy (kinetic product).
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
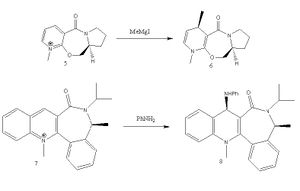
Two nucleophilic reactions are being investigated in this section. Firstly, an optically active derivative of prolinol (5) is reacted with a grignard reagent (methyl magnesium iodide) to form molecule 6. Secondly, the pyridium ring in molecule 7 reacts with aniline to form molecule 8, which then can be used to transfer NHPhenyl groups to electrophilies like carboxylic acids.
Mechanism for the Nucleophilic Addition of Prolinol
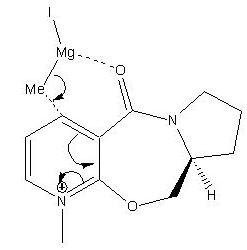
The reaction between molecule 5 (optically active prolinol) and the Grignard reagent (methyl magnesium iodide) is highly regio and stereoselective. This is because the pyridinium ring of molecule 5 can be alkylated at the 4 position or at the 6 position. However, alkylation at the 4 position predominates because molecule 6 is formed (see equation). Methyl magnesium iodide is quite selective as the ratio of the 4 position and 6 position products produced with this Grignard reagent is 19:1. However, if bulkier Grignard reagents are used in this reaction the regio-selectivity is increased as the ratio of the regioisomers that form is > 99:1.[1]
This reaction is also very stereoselective as the methyl group that is added to the pyridinium ring can be above or below the plane of the ring. However, the methyl group predominantly is added above the ring (see molecule 6). The reason for this is that the carbonyl group in molecule 5 is slightly above the plane of the ring (10o) and hence when the magnesium of the Grignard reagent coordinates to the carbonyl to form a six membered ring transition state and the methyl of the Grignard reagent is also be above the plane of the ring. Therefore the methyl group must attack the pyridinium ring from above and hence must bond to the ring from above the plane (see mechanism on the left).
Mechanism for the Nucleophilic Addition to the Pyridinium Ring of Molecule 7
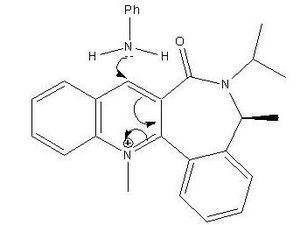
The nucleophilic reaction between molecule 7 and aniline is also stereoselective. The carbonyl group is 20o above the plane of the ring in molecule 7. This causes the nucleophile (aniline) to attack from below the plane of the pyridinium ring of molecule 7 and hence bind to the pyridinium ring from below. This stereochemistry occurs because aniline is a bulky group and hence if it attacked the pyridinium ring from above it would 'clash' with the carbonyl and hence cause steric hindrance, which is destabilising. The steric hindrance is minimised when the aniline attacks from below the plane of the ring. The methyl group on the seven membered ring is in the same plane as the NHPhenyl group in molecule 8, but the isopropyl group is in the opposite plane to the NHPhenyl group. This configuration minimises the steric hindrance in molecule 8 and hence lowers the total energy of the molecule. The molecule still experiences some sterics due to the isopropyl and carbonyl group being in the same plane.[2]
Results/Analysis
Using the MMFF94 force field in ChemBio3D, the total energies of molecules 5, 6, 7 and 8 were found to be 57.43, -2.65, 98.38 and 38.21 kcalmol-1 (240.3, -11.1, 411.6 and 159.9 kJmol-1) respectively. The MM2 force field was also used to deduce the total energies of molecules 5-8 and the values obtained are shown in the table below. The values are fairly different to the ones obtained by using the MMFF94 force field. The values should not be compared as different force fields yield different answers as the methods used by each force field is different and so the large differences between the values obtained by MMFF94 and MM2 do not suggest that the procedures are incorrect.
| Type of Energy kcalmol-1 | Molecule 5 | Molecule 6 | Molecule 7 | Molecule 8 |
|---|---|---|---|---|
| Stretch | 2.04 | 2.24 | 3.97 | 4.11 |
| Bend | 14.30 | 16.30 | 11.51 | 18.23 |
| Stretch-Bend | 0.13 | 0.35 | 0.41 | 0.81 |
| Torsion | 5.01 | 5.70 | 9.96 | 5.07 |
| Non-1,4 VDW | -0.52 | -0.29 | 3.47 | 2.22 |
| 1,4 VDW | 16.55 | 17.52 | 29.41 | 34.03 |
| Charge/Dipole | 9.56 | - | 9.89 | - |
| Dipole/Dipole | -4.01 | -4.30 | -4.89 | -6.66 |
| Total Energy | 43.05 | 37.53 | 63.73 | 57.80 |
| Total Energy/ kJmol-1 | 180.14 | 157.01 | 266.65 | 241.83 |
The total energies obtained for molecules 5 to 8 by using MM2 force field show that the 'bend' and the 1,4 VDW components contribute to most of the total energies. The bend and 1,4 VDW components are positive and large which indicate that the bond angles and intermolecular forces have deviated from normality. In molecules 5 and 7 the carbonyl group was slightly above the plane of the ring (10o and 20o respectively).
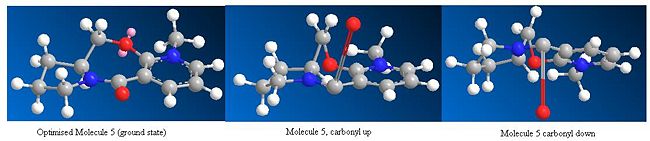
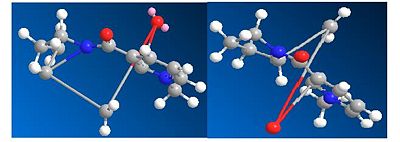
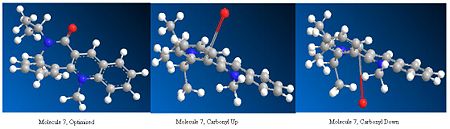
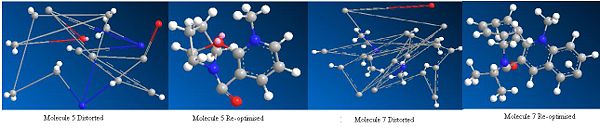
Once the optimised geometries for molecules 5 and 7 were found the carbonyl position in these molecules was changed and the molecule was re-optimised to get the minimum total energy again. The carbonyl was moved above the plane of the ring and below the ring for both molecules. The total energy obtained after re-optimisation did not change for either molecule. The angle of the carbonyl group with respect to the ring were also did not change for both molecules. This shows that the optimised geometries obtained for molecules 5 and 7 are the ground state configuration.
The O and CH2 in the seven membered ring in molecule 5 were also moved around and then these structures were re-optimised and again the total energies of the molecules and the angle of the carbonyl did not change. This shows that if you start with the molecule in strange orientation it will be optimised to the ground state configuration.
However, in both molecules 5 and 7 if the molecule is completely distorted by changing the positions of the atoms in the aromatic rings, the re-optimisation produces a higher energy molecule, which has a completely different geometry to the ground state molecule. For molecule 5 the total energy after re-optimisation of the distorted structure was 626.5 kcalmol-1 (2621 kJmol-1) using MM2 and 716.4 kcalmol-1 (2997 kJmol-1) using MMFF94. For molecule 7 the total energy after re-optimisation of the distorted structure was 401.5 kcalmol-1 (1680 kJmol-1) using MM2 and 99.6 kcalmol-1 (416.7 kJmol-1) using MMFF94.
 |
 |
 |
 |
The Grignard component was not included when the energy was calculated for molecule 5 as ChemBio3D does not have the element magnesium in its programme and therefore the calculations cannot be run. The models MM2 and MMFF94 do not take into account bond breaking and hence are poor models to use as bond breaking occurs in both the reactions described above. Better models that can be used are the MOPAC interface and Gaussian interface which are used below
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
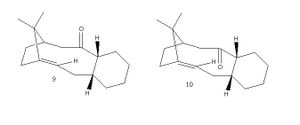
Taxol is a very important drug, which is used as one of the treatments of ovarian cancer. The synthesis of taxol was first proposed by Paquette, where 9 and 10 are key intermediates to this synthesis. Molecule 9 has the carbonyl pointing upwards and the cyclohexane ring adopts a twist chair boat configuration. Molecule 10 has the carbonyl pointing downwards and the cyclohexane ring is in a chair configuration. Both these intermediates isomerise to an alternative carbonyl isomer and this is an example of atropisomerism. This is where isolation of distinct stereoisomers can occur, due to the hindered and restricted rotation about a bond, which is often caused by high steric demand.[3]
In order to deduce the energies of the two isomers and hence find out which intermediate is most likely to predominate, the structures were drawn in ChemBio3D and minimised by using MM2 force field. The energy for molecule 9 was straight away found from one minimisation and the value obtained was 54.17 kcalmol-1 (226.6 kJmol-1). This value did not change even when the positions of the atoms were moved slightly. When the atoms were distorted too much the energy obtained was higher than the value recorded and hence it can be concluded that the value obtained for molecule 9 was the lowest value. The molecular geometry of molecule 9 that corresponds to this geometry is shown on the left.


However, for molecule 10 the procedure was not as easy because initially the molecule drawn for 10 converted back to the geometry of molecule 9 when optimised and gave the same energy value as the optimised molecule 9. Therefore the carbonyl group had to be manually moved below the ring in the 3D structure of the molecule and then this was minimised, but the structure changed and the energy was very high 120.6 kcalmol-1 (504.6 kJmol-1). The carbonyl was moved below the plane of the ring again and re-optimised to give 65.55 kcalmol-1 (274.3 kJmol-1), but the carbonyl was planar in the molecule. The carbonyl group was again moved below the plane and some atoms in the ring were slightly moved and again the structure was optimised and the energy obtained was 44.32 kcalmol-1 (185.4 kJmol-1). The cyclohexane ring adopted the chair conformer in this final optimisation (see right).
The energy initially for molecule 10 was higher than the energy for molecule 9, but eventually the energy obtained for molecule 10 was lower than for molecule 9 and hence molecule 10 is the more stable intermediate and likely to form.
| Type of Energy kcalmol-1 | Molecule 9 | First Optimisation Molecule 10 | Second Optimisation Molecule 10 | Final Optimisation Molecule 10 |
|---|---|---|---|---|
| Stretch | 2.79 | 4.33 | 3.36 | 2.56 |
| Bend | 16.59 | 76.63 | 21.60 | 10.70 |
| Stretch-Bend | 0.46 | -0.03 | 0.71 | 0.33 |
| Torsion | 20.60 | 17.64 | 23.07 | 19.58 |
| Non-1,4 VDW | -0.44 | -0.42 | -0.20 | -1.20 |
| 1,4 VDW | 13.99 | 22.53 | 16.81 | 12.54 |
| Dipole/Dipole | 0.18 | -0.07 | 0.19 | -0.18 |
| Total Energy | 54.17 | 120.60 | 65.55 | 44.32 |
| Total Energy/ kJmol-1 | 226.65 | 504.59 | 274.26 | 185.43 |
The reason why molecule 9 is higher in energy than molecule 10 is not only due to the conformation of the cyclohexane ring (chair in 10 and twist boat in 9) but also due to the fact that the cyclohexane ring and cyclopentane ring both bend downwards in molecule 9 and hence the steric hindrance is increased.
In both molecules the major contributions to the total energy of each molecule is from the bend, torsion and 1,4 VDW components. This means that the bond angles and dihedral angles deviate from normality and the molecules are under strain. In both molecules the angle for the carbon double bond should be 120o, but it is actually 108o. In addition, the dihedral angle between the carbonyl oxygen and the hydrogen on the adjacent carbon in the ring is 20o in molecule 9 and 42o in molecule 10. The actual dihedral angle should be 60o and hence this deviation causes the molecules to be under strain.
The alkene in these intermediate molecules reacts very slowly compared to other alkenes. This is because the alkene in molecules 9 and 10 is a hyperstable olefin. This is where the olefin has a negative olefin strain energy, which means that the olefin has a lower energy and is more stable than its corresponding alkane and hence does not readily undergo hydrogenation. In order to promote hydrogenation of these types of alkenes the reaction conditions have to be changed in order to ensure that the alkene is not hindered.[4]
Regioselective Addition of Dichlorocarbene

The results below were recorded by using the MOPAC interface PM6 method. This is because MM2 does not look at the electronic aspect of reactions and how electrons affect bonds, whereas the MOPAC interface does and therefore a chemical reaction can be described in terms of molecular orbitals. We are moving away from treating the molecule with a classical mechanical method to a method which involves quantum mechanics and includes the wave description of electrons.
Using MM2 the total energy of molecule 12 was found to be 17.91 kcalmol-1 (74.96 kJmol-1). Once the molecule had been optimised the PM6 method was implemented in order to be able to obtain diagrams of the HOMO-1, HOMO, LUMO, LUMO+1, LUMO+2 (see below).
From the below diagrams of the MOs of molecule 12 it can be seen that in the HOMO most of the electron density is on the syn carbon double bond to the C-Cl bond and in the LUMO most of the electron density is on the anti carbon double bond. This therefore means that when molecule 12 reacts with an electrophile such as dichlorocarbene or peracid, the double bond that is likely to be attacked is the syn double bond as it is the most nucleophilic. This is because a lot of electron density of the HOMO is around the syn double bond and hence the syn double bond is electron rich and can donate these electrons to the empty p orbital in the dichlorocarbene and hence form a bond (react). A lot of electron density of the LUMO is around the anti double bond and hence this double bond is electron deficient and hence will not react very well with the dichlorocarbene.[5]
 |
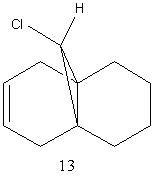 |
The same procedure was carried out on molecule 13, which is a hydrogenated version of molecule 12. The anti double bond has been hydrogenated to give molecule 13. The total energy of molecule 13 was found to be 22.35 kcalmol-1 (93.51 kJmol-1). The below pictures show the MOs of molecule 13. In the HOMO of molecule 13 there is not much electron density around the syn double bond and hence the syn double bond has become less nucleophilic.

| Molecule 12 | Molecule 13 | |
|---|---|---|
| Bond Stretch | Frequency / cm-1 | Frequency / cm-1 |
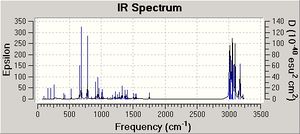
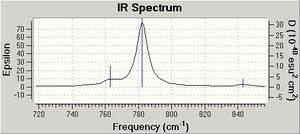
| C-Cl | 772.65 | 782.24 |
| Anti C=C | 1740.85 | - |
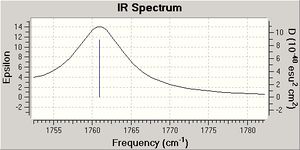
| Syn C=C | 1760.97 | 1757.32 |
| C-C | - | 1098.97 |
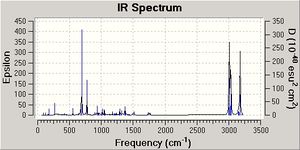
After the MM2 and MOPAC PM6 methods were carried out on molecules 12 and 13, a Gaussian input file was created and sent off to scan. The data generated from this procedure was used to produce a predicted IR spectrum for both molecules (see data above).
The data obtained conveys that the C-Cl bond in the dialkene (molecule 12) is weaker than the C-Cl bond in the monoalkene (molecule 13). This change in bond length is a direct result of the hydrogenation of the anti double bond of molecule 12 to form molecule 13. In molecule 12 the pi electrons of the anti carbon double bond interact with the antibonding sigma orbitals of the C-Cl bond (sigma star orbital) and hence weaken the C-Cl bond and make the IR frequency of the C-Cl bond smaller. In molecule 13 there is no anti carbon double bond and hence there are no pi electrons to donate to the sigma star orbital of the C-Cl bond and therefore the bond does not weaken and so the frequency of the C-Cl bond is higher.
In addition, the predicted IR spectrum for molecule 12 show C=C stretch frequencies, which is expected. The syn carbon double bond is stronger than the anti carbon double bond in molecule 12 as the syn double bond has a higher frequency and so this confirms the syn double bond in the dialkene is more nucleophilic and more likely to be attacked by electrophiles.
The intensity of the peaks in the IR spectra produced differ because the intensity depends on the change in polarisation. Therefore as the C-Cl bond is more polar than the C-C bond, the C-Cl bond frequency is more intense.
IR data was also found for other molecules where one hydrogen atom on the anti alkene in molecule 12 was replaced by an OH (molecule 14) or by a CN (molecule 15). The following data was obtained:
| Molecule 14 | Molecule 15 | |
|---|---|---|
| Bond Stretch | Frequency / cm-1 | Frequency / cm-1 |
| C-Cl | 766.79 | 765.79 |
| Anti C=C | 1776.59 | 1706.31 |
| Syn C=C | 1756.26 | 1756.54 |
| O-H | 3821.35 | - |
| CN | - | 2340.06 |
The results show that in both molecules the C-Cl bond has weakened compared the C-Cl bond in molecule 12. In molecule 14 the anti C=C has strengthened, but in molecule 15 the anti C=C double bond has weakened. The syn C=C bond is roughly the same strength in both molecules and compared with molecule 12. The reason for these observations is because the OH group in molecule 14 is slightly electron donating even though the O atom is very electronegative. The OH donates its lone pair of electrons into the anti C=C bond and hence strengthens the bond compared to molecule 12. As there is more electron density in the anti C=C bond in molecule 14, the electrons are more likely to donate into the sigma star orbital of the C-Cl bond and hence weaken it. In molecule 15 the CN group is electron withdrawing and hence the anti C=C bond is weakened as the electrons in the double bond are drawn to the CN group.
 |
 |
|---|---|
 |
 |
References
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
- ↑ S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0 10.1016/S0040-4039(00)92617-0
- ↑ Alan B. McEwen, Paul v. R. Schleyer, J. Am. Chem. Soc., 1986, 108 (14), pp 3951–3960 DOI:10.1021/ja00274a016
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447