Transition states and reactivity

Introduction

This experiment involves using computational quantum chemistry methods to analyse molecular structures, their molecular orbitals (MO's) and energetics. Providing information about reaction pathways, activation energies and transition state (TS) intermediates. The transition state structures that are investigated are based on the shape of the potential energy surface; these are found through computational molecular-orbital based methods by solving the Schrödinger equation. The computational methods used to optimise and run frequency calculations on molecular structures are the semi-empirical method PM6 and the Density Functional Theory (DFT) method B3LYP.

Computational methods used

The semi-empirical PM6 method is based on the Hartree–Fock (HF) formalism, in which the wavefunction of a system is expressed through the use of a linear combination of Slater determinants with fixed coefficients. The PM6 method differs with the HF method as it makes many approximations and obtains some parameters from empirical data. This method is used for molecules where the full HF method of optimisation without any approximations is too expensive. The fact that the PM6 method incorporates empirical data as approximations allows for optimisation to be fast as less calculations need to be made. However, these approximations mean that results are less accurate. On the other hand, the B3LYP method is a DFT-hybrid method which is based on electron density in antithesis to the PM6 which is based on wavefunctions. The B3LYP method, which incorporates both the HF and DFT methods, uses less approximations making it a more accurate but more computationally expensive optimisation method compared to the PM6 method.
Nf710 (talk) 10:19, 22 March 2018 (UTC) This is good you have clearly shown some understanding here and you are correct. However it would have been good to show some equations here to help back up your discussion.

The Potential Energy Surface of a system

The Potential Energy Surface (PES) describes the energy of a system in terms of parameters such as the positions of atoms in a structure. For a molecule with N_atoms there are 3N_atoms-6 independent geometric variables that are determined; including bond lengths, bond angles and torsional angles. Using computational methods the points of a potential energy curve can be determined and analysis of its first and second derivatives yields important information about the systems reaction energetics. The first derivatives give the gradient and the second derivatives give the curvature of the (PES). Points with zero gradient are minima which correspond to products, or can be saddle points, energy maxima, that represent transition state species. The transition state is an intermediate structure between reactants and products in the reaction pathway; it is a maximum in the potential energy curve that requires maximum energy to be overcome to result in products.

Nf710 (talk) 10:22, 22 March 2018 (UTC) IT is only a maximum in the reaction coordinate.

The PES curve's first derivative can be related to the force acting on atoms which acts in the direction that will lower potential energy, giving it a negative value. At bond length distances above the equilibrium bond length the potential energy curve gradient is positive and the force acting upon it to reach the minimum equilibrium length point on the curve is negative. At bond length distances below the equilibrium bond length the potential energy curve gradient is negative and the force acting on it to increase the bond length is positive^[1]. Since the TS is at the maxima the force acts on it in the direction to minimise bond length to reach products indicating it has a negative force constant. A TS can therefore be identified by an imaginary frequency in its first vibrational mode since calculating the frequency of a harmonic oscillator with a negative force constant yields an imaginary frequency. This frequency calculation was a method to confirm if a TS structure was created after optimisation.

Nf710 (talk) 10:22, 22 March 2018 (UTC) Technically the force constant comes from diagonalisation of the hessian matrix, which bring the coordingates into the basis of the normal modes which is a linear combination of the degrees of freedom. Hence when you move back an forth along this vector you ae changing them all at the same time. hence why it looks like a vibration.

The reactions that will be studied using these computational methods are pericyclic reactions which occur through a cyclic TS in a concerted fashion. More specifically Diels-Alder cycloadditions will be looked into where a [4+2] cycloaddition occurs to form a 6-membered ring system.

Exercise 1

(Fv611 (talk) Good job across the whole exercise. Well done!)

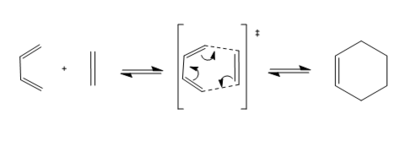
The transition state of the Diels-Alder reaction between butadiene and ethene, shown above in scheme 1, will be studied. This reaction involves a [4+2] cycloaddition between the two reactant molecules resulting in a ring product. The PM6 optimisation method was used in this exercise to optimise the reaction molecules.

Molecular orbital analysis

Optimising the reactants, transition state and product molecules revealed the energies and shape of the molecular orbitals for each structure. This then helped to identify the reactant HOMO and LUMO MO's that reacted to form the transition state, leading to the construction of the molecular orbital diagram for the transition state, figure 2.

Ethene MO's

Butadiene MO's

Transition state Mo's

Ethene-φ1 HOMO

Butadiene-φ2 HOMO

Transition state HOMO 1

Ethene-φ2 LUMO

Butadiene-φ3 LUMO

Transition state HOMO 2

Transition state LUMO 1

Transition state LUMO 2

The Jmols of the MO's of the reactants and TS have been displayed above. It is observed that for a molecular orbital to react successfully and produce a product they need to be of the same symmetry. In the MO diagram it can be seen that symmetric reacts with symmetric and anti-symmetric reacts with anti-symmetric orbitals to product a TS HOMO or LUMO of the same symmetry.If they are of different symmetry the reaction is disallowed. This is seen where the butadiene HOMO which is asymmetric reacts with the ethene LUMO, also asymmetric, to product TS HOMO 1 and LUMO 2 which are both asymmetric.

The overlap integral for a symmetric-antisymmetric interaction is zero, whereas for a symmetric-symmetric or antisymmetric-antisymmetric interaction a non-zero value is obtained. The transition state MO diagram reveals that the transition state orbitals produced arise from s-s or a-a interactions, these inteaction contain non-zero overlap integrals, yielding true MO's.

Carbon-Carbon bond length analysis

Table 1-Carbon-Carbon bond lengths of the reactants, TS and products.
Carbon bonds	Ethene bond lengths (Å)	Butadiene bond lengths (Å)	Transition state bond lengths (Å)	Cyclohexene bond lengths (Å)	Bond length change
C₁-C₂	1.327	-	1.380	1.538	Increase
C₂-C₃	-	-	2.115	1.536	Decrease
C₃-C₄	-	1.333	1.380	1.493	Increase
C₄-C₅	-	1.471	1.411	1.333	Decrease
C₅-C₆	-	1.333	1.380	1.493	Increase
C₆-C₁	-	-	2.114	1.536	Decrease

The typical length for a C-C sp³ bond is 1.54 Å, whereas the length of a C-C sp² bond is 1.34 Å ^[2]. In table 1 it can be seen that single and double bond values are approximately the same length as the typical values expected, confirming the structures obtained through optimisation. For example the bond between C₁-C₂ is seen to increase as the bond becomes sp³ hybridised from sp².
The Van der Waals radius of a carbon atom is 1.7 Å ^[3]. In the Diels-Alder transition state is can be seen that the bonds that form between C₆-C₁ and C₂-C₃, 2.1 Å, are shorter than two carbon Van der Waals radii values, 3.4 Å. This confirms that in the TS the molecules, that were far apart, gradually come closer; when they are found within less than two carbon Van der Waals radii they are able to approach the formation of a single bond that is found in the products.

Transition state vibration

The vibration that corresponds to the reaction path at the transition state is identified as the one with a negative frequency, known as the imaginary frequency stated above. The Diels-Alder transition state at this vibration is displayed below. It can be seen that at this transition state vibration the bonds between the two reactants form in a synchronous manner, this is seen by the movement of the displacement vectors that move towards each other at the same time. This synchronous bond formation is further confirmed by the analysis of the IRC that shows the reactions proceeds through a concerted mechanism. This is the typical mechanism pathway found for Diels-Alder cycloadditions.

Transition state vibration

The IRC for the Diels-Alder transition state can be found here
The .log file for the PM6 optimised cyclohexene TS can be found here
The .log file for the PM6 optimised cyclohexene product can be found here

Exercise 2

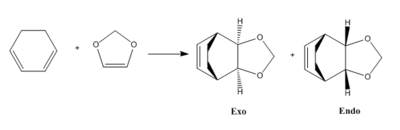
In this exercise the [4+2] cycloaddition reaction between cyclohexadiene and 1,3-dioxole is investigated. This Diels-Alder reaction yields two products, the exo and endo products, due to the different symmetries of the transition state.

Molecular orbital analysis

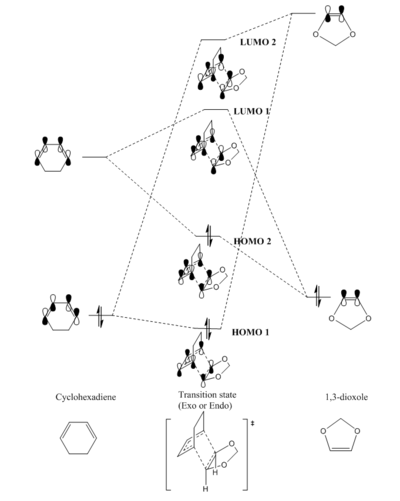
Using the B3LYP optimisation method the TS for both the exo and endo molecules was determined. This yielded the occupied, HOMO, and unoccupied, LUMO, orbitals and their energies for each TS. The HOMO and LUMO orbitals for both symmetries are displayed below. These were then used to construct an MO diagram for this Diels-Alder reaction, figure 3, which was based on the MO diagram of the butadiene and ethene TS as these reacting molecules are symmetrically similar.

EXO HOMO 1

EXO HOMO 2

EXO LUMO 1

EXO LUMO 2

ENDO HOMO 1

ENDO HOMO 2

ENDO LUMO 1

ENDO LUMO 2

(Fv611 (talk) The MO diagrams of endo and exo are different and you should have discussed the reasons why that might be. Addiyionally your MO diagram is missing symmetry labels.)

According to symmetry the cyclohexadiene and 1,3-dioxole MO's can be considered as the butadiene and ethene MO's from figure 2 respectively. The energy levels of the reactant and TS orbitals has been determined from their B3LYP/6-31G(d) optimised .chk file MO's, and have been positioned accordingly. It is observed that the energy level of these MO's is slightly shifted compared to the butadiene ethene MO's. The cyclohexadiene HOMO is lower in energy than the 1,3-dioxole HOMO, whereas, in figure 2, the butadiene HOMO is higher in energy compared to the ethene HOMO. It is to be noted that both the exo and endo TS have different geometries and their MO's differ slightly in energy, however,they both contain the same molecular orbital combinations and their MO's are found in similar energetic regions compared to reactant MO's, therefore, one molecular orbital diagram has been drawn for both.
The .log files for the B3LYP/6-31G(d) optimised molecules can be found here:Cyclohexadiene, 1,3-dioxole, Exo TS, Endo TS, Exo product, Endo product.

Nf710 (talk) 10:40, 22 March 2018 (UTC) You shouldnt comapre the MOs energies of things on different PESs because they experience different potentials and therefore it is meaningless to compare them

Normal and Inverse demand Diels-Alder reaction analysis

In a normal demand Diels-Alder reaction the HOMO of the electron rich diene reacts with the LUMO, π^* bond, of the electron deficient dienophile ( the substituted alkene). In a normal demand reaction the HOMO of the diene reacts with the LUMO of the dienophile to form the HOMO and LUMO of the TS, this is seen in the reaction between butadiene (diene) and ethene (dienophile), figure 2, which produces HOMO 2 and LUMO 1.
In an inverse demand reaction, an electron deficient diene's LUMO now reacts with an electron rich dienophile's HOMO. This occurs due to a switch in energies of the diene's and dienophile's orbitals which occurs when an electron withdrawing group is attached to the diene, lowering its HOMO, and/or an electron donating group is attached to the dienophile, raising its π orbital's energy making it's HOMO higher in energy. This leads to the dienophile HOMO being high enough in energy to react with the diene's LUMO. This case is seen in the reaction between cyclohexadiene and 1,3-dioxole, figure 3, in which the dienophile, 1,3-dioxole, has electron donating oxygen atoms attached to it, raising its HOMO and allowing the TS HOMO 2 and LUMO 1 to be reached in an inverse demand reaction.

Nf710 (talk) 10:43, 22 March 2018 (UTC) Nicely explained well done.

Nf710 (talk) 10:45, 22 March 2018 (UTC) However you have only explained this qualitatively and not quantitatively. you can do this by lookng at the energy of the reactant MOs on the same PES (first point on IRC).

Energy calculations=

The Sum of electronic and thermal Free Energies for each molecule has been taken from the B3LYP/6-31G(d) optimised .log files

Table 2-Molecule energies.
Molecule	Energy (Hatree)	Energy (kJ/mol)
Cyclohexadiene	-233.324374	-612593.1906
1,3-dioxole	-267.068642	-701188.773
Reactants combined	-500.393016	-1313781.964
Endo TS	-500.332146	-1313622.149
Exo TS	-500.329167	-1313614.328
Endo product	-500.418692	-1313849.376
Exo product	-500.417319	-1313845.771

Table 3-Endo and Exo reaction barriers and energies.
Reaction	Reaction barrier (kJ/mol)	Reaction energy (kJ/mol)
Endo	159.8142	-67.41234
Exo	167.63557	-63.80753

Table 2 gives energy values of reactants, TS's and products for both the exo and endo geometries. These energy values were used to obtain calculations of the reaction barriers, also known as the activation energies, and the reaction energies for the endo and exo reaction pathways, table 3. The reaction barrier is the maximum energy in the reaction pathway which needs to be overcome for a reaction to proceed to its product. The reaction barrier energy is calculated as the TS minus the reactants and is the energy value needed to reach the maximum in the potential energy surface of the system. Furthermore, the reaction energy is calculated as the reactant minus the products and is the energy obtained when the minimum of the potential energy surface is reached. The results of the energy barriers and energies shown that the endo product is both the kinetically and thermodynamically stable product. This is explained through secondary orbital interactions that occur in the endo product between the ring π bond and the oxygen p-orbitals displayed in figure 5.

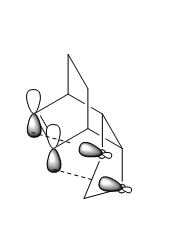
Figure 5:Endo product secondary orbital stabilisation interaction

These secondary orbital interactions stabilise the product, making the endo product the lowest energy product, the thermodynamic one. Additionally, through stabilising the product these secondary orbital interactions lower the energy barrier of the endo reaction making it the more kinetically stable one as well. The kinetic product has the lower energy barrier i.e less energy is needed to overcome its activation energy. Moreover, steric reasons that may affect the exo product, making it both thermodynamically and kinetically less stable, are the repulsive interactions that could occur between the bridgehead carbons of the ring and the 1,3-dioxole oxygens that are closer in the exo geometry. This could lead to destabilisation of the exo product molecule.

Nf710 (talk) 10:46, 22 March 2018 (UTC) Good section, but you could have gone into more detail in parts. But your energies were correct and you have come to the correct conclusions.

Exercise 3

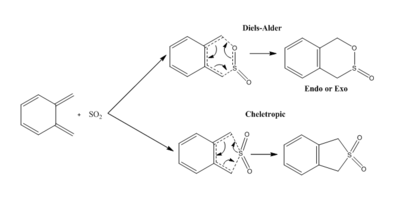
This exercise involves studying the Diels-Alder and Cheletropic reactions between o-Xylylene- and SO₂, dispayed in scheme 3.
The IRC for the three reaction pathways can be found here: Diels-Alder endo, Diels-Alder exo, Cheletropic.
The PM6 optimised .log files for the reaction molecules can be found here: o-Xylylene, SO₂, Endo TS, Exo TS, Cheletropic TS, Endo product, Exo product, Cheletropic product.

Energy calculations

The Sum of electronic and thermal Free Energies for each molecule has been taken from the PM6 optimised .log files.

Table 4-Molecule energies.
Molecule	Energy (Hatree)	Energy (kJ/mol)
ortho-Xylylene	0.177678	466.493625
SO₂	-0.119269	-313.1407834
Reactants	0.058409	153.352841
DA Endo TS	0.090560	237.765298
DA Exo TS	0.092077	241.748182
Cheletropic TS	0.099061	260.084675
DA Endo product	0.021705	56.9864818
DA Exo product	0.021454	56.3274813
Cheletropic Product	0.000005	0.013127501

Table 5-Reaction barriers and energies.
Reaction	Reaction barrier (kJ/mol)	Reaction energy (kJ/mol)
Endo	84.4124569	-96.3663593
Exo	88.3953407	-97.0253599
Cheletropic	106.731834	-153.339714

The most favourable route in this reaction is the endo route. As seen in table 5 the endo TS has the lowest reaction barrier energy, therefore, it is easier to overcome this reaction barrier to reach the TS and get a product. This lower energy barrier value is due to the endo TS and product having the secondary orbital interactions stated above; now between the oxygen p orbital and the pi orbitals of the conjugated benzene ring. These secondary orbital interactions stabilise the molecule, lowering its reaction energy barrier. It is to be noted that the cheletropic product is the more thermodynamically stable one but has a very high energy barrier which is unfavourable to reach as a lot of energy is needed to overcome it; this is an undesirable route. The endo product is the kinetically stable one and is the route that is preferred. A reaction profile diagram for the three pathways has been constructed in figure 6, enabling their energetics to be compared.

(You should show this secondary orbital overlap too Tam10 (talk) 13:35, 16 March 2018 (UTC))

Observing the IRC paths for the three reaction TS's, it can be seen that the xylylene 6-membered ring bonds change in length as the reaction proceeds from reactants to products through the TS. The xylylene ring obtains aromaticity as the bond length changes, this could be considered a driving force for the reaction and proves the molecule's instability as it readily rearranges as the reaction proceeds to the product.

An alternative reaction route

An alternative reaction route can occur in the Diels-Alder reaction between o-Xylylene and SO₂, where the SO₂ molecule reacts with the diene inside the six-membered ring of the xylylene molecule. This approach is displayed in scheme 4.

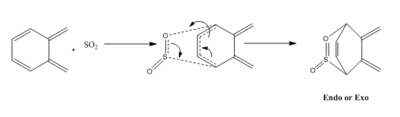
Table 6-Reaction barriers and energies.
Reaction	Energy barrier (kJ/mol)	Reaction energy (kJ/mol)
Endo	114.631969	-18.906229
Exo	122.469083	-23.353824

(The reaction energies are not negative by my calculations Tam10 (talk) 13:35, 16 March 2018 (UTC))

This endo and exo route are neither thermodynamically or kinetically stable since they have low reaction energy values (are not stable) and have high energy barriers. These high energy barriers require large amounts of energy to be overcome which is undesirable and would lead to products that are not very thermodynamically stable.
The IRC for the the alternative reaction pathways can be found here: Alternative Diels-Alder endo, Alternative Diels-Alder exo.

Further work

An electrocyclic reaction is a pericyclic reaction that involves a rearrangement of a pi to a sigma bond to form a ring product, such as the one displayed in scheme 5.

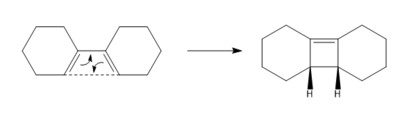
This reaction is photochemically allowed to occur in a 4π disrotatory mechanism according to the Woodward-Hoffmann rules. The molecular orbital interactions that yield the ring product are shown in figure 7. It can be seen that the orbitals move in a disrotatory fashion. The TS of the molecule was optimised to the PM6 level and the MO's where identified in order to confirm their movement.

(It's true that it would undergo disrotation under photochemical conditions, but you are running these calculations on the ground state ie thermal. Your IRC actually goes via conrotation (HOMO) if you observe it Tam10 (talk) 13:37, 16 March 2018 (UTC))

Even though the PM6 level of optimisation is not the most accurate for viewing the correct symmetry of the MO's; it is concluded through the MO's that this electrocyclic reaction proceeds with disrotatory motion, as the orbitals allign as expected in the TS LUMO of the molecule leading to the formation of the sigma bond. A higher level of optimisation would be more suitable to determine the direction of orbital movement.
The IRC for the TS can be found here.
The PM6 optimised .log files can be found here: Reactant, TS, Product.

Conclusion

Over the years computational chemistry has been and is still being widely developed. It provides the opportunity to optimise structures; revealing information about their bond lengths, bond angles, MO's and their energetics. These optimised structures can then be used for comparison to synthetically formed structures in the lab. Optimisation methods such as the PM6 and B3LYP methods have proven to yield accurate results for molecules and TS's that can be used to further analyse and compare the thermochemistry of reactions. A huge advantage of quantum computational chemistry is that it allows for the prediction and analysis of a TS that cannot be isolated as an individual structure in the physical world, as in the case of the pericyclic reactions that have been investigated in this experiment.

References

↑ Computational Quantum Chemistry. Chapter 1, 2013, Pages 1-62.
↑ B.P. Stoicheff. "The variation of carbon-carbon bond lengths with environment as determined by spectroscopic studies of simple polyatomic molecules". Tetrahedron, Vol 17, Issues 3–4, 1962, Pages 135-145.
↑ A Bondi. "Van der Waals Volumes and Radii". J. Phys. Chem., 68 (3), 1964, Pages 441–451.

[intro-1] Computational Quantum Chemistry. Chapter 1, 2013, Pages 1-62.

[C_length-2] B.P. Stoicheff. "The variation of carbon-carbon bond lengths with environment as determined by spectroscopic studies of simple polyatomic molecules". Tetrahedron, Vol 17, Issues 3–4, 1962, Pages 135-145.

[C_radius-3] A Bondi. "Van der Waals Volumes and Radii". J. Phys. Chem., 68 (3), 1964, Pages 441–451.

[1]

[2]

[3]