Rep:Mod:pk1615
Analysis of ammonia
Ammonia is the molecule that has been drawn and optimised using GaussView. The optimisation calculation had specific methods i.e B3LYP thus providing an approximation of the structure from information gained from the Shrodinger equation. The basis set of this calculation is 6-31G(d.p) which gives medium level accuracy.
General information about NH3
| Molecule | NH3 |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| RMS gradient | 0.00000485 a.u. |
| Point group | C3V |
| N-H bond length | 1.01798Å |
| H-N-H bond angle | 105.741° |
Optimised Ammonia Molecule
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
ammonia molecule |
The optimisation file is liked to here
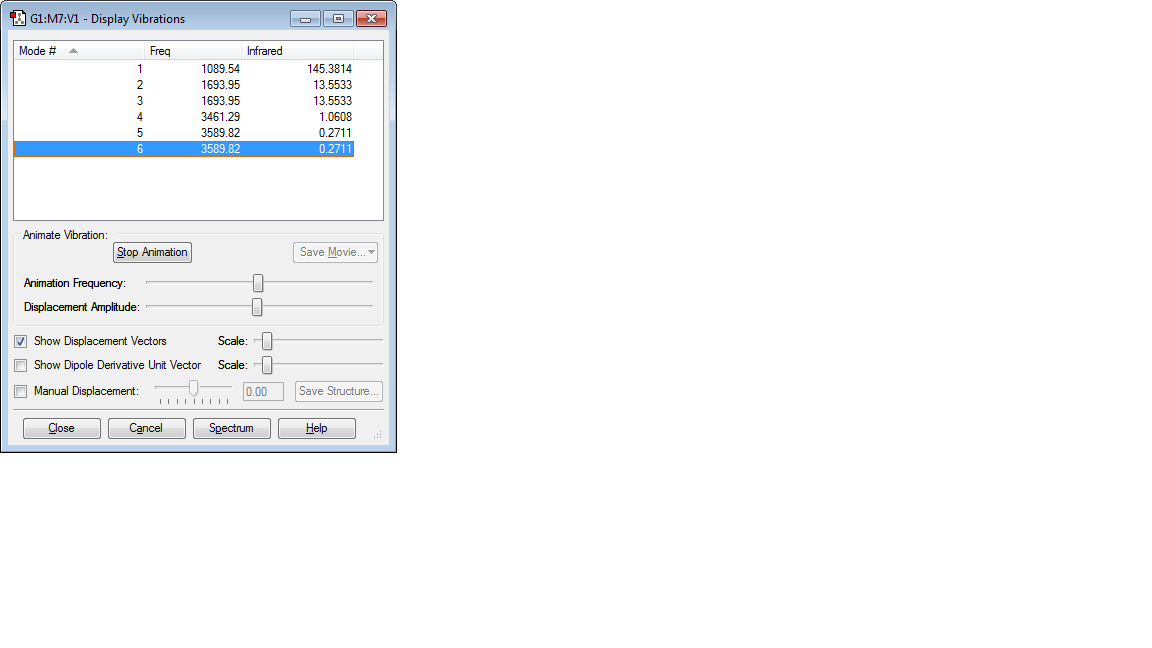
NH3 Vibrations
–6 modes are expected for the ammonia molecule from the 3N-6 rule. [3(4)-6]
–The following modes are degenerate:
2 and 3 5 and 6
–'Bending' vibrations: modes 1,2 and 3 –'Bond stretch' vibrations: modes 4,5, and 6
–The mode 4 is highly symmetric.
–Mode 1 is known as the 'umbrella' mode.
–You would expect 2 bands in an experimental spectrum of gaseous ammonia since symmetric stretching does not give rise to a peak in infrared spectroscopy (there is no change in dipole moment in symmetric stretching), therefore, mode 4 will not be visible in the spectrum. Also, degenerate modes appear as one band in an experimental spectrum, modes 2 and 3 will appear as one band. Modes 5 and 6 which are also degenerate are expected to appear as one band also but are not visible since their intensity is too low, a band is not visible.
Ammonia Charge Distributions
The charge on the nitrogen atom of ammonia is -1.125 and the charge of the hydrogen atom is 0.375. You would expect N to have a negative charge since it is more electronegative compared to H which would have a positive charge. The N attracts the electrons in the N-H bond towards itself as it is more electronegative, inducing a dipole charge.
Information about N2
| Molecule | N2 |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -109.52412868 a.u. |
| RMS gradient | 0.00000060 a.u. |
| Point group | D∞ |
| N-N bond length | 1.10550Å |
| N-N bond angle | Linear molecule |
Optimised Nitrogen Molecule
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
nitrogen molecule |
The optimisation file is liked to here
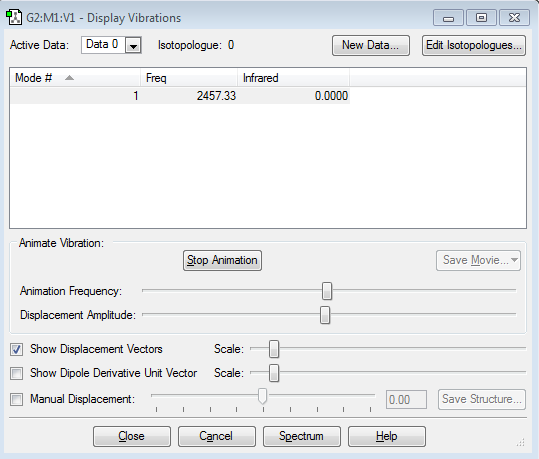
Nitrogen Vibrations
–There is one mode for the nitrogen molecule, which is proven by the 3N-5 rule for linear molecules.
–This mode is a stretching vibration which is highly symmetric. This indicates that nitrogen has no bands in an IR spectrum as it cannot change its dipole moment when vibrating, it will not absorb infra-red radiation.
General information about H2
| Molecule | H2 |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -1.17853936 a.u. |
| RMS gradient | 0.00000017 a.u. |
| Point group | D∞ |
| H-H bond length | 0.74279Å |
| H-H bond angle | Linear molecule |
Optimised Hydrogen Molecule
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
hydrogen molecule |
The optimisation file is liked to here
Hydrogen Vibrations
–3N-5 rule applies for linear molecules. Therefore, one mode is expected for the hydrogen molecule.
–The mode is a stretching vibration which is highly symmetric, therefore it does not appear as a band in IR for the same reasons as the nitrogen molecule.
Haber-Bosch process
Energies
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)=-3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
ΔE=(-0.0557907 a.u.)*2625.5 = -146.4784829 KJ/mol
It is apparent that the ammonium product is more stable compared to the gaseous reactants by -146.4784829 KJ/mol. This is indicated by the fact that the reaction is exothermic and it therefore favours lower temperatures. In exothermic reactions products have lower energies than reactants, they are more thermodynamically stable compared to reactants and have a more stable energy.
Comparison to literature value:
Literate value is -92.4 KJ/mol [1] which is lower energy released compared to our predicted energy value. The reason for this difference in value is the fact that we did not take into consideration any entropy factors. Entropy decreases in this reaction since four molecules of hydrogen and nitrogen are reduced to two molecules of ammonia.
Project Molecule: Silane
General Information about SiH4
| Molecule | SiH4 |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -291.88802685 a.u. |
| RMS gradient | 0.00000984 a.u. |
| Point group | Td |
| Si-H bond length | 1.48486Å |
| H-Si-H bond angle | 109.479° |
Optimised Silane Molecule
Item Value Threshold Converged? Maximum Force 0.000013 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000227 0.001800 YES RMS Displacement 0.000122 0.001200 YES
Silane molecule |
The optimisation file is liked to here
Silane Vibrations
–Using the 3N-6 rule you expect 9 modes for a silane molecule. [3(5)-6].
–Modes that are degenerate in energy inculde:
modes 2 and 3
modes 8 and 9
–'bending vibrations' are seen in modes 1-5.
'stretching vibrations are seen in modes 6-9.
–Mode 6 is a highly symmetric mode.
Charge analysis of SiH4
The charges of silicon and hydrogen in the silane molecule have been calculated and are shown below.
Silane is a molecule containing four Si-H bonds. Si is less electronegative compared to H which explains why Si has a positve charge and H has a negative charge. Whereas in methane the carbon holds the negative charge and the hydrogens have a positive charge, proving that SiH4 has reversed polarity compared to CH4. Silane's reversed polarity means that it can form complexes with transition metals more readily.
Molecular Orbitals
The image above is an image of a molecular SiH4 orbital, it is an molecular orbital that does not interact because it considers the 1s atomic orbital found in silicon that is too low in energy to react with the H 1s atomic orbitals ,therefore, no bonding is present. The 1s can be seen in the image as the very small red centre that is too small to react. It has the lowest energy compared to all the other molecular orbitals of silane at -66.12595 a.u. further proving that it is the 1s Si molecular orbital which is excepted to be the lowest in energy, this can be seen in SiH4 molecular orbital energy diagrams.
This is an image of the bonding molecular orbital that arises due to the interaction of the bonding Si 3s orbital and the fully bonding H4 fragment orbitals. This molecular orbital is fully occupied. The molecular orbital contributes to the bonding.
The SiH4 molecular orbital in the image above is due to the interaction of a bonding 3p atomic orbital in Si with the triply degenerate h4 fragment orbitals. It is a filled bonding molecular orbital and can be considered as one of the highest occupied molecular orbitals (HOMO).
The molecular orbital present is the anti-bonding molecular orbital that forms between a 3p Si orbital and the out-of-phase triply degenerate h4 fragment orbitals. It is the lowest unoccupied molecular orbital(LUMO). The energy of this molecular orbital is lower than the molecular orbital between the Si 3s and fully anti-bonding H4 fragment orbitals since it is less anti-bonding.
This is the anti-bonding molecular orbital between the Si 3s atomic orbital and the fully anti-bonding H4 fragment orbitals. It has a very high energy, 0.12285 a.u., as it this molecular orbital wants to be as anti-bonding as possible, therefore, is at a very high and unstable energy.